出租车资源优化配置的研究

谢　琛

(对外经济贸易大学保险学院，北京　100029)



出租车资源优化配置的研究

谢琛

(对外经济贸易大学保险学院，北京100029)

摘要：本文针对“打车难”这个社会问题，运用主成分分析的方法选取了合理的指标，建立了供给需求综合评估模型，并以天津市为例分析了其供求匹配程度。最后，通过打车费用的最优解设计缓解“打车难”的补贴方案。

关键词：主成分分析；供给需求回归模型；相关系数矩阵

一、问题的背景和重述

出租车是市民出行的重要交通工具之一，“打车难”是人们关注的一个社会热点问题。随着“互联网+”时代的到来，有多家公司依托移动互联网建立了打车软件服务平台，实现了乘客与出租车司机之间的信息互通，同时推出了多种出租车的补贴方案。

本文通过搜集相关数据，建立数学模型来解决以下几个问题：

(1)建立合理的指标，分析不同时空出租车资源的“供求匹配”程度；(2)分析“滴滴打车”和“快的打车”的出租车补贴方案是否对“缓解打车难”有帮助；(3)设计一个新的打车软件服务平台的补贴方案，并论证了合理性。

二、模型的建立

1.合理指标的选取

(1)初步分析相关指标

供给量即为出租车每年可提供的总服务次数(万次)，需求量即为出租车每年被需求提供服务的总次数(万次)。从供需关系来看，影响因素主要有：城市人口、城市经济发展水平(可以用衡量)、城市人口密度、城市交通发展状况(公交车站台数量)、旅游业发展水平(接待国际游客人次)、城镇居民可支配收入、私人汽车拥有数量、出租车每单的费用、出租车司机人均年收入、汽油价等因素有关。

(2)主成分分析法讨论

假设共有n个原始观测指标，分别为X1，X2，……，Xn，对n个指标进行线性组合，得到新的综合指标，即

Y=γ1X1+γ2X2…+γnXn

这n个指标不可能都对Y有很大的影响，故通过拟合优度来选取主成分。因为方差能反映变量自身的变化程度，原始指标的主成分可以根据方差来定义，由于Y=β′X，故有

Var(Y)=Var(β′x)=β′Var(X)β=β′∑β

因此，定义使得n个原始指标所有线性组合中方差最大的系数向量所对应的综合指标为第一主成分，以此类推，则数学模型为：

且Var(Y1)>Var(Y2)>…>Var(YR)，Cor(Yi,Yj)=0i,j=1,2,…,R;i≠j

上式反映了各成分的方差在总方差中的比重成依次递减的趋势，选择方差较大的主成分，以实现降维，简化系统结构的目的。

2.建立需求与供给的回归模型

(1)需求回归模型

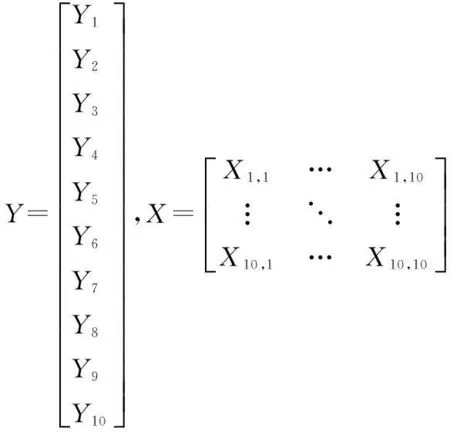
设需求回归模型为：

Y=X+μ

检验解释变量间是否存在多重共线性，用EViews检验出解释变量的相关系数矩阵如下：

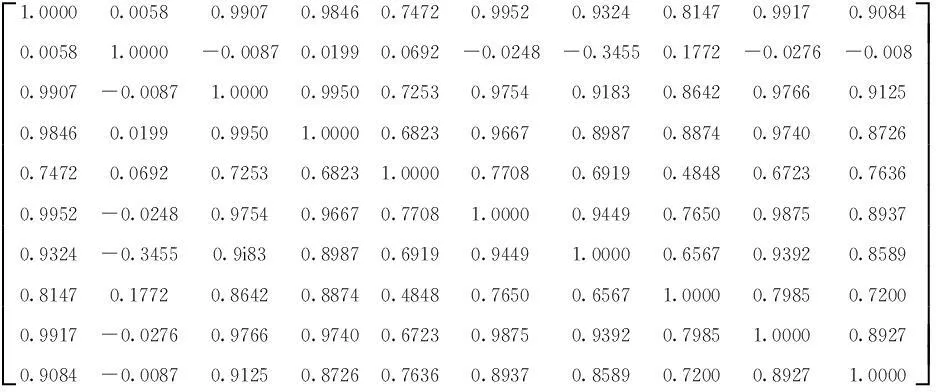
从两两变量间的相关性大小可以看出，lnX3与其它的变量间几乎都有较大的共线性。X3是GDP，与其它因素有较大的相关性会干扰整体模型，故剔除lnX3。

接来下选取对需求量有很大影响的指标。分别作lnY与lnX1，lnX2，lnX4，lnX5，lnX6，lnX7，lnX8，lnX9，lnX10间的回归，并得到各可决系数如下表所示：

表1　lnY与解释变量间的回归

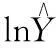
将其他解释变量分别导入上述初始回归模型，作逐步回归分析，寻找最佳回归方程。

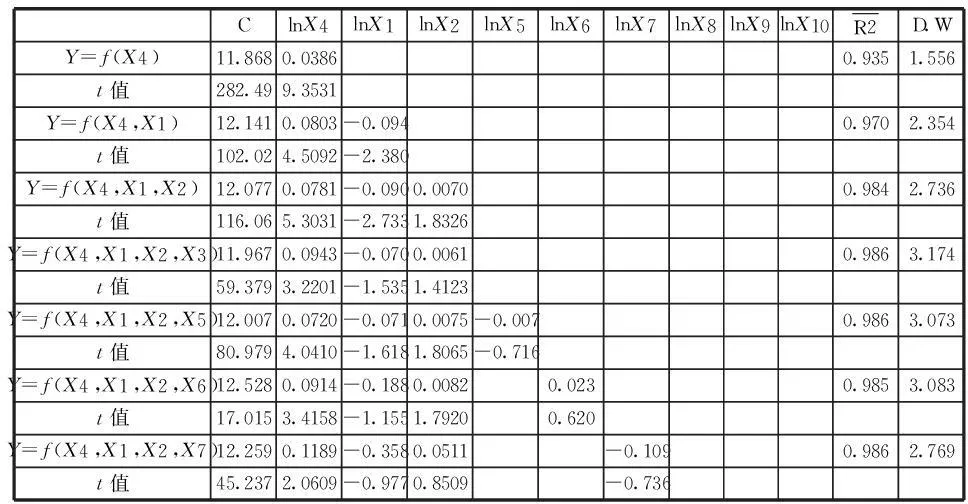
表2　需求模型的逐步回归分析表

在初始模型中引入X1，模型拟合优度提高，且参数符号合理。变量也通过了t检验，D.W.检验也表明不存在1阶序列相关性。引入X2，拟合优度再次提高，且参数符号合理，变量也通过了t检验和D.W.检验。引入X5，拟合优度提高，但X5的参数未通过t检验。引入X6，拟合优度提高，但X6的参数未能通过t检验。引入X7，拟合优度提高，但X7的参数未能通过t检验。引入X8，拟合优度提高，且X8的参数通过t检验与D.W.检验。引入X9，拟合优度再次提高，且X9的参数通过t检验与D.W.检验。引入X10，拟合优度虽然提高，但X10的参数未能通过t检验，且参数符号与实际经济意义不符。

以上分析表明，X5，X6，X7，X10是多余的。因此，出租车服务的需求函数应以φ=f(X1,X2,X4,X8,X9)表示为最优，拟合结果如下：

(2)供给回归模型

与需求回归模型步骤相类似，通过分析可得，对供给模型而言，Y5，Y6，Y7，Y9，10是多余的。因此，出租车服务的供给函数应以φ=f(X1,X2,X4,X8)表示为最优，拟合结果如下：

综上，所选取的合理指标应为：城市人口数量(万人)、城镇人口密度(人/万平方公里)、城镇居民可支配收入(元)以及人均每天在出租车上的花费(元)。

由于需求回归函数中，lnX9(出租司机年收入/人)对需求量的影响是不大的，只对供给量造成影响，且系数很小，为0.009977，因此在供求差量模型中，我们可以忽略它所带来的影响。供求差量方程如下：

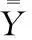
供求差量关于X1，X2，X4，X8的函数关系如下：

将城市人口数量与城镇居民可支配收入合并得：

3.供求匹配综合评价模型的建立与出租车资源供求匹配程度分析

(1)建立供求匹配综合评价模型

以实际空驶率与最优空驶率的偏差程度来衡量出租车的供求匹配程度。一般认为城市出租车空驶率大于30%小于40%的车辆数量是合理的(陆健，2003)，则在这个范围内，供求匹配程度是较高的。

空驶率的计算公式(卢杰，2012)为：

Lv=W1+W2

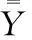
(2)以天津市为例分析出租车资源供求匹配程度

供求差量随年份的变化图如下：

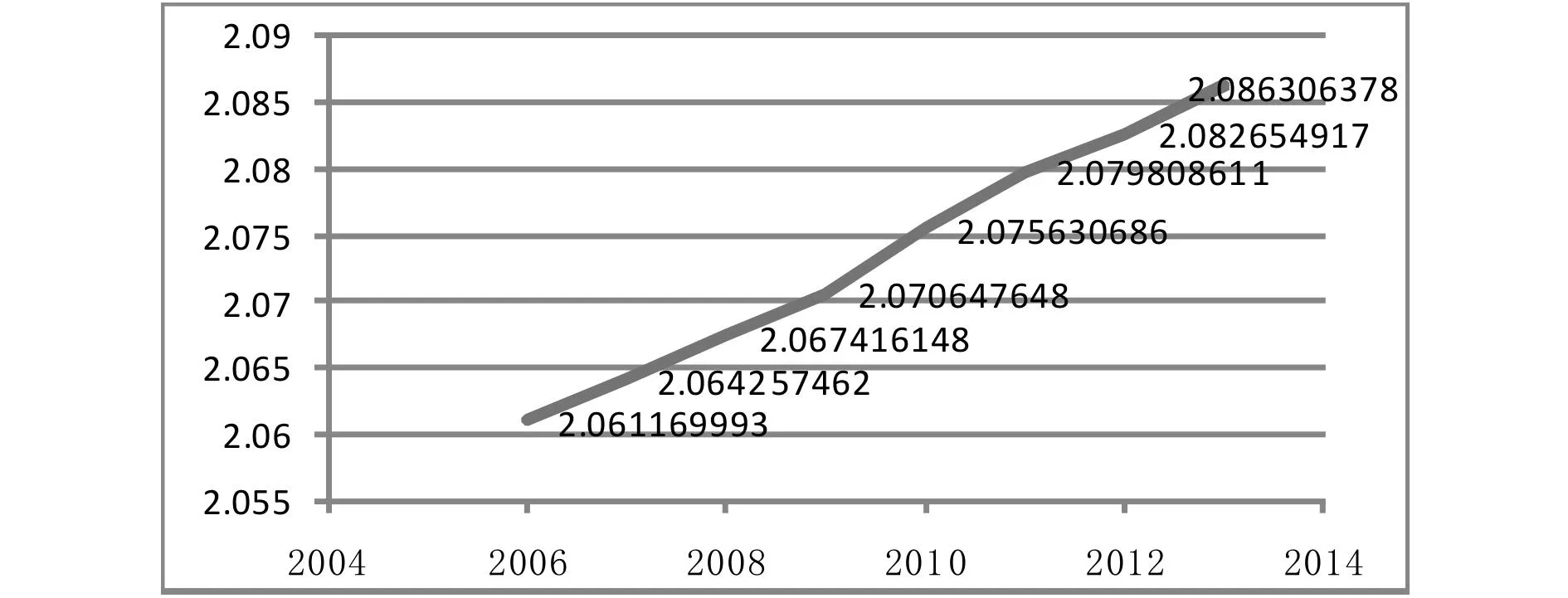
图1　供求差量随年份的变化(天津市)

由于供求差量随年份是呈逐年递增的状态，根据供求差量预测空驶率如下表所示：

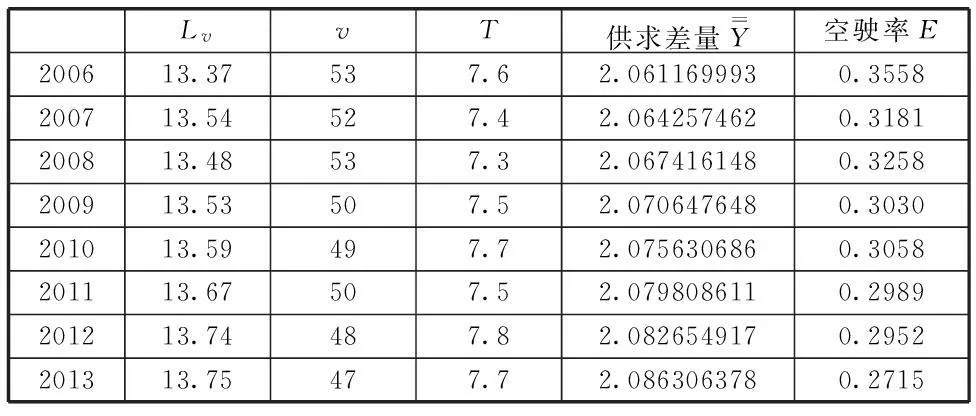
表3

天津市空驶率随年份的变化如下：

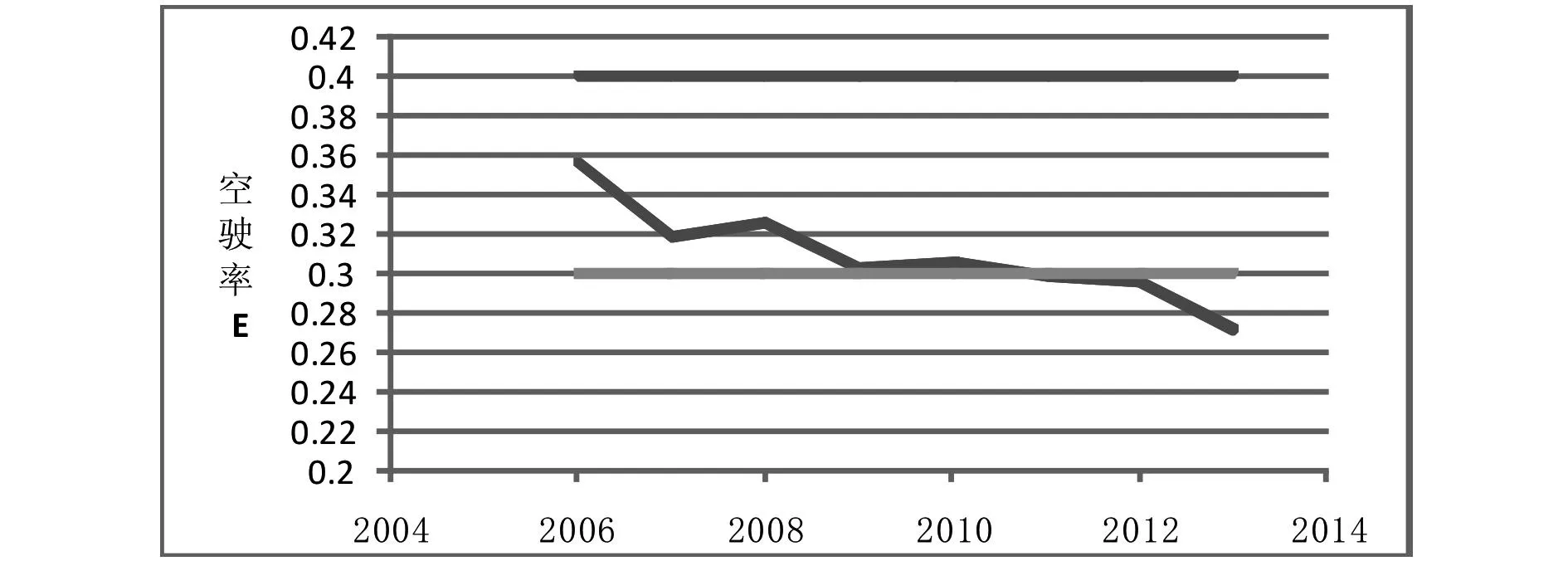
图2　天津市空驶率随年份的变化

从图中可以看出天津市的空驶率是逐年下降的，这说明天津市对出租车的供求差量程度是逐年上升的。

用实际空驶率与最优空驶率的偏差来评价“供求匹配”程度，所得结果如下表所示：

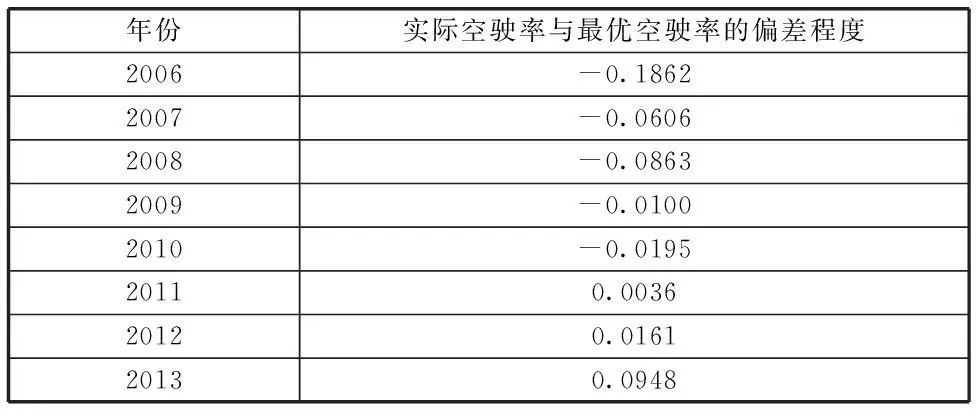
表4　实际空驶率与最优空驶率的偏差程度(天津市)

实际空驶率与最优空驶率的偏差程度随年份的变化如下图所示：

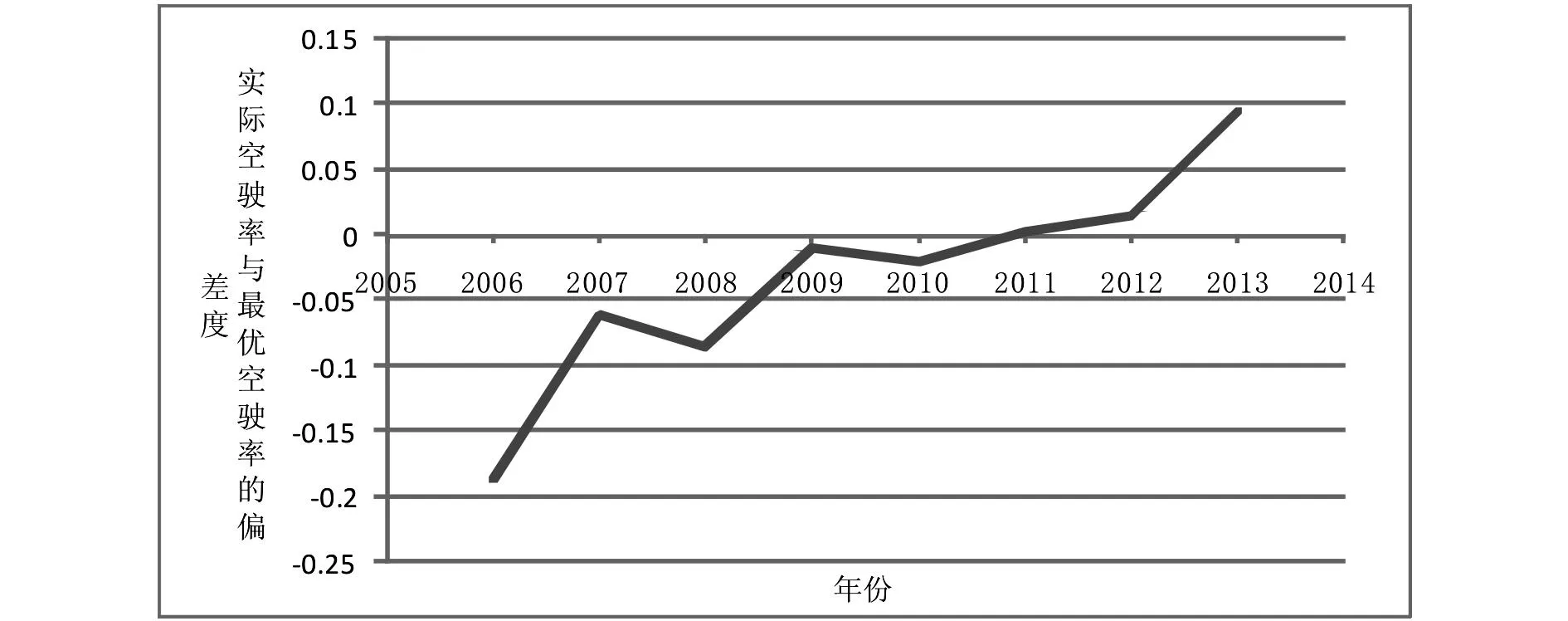
图3　实际空驶率与最优空驶率的偏差度

从图中可以看出，实际空驶率与最优空驶率的偏差程度随年份是呈递增的状态。

三、缓解“打车难”的补贴方案建议

从以上结论可以看出，若补贴过低，则会使得出租车司机实际所得到的金钱达不到所期望的收入，很有可能发生拒载现象；若补贴过高，则会有更多的人进入出租车司机行业，导致出租车的空驶率增加，会发生供过于求的现象。由此可见，对于天津而言，给予出租车司机的补贴为12.65元为最佳。

当平均每单给予出租车司机12.65元补贴时，补贴与每单向乘客收取的费用之和刚好满足出租车司机对平均每单行程费用的预期，而又不会因补贴过高使平均每单收入超过出租车司机的预期，导致他们“饥不择食”，盲目载客。这时出租车司机的欲载客程度恰好在“供求平衡”的水平上，可以使司机、乘客的匹配程度得到最好的满足。由此可见，当补贴偏离均衡水平，即偏离12.65元时，必然会出现司机的预期无法实现，或乘客不足以满足出租车司机的需求导致供求不匹配现象的出现。所以，将补贴控制在12.65元是最合理的补贴方案。

参考文献：

[1]李子奈，潘文卿.计量经济学[M].北京：高等教育出版社， 2013.

[2]卢杰.城市出租车需求量预测与数量规制[D].大连：东北财经大学， 2012.

[3]陆健，王炜.城市出租车拥有量确定方法[J].交通运输工程学报，2004，4(1).

[4]张珍珍.打车难缘由解析[J].今日中国论坛， 2012，(6)：36-38.

[5]本文数据来源中国统计网http：//www.itongji.cn/cms/article/index.