相关性分析——一个计量经济学的视角

罗　凯　吴　莹

(广州大学松田学院，广东　广州　511370)



相关性分析
——一个计量经济学的视角

罗凯吴莹

(广州大学松田学院，广东广州511370)

摘要：本文从概率论的两个例子出发构造了两组数据，通过分析得到了决定样本相关系数大小的一个因素——解释变量的取值分布是否对称，解释了计量经济学中相关性的含义，并给出了一个不相关但不独立的例子。

关键词：相关性；独立；对称

1.引言

在计量经济学中，相关性是一个很重要的概念，在一般的线性回归模型中，解释变量与被解释变量呈现出的便是一种相关关系。计量软件一般不会直接给出度量相关性的统计量，但会给出一个与之联系甚为紧密的结果——可决系数。虽然在计量经济学中，相关系数与可决系数所表示的含义大相径庭，但两者的联系如此紧密，以至于我们乍看时会有些许惊讶。具体一点说，如果我们用r表示相关系数，那么可决系数则为r2，用计量经济学的语言：

所以我们可以用可决系数的大小来分析相关系数的某些特征，但在此之前，我们先引入两个具体的例子。

2.两个例子

例1.设X～U(-1,1)，即X服从区间(-1,1)上的均匀分布，则其密度函数为：

因此：

再令Y=X2，则：

Cov(X,Y)=E(XY)-E(X)E(Y)

=E(X·X2)-E(X)E(X2)

=E(X3)-E(X)E(X2)

=0

显然，这里X与Y不相关。

例2.假设X～U(0，1)，即X服从区间(0，1)上的均匀分布，则其密度函数为：

因此：

再令Y=X2，则：

显然，这里X与Y并非不相关。

下面我们将应用这两个例子。

3.应用

利用上面的结论我们可以相应地构造出两组数据：

X0.40.30.20.100.10.20.30.4Y0.160.090.040.0100.010.040.090.16

X00.10.20.30.40.50.60.70.8Y00.010.040.090.160.250.360.490.64

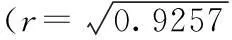
另外，我们还得到了一个不相关但却不独立的例子。很明显，第一组数据不独立，但它们却是不相关的。我们还可以严格地证明这一点，也就是说，对于例1，我们可以证明：

P(X

其实我们可以求出随机变量X的分布函数为：

随机变量Y的分布函数为

所以：

P(X

而随机向量(X，Y)的联合分布函数为：

从而P(X

至此，我们证明了我们的结论：两个变量不相关并不意味着独立。

参考文献：

[1]Damodar N.Gujarati， 2003.Basic Econometrics[M].4th ed.NewYork：McGraw-Hill Company.

[2]茆诗松，程依明，濮晓龙.2011.概率论与数理统计教程[M].第二版.北京：高等教育出版社.

[3]严士健，王隽骧，刘秀芳.2009.概率论基础[M].第二版.北京：科学出版社.