二维非线性非局域PT对称光晶格中的孤子

陈顺芳，成乐涛，金　刚

(1.湖北科技学院　电子与信息工程学院,湖北　咸宁　437100;2.通山一中,湖北　通山　437600 3.通城二中，湖北　通城　437400)



二维非线性非局域PT对称光晶格中的孤子

陈顺芳1，成乐涛2，金刚3

(1.湖北科技学院电子与信息工程学院,湖北咸宁437100;2.通山一中,湖北通山437600 3.通城二中，湖北通城437400)

摘要：本文研究了非局域非线性(2+1)维PT对称光晶格势中孤子的传输特性。首先，使用改进的平方算符法得到孤子数值解，然后用傅里叶配点法得到了孤子的稳定性情况，对于孤子在介质中传输的稳定性情况我们采用分布傅里叶算法得到了它的传播情况。分析了线性和非线性情况下光束的不同传播行为。研究发现在非局域非线性(2+1)维PT对称光晶格势中，孤子是否存在与它的传播常数，调制深度有着密切的关系，孤子的强度会随着传播常数的增大而增加，稳定性却随之减弱。当光功率超过一定值时孤子不能稳定传输。

关键词：非局域非线性；改进的平方算符法；带隙孤子；分步傅里叶算法

孤子又叫孤立子，它是一种特殊的超短脉冲，孤立波是一种在传播过程中保持形状、速度、幅度不变的脉冲状行波[1]。鉴于孤子具有的这些特性，孤子系统在现实世界有着广泛的应用潜力[2]。因此，孤子的形成及其传输特性的研究在目前是一个十分诱人的课题。

近年来, 非局域非线性介质中的空间孤子一直是研究的热点,人们对它们的各种独特的性质例如相互作用、稳定性进行了大量研究[3-6]。介质中非局域亮孤子间的相互作用取决于它们间的相位差、相干程度、材料的非线性非局域程度; 非局域基态和二阶体亮孤子总是稳定的, 而高阶亮孤子是震荡不稳的, 但如果样品的宽度超过一临界值, 三阶、四阶体亮孤子在其存在区域也总是稳定的。 非局域表面亮孤子的稳定性与体亮孤子的稳定性相似：基态和二阶表面亮孤子总是稳定的，高阶表面亮孤子是震荡不稳的。非局域基态界面亮孤子总是稳定的, 二阶及以上高阶界面亮孤子是震荡不稳的[7～9]。 与非局域亮孤子相比，由于其边界的特殊性，对非局域暗孤子相互作用及其稳定性的研究甚少。非局域暗孤子间的相互作用取决于孤子间距离以及介质的非局域程度，并存在着一个相互作用的临界点。 2+1维非局域暗孤子由于横向不稳定性容易分裂并演变成涡旋孤子，其暗孤子的稳定性如何, 目前还没有文章对其进行过具体研究.

本文基于二维非局域非线性薛定谔方程, 在前期研究[10～22]的基础上，通过数值模拟得到非局域暗孤子解, 然后提出了暗孤子稳定性分析理论, 并对其数值求解得到了非局域暗孤子的稳定性分析图, 最后利用加噪声的传输验证了稳定性分析理论的正确。

一、理论模型

非局域非线性介质中的近轴光束的传输特性，沿z轴传播的光束满足归一化的(2+1)维非局域非线性薛定谔方程[23]

(1)

其中u为无量纲光场包络波，z轴为光束传播轴，x轴和y轴为垂直于传播轴的光束展宽方向。V(x,y)和W(x,y)分别为PT对称晶格势的实部和虚部，T表示调制深度。μ∫-∞+∞g(x-λ)g(y-λ)|u(λ)2|dλ表示非局域的形式，PT对称晶格势为

V(x,y)=(sech2(x)+sech2(y))(cos(2x)+cos(2y))，

(2a)

W(x,y)=W0(tanh(2x)tanh(2y))(cos(2x)+cos(2y)),

(2b)

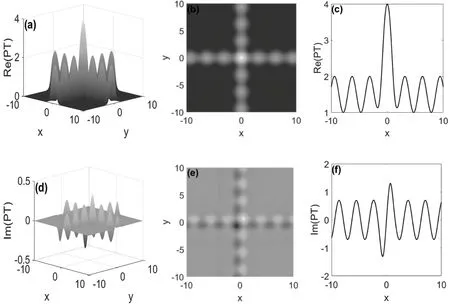
图1　PT势的强度分布 (a)(b)(c)偶对称V；(d)(e)(f)奇对称W

假设方程(1)中孤子解的形式为u=f(x·y)eibz，其中b为传播常数，模f(x,y)满足下列方程

uxx+ivxx+uyy+ivyy+T(uv+ivw+ivv-vw)+(u+iv) ∫-∞+∞g(x-λ)g(y-λ)|u2+v2|dλ=b(u+iv),

(3)

我们用改进的平方算符方法对方程(3)进行数值求解，得到PT孤子模。为了研究所得孤子的稳定性，我们对方程(1)采用微扰解:

U=eiμz{f(x,y)+[g(x,y)-h(x,y)]eλz+[g(x,y)+h(x,y)]*eλ*z}

(4)

其中g(x,y),h(x,y)≪f(x,y)为微扰项。将微扰后的U(x,y,z)代入方程(1)，然后对g(x,y)和h(x,y)进行线性化，得到它们的本征值方程:

uxx+ivxx+uyy+ivyy+T(uv+ivw+ivv-vw)+ξu3+ξiu2v+ξuv2+ξiv3=bu+ibv

(5)

令∫-∞+∞g(x-λ)g(y-λ)dλ=ξ则:实部：uxx+uyy+T(uv-vw)+ξu3+ξuv2=bu,虚部：vxx+vyy+T(vw+vv)+ξu2v+ξv3=bv.此本征值问题可以改写为

(6)

其中

A1=uxxuyy+Tv+3ξu2+ξv2-b,A2=-Tw+2ξuv,B1=Tw+2ξuv,B2=vxx+vyy+Tv+3ξv2+ξu2-b,此本征值问题可以通过傅里叶配点法进行求解，若本征值的实部为零，则孤子线性稳定，反之，线性不稳定。

为了便于讨论，取PT势的虚部强度W0=0.1。PT势的分布如图1所示，可以看到其实部V 关于原点偶对称，虚部W关于原点奇对称。

二、孤子的形成与分布

首先对方程(1)进行求解得到基模孤子，由图可以看出功率P随着传播常数μ的增加而增加，随着调制深度参数T的增加P减小。孤子在光晶格传输有一个存在的区域与稳定的区域，且随着T的增大，μ1和μ2均增加。孤子的能量为P=∫-∞+∞∫-∞+∞|f(x,y)|2dxdy。图2(a)(b)(c)表示不同调制深度T和传播常数μ时基极孤子的强度分布。图2(d)(e)(f)是对应孤子实部与与虚部的光场分布，图2(g)(h)(i)是对应孤子的稳定性光谱，我们在计算仿真过程中发现第一带隙结构中的基模孤子可以保持稳定，通过线性稳定性分析我们得到了三组孤子的稳定性光谱，由于仅仅包含虚部本征值，因此这个孤子是稳定的。

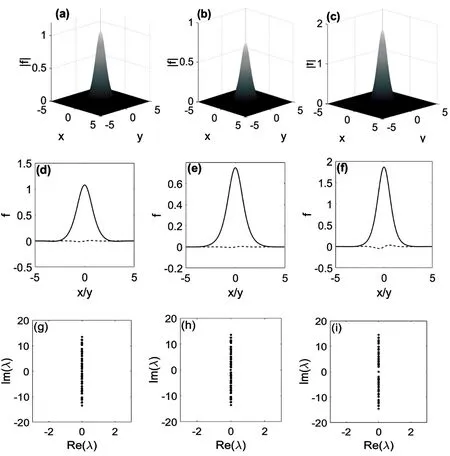
图2(a)(b)(c) 基模孤子强度分布图，参数为(a)T = 3，μ= 6.4，(b) T = 3，μ= 8.6，(c) T =6，μ= 8.6，(d)(e)(f)基模孤子光场分布(实部是实线，虚部是虚线)；(g)(h)(i) 基模孤子线性稳定性光谱

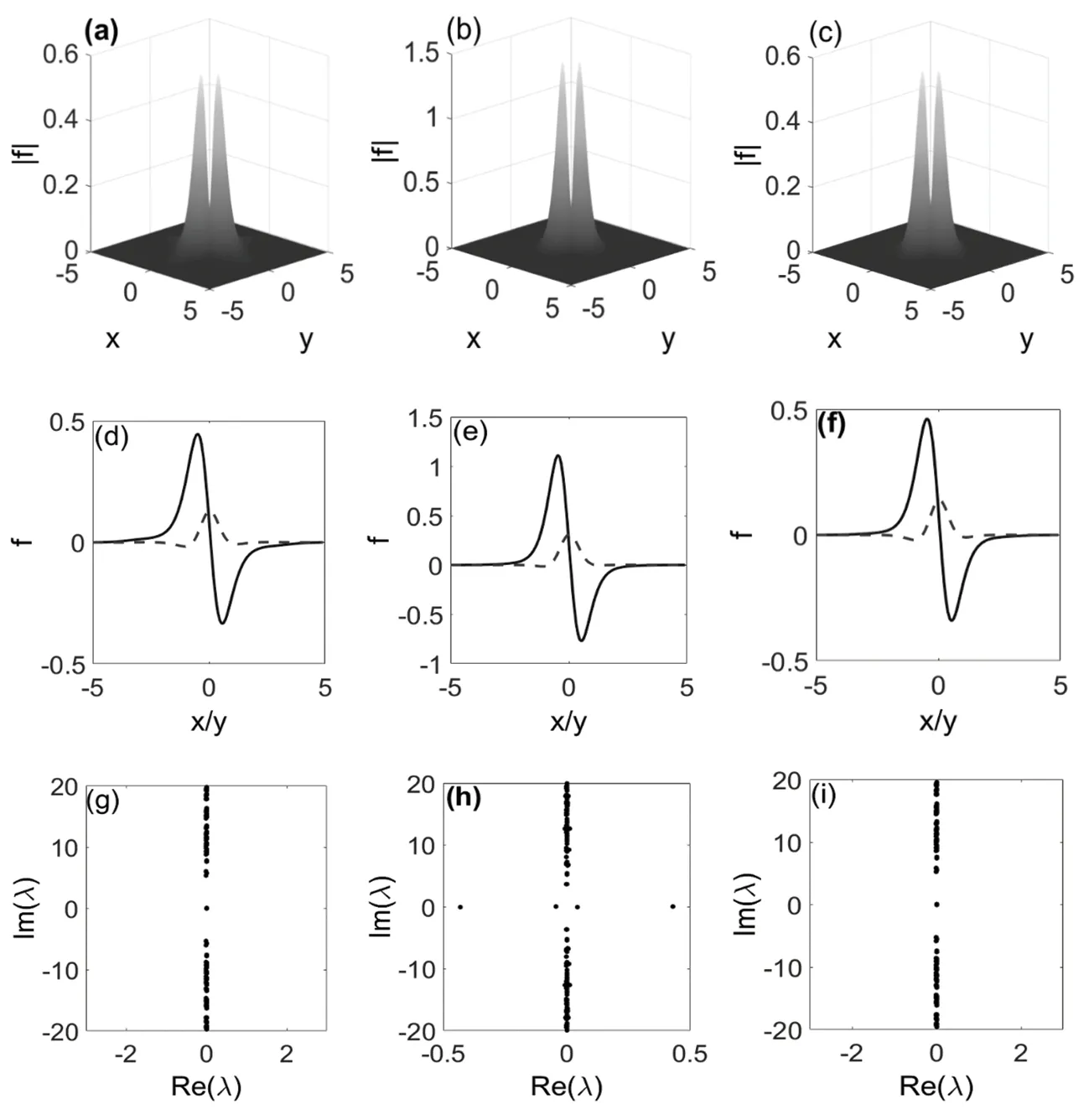
图3　(a)(b)(c) 偶孤子强度分布图，参数为(a)T = 5，μ= 8.4，(b) T = 5，μ= 9.6，(c) T =7，μ= 9.6，(d)(e)(f)偶孤子光场分布(实部是实线，虚部是虚线)；(g)(h)(i) 偶孤子线性稳定性光谱

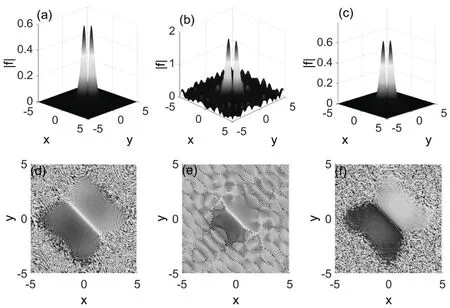
图4　(a)(b)(c)是偶孤子对应图3 (a)(b)(c)在z=400的输出；(d)(e)(f)是偶孤子在z=400的输出时刻的相位分布。参数为(a)T = 5，μ= 8.4，(b) T = 5，μ= 9.6，(c) T =7，μ= 9.6。

图3(a)(b)(c)表示不同调制深度T和传播常数μ时偶孤子的光场分布，当T=5，传播常数μ增加时，图3(b)中孤子的光强大于3(a)；当μ=9.6时，图3(c)中孤子的光强小于3(b)。图3.3(d)(e)(f)时对应的偶孤子的光场实部虚部分布图，可以看出它是实部关于原点偶对称，虚部关于原点奇对称。图3.3(g)(h)(i)是对应孤子的线性稳定性光谱，可以看出(g)(i)都是稳定的，(h)是不稳定的。这是由于方程(1)中的非线性项与非局域度之间的相互作用，非线性效应加强光束宽度变小抑制了孤子的能量转移，使得在这种平衡状态下得到稳定孤子。偶孤子之间存在着相互排斥的作用，所以在得到稳定的二极孤子时需要对基极孤子更大的调制深度，进而分裂得到偶孤子。 P随μ的增大而增大，其中，调制深度T增大，功率P随μ的增加而增加的速率变慢。随着T的增加P减小，其中，传播常数μ增大。

接着我们用分布傅里叶算法得到了偶孤子的传输图像。图4 (a)(b)(c)和(d)(e)(f)分别为偶孤子在Z=400时的输出图像和相位分布。由图4(a)(c)可见经过较长距离的传输后偶孤子能够在吸收微扰白噪声能量后保持其原有波形，从而传输稳定。而由图4 (b)我们可以看到孤子在经过较长距离的传输后发生了失真，波形严重变形，这是由于发生能量转移，使得孤子不稳定。从而证明了线性稳定性分析的结果。

三、结论

通过研究我们得出带隙基模孤子的功率P随着传播常数μ的增加而增加，随着调制深度参数T的增加功率P减小。孤子在光晶格传输有一个存在的区域与稳定的区域，且随着T的增大，μ1和μ2均增加。我们发现在第一带隙结构中的基模孤子可以保持稳定，通过线性稳定性分析我们得到了三组孤子是稳定的，而偶孤子之间存在着相互排斥的作用，所以在得到稳定的二极孤子时需要对基极孤子更大的调制深度，进而分裂得到偶孤子。功率P随传播常数μ的增大而增大，调制深度T增大，功率P随μ的增加而增加的速率变慢。随着T的增加P减小，传播常数μ增大。

参考文献：

[1]黄景宁，徐济仲，熊吟涛．孤子：概念、原理和应用[M]．北京：高等教育出版社，2004.

[2] 何影记．空间孤子传输的研究[D]．激光与光谱学研究所光电材料与技术国家重点实验室,2007.

[3]SiliuXu,MilivojR.Belic,Three-dimensionalHermite-Besselsolitonsinstronglynonlocalmediawithvariablepotentialcoefficients,OpticsCommunications,2014,313(15):62～68.

[4]A.Guo,G.J.Salamo,D.Duchesne,R.Morandotti.et,al.,ObservationofPT-SymmetryBreakinginComplexOpticalPotentials[J].Phys.Rev.Lett.2009,(103): 093902-093905.

[5]M.C.Zheng,D.N.Christodoulides,R.Fleischmann,andT.Kottos,PTopticallatticesanduniversalityinbeamdynamics[J].Phys.Rev.A2010,(82):010103～010109.

[6]SiliuXu,JiangchuLiangandLinYi,SpatialSolitonSolutionsinaHarmonicPotential[J].CHIN.PHYS.LETT.,2009, (26): 074215-0742219.

[7]SiliuXu,JiangchuLiangandZhongmingLi,Self-similarspatiotemporalsolitarywavesinBesselHermiteopticallattices[J].Chin.Phys.B,2011,20,11～17.

[8] 徐四六,刘会平, 易林, 强非局域非线性介质中的二维库墨-高斯孤子簇[J].物理学报, 2010,59(2):1069.

[9]高星辉, 张承云, 唐冬,等. 非局域暗孤子及其稳定性分析[J]. 物理学报, 2013, 63(4):228～232.

[10]SiliuXu,JiangchuLiangandLinYi,Self-similarsolitarywavesinBesselopticallattices[J].J.Opt.Soc.Am.B,2010, 27(1):99～106.

[11]SiliuXu,JiangchuLiangandLinYi,ExactsolitonsolutionstoageneralizednonlinearSchrodingerequation[J].Commun.Theo.Phys.,2010,(531):59～66.

[12]SiliuXu,MilivojR.Belic,andWei-PingZhong,Three-dimensionalspatio-temporalvectorsolitarywavesincouplednonlinearSchrodingerequationswithvariablecoefficients[J].J.Opt.Soc.Am.B,2013, 30(1):113～122.

[13]SiLiuXu,NikolaZ.Petrovic,MilivojR.Beliĉ,Vortexsolitonsinthe(2+1)-dimensionalnonlinearSchrodingerequationwithvariablediffractionandnonlinearitycoefficients[J].Phys.Scr.2013, (87):045401～045407.

[14]SiliuXu,MilivojR.Belic,Three-dimensionalHermite-Besselsolitonsinstronglynonlocalmediawithvariablepotentialcoefficients[J],OpticsCommunications,2014,313(15), 62～69.

[15]SiliuXuandMilivojR.Belic,LightbulletsinspatiallymodulatedLaguerre-Gaussopticallattices[J].J.Opt.Soc.Am.B,2013, 30 (10): 2715～2721.

[16]SiliuXu,MilivojR.Belic,Lightbulletsinthree-dimensionalcomplexGinzburg-LandauequationwithspatiallymodulatedKummer-Gaussopticallattice，EPL,2014, (108):34001～34007.

[17]Z.Lin,H.Ramezani,T.Eichelkraut,T.Kottos,H.Cao,andD.N.hristodoulides[J].Phys.Rev.Lett.2011,(106):213901～213904.

[18]S.L.Xu,M.R.Belic,LightbulletsincouplednonlinearSchrodingerequationwithspatiallymodulatedcoefficientsandBessel,trappingpotential[J].J.Mod.Opt.2015,(62):683～692.

[19]S.L.Xu,N.Petrovic,M.R.Belic,Exactsolutionsofthe(2+1)-dimensionalquinticnonlinearSchrodingerequationwithvariablecoefficients,NonlinearDyn.2015, (80):583～589.

[20]S.L.Xu,G.P.Zhou,N.Z.Petrovic,andM.R.Belic,NonautonomousvectormatterwavesintwocomponentBose-Einsteincondensateswithcombinedtime-dependentharmonic-latticepotential[J].J.Opt.17,2015.105605～105611.

[21]H.Ramezani,T.Kottos,R.El-Ganainy,andD.N.Christodoulides,UnidirectionalNonlinearPT-symmetricOpticalStructures[J].Phys.Rev.A,2010, (82)：043803～043809.

[22]Si-LiuXu,Jia-XiCheng,MilivojR.Belic,Zheng-LongHu,andYuanZhao,Dynamicsofnonlinearwavesintwo-dimensionalcubic-quinticnonlinearSchrodingerequationwithspatiallymodulatednonlinearitiesandpotentials[J].OPTICSEXPRESS,2016,24(9)：10066～10077.

[23]Z.Y.Zhang,andS.J.Xiong,Effectoflayer-thicknessrandomnessongapsolitonsandopticalbistabilityinnonlinearsuperlatticeswithphotonicstopgaps[J].Phys.Rev.B,1997，(55)：10302～10306.

文章编号：2095-4654(2016)05-0001-05

* 收稿日期：2016-02-01

中图分类号：TN929.11

文献标识码：A