任务驱动，引导学生思维不断向前伸展——“多边形的内角和”教学实录和反思

◇严育洪

任务驱动，引导学生思维不断向前伸展
——“多边形的内角和”教学实录和反思

◇严育洪

“多边形的内角和”是苏教版数学四年级下册“综合与实践”领域的内容，属于规律探索类课型。教材安排这一实践活动的价值不是仅仅得出一个结论，而是重在让学生经历规律探索的过程与方法，积累数学活动经验，发展学生的思维。

一 任务驱动：由“十六边形的内角和”开场

师：三角形有几个内角？

生：3个。

师：四边形有几个内角？

生：4个。

师：十六边形有几个内角？

生：16个。

师：我们已经知道，三角形的内角和是180°，那谁知道十六边形的内角和是多少度？

（学生面面相觑）

师：要研究十六边形的内角和，我们可以从几边形的内角和开始想起？

生：三边形。

【反思】由三角形的内角和突然提出十六边形的内角和问题，学生无法一下子获得结果，于是这一问题就成了一个悬念，也成了学生迫切想解决的问题，驱动学生自觉进行由简单到复杂的研究。

二 任务重心：从“四边形的内角和”展开

（一）唤醒。

师：（出示三角尺）三角尺有什么用？

生：可以用来画三角形。

生：可以用来测量直角。

生：可以用相同的三角尺拼出平行四边形、长方形、三角形。

师：是的，我拿的这个三角尺是个特殊的直角三角形，它的内角和是多少度？

生：这个直角三角形的内角和是180°。

(如图1演示)

师：这个三角形特殊吗？它的内角和是多少度？

图1

生：它是等腰三角形，内角和还是180°。

（如图2演示）

师：现在我们看到的是一般三角形，它的内角和是多少度？

图2

生：不管是什么三角形，内角和都是180°。

【反思】最简单的多边形是“三边形”，也就是三角形，所以“三角形内角和”是“多边形内角和”的知识起点。另外，两个完全一样的三角形可以拼成一个特殊的四边形，这一活动经验也可以成为学生探究四边形内角和的生长点，进而发现多边形都可以分割成三角形来研究内角和。

（二）攻关。

1.长方形的内角和。

师：从三角形的内角和，你想到了什么？

生：想到了四边形、五边形、六边形……的内角和。

师：你觉得四边形的内角和会是多少度？

生：我想三角形3个内角的和是180°，180°除以3，每个角就是60°，四边形有4个内角，内角和就是 60°×4=240°。

生：我觉得可能是360°。

师：你为什么觉得是360°？

生：正方形和长方形的内角和是90°×4=360°，由此我猜想四边形的内角和都是360°。

师：这个同学的探究思路很好，他先从特殊的想起，然后进行大胆的猜想。好，现在他的问题是其他四边形的内角和是不是360°，我们继续研究。

2.直角梯形的内角和。

（如图3演示，师给出能用三角尺量角的特殊直角梯形）

图3

师：要求这个直角梯形的内角和，我们需要知道另外两个角的度数。有量角器的同学可以量一量，没有量角器的同学可以用三角尺试着拼一拼。

[学生测量。反馈时，教师特别展示采用拼三角尺测量的学生的作品（如图4和图5），得到这个梯形的内角和是 90°+90°+120°+60°=360°]

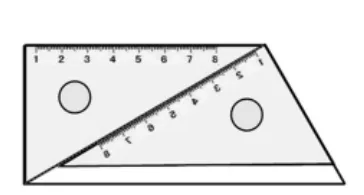
图4

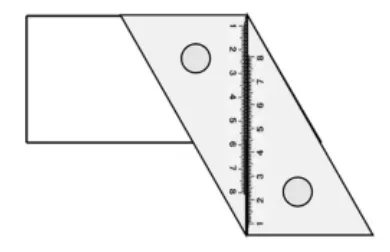
图5

师：像图4这样拼，如果把三角尺拿掉，会留下一条线段，恰好把这个梯形分成了2个三角形（如图6）。看了这张分割图，如果不量，你能看出这个梯形的内角和是多少度吗？

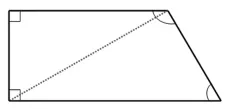
图6

生：可以，它分成了2个三角形，所以它的内角和是 180°×2=360°。

师：这样分呢？（如图7）

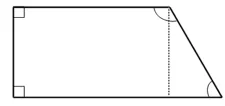
图7

生：分成了1个长方形和1个三角形，360°+180°=540°……（喃喃自语）怎么多了 180°？

师：是啊，怎么多了 180°？

生：我知道，把这个梯形分成1个长方形和一个三角形后，多出来2个直角，这2个直角不是梯形的内角（如图8），所以要减去180°。

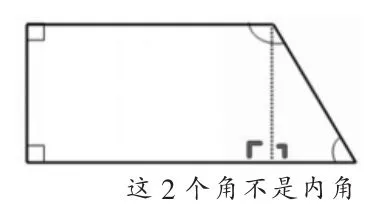
图8

（观察这些图形分割后的情况，如图9）

图9

师：你觉得哪种分割方法便于计算呢？分的时候有什么诀窍？

我国城市马拉松与国外相比起步比较晚，美国波士顿马拉松开始于1897年，是全球首个城市马拉松比赛，中国最早开展马拉松的城市北京成功举办首届马拉松在1981年比美国晚了100多年。还有人们观念的滞后，越来越重的生活压力迫使人们把精力过多的放在了经济条件的改善方面，忽视了对身体和精神的充实。随着时代的发展、人们观念的更新，国家对体育越来越重视，同时也看到了体育给国民带来的好处，马拉松作为城市发展的一个载体，越来越受到有识之士的关注。国内各个城市国内有条件的城市可以加强有马拉松比赛经验城市的交流与合作，充分利用城市资源积极筹办马拉松赛。

生：都分成三角形，这样算起来比较方便。

生：分的时候要连接顶点。

3.一般四边形的内角和。

师：我们现在已经知道长方形、直角梯形这些特殊四边形的内角和是360°，那么，是不是任意四边形的内角和都是360°呢？

（学生画任意四边形进行研究，发现四边形的内角和都是360°。在展示一个学生以下作品时，如图10，有同学提出还可以连接这个图形上面的2个顶点，如图11。“结果不可能是0°啊！”学生纷纷感到困惑。对这一生成，教师这样应对：“第二个同学的添补法，在计算内角和时，问题出在哪儿呢？大家不妨课后研究。”）

图10

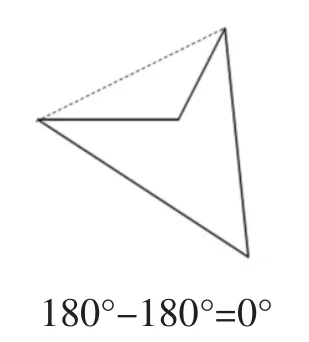
图11

【反思】对四边形的内角和，学生产生了两种想法。为了判断哪个是正确的，接下来的研究便成了学生的自觉行为，也就是说，继而开展的教学活动成了学生的内在需要。在探究活动的设计中，教师利用一个能够采用三角尺量角的特殊梯形，一方面量出了角的度数，从而算出四边形的内角和；另一方面在不同摆拼三角尺的方法中巧妙地留下了痕迹，引出分割线，启发学生根据分割成的已知内角和的图形直接得到梯形的内角和，进而从特殊到一般自然地引向任意四边形内角和的研究。在各种分割方法的比较中，学生清楚地发现便于计算的分割方法。对生成问题的处理，由于时间关系，留作课后研究，让学生带着问题走出课堂。

三 任务推进：向“多边形的内角和”攀登

师：我们已经知道四边形内角和为360°，顺着这样的结果，如果我们接着猜想，下一个你会想到什么？

生：我会想到五边形的内角和。

生：严老师，我才不上您的当呢。五边形内角和应该是540°，因为它可以分成3个三角形。

（生在黑板上画了1个五边形，然后把它分成了3个三角形）

师：那其他五边形是不是这样呢？大家要不要画画看看？

生：不画也能想得出来，五边形内角和就是540°。

师：好，我们接下来该研究谁的内角和了？

生：（齐）六边形的内角和。

生：（发现新大陆似的）严老师，六边形内角和才是720°呢！因为它可以分成4个三角形，180°×4=720°。

师：是这样吗？

生：（齐）是！

（突然有一个学生在黑板上画了这样1个七边形，如图12。在其他学生从七边形内部分割成5个三角形（如图 13）算出 180°×5=900°后，这个学生在七边形外部进行了这样的顶点连接，如图14，“狡猾”地对大家提出了这样一个问题：“这样连接该怎么算呢？”学生傻了眼，窃窃私语。终于有一个学生说：“我感觉这个问题同前面那个留到课后研究的问题是一样的。”同学们表示认同）

图12

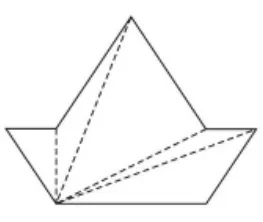
图13

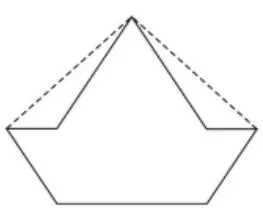
图14

师：嗯，确实是这样。这个问题也留给大家课后研究。

师：到现在你能完成课一开始提出的“十六边形的内角和”这个任务了吗？也就是十六边形的内角和该怎么算？

生：16-2=14，180°×14。

师：你是怎么想到16减2的？

生：其实，这里面是有规律的……

[教师根据该生的回答呈现下面的表格，概括出：多边形的内角和=（边数-2）×180°]

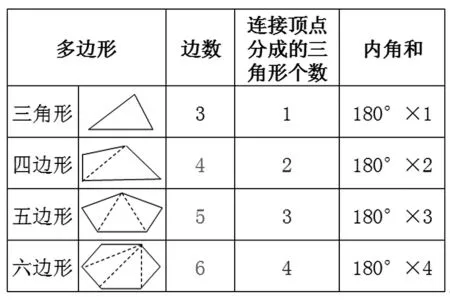
【反思】在学生研究循序渐进进入五边形内角和时，教师换了一种教学方式，故意设置陷阱，旨在检验学生是否会主动调用已有学习经验。面对五边形时，学生大多能够脱离实物通过表象操作获得正确的答案。接下来，从六边形内角和直接跳到十六边形内角和，旨在检验学生是否已经意识到这些数据之间存在着一定关联，促使学生通过寻找规律来解决问题。

四 任务延伸：为“多边形的外角和”铺垫

（一）回顾。

师：回顾刚才探究多边形内角和的过程，我们首先是从几边形开始研究的？

生：从四边形开始的。

师：如果把以前学过的知识包括在内，那么整个探究从哪里开始？

生：从三角形开始。

（板书：从简单到复杂）

师：我们在探究四边形的内角和的时候，又是从什么情况开始想的？

生：从特殊的长方形开始。

（板书：从特殊到一般）

（二）展望。

师：是的，从简单到复杂、从特殊到一般是常用的探究思路。另外，在探究过程中，由此及彼也是常用的思考方法，例如由三角形的内角和想到四边形、五边形等多边形的内角和。你能从多边形的“内”角和想到什么呢？

生：可以想到多边形有没有外角和。

生：严老师，多边形的外角是什么意思呀？

师：问得好！多边形有没有外角？如果有，多边形的外角和会是怎样的呢？这些问题将在中学数学中研究。

【反思】一堂课的结束，并不意味着知识的结束，也并不意味着学习的结束。要使学生保持探究的热情，就要让我们的教学有“问题”。本节课中，至少有两个遗留问题：第一个是课中生成的凹多边形内角和问题，第二个是课终联想到的多边形外角和问题。从近期看，让学生带着问题走出课堂，从远期看，又让学生带着问题走进中学。

（作者单位：江苏无锡市锡山教师进修学校）