基于球形杀伤元运动特性的明胶靶标标定方法研究

刘飞，单永海，张俊斌，宫小泽（中国白城兵器试验中心，吉林白城137001）



基于球形杀伤元运动特性的明胶靶标标定方法研究

刘飞，单永海，张俊斌，宫小泽
（中国白城兵器试验中心，吉林白城137001）

摘要：为研究使用明胶靶标对杀伤元进行杀伤威力评估的工程方法，分析明胶靶标的材料力学性能，在实验研究的基础上，结合瞬态动力分析软件对球形杀伤元在明胶介质中的运动规律进行了分析研究。研究结果表明：在使用明胶靶标进行威力实验前，应对靶标材料特性进行标定；球形杀伤元在明胶介质中高速运动时会产生空腔现象，最大空腔直径会随着侵彻深度的增加而增大，杀伤元的速度、阻力均以指数形式衰减；杀伤元以中高速（300～1 000 m/s）侵彻明胶靶标时，可将明胶靶标简化为流体模型。通过实例分析、计算，建立了速度与位移的数学关系，确定了明胶靶标的标定方法。研究结果可为杀伤元威力评估和明胶靶标标定提供参考。

关键词：兵器科学技术；球形杀伤元；侵彻；明胶；运动规律；数值仿真

0　引言

在轻武器终点杀伤效应研究中，明胶靶标作为一种肌肉组织模拟靶标被广泛地应用于杀伤元威力实验中。近年来，许多学者开展了相关的研究工作。金永喜等［1］建立了明胶靶标与肌肉目标瞬时空腔效应的等效关系。文献［2-4］通过数值仿真手段，对杀伤元侵彻明胶过程中的速度、能量、压力变化进行了科学分析。黄珊等［5］针对典型小口径枪弹侵彻明胶压力波特性开展相关实验研究。这些实验中均采用了10%与4℃的明胶靶标进行实验。由于明胶靶标在制备过程中涉及材料选取、相容、冷凝、保温、储存等众多环节，且明胶作为一种较软的高分子材料对温度和应变率较敏感［6-8］，同时，在高应变条件下，明胶靶标的物理参数测量还存在一定困难，这些问题导致明胶靶标理化性能不够稳定，影响试验数据的一致性和可对比性。因此，如何对影响杀伤元侵彻性能的明胶参数进行试前标定，保证实验数据的一致性、可对比性，成为一个迫切需要解决的问题。

为了科学建立标定弹道明胶参数的方法，并方便对杀伤元威力进行的研究，需要建立杀伤元侵彻明胶的力学模型。相对于枪弹和不规则破片，球形破片在侵彻明胶过程中具有无翻滚、无破碎、变形小等特点［1-4］，便于建立相关力学模型，许多学者就此开展了相关研究。Nenntiel［9］认为球形破片在明胶中受到的阻力为，其中ρ、v、A分别为明胶介质密度、破片速度和迎风面积，CD为动态阻力系数，且在一定时间间隔内为常数；Strurdivan［10］认为球形破片在明胶中只受惯性力和粘性力的影响，并引入惯性阻力系数CL和粘性阻力系数CV，该系数均需要通过实验标定；Seglers［11］认为球形破片在明胶中的受力情况与明胶的应变率有关，并引入基于应变率的强度模型。Peters［12］认为球形破片在明胶中的运动受到惯性力和明胶自身强度影响，且明胶自身强度取决于侵彻速度。刘坤等［13］认为球形破片在明胶中的运动受到惯性力、粘性阻力和明胶自身强度影响，并根据球形破片侵彻明胶靶标实验数据拟合得到了惯性和粘性阻力系数。温垚珂等［14］对高应变率下明胶靶标的本构模型进行了研究，认为在高应变率下，其物理响应可以用一定形式的动载本构关系（流体弹塑性本构）予以近似。从国内外相关研究可以得出，高速破片侵彻明胶靶标，明胶可作为流体模型进行计算。同时，上述学者给出的模型基本属于理论研究层面，模型相对复杂且需要测试和获取的有关参数较多，有些参数因测试技术不够成熟而难以获取，并且参数的增多势必导致实验样本的增大。

本文从工程试验角度出发，分析了明胶材料特性，并在大量实验研究基础上，结合瞬态动力学仿真软件LS-DYNA，对球形杀伤元在明胶介质中的运动进行了分析研究。得出了杀伤元在明胶靶标运动过程中的弹道变化规律，进一步明确了高速破片侵彻明胶靶标时，可将明胶作为流体模型进行相关的受力分析。通过流体动力学受力分析，建立了反映杀伤元速度衰减规律的数学模型，该模型参数较少，便于获取，易于建模；基于该模型，提出了仅通过中高速（200～1 000 m/s）球形杀伤元侵彻明胶实验，便可对影响弹道明胶侵彻性能参数进行有效标定，并给出相应的标定方法，达到了事半功倍的目的。研究成果通过了实验验证并可有效应用于弹药威力实验及评估工作中。

1　明胶靶标材料力学性能分析

明胶属于肽分子聚合物质，是从动物皮肤、结缔组织、骨头中提取的一种胶原蛋白，它为无味、无色（略带浅黄色）、半透明、坚硬的非晶态物，其不溶于有机溶剂，它吸水性强、粘度高。Cronin等［6］的研究表明温度对明胶靶标的力学性能具有较大影响。明胶靶标通常采用的温度一般在4℃～10℃之间。下面以几个典型温度点为例，考察明胶靶标温度对力学性能的影响。

由表1可以看出，靶标温度对屈服应力、最大应力和剪切模量影响较大。明胶靶标的屈服应力及剪切模量的变化，势必导致不同杀伤元对明胶的侵彻效果有所不同。杀伤作用实验研究中，通常需要使用高速摄影、测速仪器等测试设备，靶标从保温条件下取出放到实验指定位置后，还需一定的准备时间才能开始射击实验。在这个阶段，由于环境温度通常高于靶标温度（靶标温度4℃），靶标与外界进行热量交换，靶标性能会随放置时间而产生变化。而且即使在相同温度及浓度条件下的明胶靶标，由于制备工艺的不同也会导致明胶靶标的强度有所差别。张业聪等［15］以猪原皮为原材料提取明胶，研究了蒸胶过程中温度、pH值、时间等对明胶强度的影响，得出温度、pH值、时间等均会对明胶强度产生较大影响。根据研究结论，进行了不同溶解温度条件下明胶靶标强度实验。在明胶靶标熬制过程中会涉及溶解步骤，即明胶颗粒溶于水形成明胶溶液的过程。明胶靶标制作过程中通常采用水浴加热的方式加速明胶粉末的溶解，加热温度决定明胶溶解的速度，温度越高溶解速度越快。通常采用的温度一般在50℃～90℃之间。下面以60℃、80℃为例，考察加热温度对力学性能的影响，由表2可以明显的看出，熬制温度的确会对明胶的屈服应力及剪切模量产生较大影响。

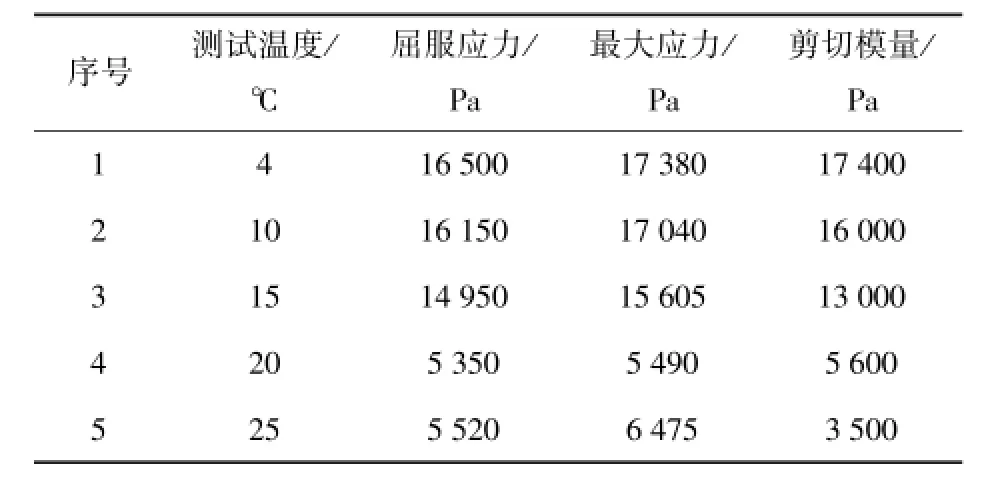
表1　不同温度条件下明胶的力学性能Tab.1 Mechanical properties of gelatin at different temperatures

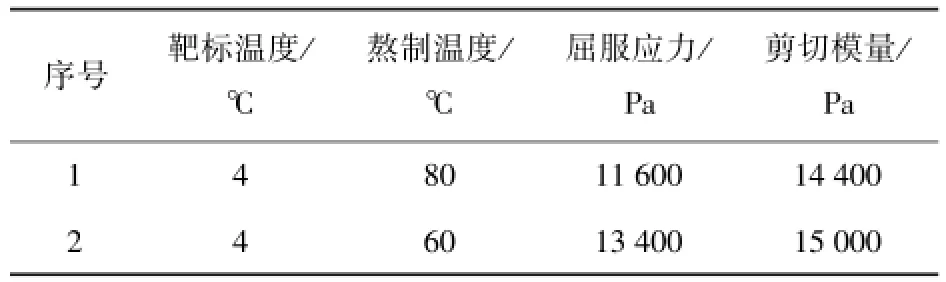
表2　不同制备温度条件下明胶的力学性能Tab.2 Mechanical properties of ballistic gelatin at different preparation temperatures

由此可见，使用明胶靶标进行威力实验研究过程中，熬制工艺、实验准备等诸多因素都会对明胶靶标的强度产生较大影响。因此有必要在试验前对影响杀伤元侵彻性能的明胶靶标的材料性能进行标定验证，以保证实验数据的一致性和可重复性。

2　球形杀伤元侵彻明胶的实验研究

为研究一种简单的明胶靶标材料性能标定方法，需要建立杀伤元侵彻明胶的力学模型，球形杀伤元相对其他杀伤元具有独特优势，因此进行了球形破片以不同速度侵彻明胶的实验。实验采用弹道枪以不同初速（300～1 000 m/s）发射直径4.8 mm的球形破片射击10%与4℃的弹道明胶，共进行了4组不同速度段的实验，每组均进行了多发射击实验以保证结果的一致性。实验测试方案如图1所示，使用光电靶测速系统记录球形破片侵入明胶的靶前速度；使用高速摄影系统记录球形破片在明胶中的运动过程及空腔变化情况。表3给出了不同速度段的典型实验结果，其中948 m/s和721 m/s为高速段实验速度，一般步枪弹的枪口速度及部分杀伤榴弹的破片速度（有效杀伤距离内）在这个范围内；535 m/s和359 m/s为中速段实验速度，一般手枪弹、军用霰弹枪的枪口速度在这个范围内。

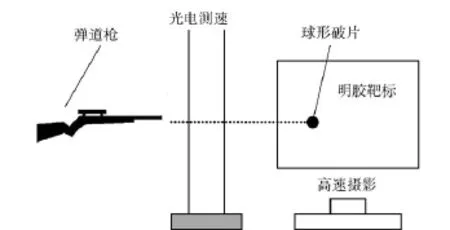
图1　杀伤元侵彻弹道明胶测试方案Fig.1 Test scheme of penetration of projectile into gelatin

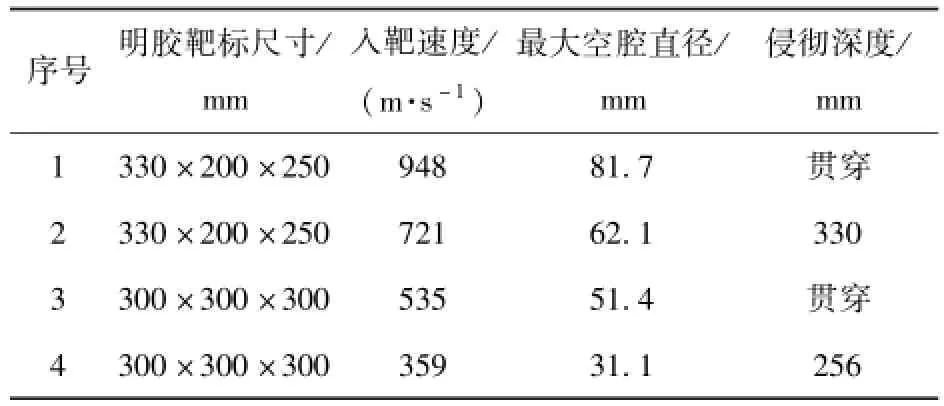
表3　球形杀伤元侵彻10%与4℃明胶的实验结果Tab.3 Experimental results of penetration of spherical projectile into 10%/4℃ gelatin

实验中观察到球形杀伤元在侵彻弹道明胶中空腔的形成、膨胀、收缩及脉动情况，并得到了相关的速度、位移（杀伤元在明胶内的位移即为侵彻深度）随时间的变化曲线，如图2所示。从表3可以看到，侵彻速度为948 m/s时，最大空腔直径可以达到杀伤元直径的17倍；当速度减小到359 m/s时，最大空腔直径约为杀伤元直径的6.5倍。可见侵彻速度对瞬时空腔效应影响较大。

3　球形杀伤元侵彻试验分析及标定方法建立

3.1有限元模型建立

为了科学分析杀伤元侵彻规律，进行了数值仿真试验。仿真采用与实弹实验对应1∶1的有限元求解模型，采用Lagrange算法，全部用Solid164实体单元，在球形杀伤元与明胶界面间采用面面侵蚀接触*CONTACT_ERODING_SURFACE_TO_SURFACE算法。在进行网格划分时，球形杀伤元与明胶的直接接触区及附近划分为较密的网格，而使远离弹道的区域网格尺寸逐渐增大，如图3所示。观察实验后的球形杀伤元，发现无明显变形，因此球形杀伤元采用刚体模型*MAT_RIGID以提高计算效率，球形杀伤元的材料参数如表4所示。

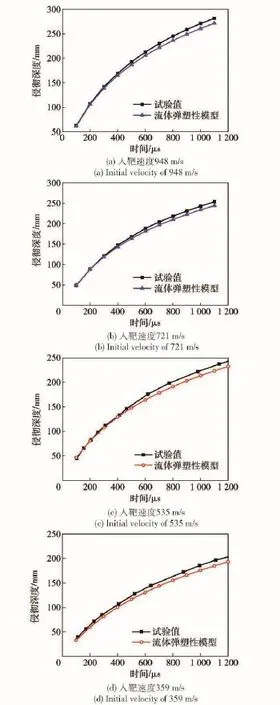
图2　不同速度下的侵彻深度随时间变化Fig.2 Initial penetration depth versus time at different speeds

图3　明胶有限元网格模型Fig.3 Finite element mesh model of gelatin

表4　杀伤元材料参数Tab.4 Mechanical properties of projectile material

软体材料明胶可采用*MAT_ELASTIC_PLASTIC_HYDRO材料模型和*EOC_LINEAR_POLYNOMIAL材料状态方程来描述，并参考相关文献［2-4］，明胶对应材料参数由表5给出。

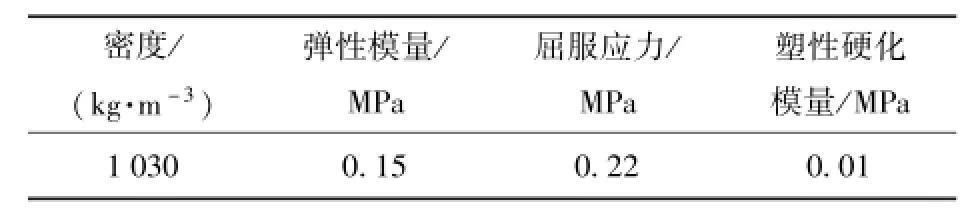
表5　明胶材料参数Tab.5 Mechanical properties of gelatin

设定球形杀伤元的入射速度分别为948 m/s、721 m/s、535 m/s和359 m/s.从位移-时间曲线对比（见图2）中可以看到，在不同速度段上的仿真模型的仿真结果均与实验结果较一致，相对误差均小于5%.所以，球形杀伤元以中高速侵彻明胶时，仿真流体模型能较好模拟明胶的物理响应。

3.2有线元计算结果与分析

针对以上模型，当球形杀伤元以不同速度侵彻明胶时，通过计算仿真可得到不同时刻的明胶内的压力、速度、位移变化等。以948 m/s的球形杀伤元侵彻明胶靶标为例，图4为不同时刻弹丸周围明胶的压力云图。同时，该图也反应出了垂直于弹道方向明胶微元的位移变化。从图4可知，杀伤元在明胶介质中运动时会产生空腔，而空腔的形成对杀伤元的弹道有着重要的影响。当杀伤元开始运动后，首先产生与明胶的撞击作用，在紧接撞击作用之后，明胶就被杀伤元带入运动状态。在这个阶段，通过杀伤元的速度衰减曲线（见图5）可以看出，作用于杀伤元上阻力随速度减小而减小，撞击后明胶从杀伤元侧面分开，空腔开始形成。随着杀伤元沿着其轨道前进，空腔变得越来越长，尾部会逐渐的扩大。

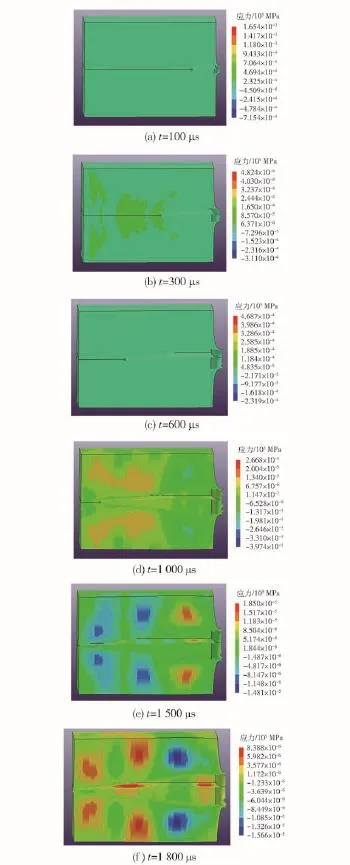
图4　不同时刻杀伤元周围明胶的压力云图Fig.4 Stress nephograms of gelatin around projectile at different times

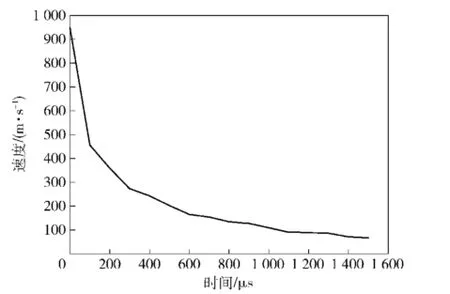
图5　杀伤元速度随时间变化曲线Fig.5 Projectile speed versus time

3.3杀伤元运动模型

结合实验及仿真结果，仍以948 m/s球形杀伤元侵彻明胶块为例，绘制杀伤元的速度-时间、速度-位移曲线，如图6所示。由图6可见，杀伤元在明胶介质中运动速度随时间及位移均呈指数规律下降。

通过前文文献调研及仿真模型验证，拟采用流体动力学理论对中高速杀伤元侵彻明胶靶标的物理过程进行分析。设杀伤元密度为ρp，以速度ux在密度为ρ、粘滞系数为μ的流体中运动，杀伤元正面受到阻力″.为简化计算模型，忽略重力作用，且不考虑温度和杀伤元翻滚的影响，则根据动量方程和牛顿第二定律有

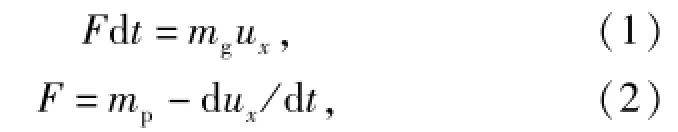
式中：mp为杀伤元质量；mg为dt（单位时间）作用于杀伤元头部正面液体质量。

设杀伤元长度为L，有效截面积为S，则

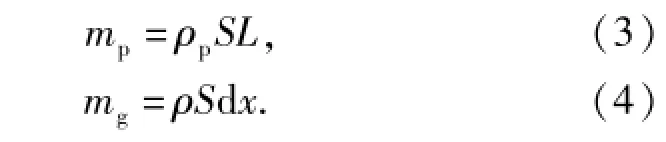
由于杀伤元在运动过程中受到明胶介质作用，运动姿态及杀伤元形状发生改变，设其有效受力长度及面积满足线性变换关系：

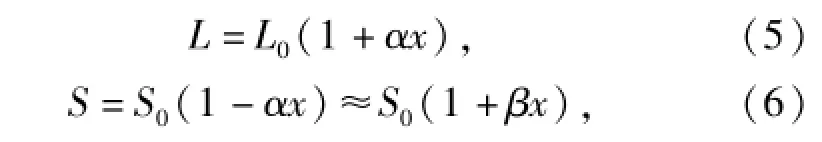
式中：x为杀伤元质心位置；L0和S0是杀伤元初始有效受力长度和截面积。杀伤元为实心弹体，总体体积V不变，其体积V=SL=S0L0（1+αx）（1+βx），则其中α和β是符号相反的变量。

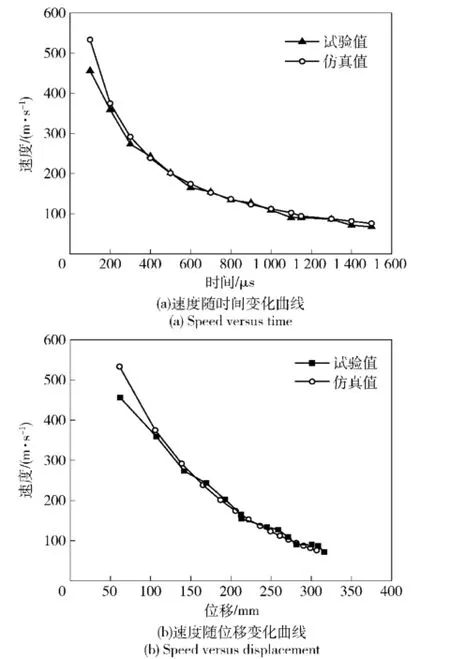
图6　球形杀伤元侵彻明胶速度随时间及位移变化曲线Fig.6 Speed versus time and displacement of small steel ball penetrating into gelatin

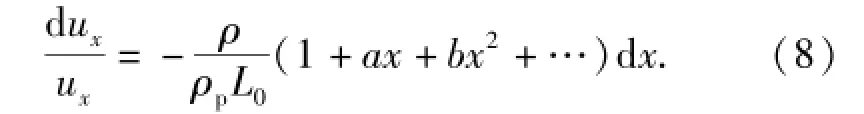
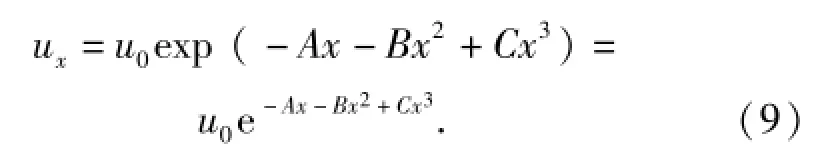
根据实验结合仿真数据拟合曲线可求得系数A、B、C，即得到杀伤元在明胶介质中任意点处的速度位移公式［16-17］：

实验中的球形杀伤元近似为刚体［2-3］，L0和S0不发生改变，同理可推导出：

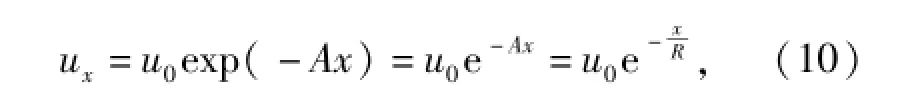
式中：R为存速系数，该系数主要受明胶靶标自身材料影响。

3.4明胶材料标定方法建立

通过球形杀伤元以948 m/s的速度正对明胶侵彻实验，拟合得到 A≈0.008 768，令 R=1/A≈114.045.由 （10）式可知，R越大，弹丸运动得越远，侵彻能力越强。通过球形杀伤元分别以721 m/s、535 m/s、359 m/s的实验验证模型及结果（见表6）不难证明（9）式、（10）式的正确性。此外还在相同速度（721 m/s）条件下，进行了2.5 mm钨球和钢球的侵彻明胶靶标的实验，钨球密度 ρW= 15.63 g/cm3，钢球密度ρs=7.83 g/cm3.根据（8）式可以看出，对于相同的明胶，ρW/ρs=2.00，因此衰减到相同速度时，钨球的侵彻深度应为钢球的2倍，实验验证结果如表7所示，进一步验证了模型的正确性。由实验结果可以看出，该模型误差较小。基于以上分析，该公式可用于指导实验，进而可通过初速u0及系数R或者A、B、C来判定杀伤元的威力或明胶材料性能。

基于（10）式进行明胶靶标材料强度标定，可通过3种方法实现：

1）速度校核法。即在每组实验前使用不同速度的刚性球形杀伤元对同一批次制备待标定明胶靶标进行侵彻实验。使用高速摄影或测速雷达测试杀伤元的速度及位移变化，然后根据（10）式对系数A 或R进行拟合，如果系数相同或误差符合实验要求，则这些组次的实验数据具有一致性和可重复性，可进行不同杀伤元（子弹、不规则破片等）对明胶靶标的威力实验，反之需要重新制作明胶靶标。表6和表7中所进行的实验就是采用该种方法进行的。

2）位移校核法。如果每次杀伤元侵彻实验均在固定距离上发射固定初速的相同材质及直径的球形杀伤元，若明胶靶标材料系数A或R相同，则对应杀伤元的位移x是固定不变的，当杀伤元速度趋近0时，即球形杀伤元未飞出明胶靶标，那么侵彻深度是固定不变的，因此也可采用侵彻深度对明胶靶标材料的强度性能进行标定。通过将保温后的明胶（5℃）放置在环境温度为15℃及30℃两种条件下，每隔一定时间，采用φ3 mm的钢质球形破片（初速200 m/s，设计距离10 m）进行射击，得出两种条件下时间对侵彻深度的影响，具体数据见表8.根据表8中的数据可以看出，侵彻深度和相对跳差随靶标放置时间增加而变大，且环境温度与原始温度温差越大，其变化越明显，在30℃的环境下放置2 h后，侵彻深度达到11.3 cm，相对跳差超过15%，说明该状态下的明胶靶标性能不稳定，不宜进行相关威力实验。

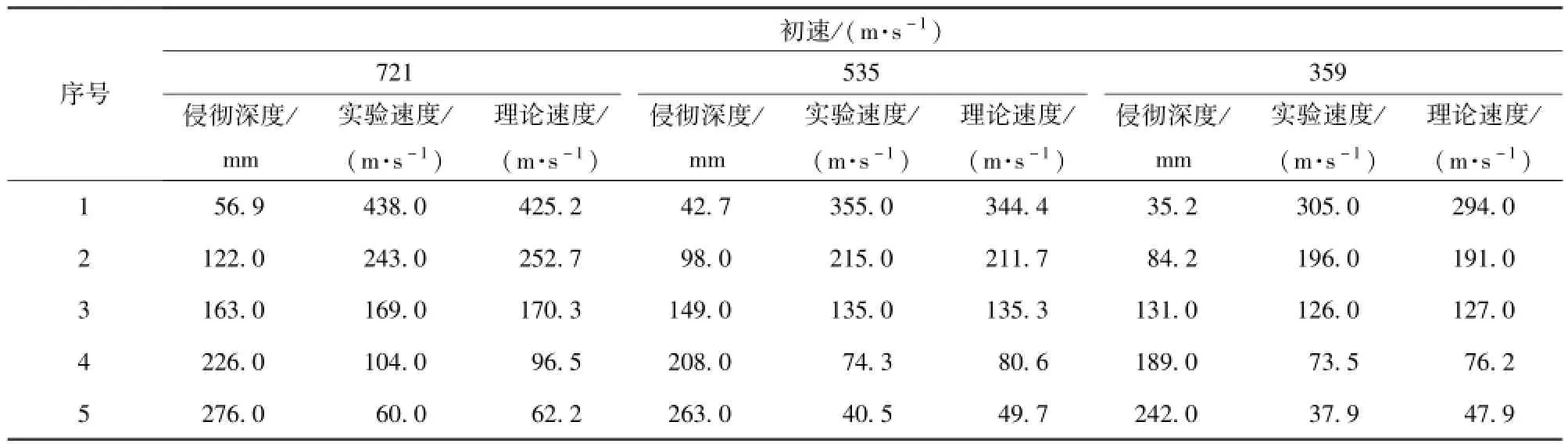
表6　实验值及理论计算结果Tab.6 Experimental data and theoretically calculated results

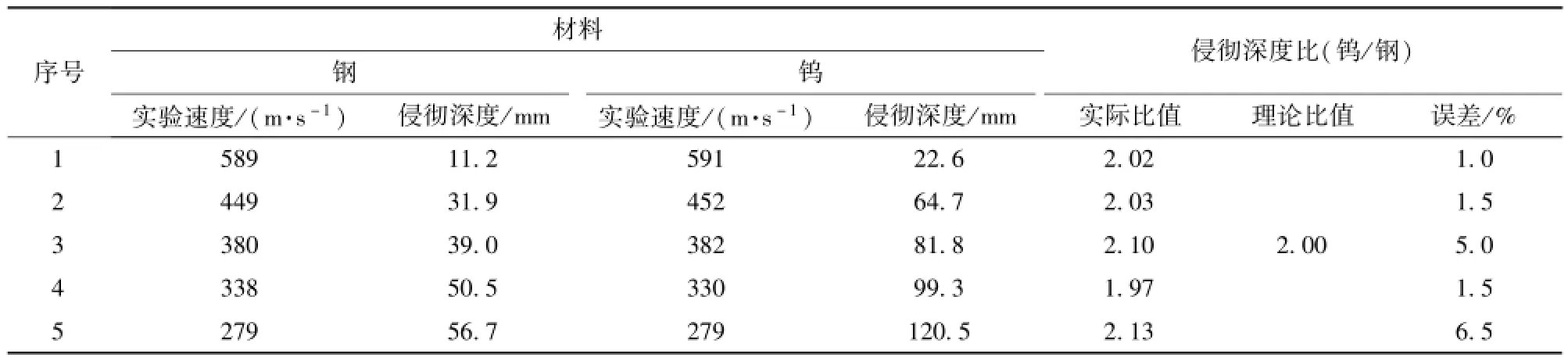
表7　实验值及理论计算结果Tab.7 Experimental data and theoretically calculated results

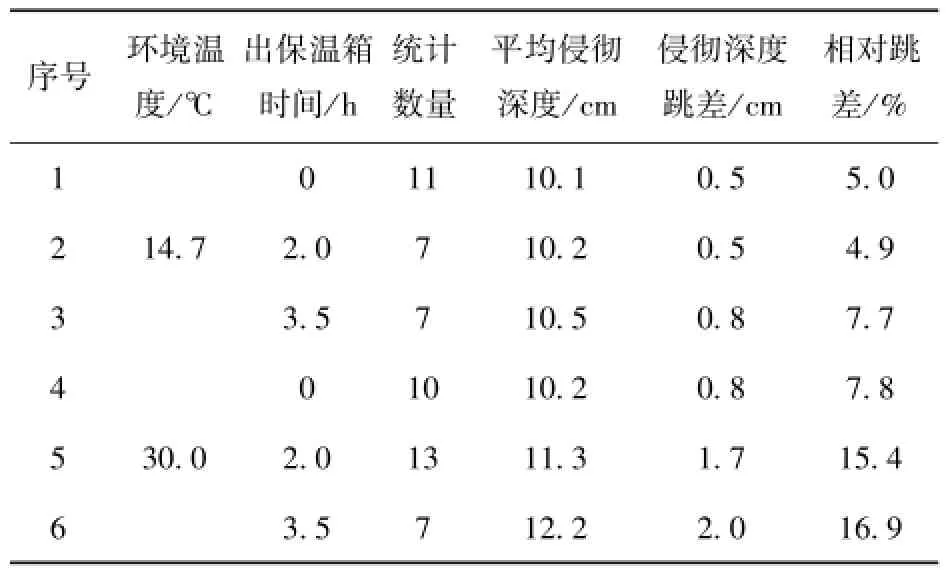
表8　10%与5℃配比的明胶放置时间和侵彻深度对比数据Tab.8 Storage time of 10%/5℃ballistic gelatin and penetration depth

3）时间校核法。仍采用方法2中的射击方式，在靶前、靶后分别布设激光靶或光幕靶等测时设备，对入靶和出靶时间进行测量。对于相同材质的明胶靶标，（10）式表明该球形杀伤元在明胶内的位移速度曲线应是相同的。因此，对于运动距离，即明胶靶标的长度相同，则弹丸飞出靶标前后的时间差或平均速度是相同的，就可以使用时间或平均速度对明胶靶标的材料进行标定，若数值相同，则材料性能相同，反之不同。该方法本质与方法1相同，只是测量参量不同。

由于模型是建立在流体模型的基础上，所以当杀伤元速度较低时，模型的速度误差相对较高。但如图6所示，低速杀伤元对侵彻深度的贡献不大，并且侵彻深度与初速强相关，初速越大，该模型误差越小。因此，速度校核法可以剔除低速状态下的实验数据，有利提高标定精度，但对测试设备要求较高；位移校核法主要测量侵彻深度，对测试设备要求不高，但会涉及低速阶段，存在一定误差；时间校核法对测试设备要求适中，且如果杀伤元初速较高，出靶速度也会较高，同样可以避免低速产生的模型误差，推荐使用。这3种方法各有利弊，实验人员可以根据实际情况进行适当选择。

4　结论

本文分析了明胶靶标的材料特性，并通过实验数据结合数值仿真方法对弹丸在明胶介质中运动规律进行了分析，对弹丸稳定运动的规律进行了计算，得到以下结论：

1）由于试前准备、熬制工艺等会对明胶靶标材料强度产生较大影响，因此在使用明胶靶标进行威力实验过程中，应对明胶靶标进行材料性能标定，以保证实验数据的一致性和可重复性。

2）球形杀伤元在高速侵彻明胶靶标时，会产生空腔现象，最大空腔直径会随着侵彻深度的增加而增大，杀伤元的速度、阻力均以指数形式衰减。

3）在侵彻试验等工程实践中，杀伤元以中高速（300～1 000 m/s）侵彻明胶靶标时，可将明胶靶标简化为流体模型，通过分析计算建立了杀伤元在明胶介质中任意点处的速度-位移公式：ux=u0· exp（-Ax-Bx2+Cx3）=u0e-Ax-Bx2+Cx3，并以球形杀伤元为特例对该模型进行了简化和验证。

4）基于球形杀伤元的速度-位移公式 ux= u0exp（-Ax）=u0e-Ax=u0e-Rx，提出了3种明胶靶标材料强度性能的标定方法，并对每种方法进行了分析讨论，比较了各自利弊，可为实验人员明胶靶标标定提供参考。

参考文献（References）

［1］ 金永喜，陈波，张敬敏，等.低侵彻步枪弹翻滚破碎机理研究［J］.兵工学报，2013，34（10）：1221-1226. JIN Yong-xi，CHEN Bo，ZHANG Jing-min，et al.Research on rolling and fragmentation mechanism of non-penetrating rifle bullets［J］.Acta Armamentarii，2013，34（10）：1221-1226.（in Chinese）

［2］ 罗少敏，黄拱武，陈爱军.球形弹丸侵彻明胶数值仿真分析［J］.计算机仿真，2012，29（11）：79-82. LUO Shao-mi，HUANG Gong-wu，CHEN Ai-jun.Numerical simulation analysis of spherical projectiles penetrating gelatin［J］. Computer Simulation，2012，29（11）：79-82.（in Chinese）

［3］ 温垚珂，徐诚，陈爱军，等.球形破片高速侵彻明胶靶标的数值模拟［J］.弹道学报，2012，24（3）：27-29. WEN Yao-ke，XU Cheng，CHEN Ai-jun，et al.Numerical simulation of spherical fragments penetrating into ballistic gelatin at high velocity［J］.Journal of Ballistics，2012，24（3）：27-29.（in Chinese）

［4］ 温垚珂，徐诚，陈爱军，等.步枪弹侵彻明胶靶标的数值模拟［J］.兵工学报，2013，34（1）：14-19. WEN Yao-ke，XU Cheng，CHEN Ai-jun，et al.Numerical simulation of the penetration of bullet on gelatin target［J］.Acta Armamentarii，2013，34（1）：14-19.（in Chinese）

［5］ 黄珊，王浩胜，王舒，等.典型小口径枪弹侵彻明胶压力波特性实验研究［J］.弹道学报，2013，25（1）：62-67. HUANG Shan，WANG Hao-sheng，WANG Shu，et al.Experimental study on pressure-wave characters in the process of typical small-caliber bullet penetrating gelatin［J］.Journal of Ballistics，2013，25（1）：62-67.（in Chinese）

［6］ Cronin D S，Falzon C.Characterization of 10%ballistic gelatin to evaluate temperature，aging and strain rate effects［J］.Experimental Mechanics，2010，51（7）：1197-1206.

［7］ Parker N G，Povey M J W.Ultrasonic study of the gelation of gelatin：phase diagram，hysteresis and kinetics［J］.Food Hydrocolloids，2012，26（1）：99-107.

［8］ Salisbury C P，Cronin D S.Mechanical properties of ballistic gelatin at high deformation rates［J］.Experimental Mechanics，2009，49（6）：829-840.

［9］ Nennstiel R.Once again-spheres in gelatin［J］.The Journal of Trauma，1990，6（2）：119-123.

［10］ Sturdivan L M.A mathematical model of penetration of chunky projectiles in a gelatin tissue stimulant，ARCSL-TR-78055［R］. MD，US：Aberdeen Proving Ground，1978.

［11］ Segletes S B.Modeling the penetration behavior of rigid spheres into ballistic gelatin，ARL-TR-4393［R］.MD，US：Aberdeen Proving Ground，2008.

［12］ Peters C E.A mathematical-physical model of wound ballistic ［J］.The Journal of Trauma，1990，6（2）：303.

［13］ 刘坤，吴志林，徐万和，等.球形破片侵彻明胶修正力学模型［J］.南京理工大学学报，2012，36（5）：25-31. LIU Kun，WU Zhi-lin，XU Wan-he，et al.Correction mechanical model of spherical fragments penetrating gelatin［J］.Journal of Nanjing University of Science and Technology，2012，36（5）：25-31.（in Chinese）

［14］ 温垚珂，徐诚，陈爱军，等.高应变率下弹道明胶的本构模型研究［J］.兵工学报，2014，35（1）：128-132. WEN Yao-ke，XU Cheng，CHEN Ai-jun，et al.Study of constitutive model of ballistic gelatin at high strain rate［J］.Acta Armamentarii，2014，35（1）：128-132.（in Chinese）

［15］ 张业聪，付丽红.明胶冻力影响因素的研究［J］.皮革化工，2006，23（6）：8-12. ZHANG Ye-cong，FU Li-hong.Study of effect factors of gel strength of gelatin［J］.Leather Chemicals，2006，23（6）：8-12.（in Chinese）

［16］ Waugh J G，Stubstad G W.水弹道学模拟［M］.陈九锡，张开荣，译.北京：国防工业出版社，1979. Waugh J G，Stubstad G W.Water ballistics simulation［M］. CHEN Jiu-xi，ZHANG Kai-rong，translated.Beijing：National Defense Industry Press，1979.（in Chinese）

［17］ 杨莉，张庆明，时党勇，等.爆炸成型模拟弹丸对水介质侵彻的数值仿真［J］.弹箭与制导学报，2009，29（2）：118-119. YANG Li，ZHANG Qing-ming，SHI Dang-yong，et al.Numerical simulation for the penetration of explosively formed projectile into water［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2009，29（2）：118-119.（in Chinese）

中图分类号：TJ012.4

文献标志码：A

文章编号：1000-1093（2016）06-1117-08

DOI：10.3969/j.issn.1000-1093.2016.06.021

收稿日期：2015-01-15

基金项目：国家重大基础研究项目（613104）

作者简介：刘飞（1987—），男，工程师。E-mail：705226581@qq.com；单永海（1964—），男，研究员，博士。E-mail：yhsh68@163.com

Research on Calibration Method of Ballistic Gelatin Based on Motion Characteristics of Spherical Projectile

LIU Fei，SHAN Yong-hai，ZHANG Jun-bin，GONG Xiao-ze

（Baicheng Ordnance Test Center of China，Baicheng 137001，Jilin，China）

Abstract：In order to explore the method of using a gelatin target to assess projectile lethality，the mechanical properties of ballistic gelatin are analyzed，and the movement rule of spherical projectile in gelatin is studied based on the experimental research and the transient dynamic analysis software.The results show that the mechanical properties of ballistic gelatin should be calibrated before experiment；a cavity phenomenon may arise when the spherical projectile moves in the ballistic gelatin at a high speed，the max diameter of cavity increases with the rising of penetration depth，and the resistance and speed of projectile are reduced exponentially；and the gelatin target can be simplified as a fluid model when the projectile penetrate it at a high speed（300～1 000 m/s）.The mathematical relationship between velocity and displacement is established through example analysis and calculation，and a ballistic gelatin calibration method is proposed.

Key words：ordnance science and technology；spherical projectile；penetration；gelatin；movement rule；numerical simulation