大型复杂武器系统可靠性和维修性指标的总体优化方法

吕建伟，徐一帆，谢宗仁（海军工程大学管理工程系，湖北武汉430033）



大型复杂武器系统可靠性和维修性指标的总体优化方法

吕建伟，徐一帆，谢宗仁
（海军工程大学管理工程系，湖北武汉430033）

摘要：可用性是装备效能的重要组成部分，是装备常规技术性能得以发挥的前提。通过对大型复杂武器系统层次结构和可用度基本关系式的研究，采用数学分析方法确定了各分系统可用度指标协调改进的基本原理。研究了在工程实践中，各分系统的指标改进难度对改进次序的影响，设计了分系统级可用性和设备级可靠性维修性指标优化的计算方法并确定了算法流程。采用Matlab编程，以某型舰为例，检验了算法的可行性与有效性，给出了完整的计算示例，从而可为以最小的代价实现和改进装备总体可用度指标，使各分系统所属设备的可靠性和维修性指标形成一个整体的要求，提供理论依据和方法。

关键词：兵器科学与技术；武器系统；可用性；分系统和设备；可靠性；维修性；总体优化

0　引言

大型复杂武器系统一般具有多层结构，所属分系统和设备数量较多，多种作战剖面和作战样式等特点［1-2］。如何提高装备系统的效能，建立总体指标（如可用度）和分系统指标以及各分系统所属设备可靠性维和修性指标的关联关系，并在此基础上，根据指标传递和优化原理，着眼总体指标的快速改进，通过相关算法优化得到各分系统所属设备的可靠性和维修性指标，对于系统总体可用度以及整体作战效能的发挥具有重要意义。

大型复杂武器系统各个分系统所属的设备一般都具有一定的可靠性和维修性指标水平，这可以称为当前值，它们对于总体的可用度等指标具有决定性的影响。同时，如果我们要实现一定水平的总体可用度指标，对于各分系统所属设备的可靠性和维修性指标，又是有所要求和约束的。当二者协调或一致时，可以认为设备指标能够满足总体的要求。反之，为了满足总体的要求，就需要通过建模和分析，确定分系统和设备的可靠性和维修性指标改进的方向和差距大小等，这可以称之为武器装备可靠性和维修性指标的总体优化问题。

系统可用度等总体指标的综合影响包括总体指标的逐层传递、同层次指标的相互协调、对分系统和设备级指标的逐层制约和影响等。在该领域，韩坤等［1］以系统效能为目标对装甲车辆的可靠性、维修性、保障性和测试性指标进行了权衡分析；Charles等［3］以多目标优化的形式，采用遗传算法对于一类可修复系统的可用性进行了分配；毛德军等［4］在有限经费条件下，研究了装备底层备件的库存与订购策略问题，目标是优化总体的可用度；此外，文献［5-7］也对于装备总体指标与底层指标的关系进行了有益的探索。存在的问题是缺乏一种将装备的顶层总体指标（可用度）与分系统和设备的底层指标（可靠性和维修性）联系起来的，以底层指标的最小代价实现顶层指标的快速改进方面的研究，难以实现从总体的角度对底层设备的可靠性和维修性指标进行优化。本文以海军舰船为例，对总体可用度约束下的设备可靠性和维修性指标的优化问题进行研究，研究并建立总体可用度指标的模型和优化方法，实现分系统级指标的相互协调和整体优化，确定总体和分系统指标约束下的设备可靠性和维修性指标，从而以最小的代价实现和改进总体可用度目标，最大限度地发挥武器装备的常规作战能力。

1　总体模型的建立

舰船等装备存在的根本性目的，是为了及时、可靠、有效地执行各种任务。这意味着在需要时能及时出动（可用性A），在任务过程中可靠顶用（任务成功性D），并在执行任务过程中具有足够的能力（常规性能C）。美国工业界武器系统效能咨询委员会的效能评价模型WSEIAC（也称ADC模型［1，3］）可以对其进行基本的描述。

因此，装备在执行任务时常规作战能力发挥的前提，就是其各个组成部分的可用度以及设备的可靠性、维修性得到充分的保证，这些因素将共同支撑着装备常规能力的发挥［7］。

可用度A是通过可靠性指标MTB″和维修性指标MTTR计算得来的，其基本表达式［7-9］如（2）式所示。该式对于舰船等装备的各个层次如分系统、设备等级别都适用。

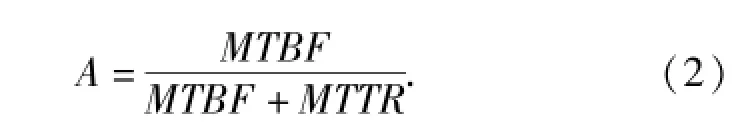
设定舰船等装备由各个分系统组成，分系统由设备组成，构成一个层次关系，如图1所示。

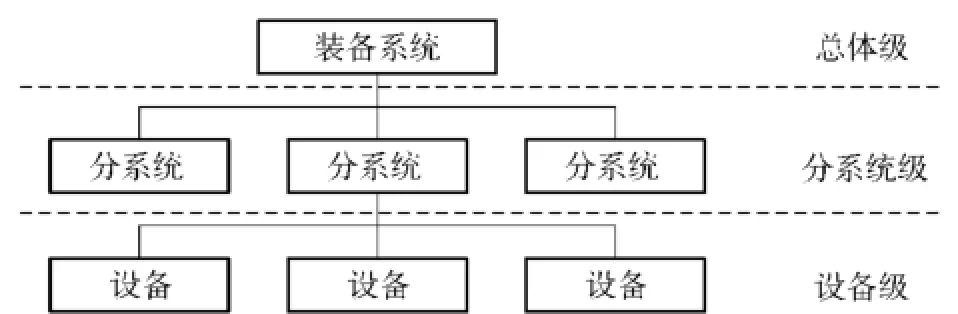
图1　装备的分系统和设备层次关系Fig.1 Hierarchical relationship of subsystems and equipment in a weapon system

假设通过使用分析和比较研究，已经确定了装备系统（全舰）的可用度初始目标值At.根据总体、分系统和设备的层次结构关系，可以认为总体可用性指标是分系统级指标的综合、分系统可用性是各个设备指标的综合。若分别以A和Ai（i=1，2，…，n）表示总体和各分系统可用度指标，根据文献［7］的分析，对于能够遂行多种作战任务的大型复杂武器系统，考虑其随时可以出动（投入使用）、对于故障要随时进行修复等要求，有

2　分系统和设备级指标的协调和优化原理

分系统级指标之间协调优化应以尽可能低的代价，依序改进“不协调”的分系统级可用度指标，从而快速有效地提高总体可用度指标，并满足规定的指标要求。

在以下推导中，为了表述方便，不妨设A1＜A2＜…＜An，若分别令A1→A1+δa，A2→A2+δa，…，An→An+δa.则有 A1→A1+δa时，A+δA=（A1+ δa）A2…An=A1A2…An+δaA2A3…An.

同理，有A2→A2+δa时，A+δA=A1（A2+δa）…An=A1A2…An+δaA1A3…An.

⋮

An→An+δa时，A+δA=A1A2…（An+δa）= A1A2…An+δaA1A2…An-1.

对以上各式比较可知，δaA2A3…An＞δaA1A3…An＞δaA1A2…An-1，由此可知，在总体由不同的分系统组成以及上述假设条件下，分系统可用度改进的优先顺序为A1，A2，…，An，这将使总体A指标得到最快的改进。

在（3）式基础上将各式进一步展开，有

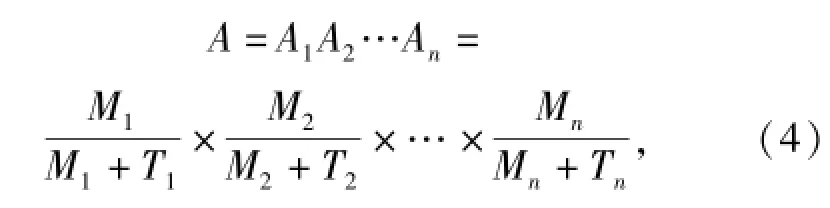
式中：Mi、Ti分别表示对应分系统的可靠性指标MTB″和维修性指标MTTR.（4）式清楚地表明：装备由分系统组成，总体可用度A由各分系统指标Ai的组合提供；分系统由设备组成，分系统可用度Ai由各设备的指标Aij的组合提供；设备可用度由其可靠性和维修性指标提供。

由于有A1＜A2＜…＜An，考虑T1，T2，…，Tn与M1，M2，…，Mn相比，一般都有T1≪M1，T2≪M2，…，Tn≪Mn，且有同类型设备或分系统T1，T2，…，Tn指标大小相近，所以一般都有M1＜M2＜…＜Mn（证略）。

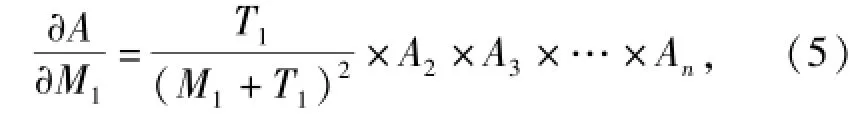
结论1：在总体由不同分系统组成的前提下，一般来说，优先改进（提高）可用度最低的分系统所对应的可靠性指标MTB″，将使总体A指标得到最快的改进。

其前提条件是：该分系统的可靠性指标MTB″有改进余地，即该指标处于其上下限范围内，最好是接近下限的位置。其中，下限由使用强度得到的设备级的可靠性指标MTB″计算确定，上限可在下限的基础上，由工程惯例和经验估算得到。

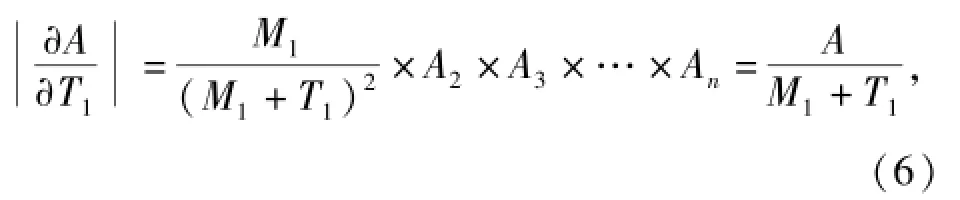
结论2：在总体由不同分系统组成的前提下，一般来说，优先改进（降低）可用度最低的分系统所对应的维修性指标MTTR，将比改进其他维修性分系统的指标MTTR，使总体A指标改进的幅度要大。

其成立的前提条件与结论1类似。

以上结论的成立需要较多的前提条件，尤其是T1，T2，…，Tn指标大小相近。在该条件不成立时，结论1和结论2以及对应的算法需要根据（5）式和（6）式等相应的计算结果进行调整。

比较（5）式和（6）式，还可以得出更多的结论，详见本文第4节中的相应分析。

3　分系统指标的加权处理

前述分析结论只是在理论上解决了问题。在实际工程应用中，在进行分系统指标的优化和协调计算时，还应考虑各分系统指标改进相同幅度的技术经济难度不同，对分系统指标进行加权处理。

首先定义αi为分系统i的可用度指标改进的难度系数，该系数可经由综合评估的方式得到。

因为加权对象的基值Ai＜1.0，所以αi数值越大，将导致加权后的效果（指标数值）越小。所以在进行常规的评估时，改进难度越大的分系统，难度系数可以设置得越大。评估完成后，在输出评估系数时，则需要将αi数值更新为αi=1-α′i.αi在（0，1）范围数值越小，说明Ai的改进难度越大。

在这样的考虑之下，原始的式子A=A1A2…An仍然成立，但是加权后得到的式子A′=×× …×就成为优化计算的对象。

4　算法设计及其流程图

这里结合工程应用的需要，给出实际的优化协调算法及其流程图。基本算法包括如下步骤：

1）通过作战研究和需求分析，得到的总体可用度要求值（使用指标）At.

2）通过分析和计算得到设备和分系统的可靠性指标MTB″初值（下限值），由类比等方法得到维修性指标MTTR（上限值）。

3）通过（2）式计算得到各分系统的可用度指标Ai（此处i为分系统下标，i=1，2，…，n）。

4）根据（2）式计算总体可用度指标A.

5）计算ΔA=A-At.如果ΔA≥0或ΔA＜0但|ΔA|＜ε，计算结束，否则转入步骤6（这里ε为许用误差）。

以上算法的原理流程图如图2所示。

基本算法主要适合从总体（全舰）到各分系统的优化计算，而以下扩展算法主要适合从分系统级到其所属设备的计算。

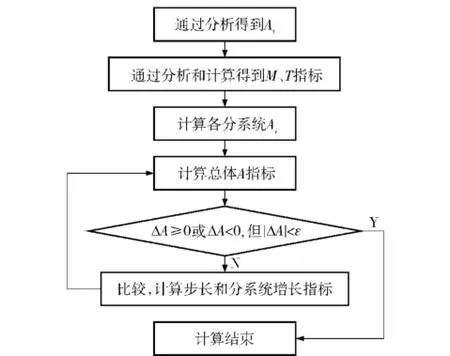
图2　装备各分系统可用度指标的优化和协调原理流程图Fig.2 Flowchart of optimizing and coordinating principles of subsystem availability

扩展算法是在基本算法的基础上所导出的，其原理相同，但是在指标处理的特色方面有所不同，基本算法直接处理可用度指标Ai，而扩展算法处理的则是可靠性Mi指标和维修性Ti指标。

扩展算法1（研究目标是Mi指标）：步骤1～步骤5与基本算法相同，差别在于第6步。

扩展算法2（研究目标是Ti指标）：步骤1～步骤5与基本算法相同，差别在于第6步。

扩展算法3（同时考虑Mi和Ti指标）：步骤1～步骤5与基本算法相同，差别在于第6步。

从以上各扩展算法的研究目标可知，扩展算法1对应着装备的可靠性专项工程，扩展算法2对应着维修性专项工程，而扩展算法3则对应着可靠性和维修性综合工程。在实际工作中可以根据装备研制的需要（例如根据用户的反映或者装备母型的使用情况），视情选用。如果仍然无法确定，建议采用扩展算法3，见下面的说明。

分析表明，在实施扩展算法3时，还可以采用4种不同的策略。

同步协调策略（算法编号3-1）：对于每一次迭代，都同时处理Mk和Tk.即每次迭代都同时使得Mk增大一个步长，同时使得Tk减小一个步长。在工程上，这对应着同步协调的开展装备的可靠性和维修性改进工作（可靠性维修性综合工程）。

灵活处理策略（算法编号3-2）：对于每一次迭代，都计算和比较，择其大者进行改进，而对较小者暂不处理。即每次迭代仅选择一个对于分系统可用度贡献最大的分量进行调整，使得Ak得到最快的改进，其原理可见对于（5）式和（6）式的对比分析。在工程上，这对应着在可靠性维修性综合工程中，视情灵活开展改进工作。

先M后T策略（算法编号3-3）：对于某次迭代中选定的单元j（j=1，2，…，nk，nk为分系统k中设备的数量），仅调整其Mkj指标。迭代反复进行，直至达到规定的可用度指标为止；若规定的可用度指标无法达到，则将Mkj指标换成Tkj指标，重复以上过程。这相当于对扩展算法1的改进。即在装备的可靠性和维修性综合工程中，应该先实施可靠性专项工程，若无法达到规定的指标，再实施维修性专项工程，直至目标达到为止。

先T后M策略（算法编号3-4）：与策略5的改进顺序相反，是对扩展算法2的改进。即在装备可靠性和维修性综合工程中，先实施维修性专项工程，若无法达到规定的指标，再实施可靠性专项工程，直至目标达到为止。

采用以上算法得出计算结束后，再采用常规方法［10］分别进行后续处理（如数据取整等）。限于篇幅，不再赘述。

5　示例计算

在以上工作的基础上，本节以某舰为例，给出针对各分系统及其所属设备的相关指标的协调优化计算示例。

5.1基础数据及其来源

按照功能进行划分，水面舰船可以划分为15～20个分系统，该型舰具体的系统组成［7］如图3所示（船体等系统略去），各系统的组成略。

图3　某型舰的主要分系统组成Fig.3 Main subsystems of a navy vessel

假设通过舰船全寿命分析、作战研究和类比分析等手段，确定总体可用度要求值At为0.92［10］，许用误差ε=0.000 01.通过调研和使用分析，各分系统所属设备的可靠性指标MTB″、维修性指标MTTR初始值以及对应的上下限均已确定（为简化问题起见，这里设定指标的初始值即为下限）。

5.2由全舰到各分系统的优化与协调计算

采用以上数据进行计算，可以得到该型舰17个分系统的可用度初始值（表1中仅列出了6个分系统，数据经脱密处理，下同），示于表1第3行中，由计算结果可知，当前全舰指标为 A=0.872 425，ΔA=0.027 575＞ε，达不到要求，需要进行优化计算。根据以上所得到的基本原理，可以初步得出各分系统指标改进的先后次序（表1第6行），但在此基础上还需要考虑各分系统指标改进的难度，即需要进行加权处理来确定实际应用中的改进顺序。

通过专家调查以及层次分析法等形式，计算可得各分系统指标改进的技术经济难度［7］，即分系统可用度指标的权系数，以及加权可用度指标、加权后的可用度指标的排序，均示于表1中。

结合表1第3和第5行的计算结果可以看出，权重系数（即指标改进难度系数）在分系统指标协调优化中对指标改进次序的影响（见图4）：原本动力分系统的改进次序先于副炮分系统，但由于动力分系统的指标改进难度较大，因而在加权处理后其改进次序后移，其先后次序发生了颠倒，这样也更加符合工程实际。

在分系统级优化过程中，采用基本算法并取δa=ε.采用 Matlab编程计算，优化结果见表 1 第8行所示。

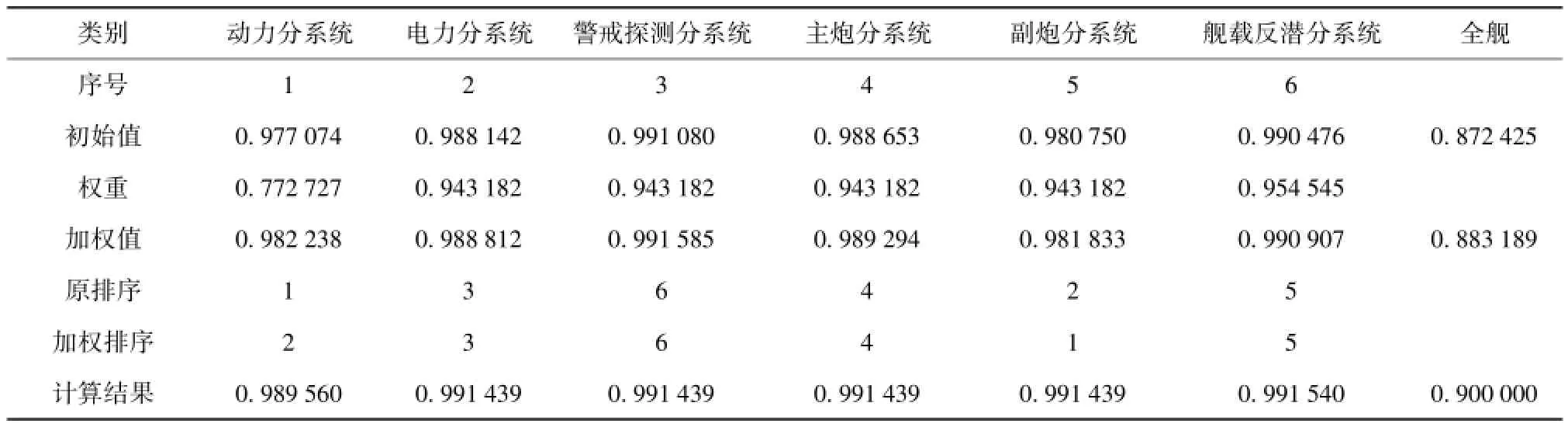
表1　由全舰到各分系统的优化与协调数据和计算结果Tab.1 Optimized and coordinated availabilities of whole ship and subsystems

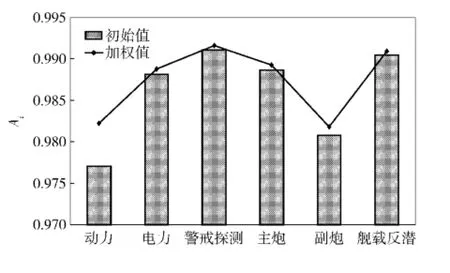
图4　加权处理对分系统改进顺序的影响Fig.4 Influences of weights on improvement sequence of subsystems

根据优化计算的结果，综合考虑初值和改进难度系数后，加权排序为1～6的分系统可用度都需要有一定程度的提高，改进幅度依序为：动力分系统→副炮分系统→电力分系统→主炮分系统→舰载反潜分系统→警戒探测分系统。各分系统改进幅度如图5所示。

图5　全舰各分系统可用度指标的改进幅度Fig.5 Improvement of various subsystem availabilities

可以预计，如果要求值At≤0.872 425，则全舰所有分系统的指标均无需改变；反之，如果在现有水平基础上，继续提高At值，将会对更多的分系统依序提出相应的改进要求。将以上数据分别代入Matlab程序，验证了这些分析结论。

全舰各分系统可用度初始值、加权值和计算结果如图6所示。

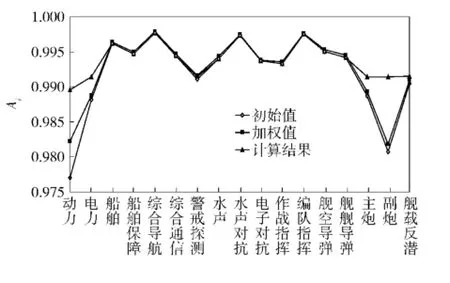
图6　全舰各分系统可用度指标的对照结果Fig.6 Contrast results of various subsystem availabilities

分析可知，对于各分系统Ai而言，有At≤Ai＜1 （i=1，2，…，17）成立，据此计算可得其标准差的最大值为σmax=0.05，原始数据和优化计算结果的标准差分别为σr=0.005 549，σo=0.002 374.借助于均值和方差的概念，全舰各分系统可用度的协调一致性即协调度指标可以定义为Sc=1-σ/σmax，则显然有0≤Sc≤1.按此计算可得，优化前后分系统级指标协调度的改进幅度为6.36%，改进效果明显。

5.3由各分系统向所属设备的优化与协调计算

由各分系统向所属设备的优化与协调计算比上一部分要复杂一些，为了实现分系统的Ai，依序对各设备的Aij改进提出要求。而为了实现Aij的改进要求，各设备的MTB″和MTTR就必须单独或同时调整，调整的方式分别对应着以上各个扩展算法。

为了展示算法的效果和在各分系统的应用情况，以动力分系统为例，采用部分算法和策略进行优化计算。

5.3.1动力分系统的计算结果与分析

采用原始数据（表2第1行）进行计算可知，无论采用哪种算法，该分系统均无法达到表1所规定的指标。表明动力分系统现有设备的可靠性和维修性指标过低，各指标取到上限（可靠性指标取到最大值，维修性指标取到最小值）都无法满足要求，已明显成为全舰各分系统的短板。因此，对该分系统所属设备的可靠性和维修性指标的上限进行调整（数据略），计算结果如表2所示。

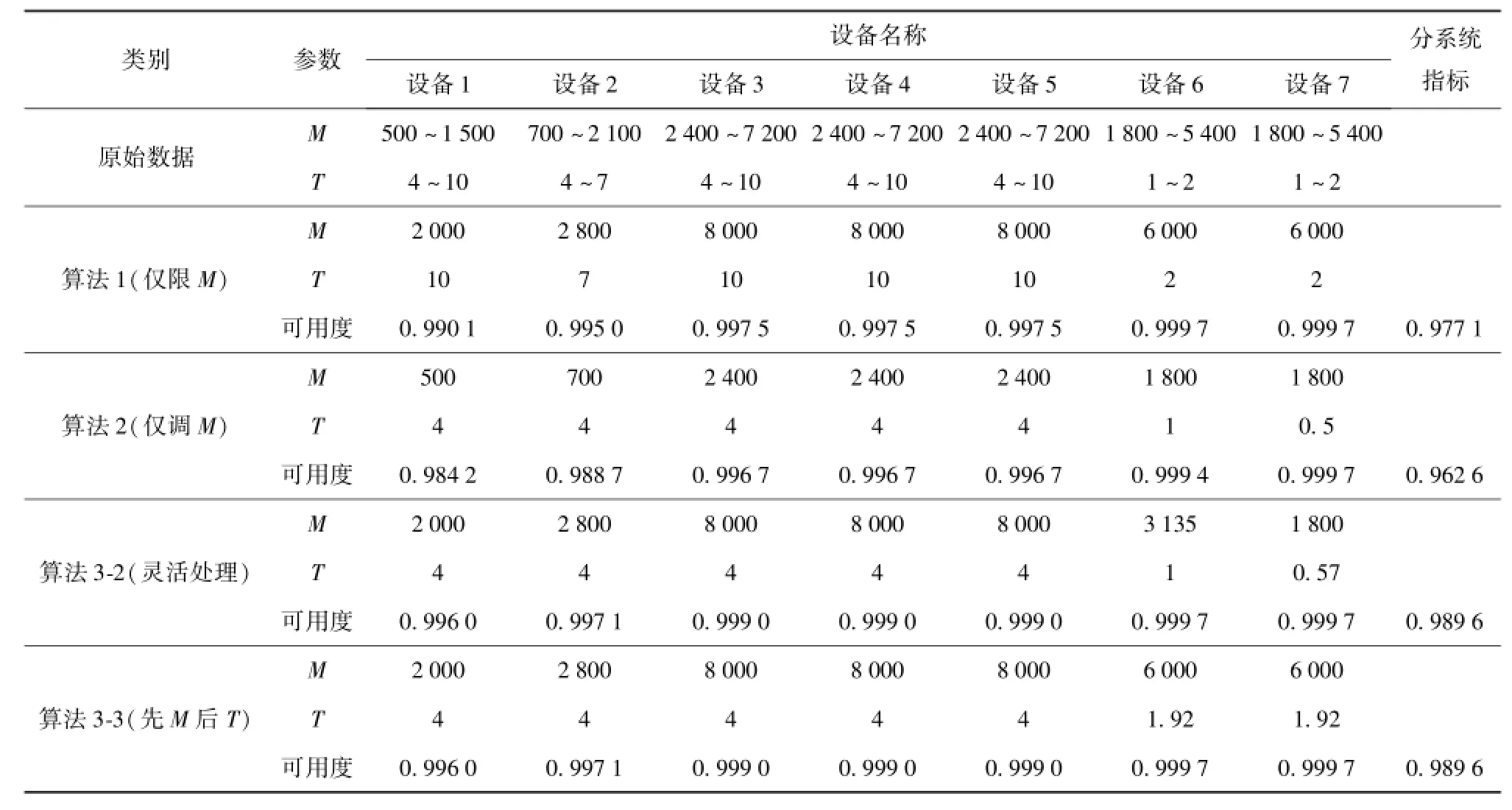
表2　动力分系统所属设备的可靠性维修性指标的优化结果Tab.2 Optimized results of reliability and maintainability of equipment in propulsion subsystem

对比输入数据并分析计算结果可知，即便采用修改后的指标上下限，为了满足全舰各分系统间的总体协调要求，单独实施扩展算法1和扩展算法2，且分别导致设备级的可靠性指标达到上限，维修性指标达到下限，而分系统级可用度指标仍未达标。反映对于动力分系统而言，扩展指标的上下限后，单独实施可靠性或维修性改进工程效果仍然不够理想。

而算法3的两种形式均可达到目标，但是即便采用算法3-2和3-3，也将导致大部分可靠性、维修性指标达到上下限值，该分系统各设备采用算法3-2的计算结果如图7（可靠性）、图8（维修性）所示。由图7、图8可知，对于该分系统而言，必须实施可靠性和维修性综合改进工程，才能达到预期效果，而且其工作难度很大。与此同时，算法3的两种形式表明，在开展可靠性和维修性综合工程时，具体采用哪种形式（策略）可以根据工程实际灵活选择。

由图7、图8可知，该分系统中，应作为可靠性指标改进重点的设备是设备1～设备5，维修性指标改进重点的设备是设备1～设备6，其数量多，改进难度大，可见该分系统是全舰可靠性和维修性工程的重点。

5.3.2其他各分系统的计算结果与分析

根据各分系统的输入数据，采用本文算法对表1其他5个分系统都进行了优化计算和分析，得到了如下结论：1）5个分系统均无需调整指标上下限；2）电力分系统、警戒探测分系统、主炮和副炮分系统单独采用算法1、算法2均不能满足要求，舰载反潜分系统采用算法1可以、采用算法2不能满足要求；3）5个分系统采用算法3-1、3-2均可满足要求，表3给出了部分细节，其中工作难度是根据计算结果主观判定的。

5.3.3导出信息和扩展研究的设想

在以上优化计算和分析的基础上，还可以对全舰各分系统进行比较和分类，对各分系统需要分类重点关注的设备及其特点进行分析，从而为装备总体研制提供理论依据和进一步的决策信息。

图7　采用算法3-2的可靠性指标的相对值和绝对值Fig.7 Relative and absolute numerical values of reliability obtained from algorithm No.3-2

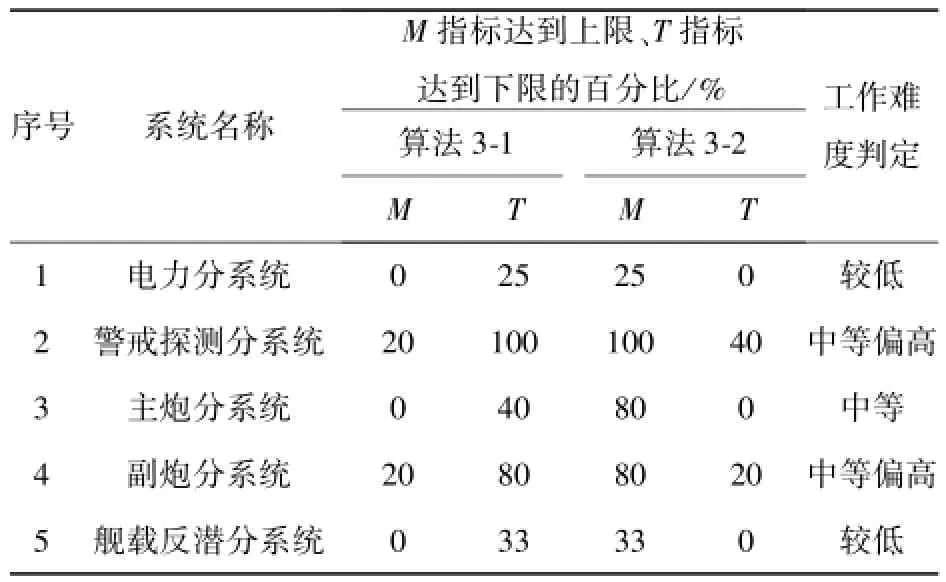
表3　其他分系统所属设备的优化结果相关信息Tab.3 Optimized results of equipment in other subsystems

以上为针对同一个总体级指标，即At不变所得到的结论。以固定的间隔变换不同的At初值要求水平，对于装备所属的分系统，以及各分系统所属设备，反复进行类似的计算和分析，就可以得到一个装备所属的各分系统设备可靠性和维修性指标的谱系，分析其间的相互关系和趋势，还可以得到更多的有用信息。

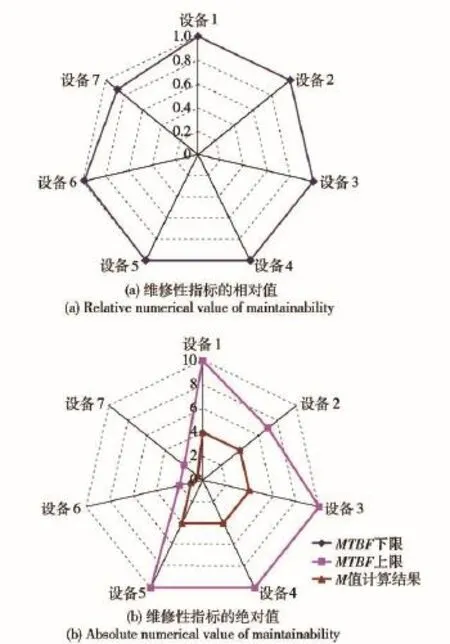
图8　采用算法3-2的维修性指标的相对值和绝对值Fig.8 Relative and absolute numerical values of maintainability obtained from algorithm No.3-2

6　结论

本文对于大型复杂武器系统以海军舰船为例，通过对其使用特点及其结构组成的分析，在确定了各分系统可用度指标协调优化基本原理的基础上，根据指标传递和优化原理，明确了总体-分系统-设备指标的关联关系，在现有研究的基础上，给出了在规定的总体可用度条件下，确定各分系统所属设备可靠性和维修性指标的模型和优化方法。算例和分析表明，本文的方法能够有效解决大型复杂武器系统可靠性和维修性指标的总体优化问题，已应用于某型舰的总体可靠性和维修性工程研制中，效果十分理想。为实现装备各分系统之间指标的相互协调，以最小的代价实现和改进总体可用度指标，使装备各分系统所属设备的可靠性和维修性这些看似离散的指标构成一个整体，提供了理论依据和实现方法。对于该问题的深化研究和该方法的进一步推广应用，将是本文下一步的努力方向。

参考文献（References）

［1］ 韩坤，何成铭，刘维维，等.以系统效能为目标的装甲车辆可靠性、维修性、保障性和测试性权衡分析［J］.兵工学报，2014，35（2）：268-272. HAN Kun，HE Cheng-ming，LIU Wei-wei，et al.Trade-off analysis of reliability/maintainability/supportability/testability of armored vehicle based on system effectiveness［J］.Acta Armamentarii，2014，35（2）：268-272.（in Chinese）

［2］ 梁丰，张志利，高钦和，等.大型武器装备故障建模与仿真技术研究［J］.系统仿真学报，2011，23（1）：42-46. LIANG Feng，ZHANG Zhi-li，GAO Qin-he，et al.Research on fault modeling and simulation technology of large-scale armament equipment［J］.Journal of System Simulation，2011，23（1）：42-46.（in Chinese）

［3］ Charles E，Kondo A.Availability allocation to repairable systems with genetic algorithms：a multi-objective formulation［J］.Reliability Engineering and System Safety，2003，82（3）：319-330.

［4］ 毛德军，李庆民，张志华.装备可用度为中心的保障方案优化方法［J］.兵工学报，2011，32（5）：636-640. MAO De-jun，LI Qing-min，ZHANG Zhi-hua.An optimizing method for availability-centric equipment support plan［J］.Acta Armamentarii，2011，32（5）：636-640.（in Chinese）

［5］ Kobren，B.Product support and human capital：essential ingredients for optimizing system readiness，availability，and life cycle costs，ADA564401［R］.FT Belvoir，VA：Defense Acquisition University，2011.

［6］ 罗祎，阮旻智，李庆民.多级维修供应下不完全串件系统可用度评估［J］.系统工程与电子技术，2012，34（6）：1182-1186. LUO Yi，RUAN Min-zhi，LI Qing-min.Evaluation of availability for incomplete cannibalization systems under multi-echelon maintenance supply［J］.Systems Engineering and Electronics，2012，34（6）：1182-1186.（in Chinese）

［7］ 谢宗仁.基于影响因子的舰船总体效能优化研究［D］.武汉：海军工程大学，2014. XIE Zong-ren.The optimization research on the ship's effectiveness based on influence factors［D］.Wuhan：Naval University of Engineering，2014.（in Chinese）

［8］ 吕建伟，余鹏，刘中华，等.舰船总体任务可靠性的多阶段工程分析法［J］.中国造船，2011，52（3）：182-189. LYU Jian-wei，YU Peng，LIU Zhong-hua，et al.Phased engineering analysis approach of whole ship's mission reliability［J］.Shipbuilding of China，2011，52（3）：182-189.（in Chinese）

［9］ 毛炳祥，白桦，程文鑫.系统战备完好性分析计算与检测［M］.北京：国防工业出版社，2012. MAO Bing-xiang，BAI Hua，CHENG Wen-xin.System operational readiness analysis，computation and detection［M］.Beijing：National Defense Industry Press，2012.（in Chinese）

［10］ 林武强.装备RMS要求论证方法研究［D］.北京：北京航空航天大学，2004. LIN Wu-qiang.Study on demonstration methods of RMS requirements for equipment［D］.Beijing：Beihang University，2004. （in Chinese）

中图分类号：TJ02；U674.7

文献标志码：A

文章编号：1000-1093（2016）06-1144-09

DOI：10.3969/j.issn.1000-1093.2016.06.025

收稿日期：2015-12-10

基金项目：国家自然科学基金项目（71401171）；总装备部预先研究基金项目（9140A19030214JB11273）；军队院校2110工程3期建设基金项目（4142D4557）

作者简介：吕建伟（1962—），男，教授，博士生导师。E-mail：l2015wh@163.com

Overall Optimization of Reliability and Maintainability of Major Weapon System

LYU Jian-wei，XU Yi-fan，XIE Zong-ren
（Department of Management Science，Naval Univiversity of Engineering，Wuhan 430033，Hubei，China）

Abstract：The availability is an important part of weapon system effectiveness，and also the prerequisite for achieving the conventional technical performance.By the discussion of the hierarchical structure of weapon system and the basic formulas for its availability，a fundamental principle of coordinating and improving the availability indicators among different subsystems is proposed based on mathematical analysis.The effect of improving difficulty of subsystem availability on improving order is discussed according to engineering practice.And an optimization method and its algorithm are designed for subsystem availability，equipment-level reliability and maintainability.Furthermore，based on a type of navy vessel，the feasibility and validity of the proposed algorithm are verified by Matlab programming.A theoretical basis and implementation approach are provided to obtain and improve the total availability with minimum cost，and take different equipment reliability and maintainability of different subsystems as an integration indicator.

Key words：ordnance science and technology；weapon system；availability；subsystem and equipment；reliability；maintainability；overall optimization