势能的特点和应用

◇　江苏　吴小兵



非常道

势能的特点和应用

◇江苏吴小兵

如果一个力做功跟物体的运动过程无关,只跟物体的初末位置有关,那么这个力就被称为保守力.每一个保守力都对应着一种势能,势能大小只跟位置有关.高中阶段我们学过不少势能，如重力势能、电势能、分子势能等．我们分析重力势能、电势能、分子势能和它们对应的保守力关系时会发现，在一个过程中势能的减少量跟这个保守力做的功是相等的．实际上不止这3种势能,所有的势能都有这一特点．高考时不仅会考我们高中阶段学过的势能,还有可能出现一些从来没学过的势能,但是只要我们理解了势能跟对应的保守力做功之间的关系，就能顺利解决问题．

1万有引力势能

由于万有引力对物体做功跟物体的运动过程无关，只跟物体的初末位置有关,所以我们可以定义一个跟万有引力对应的势能——万有引力势能．我们学过重力势能,实际上重力势能是万有引力势能在地球表面附近的近似表示．

(1)、(2) 略.

(3) 若万有引力常量为G,中心天体的质量为m0,质量为m的物体距中心天体r时具有的引力势能为Ep=-Gm0m/r(以无穷远处势能为0)．

① 求出第二宇宙速度的值;

② 若把地球绕太阳公转的轨道近似认为是圆,且不计其他星体对飞行物体的作用力,地球的公转速度为29.8 km·s-1,求第三宇宙速度．

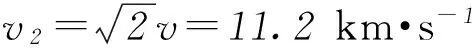
2弹性势能

虽然在学习机械能时我们提到了弹性势能,但弹性势能的计算公式并不要求我们掌握．在高考中曾多次出现弹性势能有关的计算,这时我们只能根据弹性势能跟弹力做功的关系来解决．

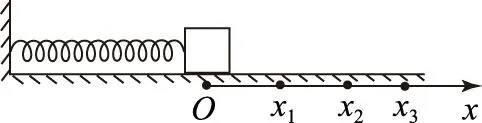
图1

(1) 请画出F随x变化的示意图,并根据F-x的图象求物块沿x轴从O点运动到位置x的过程中弹力所做的功?

(2) ① 求弹力所做的功?并据此求弹性势能的变化量;

② 求滑动摩擦力所做的功;并与弹力做功比较,说明为什么不存在与摩擦力对应的“摩擦力势能”的概念.

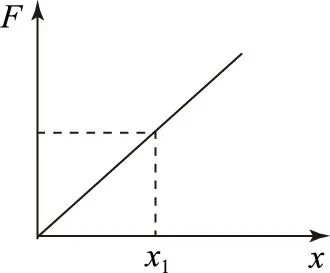
图2

W=-kx2/2.

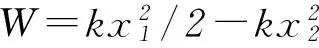
② 在此过程中摩擦力做功Wf=-μmg(2x3-x2-x1)．我们可以看出摩擦力做功与路程成正比,而非像弹簧弹力做功一样与路径无关,而只与初末位置有关,所以无“摩擦力势能”的概念．

3分子势能

学习热学时我们知道由于分子间存在相互作用的引力和斥力,引力和斥力做功只与它们的初末位置有关,因此存在跟分子力相对应的分子势能．在一个过程中分子势能的减少量也等于分子力所做的功．

图3

A在r>r0阶段,F做正功,分子动能增加,势能减小;

B在r

C在r=r0时,分子势能最小,动能最大;

D在r=r0时,分子势能为0;

E分子动能和势能之和在整个过程中不变

势能虽然是根据保守力做功定义的,但势能并不是功．它跟功的含义有很大的区别,它又跟功有着很重要的联系(在一个过程中势能的减少量跟这个保守力做的功是相等的),抓住这个联系去分析问题,我们往往能够化繁为简，快速解题．

(作者单位：江苏省口岸中学)