基于“变易表”的整合学习
——以等差、等比数列学习为例
2016-07-28广东陈雪玲
◇ 广东 陈雪玲
非常道
基于“变易表”的整合学习
——以等差、等比数列学习为例
◇广东陈雪玲
概念的学习是高中数学学习的核心内容,在学习概念的过程中,我们可以通过变易表来进行辨析学习,变易表能带出4个主要学习功能:对照、区分、类合和融合,每种功能关注学习内容不同的方面,正是这4个功能,让我们可以对概念进行整合学习.这样学习,既可以关注到概念的主要特征,又可以和相邻概念进行区分.下面我以等差数列和等比数列的整合学习为例,介绍基于变易表的整合学习,以帮助大家掌握学习内容.
1利用对照,辨析概念
通过相互“对照”可以区分出不同的、相异的事物.数学概念必定有与之相关的邻近概念, 因此学习中要以已掌握的知识为基础, 从邻近概念出发, 探求新旧概念之间的区别和联系,这样有助于掌握概念的本质, 提高对数学理论整体性与严密性地把握.
利用变易表的对照功能,把等差、等比数列的概念联系起来.
等差数列的定义:如果一个数列从第2项起(条件A),每一项与它的前一项的差(条件B)都等于同一个常数(条件C),这个数列叫做等差数列.这个常数叫做数列的公差,用d表示.
在等差数列的定义中,有3个重要特征,我们把它们分别记为条件A、B、C,为了更好地辨析概念,设计了下列变易表(表1~3).

表1


表2


表3

进一步分析表3的例子,从第2项起,每一项与前一项的比都等于同一个常数3,从而引入等比数列概念,得到等比数列的概念,如表4.

表4
通过变易表,同时进行2个概念的学习,能很好的对照2个概念的条件A、C是相同的,等差数列中的条件B由差改为比,就成了等比数列.等差数列关键特征是“差”,等比数列关键特征是“比”.
同样,2个概念学习后,对等差中项和等比中项2个概念也是通过变易表进行对比学习,如表5.

表5
通过对概念的条件或特征进行变易,从而得到新的知识,通过对照可以较快地接受新知识.有对照才有鉴别.用对比方法找出容易混淆概念的异同点,有助于区分概念,获取准确、明晰的认识.
2利用区分,突显关键特征的作用
利用变易表体现出的对照效果,能把注意力聚焦于关键特征上,也有助于“区分”相关概念.如上面,利用对照得到等差、等比数列的概念后, 还要根据等差数列关键特征“差”,等比数列关键特征“比”推导2个数列的通项公式.而变易表中的区分主要就是把关键特征显现出来,探究关键特征的作用.
2个数列通项公式的推导,在变易表的体现是由主要特征引起的思想方法的变易.
一般地,等差数列{an}中,首项是a1,公差是d,将an用a1、n、d表示,有a2-a1=d,a3-a2=d,…,an-an-1=d,…(条件A)
将上面n-1个式子相加(条件B)有:an=a1+(n-1)d,以上采用的方法为累加法.
条件A、B都是由等差数列的关键特征“差”决定,从而引导学生认识等比数列的关键特征为“比”,则条件A、B如何变化?

表6

新接触一个概念、定理或性质,往往对其中的条件不是很熟悉,通过对条件进行变易,清楚其关键特征,并通过区分设计变易表探究关键特征的作用,从而加深对整个概念的理解.
在学习过程中,我们发现同学们易从等差数列通项公式推导方法“区分”出等比数列通项公式推导方法,而且对累加法和累乘法也有了对照的认识.利用对照、区分,把2个数列的概念、通项公式整合在一起,突出2个数列的特征.
3利用类合,总结规律
“类合”是在区分后的高层次的对照,用于查对分辨出来的数学规律是否有普遍性.学生对各个数学概念、定理等有了认识,但是缺乏的是知识间的对照和类合,所以应该通过变易表,发挥类合功能,对知识规律进行总结和应用.通过变易表,从变化中审辨出不变的规律.

(1)a1+a9=a3+a7. (2)a2+a8=a4+a6.
(3) 2a5=a1+a9.(4)a1+a2+a7=a4+a6.
从而得到性质:若m+n=p+q(m、n、p、q∈N+),则am+an=ap+aq,若m+n=2p,则am+an=2ap.证明结论后,进一步把等差、等比进行类合,发现性质,总结规律,因此给出表7.

表7
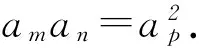

(2)等比数列{an}中,a3+a8+a13=13,a3a8a13=27,求{an}的通项公式.

“类合”可以形成一种更高层次的思维方法.题目的变易不是几个独立数学问题的简单组合,而是注重题目之间的内在联系,这些问题的解决能启示一种数学规律、能引导与启发大家掌握这种规律.通过变易表的类合,让大家更清晰这2个数列的性质及运用.
4利用融合,提升思维
“融合”是把不同的关键特征对照起来,找出不变的整体意义.融合要注意事物、概念或现象同时变化的几个方面,以及这些方面与作为整体的学习内容之间的关系.证明数列为等差数列或等比数列,这类题目极为常见,也非常重要,但大家往往掌握不好,原因主要是没有紧扣定义.在此利用变易表“融合”的功能,将课本证明等差、等比数列的题目进行整合,让大家掌握证明的方法.

这是一道证明等差数列的题目,只要找到an-an-1为常数(n>1)即可.因为an-an-1=pn+q-[p(n-1)+q]=p(n>1)显然为等差数列.为了让学生更好地掌握证明,设计出表8.

表8

此题只要找出(pan+qbn)-(pan-1+qbn-1)=p(an-an-1)+q(bn-bn-1)=pd1+qd2为常数(n>1)即可.
同样,在等比数列证明中,给出下例.



表9
利用上述各例,让大家抓住等差数列和等比数列的定义来进行证明,思维方法是相通的.通过融合的学习功能及变易表,找到概念间不变的东西,并融合到解题中,理解这些“变中不变”的关系之后,大家再解决相关的题目时,方能游刃有余、从容不迫,达到以不变应万变的能力要求.
以变易进行学习,有助于审辨学习内容的关键特征,构建及表达出恒成立的数学规律、整合教学,从而提高学习质量.
(作者单位:广东省广州市第八十中学)
