三角函数的特性及应用
2016-07-28酒泉市一中甘肃酒泉735000
田 麟(酒泉市一中,甘肃 酒泉 735000)
三角函数的特性及应用
田 麟
(酒泉市一中,甘肃 酒泉 735000)
摘 要:本文结合三角函数综合题常见题型,对三角函数单调性、周期性、最值;三角函数图像与图像变换;三角函数图像与解析式的互相转化及三角函数与相关知识的融合题等题型的考查特点,出题方式、注意问题进行了具体分析探究,并提出对应备考方法与答题策略。
关键词:三角函数;单调性;周期;最值
三角函数综合题作为高考考查的热点与高频考点,经过多年高考的磨砺整合,目前基本形成了内容稳定、题量稳定、分值稳定和难度适中四大特征[1]。如何在高考中轻松准确的解答三角函数题呢?笔者结合经验,为大家的备考复习提供一点思路。
1 考点再现
考点一:三角函数单调性、周期性、最值
【方法与技巧】
①将三角函数化归为f(x)=Asin (ωx+φ)的形式。②结合三角函数的图像,运用整体代入的基本思想求三角函数的单调性,最值与周期。
例1 已知函数f(x)=(sin2x+cos2x)2 -2sin2 2x 。
(1)求f(x)的最小正周期;
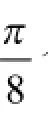
解:因为f(x)=(sin2x+cos2x)2-2sin2 2x

考点二:三角函数图像与图像变换
【方法与技巧】
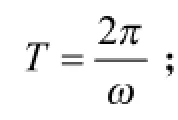
三角函数平移:一般地,函数y=sin (ωx+φ)的图像,可以看作把曲线y=sinx的图像上所有点向左(当0φ>时)或向右(当0φ< 时平移个单位长度而得到的;或者看作把曲线sinyxω=上所有点向左(当0φ> 时)或向右(当0φ<时)平移个单位长度而得到的。
考点三:三角函数图像与解析式的互相转化
【方法与技巧】
根据y=Asin(ωx+φ)+K 的图像求其解析式的问题,主要从以下四个方面来考虑:
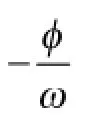
考点四:知识交汇点处的三角问题
(1)三角函数与向量
【方法与技巧】
①由向量的运算性质将问题转化为三角函数关系式,将关系式化归为y=Asin(2x+φ)+k形式,再结合三角函数的图像性质求解单调性、周期、最值等相应问题。②求最值时由自变量x的范围,转化出ωx+φ的范围,在范围内借助图像找最值。
例2 已知向量a=(cosωx-sinωx,sin ωx ),设函数f(x)=a· b+λ(x∈R)的图像关于直线x=π对称,其中ω、λ为常数,且
(1)求函数f(x)的最小正周期;
(2)三角函数与解三角形
【方法与技巧】
①应用三角公式中的二倍角公式、两角和、差公式及辅助角公式化简转化。
②解三角形时应用正、余弦定理进行边角转化,一般边为一次时用正弦定理边角转化,边为二次时用余弦定理转化。
2 精髓解读
(1)把“ωx+φ(ω>0)”视为一个“整体”。(2)A<0时,所列不等式的方向与y=sin x(x∈R),y=cos x( x∈R)的单调区间对应的不等式方向要相反。(3)求函数f(x)=Asin(2x+φ)的单调区间,只有当ω>0时,才可整体代入并求其解,当ω<0时,需把ω的符号化为正值后求解。(4)求三角函数的最值时,要注意自变量x的范围对最值的影响。(5)平移转换时分清是由y=sinx的图像平移转化得到的,还是由y=sinωx的图像平移转化得到的。
3 方法导引
(1)发现差异:观察角、函数运算间的差异,角相同时则变形,角不同则化角,即观察角之间是否存在和、差、二倍关系。
(2)寻找联系:运用相关公式,找出差异之间的内在联系,即观察已知与已知之间,已知与未知之间的相互关系,寻找出内在联系。
(3)合理转化:选择恰当的公式,促使差异的转化,角相同则应用常见公式:
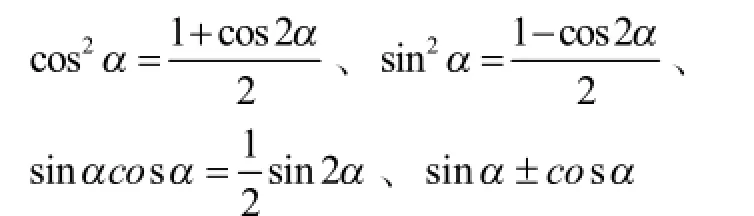

化归;角不相同同,则用和角公式、差角公式、二倍角公式化归为 f(x)=Asin (ωx+φ),再求解。
参考文献:
[1]梁志芳.学生学习三角函数的调查研究[M].石家庄: 河北师范大学,2011.
[2]符白陵.高中数学三角函数的教学策略研究[M].海口: 海南师范大学,2014.
(责任编辑:吴 芳)
中图分类号:O1-645
文献标识码:A
doi:10.3969/j.issn.1672-7304.2016.01.059
文章编号:1672–7304(2016)01–0125–02
作者简介:田 麟(1973-), 男,甘肃酒泉人, 一级教师,研究方向:数学教学。
The characteristic and application of trigonometric function
TIAN Lin
(One in Jiuquan, Jiuquan Gansu 735000)
Abstract:Combining with comprehensive topic common mould, trigonometric function examination characteristic, mode, draw attention question has carried on the concrete analysis, and put forward the corresponding test methods and problem solving strategies.
Key words:Trigonometric function; monotone; cycle; the most value
