无限区间上均布变量概率计算方法研究

刘宝慧（青海大学，青海 西宁 810016）



无限区间上均布变量概率计算方法研究

刘宝慧
（青海大学，青海 西宁 810016）

摘 要：给出了随机变量X在无限区间（0，∞ ）、（-∞，0）、（-∞，+∞）上服从广义均匀分布的概念及计算概率的方法。

关键词：均匀分布；极限分布；广义均匀分布

1　无限区间Θ上广义均匀分布的概念

关于随机变量X的“均匀”分布问题，因X的取值范围不同而形成了不同的定义方法。

当随机变量X在有限个值xi，i= 1，2，…，n 上“均匀”分布时，我们用X在各个值上的概率相等来定义均匀分布，即：

当随机变量X在有限区间（a，b）上“均匀”分布时，因为在（a，b）上连续分布的随机变量都有P（X=x）=0，x∈（a，b），所以不能用X取值的概率相等来定义有限区间（a，b）上的均匀分布。此时，我们用X在有限区间（a，b）上取值的密度相等来定义X在有限区间（a，b）上的均匀分布，即定义密度为：

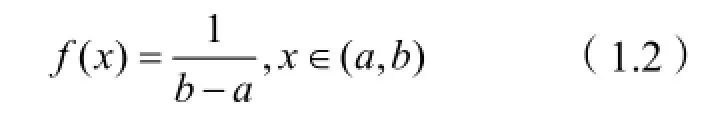
设Θ为无限区间（0，∞）或（-∞ ，0）或（-∞，+∞），当随机变量X在无限区间Θ上“均匀”分布时，如何定义X在无限区间Θ上均匀分布？

定义 1.1：设随机变量X取值范围为无限区间Θ，Θ为（0，∞）或（-∞，0）或（-∞，+∞），π（x）（ x∈Θ）是随机变量X在x值的概率分布，若π（x）满足条件：

（1）π（x）≥0，

（2）对∀x1，x2∈Θ且x1≠x2，有π（x1）=π（x2），

则称随机变量X在无限区间Θ上服从广义均匀分布。称π（x）为X在无限区间Θ上的广义均匀分布密度。我们认为当随机变量X在无限区间Θ上“均匀”分布时，X没有大于0的密度。用反证法来证明：若X在无限区间Θ上“均匀”分布，且有大于0的密度0c≻，则必然事件Ω概率

这显然与必然事件的概率P（Ω）=1 相矛盾。

正因为当X在不同的无限区间上“均匀”分布时，都没有大于0的密度，故不能用密度来定义无限区间上的“均匀”分布，而文［4］仍沿用密度来定义无限区间上的“均匀”分布，因而在实际计算中产生了许多矛盾。

本文中，我们用随机变量X在无限区间Θ上的“均匀”分布，称之为X在无限区间Θ上的广义均匀分布，并给出了在这种分布下如何计算概率的方法。

2　无限区间（0，∞）上的广义均匀分布

当随机变量X在无限区间（0，∞ ）上的“均匀”分布时，我们给出以下定义。

定义 2.1：设随机变量X的取值范围为无限区间（0，∞），且设X在任一有限区间（0，a）（a≻0，a∈R）上服从均匀分布，当a→∞时，称X在（0，a）上的均匀分布的极限为X在无限区间（0，∞）上的广义均匀分布。

当随机变量X在无限区间（0，∞）上服从广义均匀分布时，为了计算概率，我们给出了定理。

定理 2.1：设随机变量X的取值范围为无限区间（0 ，∞）服从广义均匀分布，则有：

（1）设 b ，c∈R，且（b，c）⊆（0，∞），有

P（x∈（b，c））=0 P（x∈［b，c））=0

P（x∈（b，c］）=0 P（x∈［b，c］）=0 （2.1）

设b∈R且b≥0，有P（x∈（b，∞））=1；（3）当b∈（0，∞）时，有P（X=b）=0；当x∈（0，∞）时，f（ x）为X的密度函数，则有f（ x）=0。

3　无限区间（-∞，0）上的广义均匀分布

当随机变量X在无限区间（-∞，0）上“均匀”分布时。我们给出如下定义。

定义 3.1：设随机变量X的取值范围为无限区间（-∞，0），且设X在任一有限区间（a，0）（a≺0）上服从均匀分布，当a→-∞时，称X在（a，0）上的均匀分布的极限分布为X在无限区间（ -∞，0）上的广义均匀分布。当随机变量X在无限区间（-∞，0）上服从广义均与分布时，为了计算概率，我们给出以下定理。

定理3.1：设随机变量X在无限区间（- ∞，0）上服从广义均匀分布，则有

（1）设 b ，c∈R且（b， c⊆（-∞ ，0）），有

P（ x∈（b，c））=0P（x∈［b，c））=0

P（ x∈（b，c］）=0P（x∈［b，c］）=0 （3.1）

（2）设b∈R且b≤0，有

P（x∈（-∞，b））=1，x为X的取值 （3.2）

（3）当b∈（-∞ ，0）时，有

P（X=b）=0 （3.3）

（4）当x∈（-∞，0），f（x）为X的密度，则有

f（x）=0 （3.4）

4　无限区间（-∞，∞）上的广义均匀分布

当随机变量X在无限区间（-∞，∞）上“均匀”分布时定义如下：

定义 4.1：设随机变量X的取值范围为无限区间（-∞，∞），且X在任一有限区间（-a，a）上服从均匀分布，当a→∞时，称X在（-a，a）上均匀分布的极限分布为X在无限区间（-∞，∞）上的广义均匀分布。

定理 4.1：设随机变量X在无限区间（-∞，∞）上服从广义均匀分布，则有

（1）设b，c∈R，b≺c，（b，c）⊆（-∞，∞），有

P（x∈（b，c））=0P（x∈［b，c））=0

P（x∈（b，c］）=0P（x∈［b，c］）=0（4.1）其中x是X的取值。

（3）设b∈R，有

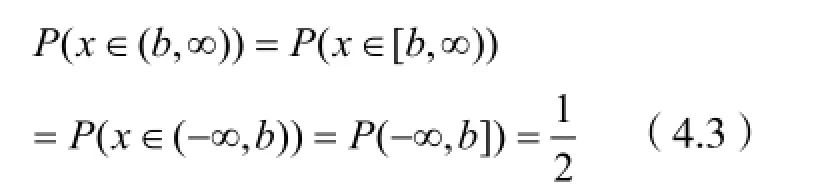
（4）P（x∈（-∞，∞））=1 （4.4）

（5）当b∈（-∞，∞）时，有

P（X=b）=0 （4.5）

（2）P（x ∈（0，∞）⊆（-∞，∞））

P（x∈（-∞，0）⊆（-∞，∞））

同理可证（3）的另外三个等式成立。

（4）当X在（-∞，∞）上服从广义均匀分布时，因X在（-∞，∞）上取值为必然事件Ω，故

P（x∈（-∞，∞））=P（ x ∈Ω）=1

因0≤P（X=b）≤P（b-1≤x≤b+1）=0；所以，当b∈（-∞，∞）时，有P（X=b）=0。证毕。

参考文献：

［1］茆诗松，程依明，濮晓龙.概率与数理统计［M］.北京: 高等教育出版社，2005.

［2］茆诗松，汤银才.贝叶斯统计［M］.北京:中国统计出版社，2013.

（责任编辑：张时玮）

中图分类号：TL329+.2

文献标识码：A

doi:10.3969/j.issn.1672-7304.2016.01.049

文章编号：1672–7304（2016）01–0103–02

* 基金项目：青海大学中青年科研基金项目（2014-QSY-1）。

作者简介：刘宝慧（1972-），女，河北保定人，讲师，研究方向：经济统计。

On the infinite interval uniform variable probability calculation method

LIU Bao-hui
（Qinghai University， Xining Qinghai 810016）

Abstract:Offering the concept and probability calculation method that how random variable X obeys extended even distribution in the infinite interva（0，∞）、（-∞，0）、（-∞，∞）.

Keywords:Even distribution； limiting distribution； extended even distribution