数据和导频通道的功率加权联合捕获算法*

田　丰，唐小妹，欧　钢

(国防科技大学 电子科学与工程学院， 湖南 长沙 410073)



数据和导频通道的功率加权联合捕获算法*

田丰，唐小妹，欧钢

(国防科技大学 电子科学与工程学院， 湖南 长沙 410073)

摘要：下一代全球导航卫星系统将采用数据和导频通道功率不等的调制方式，而传统算法多采用数据和导频通道的等权重加权联合进行捕获。当二者功率不相等时，等权重加权联合不能获得最优的捕获性能。因此提出功率加权联合的改进捕获算法，在数据和导频通道的功率分配不等的情况下，进行不同加权系数的联合捕获，并且利用最小二乘的方法进行最优加权系数的拟合估计。利用捕获判决量的特征函数推导检测和虚警概率。仿真实验验证了当数据和导频功率比为1 ∶3、检测概率为0.8、虚警概率为10-3时，所提出的改进算法能提升0.4 dB的捕获灵敏度。

关键词：非相干；联合捕获；导频通道；加权系数；特征函数

新信号体制设计提出了数据和导频通道功率不相等的信号调制方式，并被全球定位系统(Global Positioning System，GPS)采用，其中GPS L1C信号的数据通道L1CD和导频通道L1CP功率比为1 ∶3[1]。目前数据和导频通道联合捕获算法主要基于二者功率一致的情况进行设计和分析，而分析的结论不能通过简单推导应用到二者功率不等的情况。例如，文献[2-4]对数据和导频功率相等时的非相干、差分以及半相干联合捕获算法的检测概率和虚警概率进行了推导并获得了解析表达式；文献[5]对各种联合捕获算法的后累积性能进行了理论推导和仿真分析，但都没有对数据和导频功率不相等的情况进行分析；文献[6]提出了L1/L2频点间加权联合捕获算法，但是并没有对加权系数的影响进行分析；文献[7]给出了GPS的L1C和L1C/A联合捕获算法，并提出了使得噪声最小的加权联合捕获算法，此加权系数主要针对相干联合捕获，并且没有给出性能分析的理论推导。

田丰等针对数据和导频通道功率不相等的情况，对非相干联合捕获算法的性能进行分析，并在此基础上提出了功率加权联合捕获算法。该算法根据数据和导频通道的功率分配情况，进行不同加权系数的联合捕获，提高捕获的性能。

1功率加权联合捕获算法

1.1信号模型

具有数据和导频通道的导航信号经过天线接收、低噪放大、混频、滤波以及模拟数字转换器(Analog to Digital Converter, ADC)等一系列处理之后，可以采用式(1)信号模型表示。

(1)

其中：rIF表示接收的中频信号；CD和CP分别表示数据和导频的信号功率；Ts表示ADC采样周期；F0为包含多普勒频率的中频频率；φ0为接收信号的初始相位；τ0为伪码相位传播时延；ηIF为功率谱密度为N0的窄带高斯白噪声采样；eD和eP分别表示数据和导频调制的信号波形或电文符号。它们可以表示为：

(2)

其中：d表示导航电文；sb表示副载波；sD和sP分别表示为数据和导频通道用于位同步的次级码；cD和cP分别表示为数据和导频通道的主码。对于没有调制副载波的信号，可以令sb(t) = 1。

信号捕获是对多普勒频率和伪码传播时延的二维搜索。接收的中频信号首先与本地生成的载波信号相乘，进行去载波多普勒的处理；然后与本地生成的伪码信号相乘后，输入到积分器进行累积，获得相干积分值。图1为单个通道的捕获相关值生成的结构图，生成的相关值为：

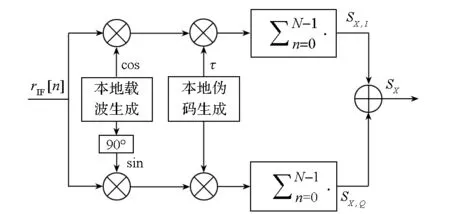
图1　单通道捕获相关值生成框图Fig.1　Coherent correlation structure of single channel

(3)

(4)

其中：S表示相关值，下标X表示数据(D)或者导频(P)通道的参数；下标I，Q分别表示I，Q支路的相关值；R(·)为本地伪码与经过滤波之后的输入信号的互相关函数；ΔF=F0-FD为本地载波和输入信号的频率差；Δτ=τ0-τ为本地伪码和输入信号的时延差；Δφ为本地载波和输入信号的相位差；d为调制电文和次级码等引起的符号位，取值为{+1,-1}，并且假设相干积分时间NTs不超过一个电文(次级码)宽度;ηX,I和ηX,Q为噪声ηIF经过积分器处理之后产生的高斯噪声，它们相互独立，并且具有相等的方差。

(5)

在单个通道进行捕获时，对获得的上述相关值SX=SX,I+jSX,Q进行求包络处理。

(6)

然后对Senv进行捕获判决。因为只利用了一个通道的信号功率，所以会降低捕获的性能。因而提出了数据和导频通道联合捕获的算法，主要对数据和导频通道的非相干联合捕获进行研究。

1.2非相干联合捕获

如图2所示，传统非相干联合捕获算法是直接对数据和导频的相关值进行平方求包络计算后相加，即

(7)

其中：SD=SD,I+jSD,Q，SP=SP,I+jSP,Q。

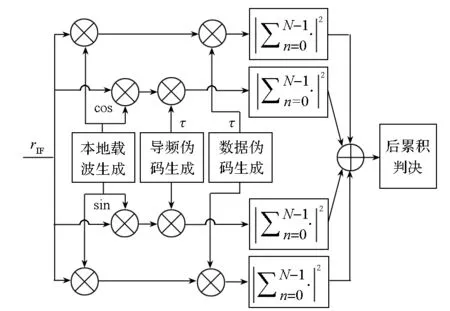
图2　非相干联合捕获相关值生成框图Fig.2　Non-coherent combining acquisition structure

当数据和导频通道功率相等时，此等权重的加权联合是合理的；但当二者的功率不相等时，数据和导频通道对捕获的影响应该是不同的。因此为了获得更好的捕获性能，可以采用加权系数进行联合捕获。

(8)

其中：α为数据通道的加权系数，取值范围为[0，1]，并且α的选择与功率分配有关。因而称此算法为功率加权联合捕获算法。

2性能分析

对于功率加权联合算法，其判决量的统计特性与传统捕获算法不相同。因此，本节将对功率加权联合捕获的性能进行分析。

2.1非相干联合捕获的虚警和检测概率

假设数据和导频通道的功率之和为C，即CD+CP，令功率分配系数μ=CD/C。根据捕获检测的原理，捕获包含H0和H1两种假设的判决。其中：H0表示信号不存在，或者本地多普勒频率、码相位估计不正确；H1表示在搜索的区间信号存在，并且本地多普勒频率、码相位估计均正确。

在H0假设条件下，相关值SD,I(FD,τ)，SD,Q(FD,τ)，SP,I(FD,τ)，SP,Q(FD,τ)均为零均值高斯白噪声，服从N(0,σ2)分布，其中方差σ2为N0fs/(4N)。

在H1假设条件下，码相位和多普勒频率估计值与真实值相差较小，即ΔF≈0，Δτ≈0。此时的相关值的分布特性如式(9)所示。

(9)

其中：φ为数据通道的载波相位差，并且数据通道和导频通道的相位差为π/2[2]。

(10)

其中ω为特征函数对应的频率值。

根据式(10)可以求出H0假设下的虚警概率。

(11)

(12)

(13)

其中Q2(a,b)为MarcumQ函数，具体表示为

(14)

其中I1(·)为一阶的第一类修正贝塞尔函数。

但是当α≠0.5时此表达式非常复杂，不利于计算。因此，根据文献[9]的方法利用快速傅里叶变换计算可以快速地获得SNC的检测概率。

2.2最优加权系数分析

通过以上分析可知，选择不同的加权系数会获得完全不同的虚警和检测概率，并且虚警和检测概率又与信号的强度以及功率分配比值μ相关。因此，难以通过理论推导获得最优的加权系数。采用数值分析方法对最优加权系数进行搜索，并通过数值拟合的方法获得最优加权系数与信号强度以及μ值的关系。

采用捕获等效检测因子的方法，对不同的检测和虚警概率的捕获性能进行比较。等效检测因子的定义[10]为:

D0=[erfc-1(2Pfa)-erfc-1(2Pd)]2

(15)

其中

(16)

根据式(10)和式(11)的结论，对μ为0.1，0.25，0.3以及0.4时的最优加权系数进行数值仿真分析。图3给出了μ=0.1时，不同加权系数和输入信号信噪比对等效检测因子的影响，可以看出加权系数影响着捕获的性能。

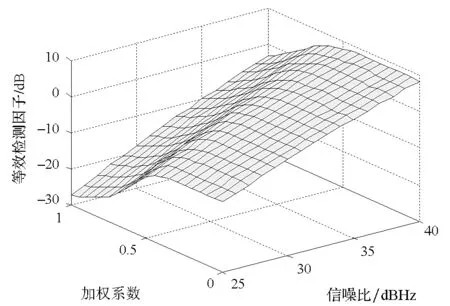
图3　μ=0.1时不同加权系数和信载噪比的捕获等效检测因子Fig.3　Equivalent detection factors with different weights and C/N0when μ=0.1

通过数值仿真分析，可以获得不同μ值和信噪比下的最优加权系数，如图4所示。考虑相干积分时间长度的影响，采用相关积分值的信噪比进行描述，其中SNR=C/N0×Tcoh，Tcoh为预检测积分时间。从图4可以看出，最优的加权系数与SNR的对数成近似二次方关系，可以采用最小二乘的方法对二者的关系进行拟合估计。

(17)

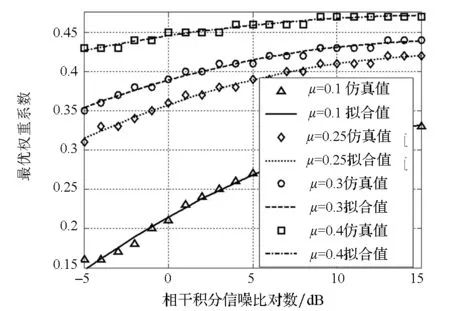
图4　不同相干积分信噪比下的最优加权系数Fig.4　Coherent integration SNR vs optimal weight coefficients

其中：SNRdB=10lg(SNR)，a，b，c为需要拟合的参数。采用最小二乘方法进行拟合得到的参数见表1。

表1　最优加权拟合系数

在完成捕获和跟踪之前，不能获得信号的信噪比，因此，不能对每一个载噪比的信号都获得最优捕获性能。但是，在设计捕获功能时，主要性能为捕获的灵敏度，也就是能够满足捕获条件的最低信噪比。因而，可以选择捕获门限信噪比对应的最优加权系数作为捕获模块的加权系数，这样既能够提高捕获的灵敏度，又能实现高于此信噪比门限的所有信号的捕获。

3仿真验证

通过仿真实验的方式进行捕获性能的验证，其中虚警概率和检测概率采用蒙特卡洛仿真结果的均值表示。对于所有的仿真，信号的生成参数见表2，表2中的信号带宽和码率等参数可以用于GPS L1C，北斗B1C信号的捕获。其中仿真过程忽略了前端滤波器带宽以及量化的非线性等影响。

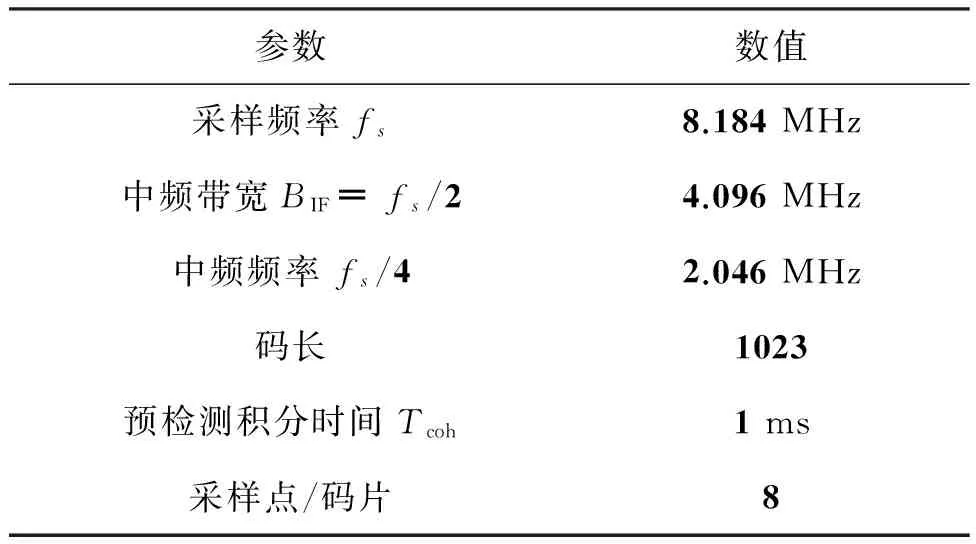
表2　捕获仿真参数

图5给出了当μ=0.25时，功率加权联合捕获接收工作特性(Receiver Operating Characteristics, ROC)曲线图。其中当α=0.5时，捕获的性能即为传统非加权联合的性能。从图5中可以看出在35 dBHz条件下，加权系数α=0.3的捕获性能优于传统捕获性能。图5同时给出了信号载噪比为40 dBHz时，不同加权系数的捕获ROC曲线。此时，α=0.3具有较好的捕获性能。

图5　μ=0.25时非相干联合捕获ROC曲线Fig.5　ROC curve of non-coherent combining acquisition when μ=0.25

图6给出了μ=0.25，虚警概率Pfa=10-3时，加权系数α为0.3和0.5时的检测概率曲线。从图6中可以看出，采用加权联合的性能相对于传统的捕获算法性能稍有提升，在检测概率Pd=0.8时提升了约0.4 dB的性能。

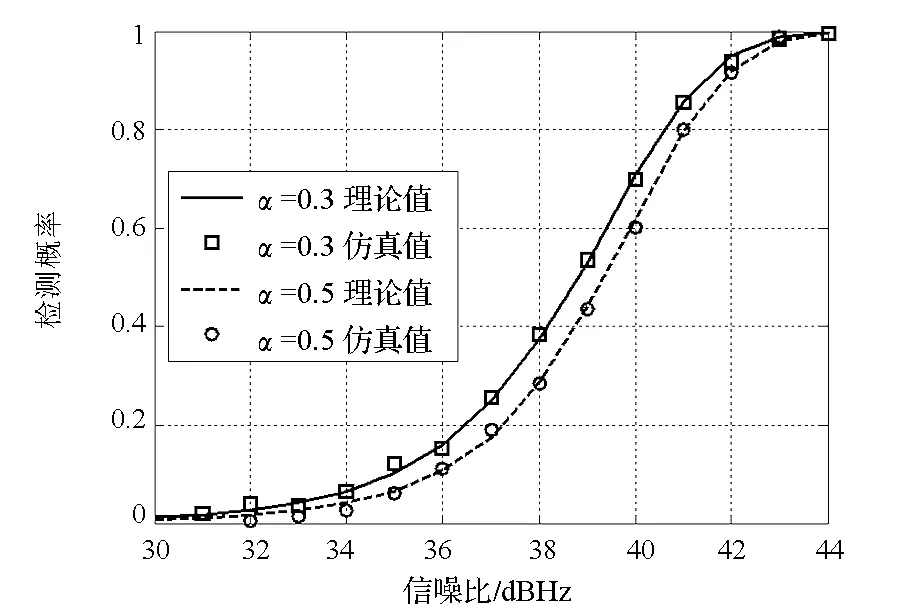
图6　μ=0.25，Pfa=10-3时检测概率与信噪比关系图 Fig.6　Detection probability vs C/N0when μ=0.25 and Pfa=10-3

4结论

对数据和导频通道功率不相等条件下的非相干联合捕获算法进行了分析，并针对此特点提出了加权联合捕获算法。推导了非相干加权联合捕获的虚警和检测概率求解方法，并通过仿真验证其正确性。通过数值分析的方法进行了最优加权系数与相干积分信噪比的二次方拟合，获得了不同功率分配比下的最优加权系数。

通过理论和仿真实验表明，当μ=0.25，Pd=0.8，Pfa=10-3时，最优加权联合捕获相对于传统捕获提升了0.4 dB的捕获性能。所以在进行GPS的L1C信号捕获时，因为其数据和导频通道的功率不相等，采用功率加权的联合捕获算法能够提高捕获的性能。

参考文献(References)

[1]Global Positioning Systems Directorate. Navstar GPS space segment/user segment L1C interface (IS-GPS-800D)[R]. Official US Government Information about the Global Positioning System (GPS) and Related Topics, 2013.

[2]Borio D, O′Driscoll C, Lachapelle G. Coherent, noncoherent, and differentially coherent combining techniques for acquisition of new composite GNSS signals[J]. IEEE Transactions on Aerospace and Electronic Systems,2009, 45(3): 1227-1240.

[3]Borio D, Mongredien C, Lachapelle G. New L5/E5a acquisition algorithms: analysis and comparison[C]//Proceedings of IEEE 10th International Symposium on Spread Spectrum Techniques and Applications,Bologna, Italy, IEEE, 2008: 53-57.

[4]Kewen S, Presti L L. Channels combining techniques for a novel two steps acquisition of new composite GNSS signals in presence of bit sign transitions[C]//Proceedings of IEEE/ION Position Location and Navigation Symposium (PLANS), Indian Wells, CA, USA, IEEE, 2010: 443-457.[5]Ta T H, Dovis F, Margaria D, et al. Comparative study on joint data/pilot strategies for high sensitivity galileo E1 open service signal acquisition[J]. IET Radar, Sonar & Navigation, 2010, 4(6): 764-779.

[6]Gernot C. Development of combined GPS L1/L2C acquisition and tracking methods for weak signals environments[D]. Canada:University of Calgary, 2009.

[7]Macchi-Gernot F, Petovello M G, Lachapelle G. Combined acquisition and tracking methods for GPS L1 C/A and L1C signals[J]. International Journal of Navigation and Observation, 2010, 2010: 1-19.

[8]Simon M K. Probability distributions involving Gaussian random variables: a handbook for engineers and scientists[M]. Holland:Kluwer Academic Publishers, 2007.

[9]Nuttall A H. Accurate efficient evaluation of cumulative or exceedance probability distributions directly from characteristic functions[R]. DTIC Document, 1983.

[10]Barton D K. Simple procedures for radar detection calculations[J]. IEEE Transactions on Aerospace and Electronic Systems, 1969, 5(5): 837-846.

doi:10.11887/j.cn.201602019

*收稿日期：2015-04-07

基金项目：国家自然科学基金资助项目(61403413)

作者简介：田丰(1986—)，男，湖南常德人，博士研究生，E-mail：amazetian@icloud.com；欧钢(通信作者)，男，教授，博士，博士生导师，E-mail：ougang@sina.com

中图分类号：TN96

文献标志码：A

文章编号：1001-2486(2016)02-112-05

Power-weighted combining acquisition algorithm with data and pilot signals

TIAN Feng, TANG Xiaomei, OU Gang

(School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract：The modulation with different power of data and pilot channels will be used in the next generation of global navigation satellite systems. However, the traditional acquisition algorithms are mostly designed with equal-weighted coefficient of data and pilot channels. When the power of data and pilot channels is not equal, the traditional algorithms are not suitable for optimizing the performance. A power-weighted combining acquisition algorithm, which uses the different weighted coefficients for data and pilot channels, was proposed. The Least-Square fitting method was used to optimize the coefficients. The detection and false-alarm probabilities were derived with characteristic function of decision variable. The simulations prove that the acquisition threshold of the algorithm is improved by 0.4 dB when the power ratio of data and pilot channels is 1 ∶3, and the detection and false-alarm probabilities are 0.8 and 10-3respectively.

Key words：incoherent; combining acquisition; pilot channel; weighted coefficient; characteristic function

http://journal.nudt.edu.cn