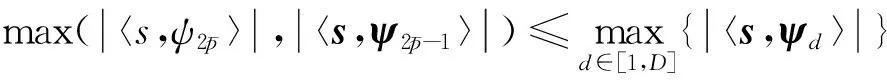运用改进正交匹配追踪算法精确估计跳频信号跳变时刻*
2016-07-26沙志超盛卫东
沙志超,盛卫东,徐 湛,李 骏
(国防科技大学 电子科学与工程学院, 湖南 长沙 410073)
运用改进正交匹配追踪算法精确估计跳频信号跳变时刻*
沙志超,盛卫东,徐湛,李骏
(国防科技大学 电子科学与工程学院, 湖南 长沙410073)
摘要:现有方法得到的跳变时刻精度不高、抗干扰能力较弱,为此提出一种运用改进正交匹配追踪算法的跳变时刻精确估计方法。根据跳频信号原理建立跳变时刻估计的稀疏表示模型,用改进正交匹配追踪算法求解该模型,获取跳变时刻。理论分析和仿真结果证明该方法能够获取高精度的跳变时刻,估计性能方面优于现有算法。
关键词:跳频信号;稀疏重构;时频分析;正交匹配追踪
跳频通信以其良好的抗干扰性、低截获概率及组网能力在军事战术通信中得到广泛应用[1]。跳频信号参数估计是跳频通信对抗的重要任务,而估计跳变时刻是全部跳频参数估计的关键[2-3]。
现有的跳变时刻估计方法主要包括时频分析方法[4-10]、原子分解方法[11]、自回归滑动平均(Auto-Regressive and Moving Average, ARMA)模型方法[12]、稀疏线性回归(Sparse Linear Regression, SLR)方法[2]等。时频分析方法包括短时傅里叶变换(Short Time Fourier Transform, STFT)、Gabor变换、Wigner-Ville分布、平滑伪Wigner-Ville分布(Smoothed Pseudo Wigner-Ville Distribution, SPWVD)及重排类时频分布方法[4]。时频分析方法[5-10]估计跳变时刻普遍存在精度不高,抗干扰能力弱的缺点。文献[11]提出了基于原子分解的跳频参数盲估计方法,该方法需要在庞大的时频原子字典中迭代搜索,计算量大,很难投入到应用中。文献[12]用ARMA模型描述含噪跳频信号,利用跳变点对模型的影响来跟踪跳频信号,该算法理论性较强,主要针对多通道接收的情况,实时性较强但信噪比适应能力极弱。文献[2]用SLR方法解决多个跳频信号同时存在时的跳频参数估计问题,利用跳频信号时频稀疏性,在高信噪比条件下取得较好的效果,但在低信噪条件下性能较差且计算量较大。
为了精确估计跳频信号的跳变时刻,沙志超等以现有时频分析方法的粗估结果为基础,提出了一种基于改进匹配追踪算法(Improved Orthogonal Matching Pursuit,IOMP)的跳频信号跳变时刻精确估计方法。该方法能够在低信噪比情况下精确估计跳变时刻。
1跳频信号及跳变时刻稀疏表示模型
1.1跳频信号模型
根据跳频信号的产生原理,假设在观测时间
T内有M个跳频信号进入接收机,则单天线接收的跳频信号为:
(1)
其中:sm(t)表示第m个跳频信号,v(t)表示零均值、方差为σ2的加性高斯白噪声。对于第m个跳频信号,设其跳周期为Tm,第k跳对应的载频为fmk,第0跳持续时间为αTm(0<α≤1),则sm(t)可以表示为:
(2)

1.2跳变时刻稀疏表示模型
常规的稀疏重构理论[13]考虑信号y∈P在一组标准正交集ψ1,ψ2,…,ψP上是稀疏的,则信号可以表示为:

(3)
其中:Ψ=[ψ1,ψ2,…,ψP]∈P×P,αi=〈y,ψi〉,α∈P且。针对频域稀疏信号,可以设计Ψ是由频率网格划分构成的傅里叶正交基,ψi=[ejωi1,ejωi2,…,ejωiP]T,频率ωi=2πi/P。
当y中发生频率跳变时,式(3)的α就不再具有稀疏性,常规的稀疏表示模型将不再适用。在跳变频率未知的情况下,建立文献[2]中的稀疏模型,矩阵Ψ的维数为P×P2,且求解过程的矩阵求逆导致计算量很大。考虑到现有的时频分析方法可以得到粗估的跳变时刻和较为准确的跳频频率,下面利用这些信息建立精确估计跳变时刻的稀疏表示模型。采用如下方法选取观测数据。以粗估跳变时刻为中心,在观测长度P内每个跳频信号最多包含一个跳变点。依据该数据截取方法,以观测数据段内是否包含跳变点为标准,每个跳频信号有两种可能:在位置p∈[2,P-1]处由频率ωi跳变到ωj,或在观测时间内频率恒定。对包含跳变点的跳频信号,依次改变频率跳变位置得到观测矩阵A=[a1,a2,…,aP-2]∈P×2(P-2),其中:
(4)
对于频率恒定的跳频信号观测矩阵由一个单频列向量和一个零向量组成,表示为:
(5)
每一个跳频信号根据频率变化情况设计一个对应矩阵,并将全部信号的矩阵依次按列扩展为一个综合的观测矩阵Ψ,以两个跳频信号为例,一个包含跳变点,另一个频率恒定,则观测矩阵Ψ=[A, Φ]。
2IOMP算法
2.1OMP算法原理
正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)[14]属于贪婪类算法,每次迭代过程中寻找Ψ中与观测向量相关性最大的列向量,并在观测向量中去掉所选列集合的影响。经过m次依次迭代,找出Ψ中组成观测向量的列向量集合。文献[15]中用理论和仿真证明了OMP算法能够在含噪情况下很好地恢复稀疏信号。OMP算法描述如下。
步骤1:输入观测数据y,观测矩阵Ψ,稀疏度k。
步骤2:初始化冗余信息r0=y,列向量位置的集合Φ0=Λm=∅,迭代次数t=0。
步骤3:进行算法迭代。
1)通过式(6),得到列向量位置λt。
(6)
2)扩展Φt=[Φt-1φλt],Λt=Λt-1∪{λt}。
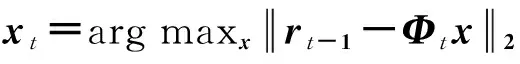
4)计算近似观测信号at=Φtxt和冗余信息rt=v-at。
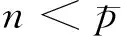
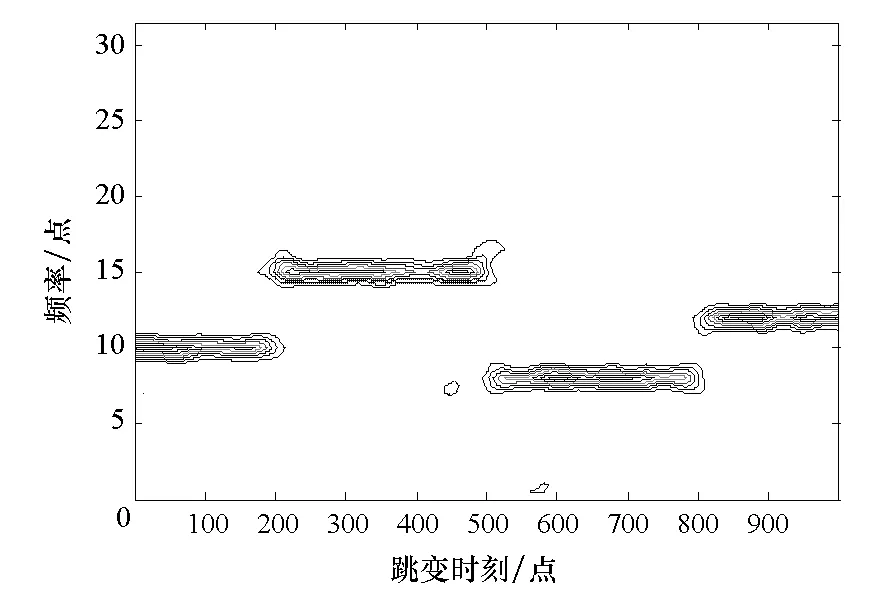
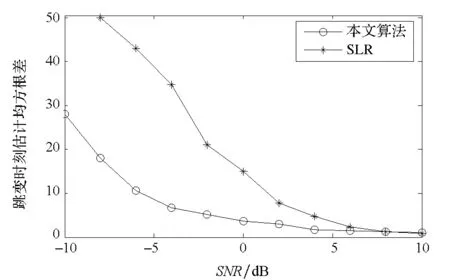
5)t=t+1,如果t 2.2IOMP算法原理 式(3)中稀疏表示矩阵ap的两列代表一个跳变时刻,两列的线性组合共同表示跳频信号。因为Ψ中与观测数据相关性较大的列不一定代表真实的跳变时刻,而真实跳变时刻对应矩阵ap的单列与观测数据的相关值很可能不是最大,所以式(6)的子空间选取方法不能适应两列组合选取的情况。为了求解2.1节的稀疏表示模型,对OMP算法的子空间选取规则做了修改。 考虑包含跳变点的信号 (7) 当d=2n-1时,则 (8) 当d=2n时,则 (9) (10) (11) 通过以上分析可知虽然真实跳变时刻对应的矩阵ap的单列相关值很可能不取最大,但在理论上与跳频信号跳变点匹配的矩阵ap两列相关值之和应该取最大值。因此,IOMP方法在子空间选取时要以两类相关值之和为选取标准。首先计算冗余信息与观测矩阵各列的相关值。 (12) 然后将λt(j)的第2n-1位与第2n位相加得到λ′t(n),取λ′t(n)的最大值位置作为与观测数据匹配的向量ap位置。 (13) 在集合Φt扩展时将根据式(13)选取的两列统一加入集合,其他过程与2.1节算法相同。 2.3性能分析 根据IOMP算法的原理,其计算量由式(12)中的向量相关计算决定。如果式(12)中向量的维数记为L,其计算量可表示为2L。如果数据中包含m个跳变时刻,则矩阵Ψ包含2mL列,完成m个跳变时刻估计需要运行式(12)的次数为2m2L。综上所述,IOMP算法完成m个跳变时刻估计的计算量约为(2mL)2,计算量与数据分段长度的平方成正比。因此为了控制计算量,在利用该算法时尽量把跳变时刻放在数据分段的中间,且分段长度不能太长。 由于IOMP算法在向量划分时以采样点为单位,因此IOMP算法估计跳变时刻的精度可以精确到采样点。而传统的时频分析方法存在时频不确定性,在保证频率估计精度前提下窗长度不能太短,这就影响了时间的估计精度。 3算法仿真 通过仿真试验验证提出算法估计跳变时刻的性能。仿真1以单跳频信号为分析对象,验证算法的有效性及信噪比适应能力。因为文献[12]中的ARMA模型方法主要针对阵列接收且要求信噪比较高,所以本文列为比较对象。选择典型的时频分析方法[8]、稀疏表示类的SLR方法[2]进行仿真比较。仿真2是以两个跳频信号为分析对象,分析多用户对算法信噪比适应能力的影响。 3.1单跳频信号时频分析仿真 频率集个数P=64,网格均匀划分,频率集W={2πp/P},p=0,2,…,P-1。观测数据采样点长度为1000,跳变周期为300点,第一跳的持续时长为200点,各跳变的频率依次为[ω10,ω15,ω8,ω12],信噪比为0 dB时SPWVD方法得到的时频图如图1所示。用本文算法估计的跳变时刻与真实值的比较如图2所示。由图2可知,本文算法可以准确估计该仿真跳频信号的跳变时刻。图3给出了信噪比从-10 dB到16 dB变化时,本文算法与文献[2]中SLR方法、文献[8]中SPWVD方法的跳变时刻估计精度的比较。每组仿真条件下,分别进行100次Monte-Carlo仿真。 图1 SPWVD方法时频分析结果(单信号)Fig.1 SPWVD distribution (one signal) 图2 SNR=0 dB时本文算法跳变时刻估计结果Fig.2 Estimation result of hop timing in SNR=0 dB 图3 算法性能比较(单信号)Fig.3 Performance comparison (one signal) 从图3可以看出,在信噪比低于0 dB时本文方法性能明显优于其他三种算法,在信噪比大于0 dB时本文方法与SLR方法性能相当,且估计偏差逐渐趋于0,SPWVD方法在高信噪比情况下仍存在的估计偏差。 3.2多跳频信号时频分析仿真 在仿真1的基础上在增加一个跳频信号,跳变周期为400点,第一条的持续时长为100点,各跳变的频率依次为[ω10,ω16,ω8,ω12,ω18,ω14]。信噪比为0 dB时SPWVD方法得到的时频图如图4所示,各时刻对应频谱最大值如图5所示。可以看出,传统的跳变时刻估计方法不能适应多用户情况。 图6为不同信噪比条件下本文算法与SLR方法估计跳变时刻的平均偏差的比较。从图6可以看出,本文算法信噪比适应能力明显优于SLR方法。 图4 SPWVD方法时频分析结果(两信号)Fig.4 SPWVD distribution (two signals) 图5 时频分布各时刻的频谱最大值Fig.5 Frequency spectrum maxima of time-frequency distribution 图6 算法性能比较(两信号)Fig.6 Performance comparison (two signals) 4结论 由于目前已有的跳频信号跳变时刻估计方法估计精度低,信噪比适应能力较差,于是提出一种基于IOMP算法的跳频信号跳变时刻精确估计方法。仿真试验结果表明本文方法具有高精度的跳变时刻估计能力,建立的稀疏重构模型能够适应多跳频信号情况,在估计精度、信噪比适应能力上均优于现有算法。另外,本文算法是属于贪婪类算法,具有计算量小的优点。但在分析时只考虑频率值完全匹配的情况,模型频率失配时的性能需要进一步研究。 参考文献(References) [1]Torrieri D J. Mobile frequency-hopping CDMA systems [J]. IEEE Transactions on Communication, 2000, 48(8): 1318-1327. [2]Daniele A, Georgios B G, Nicholas D S. Estimating multiple frequency-hopping signal parameters via sparse linear regression [J]. IEEE Transactions on Signal Processing, 2010, 58(10): 5044-5056. [3]Liu X, Li J, Ma X. An EM algorithm for blind hop timing estimation of multiple FH signals using an array system with bandwidth mismatch [J]. IEEE Transactions on Vehicular Technology, 2007, 56(5): 2545-2554. [4]张贤达, 保铮. 非平稳信号分析与处理[M]. 北京: 国防工业出版社, 1998: 20-70. ZHANG Xianda, BAO Zheng. Analysis and processing of nonstationary signals[M]. Beijing: National Defence Industry Press, 1998: 20-70.(in Chinese) [5]陈利虎, 张尔扬, 沈荣骏. 跳频信号的时频分析 [J]. 宇航学报, 2009, 30(2): 740-747. CHEN Lihu, ZHANG Eryang, SHEN Rongjun. Time-frequency analysis of frequency-hopping signals[J]. Journal of Astronautics, 2009, 30(2): 740-747. (in Chinese) [6]Barbarossa S, Scaglione A. Parameter estimation of spread spectrum frequency hopping signals using time-frequency distributions [C]//Proceedings of the First IEEE Signal Processing Workshop on Signal Processing Advances in Wireless Communications, 1997: 213-216. [7]赵俊, 张朝阳, 赖利峰, 等. 一种基于时频分析的跳频信号参数盲估计方法[J]. 电路与系统学报, 2003, 8(3): 46-50. ZHAO Jun, ZHANG Zhaoyang, LAI Lifeng,et al. Blind parameter estimation of frequency-hopping signals based on time-frequency analysis [J]. Journal of Circuits and Systems, 2003, 8(3): 46-50. (in Chinese) [8]Chen T C. Joint signal parameter estimation of frequency-hopping communications [J]. IET Communications, 2012, 6(4): 381-389. [9]张曦, 杜兴民, 朱礼亚. 基于重排SPWVD的跳频信号参数提取方法[J]. 计算机工程与应用, 2007, 43(15): 144-147. ZHANG Xi, DU Xingmin, ZHU Liya. Blind parameters extraction of frequency-hopping signals based on reassignment SPWVD [J].Computer Engineering and Applications, 2007, 43(15): 144-147. (in Chinese) [10]Lei Y K, Zhong Z F, Wu Y H. A new hop duration blind estimation algorithm for frequency-hopping signals [C]//Proceedings of 2008 IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application, 2008: 695-699. [11]Fan H N, Guo Y, Feng X. Blind parameter estimation of frequency hopping signals based on matching pursuit [C] //Proceedings of Wireless Comunication, Networking and Mobile Computing, 2008: 1-5. [12]Liu Z M, Huang Z T, Zhou Y Y. Hoppinginstants detection and frequency tracking of FH signals with single or multiple channels [J]. IET Communications, 2012, 6(1): 84-89. [13]Candas E J, Waldn M B. An introduction to compressive sampling [J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30. [14]Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666. [15]Cai T T, Wang L. Orthogonal matching pursuit for sparse signal recovery with noise [J]. IEEE Transactions on Information Theory, 2011, 57(7): 4680-4688. doi:10.11887/j.cn.201602018 *收稿日期:2015-03-13 基金项目:国家自然科学基金资助项目(61302141) 作者简介:沙志超(1985—),男,河北沧州人,讲师,博士,E-mail:shazhichao_163@163.com 中图分类号:TN911.7 文献标志码:A 文章编号:1001-2486(2016)02-107-05 Hop timing precise estimation for frequency-hopping signals based on improved orthogonal matching pursuit algorithm SHA Zhichao, SHENG Weidong, XU Zhan, LI Jun (College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China) Abstract:The hop timing estimates derived from existing methods are coarse and unreliable, therefore, a novel method for estimating hop timing for frequency-hopping signals precisely was proposed based on an improved orthogonal matching pursuit algorithm. The sparse representation model for hop timing estimation was established according to the principle of frequency-hopping signals. Then, the improved orthogonal matching pursuit algorithm was used to solute the model and get hop timing finally. The theoretical analysis and simulation results verified that the method is capable of obtaining precise hop timing, and is better than current methods. Key words:frequency-hopping signals; sparse reconstruction; time-frequency analysis; orthogonal matching pursuit http://journal.nudt.edu.cn