曲线桥梁漂浮抗震体系地震模拟振动台试验及有限元分析

闫　磊， 李青宁， 程麦理， 尹俊红， 孙建鹏

(西安建筑科技大学 土木工程学院，西安　710055)



曲线桥梁漂浮抗震体系地震模拟振动台试验及有限元分析

闫磊， 李青宁， 程麦理， 尹俊红， 孙建鹏

(西安建筑科技大学 土木工程学院，西安710055)

摘要：针对曲线桥梁地震中损毁严重、修复困难等问题，提出曲线桥梁漂浮抗震体系基本概念、结构组成及设计方法，并探讨其工作原理。将漂浮抗震体系概念、方法用于制作的1/20曲线桥梁模型进行地震模拟振动台试验及有限元分析。结果表明，该模型桥梁在地震发生后桥墩顶加速度峰值较墩底降低率最大为24.6%，梁体在桥墩上部成漂浮状态能减小桥墩受力；试验过程中模型未倒塌，表明该体系抗震性能良好，可用于高烈度抗震地区的曲线桥梁设计。

关键词：曲线桥梁；漂浮抗震体系；振动台试验；有限元分析；抗震性能

曲线桥梁形状曲折、受力复杂、弯扭耦合效应显著，在历次破坏性地震中有相当多的曲线桥梁损毁严重[1-3]，其中不乏墩底、墩顶、墩梁连接破坏等震害，导致桥梁在震后修复困难或者无法修复。目前，国内外学者[4-9]虽在合理采用减、隔震措施以改善结构的抗震性能方面已取得一定进展，但大多集中在构造复杂的减隔震装置，且针对曲线桥梁较少。为此，本文在提出基于支座变形耗能、整体滑移隔震、 梁体大位移滑动后与防落梁耗能减震设施碰撞为一体的曲线桥梁飘浮抗震体系基础上对用该体系设计的1/20的S形模型桥梁进行地震模拟振动台试验及有限元分析，探讨运用漂浮抗震体系曲线桥梁的抗震性能，以期为曲线桥梁抗震设计提供试验依据。

1曲线桥梁飘浮抗震体系

曲线桥梁飘浮抗震体系由具有耗能减震能力的滑动支座及防落梁耗能减震措施共同构成。以预先设定的支座或耗能减震措施破坏为代价，确保桥梁结构在地震中不产生毁灭性破坏，震后只需局部更换元件便可快速恢复桥梁运营能力。

曲线桥梁飘浮抗震体系在整个地震过程中分三个工作阶段：第一阶段，正常使用状态或小震作用下，桥墩、支座及梁体无相对滑动，三者共同协调运动，此时地震能量仅靠支座的剪切变形消耗；第二阶段，中震作用下，支座开始出现滑动，一方面主要依靠支座与墩梁间的摩擦力及支座本身剪切变形耗能，另一方面支座滑动起到有效的隔震作用；第三阶段，大震作用下,支座已达最大可滑动范围，墩梁相对位移达最大容许变位，梁体与防落梁耗能减震措施碰撞耗能。三阶段简图见图1。

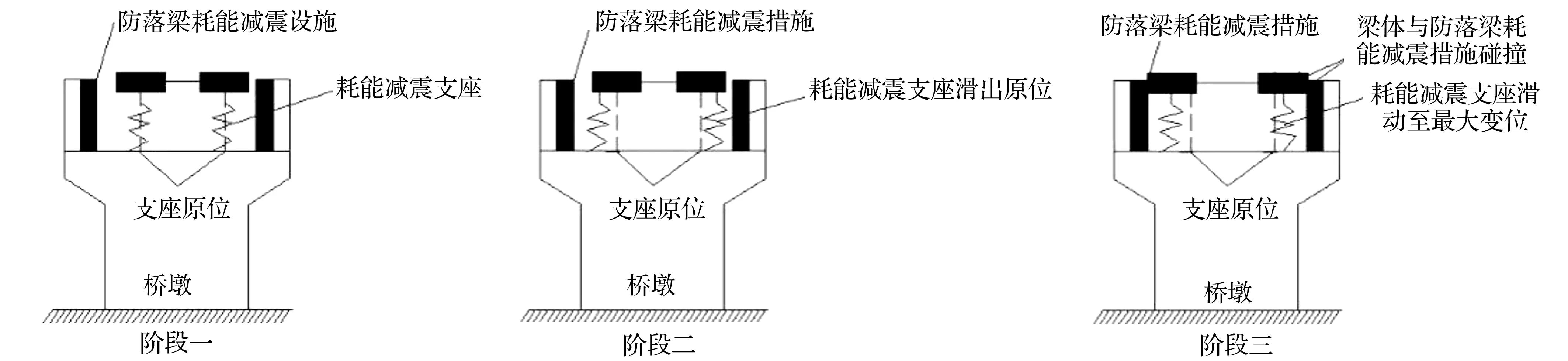
图1　漂浮抗震体系三阶段工作Fig.1 Three phases work of floating seismic system

2地震模拟振动台试验

2.1模型设计

以某S形曲线桥梁为研究背景，原型桥梁跨径组合为2 m×35.7 m，桥梁直线长度71.4 m，曲线长度77.3 m；S形曲线由圆曲线+缓和曲线+缓和曲线+圆曲线4部分组成，其中圆曲线段曲率半径均23 m，两段缓和曲线段曲率半径由23 m渐变至无穷大再渐变至23 m，各段长度为18.65 m+20 m+20 m+18.65 m。以原型桥梁为基础，制作相似比1/20的模型桥梁，模型的主要相似常数见表1，据表1设计的模型结构见图2。

表1　相似常数

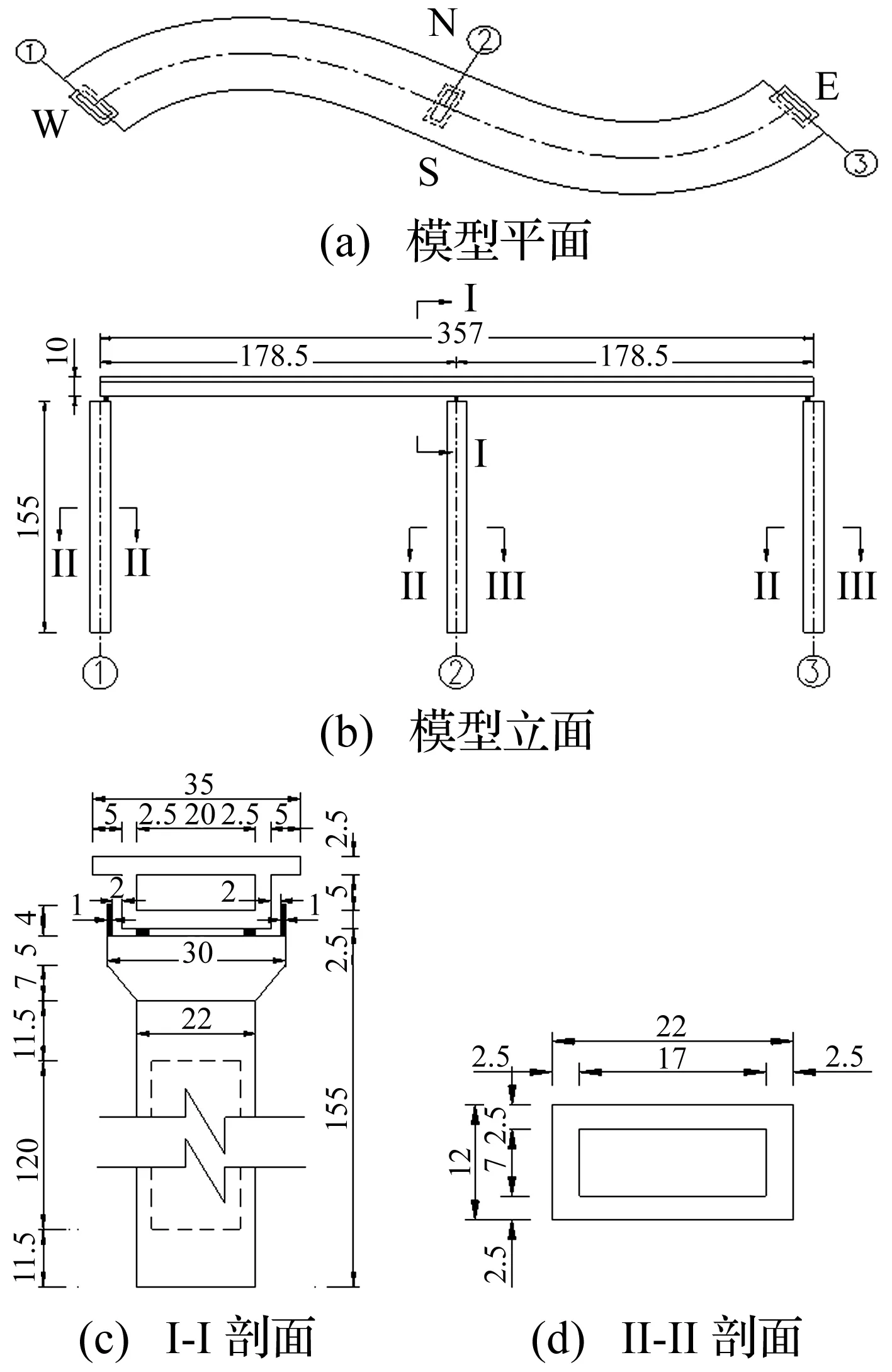
图2　模型设计(单位：cm)Fig.2Design of model(units:cm)

本文自行研制满足试验要求的微粒混凝土MC25模拟实际桥梁的普通混凝土C50，微粒混凝土可达相同混凝土强度，弹性模量较普通混凝土小，适宜缩尺比例振动台试验[9]。模型墩、梁纵筋用直径Φ6 mm的HRB335级带肋钢筋，箍筋用直径Φ6 mm HRB335级光圆钢筋；箍筋间距按6 cm设计，墩梁截面配筋见图3。模型空心部分填充泡沫板代替模板，墩、梁钢筋骨架见图4。模型桥每个桥墩上方均设置两个6 cm×6 cm×1.5 cm的普通橡胶支座，试验测得所用橡胶支座水平剪切刚度kx=ky=2.88×105N/m，竖向刚度kz=5.61 ×107N/m，支座与混凝土间摩擦系数为0.15。桥墩两侧设置4 cm高挡块，并粘贴1 cm厚挤塑板作为耗能减震材料，梁体与挤塑板初始间距设为2 cm(图2(c))。

据动力相似理论，模型试验须满足动力质量相似[10]，计算配重1 321.4 kg，实际配重1 040 kg，配重率达80%，满足振动台试验要求，配重模型见图5。

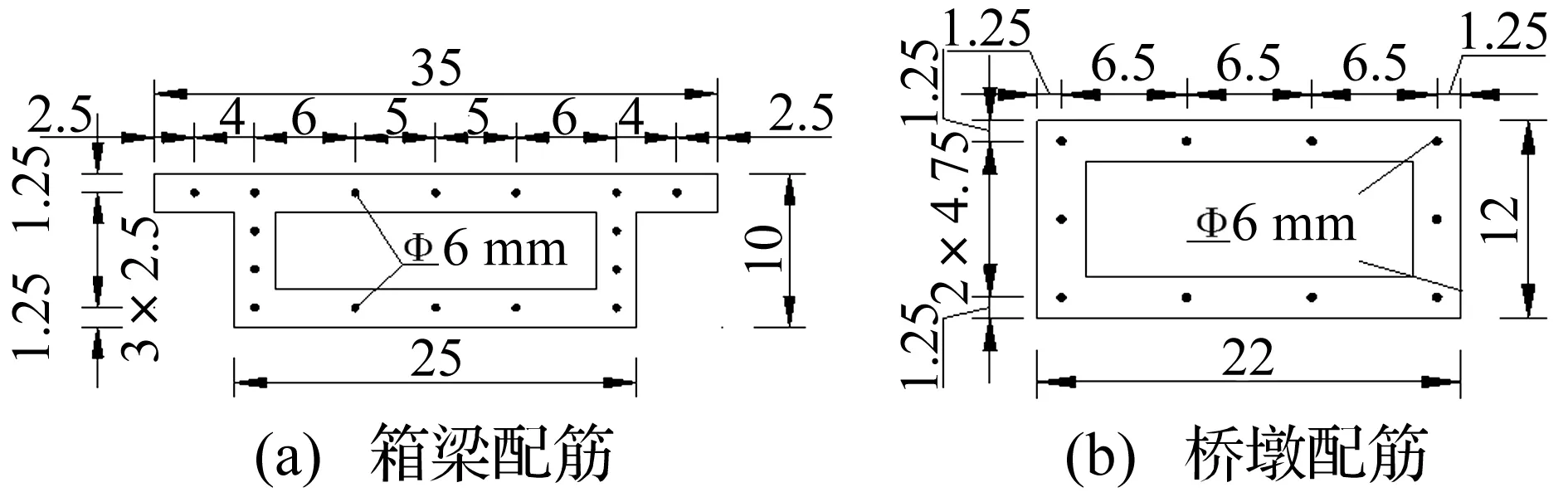
图3　截面配筋(单位：cm)Fig.3 Reinforcement assembly of section(units:cm)

图4　钢筋骨架Fig.4 Framework of steel reinforcement

图5　模型结构Fig.5 Model structure

2.2测点布置

据试验目的布设加速度、位移传感器，见图6、图7。

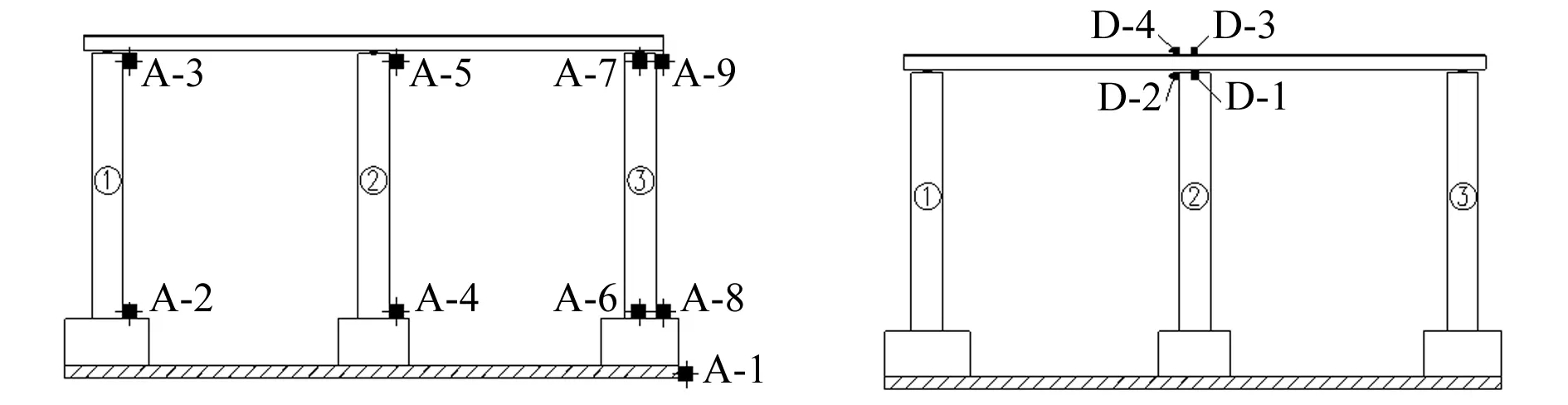
图6 加速度传感器布置Fig.6Layoutofaccelerometersensor图7 位移传感器布置Fig.7Layoutofdisplacementsensor

2.3地震波选取及输入方向

本试验主要反映桥梁在Ⅱ类场地土的动力反应，选El-Centro波(NS向)[11]为振动台输入地震波。模型结构底部用高强度螺栓与振动台面连接，模拟墩底固结边界条件，试验地震波沿1、3号桥墩连线方向输入。

表2　加载工况

2.4加载工况

振动台进行单个试件地震波加载为损伤累积过程，须严格按地震波幅值从小到大逐级加载[12-15]。因模型加速度相似系数为2.5，需将振动台输入加速度峰值调整为原设防烈度对应加速度峰值的2.5倍，本试验加载工况见表2。

3桥梁有限元模型

3.1支座单元模拟

本文用竖向受压为线弹性、水平向具有双向同性空间滑动支座单元[16]模拟板式橡胶支座，水平向恢复力模型见图8，其中k1、k2分别为支座发生滑动前、后刚度，计算模型中支座的水平剪切刚度、竖向刚度均严格按试验实测数据输入，kx=ky=k1=2.88×105N/m，竖向刚度kz=5.61×107N/m，当支座与墩顶、梁底接触面出现滑动后kx=ky=k2近似取0；Fcr为支座临界滑动摩擦力，由支座承受的竖向反力及摩擦因数共同决定。本文采用库伦摩擦假定，即摩擦因数在整个滑动过程中保持恒定，不受滑动速度及接触反力影响，板式橡胶支座接触面摩擦因数取0.15。

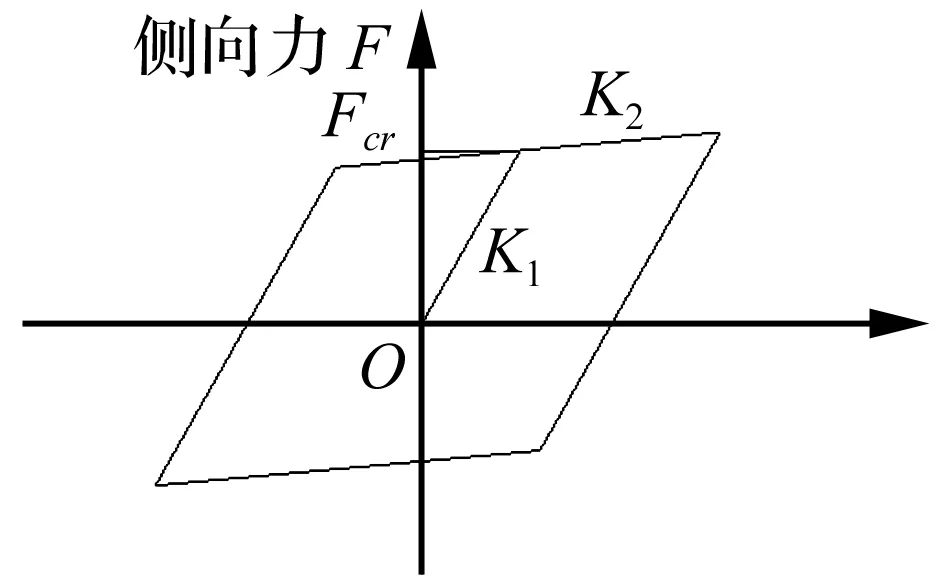
图8　板式橡胶支座恢复力模型 Fig.8 Lateral hysteresis for elastomeric pad bearing

3.2碰撞单元模拟

模型中横向碰撞单元用 Kelvin-Voigt (线性弹簧-阻尼模型)[17]，即由线性弹簧与阻尼器并联后与间隙单元串联而成。该模型中线性弹簧模拟碰撞力，阻尼器模拟碰撞中的能量耗损，间隙模拟梁体与挡块的初始间距。Kelvin-Voigt模型见图9，其中kk、ck、gp分别为碰撞刚度、黏滞阻尼系数及碰撞间隙。本文碰撞单元刚度kk取挡块抗弯刚度5.16×107N/m，ck=0.5，碰撞间隙gp=2 cm。

3.3其它假定

模型不考虑桩土相互作用，桥墩底部固结；桥墩用非线性弹塑性纤维梁柱单元模拟；上部结构用弹性梁单元模拟，建立计算模型见图10。

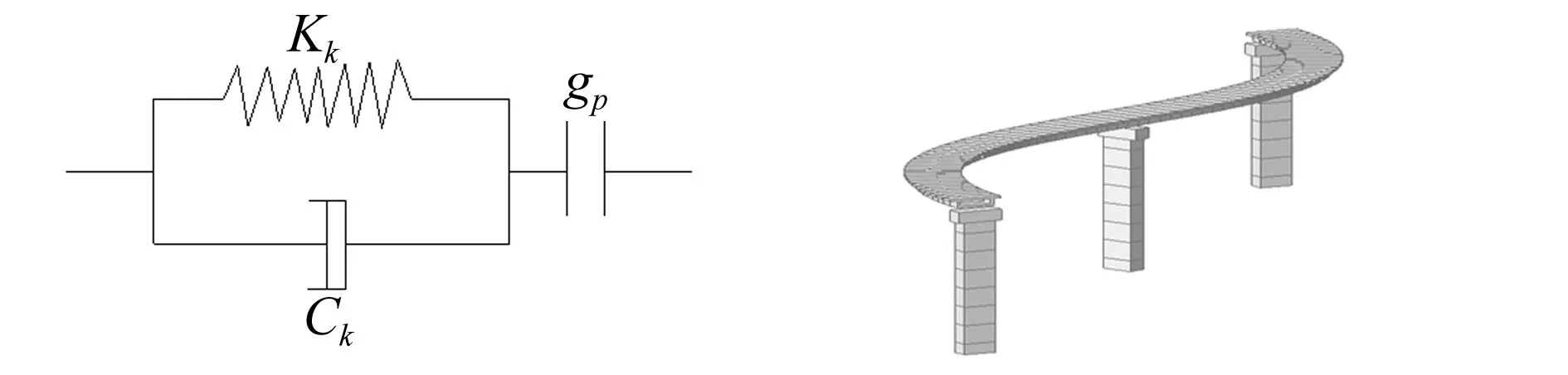
图9 碰撞单元模型Fig.9Poundingelementmodel图10 有限元模型Fig.10Finiteelementmodel

4试验及有限元分析

4.1试验现象

小震输入时桥梁结构基本无损伤；中震输入时桥墩底及墩中均有少量轻微水平、斜向裂缝出现，桥墩伴有轻微扭转发生；梁体产生轻微裂缝，随支座滑动梁体出现一定程度的平面内扭转；除1#、3#墩外弧侧支座均有2～6 mm径、切向滑动外其余各支座均未现明显滑动。大震输入时梁体与挡块碰撞，桥墩原有裂缝长、宽度均有不同程度扩展，并伴随新裂缝产生。总体讲，桥墩由于支座的滑移隔震作用使梁体因地震力引起的惯性力无法完全传递至桥墩，因而桥墩损伤较小，只需简要加固便可恢复使用性能；由于不同支座径向滑动位移存在差异较大，梁体发生明显的平面内扭转，随地震波幅值增加梁体平面内扭转程度亦增加，与挡块发生明显碰撞；大震时支座滑动非常严重， 3#墩外弧侧支座已基本脱离梁体。模型桥典型震害见图11。

图11　模型桥梁震害Fig.11 Damage of model bridge

4.2实测动力特性

本文对模型桥梁不同阶段基频进行测试计算，用结构动力学[18]中对数衰减率方法求出基频对应的阻尼比，用以反映模型桥梁刚度的退化特性。模型在不同工况加载的动力特性见图12。

由图12看出，模型结构自振频率从工况1～13依次为5.08 Hz、4.09 Hz、3.95 Hz、3.32 Hz、3.2 Hz、2.7

Hz、2.17 Hz，自振频率降低依次为19.6%、22.2%、34.7%、36.9%、46.8、58.3%，降低率较大。原因为：① 随地震波输入峰值增加，橡胶支座损伤较大，使桥梁结构边界条件发生改变，模型结构刚度下降，导致模型桥梁频率降低；② 模型在振动过程中梁体与墩身出现的裂缝等损伤导致刚度下降。

4.3加速度分析

工况2时测点A-2试验与有限元加速度时程曲线见图13，通过捡峰所得时程曲线峰值及用同样方法所得其它数据见表3。

由表3可知：工况2、4输入时支座尚无滑移，梁体基本与桥墩同步振动，桥梁结构处于弹性阶段，地震能量由支座剪切变形耗散，各桥墩基本表现为墩顶加速度峰值大于墩底。支座滑动后对桥梁起到有效隔震作用，使桥梁墩顶加速度峰值较墩底有所降低，本文对桥墩墩顶加速度峰值较墩底降低率进行计算。工况6加载时，2号墩实测加速度峰值降低率为17.7%；工况8加载时2号墩实测加速度峰值降低率为23.2%；3号墩底切向加速度峰值降低率为11.8%。工况10加载时2号墩顶加速度峰值降低率为15.4%；3号墩切向实测加速度峰值降低率为7.6%；3号墩径向实测加速度峰值降低率为24.6%。因此，随地震波输入峰值增大桥墩加速度峰值降低率明显增大；因地震波输入峰值增加致梁体在桥墩上方漂浮作用明显，梁体振动与桥墩振动不一致加强，故减震效果越明显。由于采用飘浮抗震体系，桥墩加速度峰值最大降低率达24.6%，表明该体系具有良好的抗震性能。

4.4位移分析

图12 模型结构频率、阻尼比变化Tab.12Changesoffrequencyanddampingratio图13 加速度时程曲线Fig.13Thetimehistorycurvedofacceleration图14 相对位移时程曲线Fig.14Relativedisplacementtimehistorycurve

由表4可知：随加速度峰值输入增加墩梁相对位移逐渐增大；工况2、4输入时墩梁相对位移较小，其主要源于支座的剪切变形。工况2、4、6、8输入时梁体因支座变形及滑动不一致产生平面内扭转，墩梁径向相对位移大于切向。工况10输入时梁体径、切向位移增大幅度明显，表明支座有滑动现象；由于梁体在径向与耗能减震挡块碰撞，径向相对位移小于切向。工况12输入时墩梁相对位移较工况10明显增加，表明梁体有明显飘浮。综上，地震波沿曲线桥梁桥墩连线方向输入时会引起其它方向振动，设计时应予考虑；通过支座变形耗能、梁体大位移后与耗能减震材料发生接触碰撞耗散地震能量；梁体在桥墩上部成飘浮状态减小地震作用下梁体惯性力向桥墩的传递，因而桥墩损伤较小。

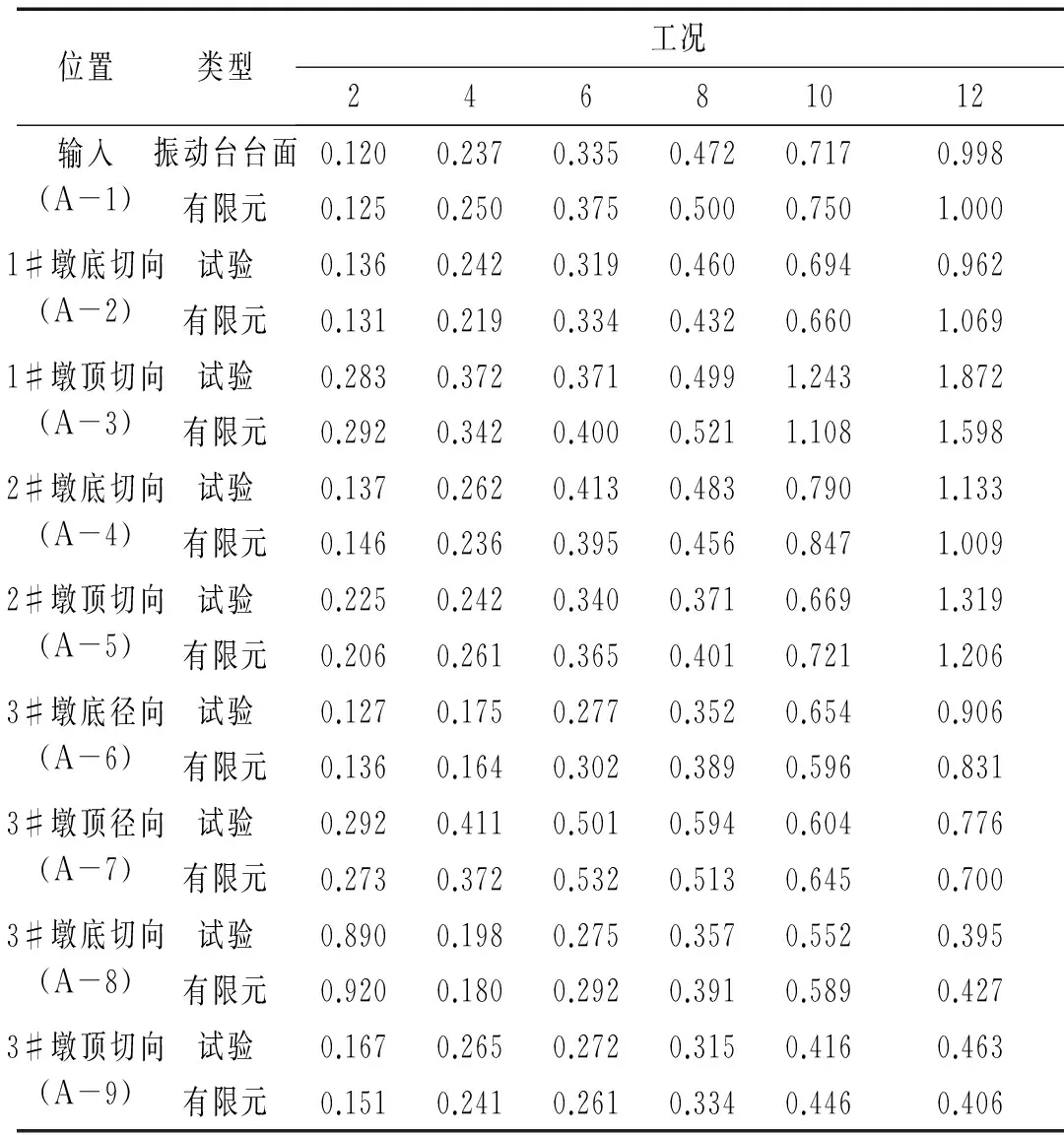
表3　各测点加速度峰值(g)

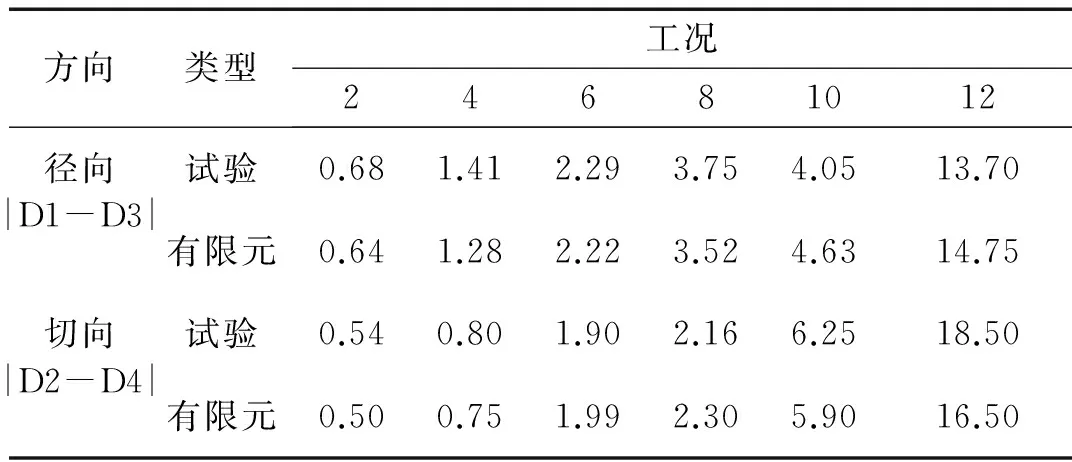
表4　墩梁相对位移峰值(mm)

4.5对比分析

据试验结果及有限元计算结果对动力特性、加速度及位移进行对比分析。

4.5.1动力特性对比

有限元分析计算模型结构一阶频率为4.51 Hz，与试验实测频率5.08 Hz相差11.2%。原因为：① 实际模型制作中因尺寸较小存在制作误差，导致实际模型与有限元模型存在一定差异；② 有限元模型配重均匀施加于模型，但实际试验因条件限制，配重施加过程中存在少部分不均匀现象；③测试过程中仪器精度及自振频率计算方法会引起一定误差。

4.5.2加速度对比

将不同工况的加速度有限元分析与试验测试结果进行对比，见图15。由图15看出，随地震波输入峰值增加，有限元与试验结果误差相应增加；工况2、4、6、8、10输入时有限元与试验结果较接近，误差在10%以内；工况12输入时2#墩顶切向加速度有限元与试验结果相差14.64%。此除动力特性对比中所列外亦有两点，即① 有限元建模为理想化无损伤模拟，实际模型在地震波加载过程中却为损伤累计的；② 由表3知试验中地震波并非完全按加载标准准确输入到模型桥梁，而有限元模型则准确将地震波施加于模型。总之，有限元结果与试验结果基本一致，表明有限元与试验结果的相互印证，也证明该体系引起的桥墩顶加速度峰值相对墩底降低，耗能效果显著。

4.5.3位移对比分析

将不同工况下墩梁相对位移有限元分析结果与试验测试结果对比，见图16。由图16看出，随地震波输入峰值增加两者间误差逐渐增大；工况2、4、6、8输入时有限元结果与试验结果误差基本在10%以内；工况10输入时墩梁径向相对位移有限元结果与试验结果相差14.41%；工况12输入时墩梁切向相对位移有限元结果与试验结果相差10.82%。引起此差别的主要原因除加速度对比中所列外尚有试验中大震输入时梁体在平面内有较大扭转，使梁径、切向位移计与墩顶径、切向位移计有一不可测的微小夹角，但有限元分析中无法模拟此差别，故大震作用时误差较大。有限元分析结果与试验结果均表明梁体因飘浮能减小桥墩在地震中受力。

图15 加速度峰值试验与有限元结果Fig.15Testandfiniteelementresultsofaccelerationpeak

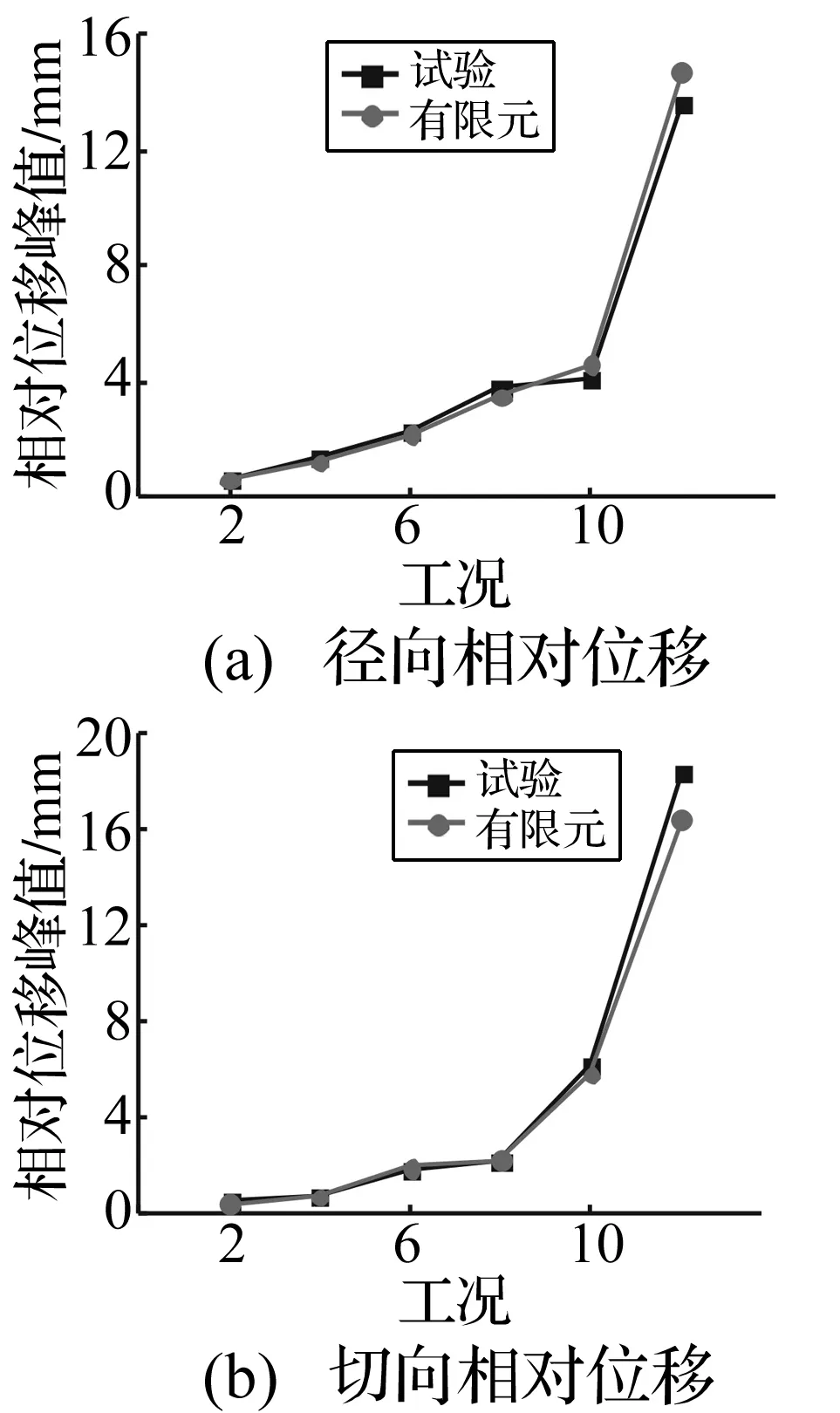
图16　相对位移峰值试验与有限元结果Fig.16 Test and finite element results of relative displacement peak

5结论

通过将漂浮抗震体系用于曲线桥梁的减隔震设计，并对采用漂浮抗震体系S形曲线桥梁进行地震模拟振动台试验及有限元分析，结论如下：

(1) 曲线桥梁漂浮抗震体系结构合理、工作机理明确、抗震效果显著，用于曲线桥梁的抗震设计完全可行。

(2) 应用漂浮抗震体系的模型桥梁，地震发生后桥墩顶加速度峰值较墩底降低率最大达24.6%，梁体在桥墩上部成漂浮状态能减小桥墩受力及损伤程度。

(3) 应用漂浮抗震体系的曲线桥梁，地震中虽支座、耗能减震挡块损伤严重，但较其它桥梁的震后修复，仅需更换支座或耗能减震挡块便可快速恢复桥梁的运营能力，从而提高震后救灾速度。

(4) 应用漂浮抗震体系的模型桥梁，正常使用状态或小震作用下支座剪切变形可消耗地震能量；中震后支座变形与滑移隔震作用共同工作能减小桥梁损伤；大震后支座变形耗能、滑移隔震、 防落梁耗能与减震措施协同工作，避免桥梁倒塌。

参 考 文 献

[1] 范立础. 桥梁抗震[M]. 上海:同济大学出版社，2001.

[2] 蔡中民, 武军. 桥梁工程抗震设计[M]. 北京：机械工业出版社,2008.

[3] 杜修力,韩强,李忠献,等．5·12 汶川地震中山区公路桥梁震害及启示[J]. 北京工业大学学报，2008, 34(12):1270-1279．

DU Xiu-li, HAN Qiang, LI Zhong-xian, et al. 5·12 Wenchuan earthquake damage and enlightenment in highway bridges[J]. Journal of Beijing University of Technology, 2008, 34(12): 1270-1279．

[4] 范立础,王志强．我国桥梁隔震技术的应用[J]. 振动工程学报,1999, 12( 2):173-181．

FAN Li-chu, WANG Zhi-qiang. Application of bridge seismic isolation technology in China[J]. Journal of Vibration Engineering, 1999, 12(2): 173-181．

[5] 汤虎,李建中. 地震动特性对公路桥梁板式橡胶支座滑动反应影响[J]. 工程力学, 2013, 30(10): 154-161.

TANG Hu, LI Jian-zhong. Effect of ground motion characteristics on sliding response of elastomeric pad bearings in highway bridges[J]. Engineering Mechanics, 2013, 30(10): 154-161.

[6] Dall’astaa A, Ragnib L. Nonlinear behavior of dynamic systems with high damping rubber devices[J]. Engineering Structures, 2008, 30(12): 3610-3618．

[7] Xing Chen-xi，Wang Hao，Li Ai-qun.Design and experi-mental verification of a new multi-functional bridge seismic isolation bearings[J]. Journal of Zhejiang University Science A,2012, 13(12): 904-914．

[8] Soneji B B, Jangid R S. Passive hybrid systems for earthquake protection of cable-stayed bridge[J]．Engineering Structures, 2007, 29(1): 57-70．

[9] 刘阳,刘文光,何文福,等.复杂博物馆隔震结构地震模拟振动台试验研究[J].振动与冲击,2014,33(4):107-112.

LIU Yang,LIU Wen-guang,HE Wen-fu,et al.Shaking table tests for a complex museum’s isolated structure[J].Journal of Vibration and Shock,2014,33(4):107-112.

[10] 沈朝勇,周福霖,黄襄云,等. 动力试验模型用微粒混凝土的初步试验研究[J]. 广州大学学报,2005(3):249-253.

SHEN Chao-yong, ZHOU Fu-lin, HUANG Xiang-yun,et al. Experimental research on mircroconcrete used in dynamic test model[J]. Journal of Guangzhou University,2005(3): 249-253.

[11] 周颖,吕西林. 建筑结构振动台模型试验方法与技术[M]. 北京：科学出版社,2012.

[12] CJJ166-2011,城市桥梁抗震设计规范[S].

[13] Jayaram N, Lin T, Baker J W. A computationally efficient ground-motion selection algorithm for matching a target response spectrum mean and variance[J]. Earthquake Spectra, 2011, 27(3):797-815.

[14] Baker J W. Conditional mean spectrum: tool for ground-motion selection[J]. Journal of Structural Engineering, 2010, 137(3):322-331.

[15] Baker J W, Jayaram N. Correlation of spectral acceleration values from NGA ground motion models[J]. Earthquake Spectra, 2008, 24(1):299-317.

[16] Jangid R S. Seismic response of sliding structures to bidirectional earthquake excitation[J]. Earthquake Engineering and Structural Dynamicas, 1996, 25: 1301-1305.

[17] 范立础,聂利英,李建中. 地震作用下板式橡胶支座滑动的动力性能分析[J]. 中国公路学报,2003, 16(4): 30-35.

FAN Li-chu, NIE Li-ying, LI Jian-zhong. Dynamic characteristic analysis of laminated rubber bearing sliding under earthquake[J]. China Journal of Highway and Transport, 2003, 16(4): 30-35.

[18] Anagnostopoulos S A. Equivalent viscous damping for modeling inelastic impacts in earthquake pounding problems [J]. Earthquake Engineering and Structural Dynamics, 2004, 33(8): 897-902.

[19] 王光远.结构动力学[M]. 北京:高等教育出版社,2006.

基金项目：国家自然科学基金(51078306)；国家自然科学基金青年基金(51408453)；高等学校博士学科点专项科研基金资助项目(20106120110004)；高等学校博士学科点专项科研基金资助项目(20136120120022)；陕西省自然科学基础研究计划资助项目(2013JQ7007)

收稿日期：2014-11-06修改稿收到日期：2015-01-30

通信作者李青宁 男，教授，博士生导师，1952年生

中图分类号:U442.55

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.001

Shaking table test and finite element analysis on curved bridge with floating seismic system

YAN lei, LI Qing-ning, CHENG Mai-li, YIN Jun-hong, SUN Jian-peng

(Civil Engineering School, Xi’an University of Architecture and Technology, Xi’an 710055, China)

Abstract:In view of that a curved bridge may be damaged severely in earthquake and its repair is as usual of much difficulty after earthquake, a floating seismic system for curved bridge was proposed, the basic concept, composition and design method of the floating systerm were presented and its working principle was discussed. A 1:20 scale curved bridge model with floating seismic system was built and the shaking table test and finite element analysis on it were conducted. The results show that after installing the floating seismic system, the maximum reduction rate of peak acceleration form the top to the bottom of the pier reaches 24.6 percent. Due to that the beam is floating above the pier, the dynamic force on the pier is reduced, so the bridge model does not collaspe in the test. It indicates that the seismic performance of the floating seismic system is good and it can be used for designing curved bridges built in high seismic intensity areas．

Key words:curved bridge; floating seismic system; shaking table test; finite element; seismic performance

第一作者 闫磊 男，博士生，1988年生