薄壁结构件铣削加工振动稳定性分析

蒋宇平， 龙新华， 孟　光

(上海交通大学 机械与动力工程学院振动、冲击、噪声研究所，上海　200240)



薄壁结构件铣削加工振动稳定性分析

蒋宇平， 龙新华， 孟光

(上海交通大学 机械与动力工程学院振动、冲击、噪声研究所，上海200240)

摘要：针对如何考虑刀具与工件相互耦合作用及加工位置对系统稳定性影响，通过对切屑厚度、铣削力建模，建立薄壁件铣削系统动力学模型，考虑薄壁件铣削稳定性受铣削位置影响，获得以轴向铣削深度、转速、铣削加工位置为参数的三维稳定性图。通过对曲面图分析，可确定在不同主轴转速、不同铣削区域内薄壁件各模态对铣削稳定性影响。通过时域模拟分析加工位置对系统失稳机制影响，揭示稳定铣削与不稳定铣削、不同模态在不稳定铣削时铣削力、铣削位移的变化规律。

关键词：铣削；稳定性；时变刚度；薄壁件

整体薄壁结构件具有重量轻、强度高、动力性能好等优点广泛用于航空、电子、模具等工业领域。而因其壁薄、刚度低，加工中易发生颤振。如何在提高加工效率的同时控制刀具、工件的相对振动，避免颤振一直为研究热点。对普通铣削加工，Tobias等[1-2]提出基于2D稳定性图的切削颤振避免方法。Sridhar等[3]用周期系数时滞微分方程组描述铣削过程动力学行为，并用扩展Floquet理论对方程组进行数值求解，确定稳定性图。Insperger等[4]提出基于Floquet理论的半离散铣削系统稳定性分析方法。丁烨[5]利用全离散法分析铣削稳定性及动态加工误差，并用二阶全离散法提高收敛性。对薄壁件，复杂薄壁类零件刚性差，数控加工时因铣削力等因素易变形，加工精度难以控制；而加工位置及材料去除对加工系统动态特性影响不可忽视。加工中引起薄壁件本身动态特性改变为评估稳定性难点，即铣削中工件刚度较低区域会极大影响铣削特性，铣削稳定性不在于简单决定主轴转速、临界铣削深度，而与铣削区域、工件各模态密切相关。Adetoro[6]用频率法分析薄壁铣削稳定性，并用表面加工质量实验进行对比。Bravo等[7-9]假设每一加工过程动态特性恒定，不同加工过程动态特性各不同，并据此研究薄壁件的铣削稳定性,建立薄壁件三维稳定lobe图。Tang等[10]用频率法建立关于转速及径向、轴向切深的三维稳定图。

本文以薄壁梁铣削精加工为例，忽略材料去除影响、考虑薄壁结构件不同位置刚度变化，建立具有多模态、变动态特性的铣削加工系统动力学模型，分析薄壁结构件铣削加工稳定性及失稳机制。

1薄壁梁铣削模型建立

1.1薄壁铣削模型

为研究薄壁件的铣削加工振动问题，以图1薄壁梁为研究对象，梁长0.3 m，宽0.04 m，厚0.01 m。弹性模量70×109Pa，密度2 700 kg/m3。因梁的纵向振动固有频率远大于横向振动前几阶，振幅远小于横向，故可忽略不计，薄壁梁横向振动微分方程为

(1)

式中：Fy(x,t)为工件位置x处、t时刻横向切削力；E为弹性模量；I为惯性矩；ρ为密度；A为固支梁横截面积。

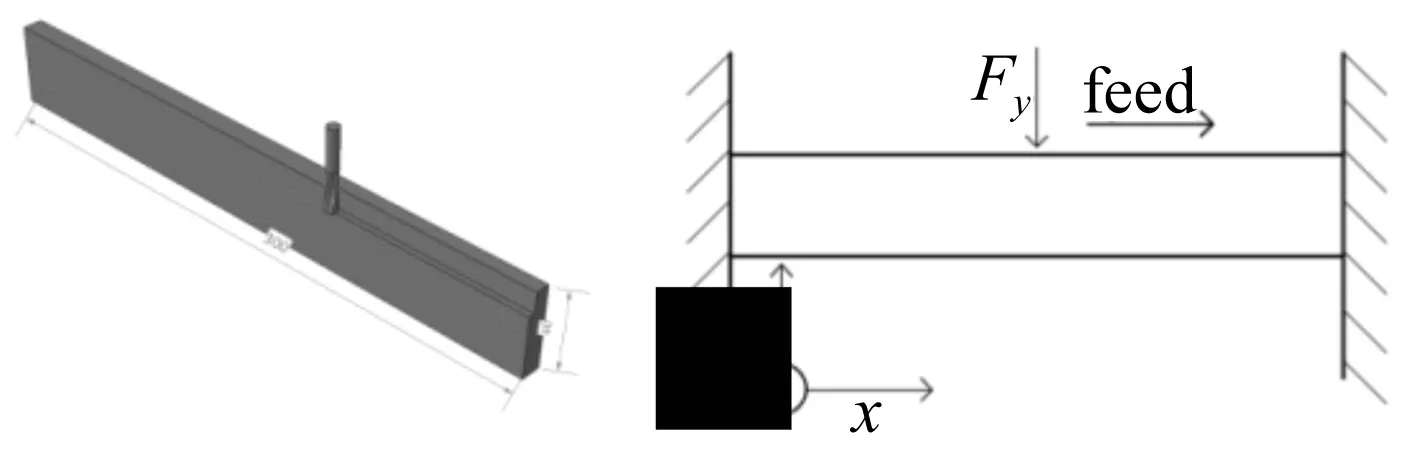
图1　薄壁件铣削示意图Fig.1 The structural sketch for thin-walled milling

1.2动态切削力

据斜角切削模型建立简化的切削力公式，切削力与切屑厚度成正比例关系，得

(2)

式中：kt为切向切削力系数；Kn为法向切削力系数与径向切削力系数之比；η为螺旋角；φn刀齿背面角；μ为切屑与刀齿摩擦系数；Fn为切削刃法向剖面径向力；Fc为切削刃法向剖面切向力；Fμ为垂直于平面摩擦力。

考虑薄壁件的弱刚性，刀具设为刚体,且只考虑y向振动，瞬时切屑厚度h为

h=flτsinθ(t,i,z)+

[y(t)-y(t-lτ)]cosθ(t,i,z)

(3)

式中：f为每齿进给量；τ为切削周期；l为考虑多重再生效应的时滞系数；θ为刀齿方位角。

为确定作用于薄壁件的动态切削力F(x,t)(图2)，将螺旋圆柱立铣刀沿z轴离散成长度为Δz的微元段，每个微元段受力见图2(b)。

图2　微元铣削力Fig.2 Micro-unit milling force

第i个齿在切向、径向及轴向的动态切削力为ΔFti，ΔFri，ΔFzi，即

(4)

据微元刀具坐标与全局坐标关系，作用于微元沿y向的力为

(5)

整理式(4)、(5)得

(6)

(7)

将式(3)代入式(6)，整理得

(8)

(9)

将式(9)沿轴向积分，得单个刀齿y向的力为

(10)

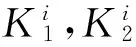
对所有刀齿切削力求和可得作用于刀具沿y方向的力Fy(t)，即

(11)

式中：K1，K2为刀具动态切削刚度系数。

展开上式，瞬时铣削力为

Fy(t)=K2y(t)-K2y(t-lτ)+K1lfτ

(12)

1.3模态参数

利用模态分解法，梁的横向振动可写为

(13)

式中：Wr(x)为第r阶固有振型函数，即

Wr(x)=Cr[sinh(βrx)-sin(βrx)+

αr(cosh(βrx)-cos(βrx)]

(14)

(15)

(16)

而Fy(x,t)=δ(x-vt)Fy(t)，设在t时刻铣削位置为x=xt，Fy(x,t)=δ(x-xt)Fy(t)，将式(15)、(16)代入式(1)，利用振型函数正交性，得

(17)

式中：L为工件长度。

对两端固支梁，用标准化阵型函数表达式，即Cr=1；则任意阶模态质量为

(18)

任意阶模态力为

(19)

将式(18)、(19)代入式(17)，简化为

(20)

进行拉普拉斯变换，即

(21)

式中：Qr(ω)为广义位移幅值；Fr(ω)为广义力幅值。

(22)

引入比例阻尼系数ζ，其频响函数为

由此获得切削点x1处第r阶等效质量mer、等效刚度ker及等效阻尼cer为

(23)

1.4铣削动力学方程

薄壁件在低转速下由于刚度较低及时变的动态特性，极易发生颤振；而高速铣削加工时高阶模态激励影响会使振动更复杂。考虑工件横向振动前两阶模态，振动位移为y(xt,t)=W1(xt)q1(t)+W2(xt)q2(t)。其中{W1，W2}为对应第一、二阶模态阵型；q=[q1q2]为工件第一、二阶模态坐标向量。系统振动方程为

(24)

式中：F1，F2为等效模态参数的广义力。

将铣削力表达式(12)代入上式，整理获得薄壁件前两阶模态的动力学方程为

(25)

式中：

以上铣削动力学方程属于变刚度的时滞微分方程，无解析解，只能通过数值方法进行时域仿真。在一个迭代步长内，延迟项由于已在上一周期内求得，因此式(25)右端项可视为常数项。将变时滞微分方程在每个迭代步长内转化为普通的常微分方程，并通过龙格库塔格式求解。

薄壁铣削中工件刚度始终在变化，故时域仿真中需不断更新等效模态参数，以获得刀具、工件接触点的振动位移及铣削力。随接触点移动，近固支点处，工件因中间刚度较小，振动位移逐渐增大。

2时域模拟

由于薄壁铣削过程中工件刚度较低，刀具相对工件可视作刚体。刀具几何、铣削力参数见表1。铣削加工、工件模态参数见表2、3。薄壁件横向振动等效刚度变化范围较大，不考虑材料去除即认为固有频率不变情况下固支梁两端不存在弹性变形，刚度无穷大，中间刚度较小，极易发生颤振。表3的模态参数表示在0.01～0.29 m之间等效刚度、质量变化范围。

表1　刀具参数

表2　铣削加工参数

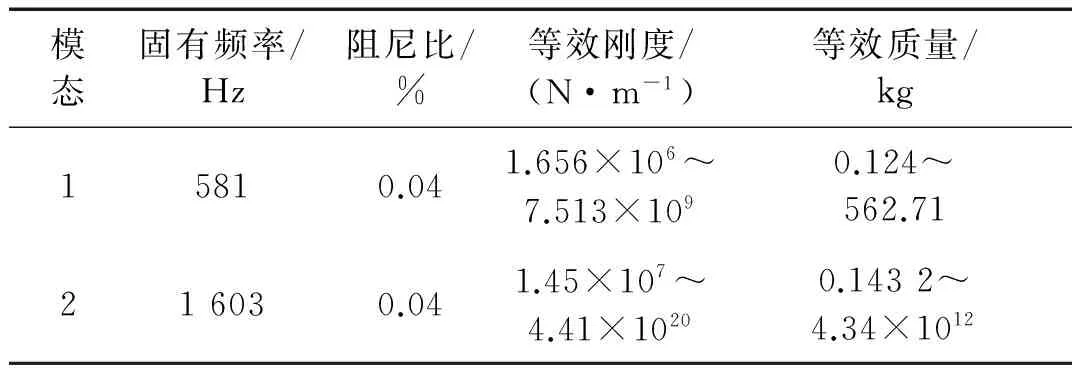
表3　模态参数

在6 000 r/min下稳态、非稳态薄壁梁铣削时域模拟见图3。图3(a)中深色为工况1，即轴向铣削深度(adoc)为0.1 mm时工件横向振动；浅色为工况2，即轴向铣削深度为0.22 mm时工件横向振动。两种工况下振动位移均远低于0.1 mm。图3(c)、(d)为工况2时铣削力及频谱分析。此时铣削力作为周期力激励， 呈

锯齿状。频谱主要为齿频(TPF)及倍频成分，因而轴向切深0.22 mm处为稳定切削。轴向切深继续增大至0.25 mm时(图3(b))，工件的横向振幅在中间较快达到0.1～0.15 mm。图3(e)、(f)为轴向切深0.25 mm的时域模拟频谱分析。当进给达到0.137 2 m时开始呈非周期运动的不稳定状态，但在0.168 2 m时不稳定状态开始消失，且消失位置与出现位置并未关于中间点对称，不稳定状态出现稍有延迟。图3(f)中不稳定状态已开始激发出多种颤振频率成分，先出现在工件第一阶固有频率附近的颤振频率(fcw)即由工件第一阶固频激发。当轴向切深缓慢增大至0.26 mm时，工件中间区域振幅急剧增大，而不稳定状态区域从中间向其它位置缓慢扩散。受限较低刚度，中间会严重降低整个薄壁件铣削加工的稳定极限切深。

3稳定性分析

为确定铣削系统稳定性，利用Floquet理论通过单个切削周期的状态转移矩阵特征值判断，即所有特征值的模小于1时系统稳定。对时滞系统因其具有无穷维即无穷多个特征值，故实际分析中多采用离散法，将无穷维系统离散成有限维系统，考虑利用有限维系统近似无限维系统所致误差，本研究采用数值积分进行时域分析，利用庞加莱截面判断系统时域的稳定性。对稳定的周期运动，庞加莱截面在相图上表示为有限个点；对失稳的准周期运动或其它运动形式，庞加莱截面在相图上由密集点形成一条闭合曲线或不规则分布点。

选表2中编号为2、3的加工参数，工件中间点等效刚度、质量作为模态参数进行时域模拟。轴向切深为0.22 mm、0.25 mm的时域模拟见图4，可见工件在adoc=0.22 mm时处于稳定状态，为0.25 mm时处于不稳定状态。其相图见图5，其中y(t)，v(t)分别为t时刻位移及速度，y(t-τ)为上周期振动位移。截取平面y(t-τ)=0，则庞加莱截面见图6。轴向切深为0.22 mm时，庞加莱截面收敛于一点，系统处于稳定状态；轴向切深增大至0.25 mm时呈不规则闭合曲线，系统处于不稳定状态。

图4 时域模拟Fig.4Timedomainsimulation图5 相图Fig.5Phasemap

图6　庞加莱截面Fig.6 Poincare section

铣削加工基于时域仿真的稳定性可由周期取样后相图判断。系统相图中最大位移、速度分别为S1、V1，最小位移为S2、V2；庞加莱截面的点通过齿周期采样获得，该截面最大位移、速度分别为s1、v1，最小位移、速度为s2、v2，则时域模拟的稳定性条件为

(27)

式中：α，β为比例常数，据要求取较小值。

当式(27)两条件同时成立时，判定系统稳定。选表1、表3中刀具、工件参数，切入角为120°，切出角180°，每齿进给量0.102 mm，建立三维稳定域图见图7。其中图7(a)为仅考虑第一阶模态的三维稳定图。由该图看出，临界铣削深度不仅与转速相关，亦与加工点位置相关。第一阶模态刚度在梁的两端最大，中间最小，导致在给定转速下临界铣削深度近两端处较大，中间最小。图7(b)为仅考虑第二阶模态的三维稳定图。由该图看出，第二阶模态刚度在两端及中间均较大，因此在三处附近临界铣削深度较大，但在0.75L及0.25L处模态刚度较小，表明临界铣削深度较小。图7(c)为考虑前两阶模态的三维稳定图。比较图7(d)，(e)，(f)等高线图看出，瓣图形状主要由第一阶模态决定，第二阶模态会在局部使瓣图变形。

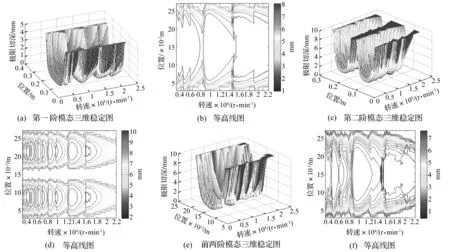
图7　三维稳定lobe图Fig.7 Three dimensional stability lobe diagram

为更好显示不同模态对铣削稳定性影响，不同模态主导的稳定性区域见图8。其中深色区域为第一阶模态占主导作用，一阶模态临界切深低于二阶模态临界铣削深度，浅色区域为第二阶模态占主导作用。由图8看出，大部分参数区间(转速与加工点)的临界铣削深度第一阶模态起决定作用，与研究铣削稳定性时只考虑工件一阶模态相符。第二阶模态在刚度较低(0.25L，0.75L)处附近，切削频率为一阶模态固有频率的1倍(转速8 715 r/min)、1.5倍(13 072 r/min)及3倍(26 145 r/min)附近起主导作用。此因在该转速附近一阶模态临界铣削深度较大。

铣削过程影响非线性最明显的为径向切深产生的铣削力断续变化，尤其当径向切深占比在5%以下时，呈现完全不同的失稳机制。而在固支梁不同位置，由于刚度变化也会呈不同的失稳方式。图9(a)为中间分岔形式，其中转速8 000 r/min，切入角170°，切出角180°。由于刚度较低，且径向切深较小，铣削力因不连续切削导致非线性作用较强烈，因此在两种因素共同作用下产生分岔形式即倍周期分岔。图9(b)为在相同条件下0.4L处分岔图，代表固支梁大部分铣削位置的分岔形式，即Hopf分岔。

图8 第一、二阶模态主导稳定区域Fig.8Thefirstandsecondmodaldominantstablearea图9分岔图(转速8000r/min)Fig.9Bifurcationdiagram(8000r/min)

4结论

针对薄壁梁模型引入等效刚度，对铣削加工过程进行等效时变刚度的时域模拟；通过综合运用庞加莱截面判断铣削时域模拟过程中的稳定性，研究不同阶模态对铣削颤振区域影响；分析薄壁梁模型在不同加工位置失稳机制及非线性特征，结论如下：

(1) 柔性工件在高速铣削状态下须考虑高阶模态影响。薄壁梁铣削的三维稳定域主要由第一阶模态决定，第二阶模态仅在局部改变瓣图；第一阶模态主要在低频占主导作用，第二阶模态主要在高频及工件两端加工区域起主导作用。

(2) 低径向切深下刚度变化会致薄壁梁铣削呈不同的失稳机制。固支梁中间刚度较小，系统发生倍周期分岔；近固支点处刚度较大，非线性特征减弱，系统呈Hopf分岔。

参 考 文 献

[1] Tobias S A, Fishwick W. The chatter of lathe tools under other cutting conditions[J]. Transactions of the ASME, 1958, 80: 1079-1088.

[2] Tobias S A, Fishwick W. Theory of regenerative machine tool chatter[J]. The Engineer, 1958,205(7):199-203.

[3] Sridhar R, Hohn R E, Long G W. A stability algorithm for the general milling process[J]. ASME Journal of Engineering for Industry, 1968, 90: 330-334.

[4] Insperger T, Stépán G. Semi-discretization method for delayed systems[J]. International Journal of Numerical Methods in Engineering, 2002, 55: 503-518.

[5] 丁烨. 铣削动力学-稳定性分析方法与应用[D].上海：上海交通大学,2011.

[6] Adetoro O B. Numerical and experimental investigation for stability lobes prediction in thin wall machining[J]. Engineering Letters, 2009, 17(4):EL_17_4_07.

[7] Bravo U, Altuzarra O, Lopez deLacalle L N, et al.Stability limits of milling considering the flexibility of the workpiece and the machine[J]. International Journal of Machine Tools and Manufacture,2005,45(15): 1669-1680.

[8] Thevenot V, Arnaud L, Dessein G. Influence of material removal on dynamic behavior ofthin walled structure in peripheral milling[J]. Machining Science and Technology, 2006,10(3): 275-287.

[9] Mane I, Gagnol V, Bouzgarrou B C, et al.Stability-based spindle speed control during flexible workpiece high-speed milling[J]. International Journal of Machine Tools & Manufacture, 2008,48(2):184-194.

[10] Tang A, Liu Z. Three-dimensional stability lobe and maximum material removal rate in end milling of thin-walled plate[J].The International Journal of Advanced Manufacturing, 2009,43(1/2):33-39.

基金项目：国家重点基础研究发展计划(973)项目(2011CB706803);国家自然科学基金(11172167)

收稿日期：2014-11-19修改稿收到日期：2015-01-07

通信作者龙新华 男，博士，教授，1972年生

中图分类号:TH212；TH213.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.008

Stability analysis for thin-walled milling processes

JIANG Yu-ping, LONG Xin-hua, MENG Guang

(Institute of Vibration, Shock, and Noise, School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

Abstract:For the milling of thin-walled structure, the effect of interaction between workpiece and tool and the position depended stiffness of workpiece can’t be ignored. The models of milling force and chip thickness were built and then the governing equations of motion of the dynamic system were presented. A time-domain simulation was issued to investigate the stability and a three dimensions stability surface was obtained in the space of spindle speed, cutting position, and axial depth of cut. The effects of vibration modes on the stability of milling processes, which is dependent on the workpiece position and spindle speed, were discussed and the position dependent mechanism of instability was explored.

Key words:milling; stability; time varying stiffness; thin-walled structure

第一作者 蒋宇平 男，硕士生，1990年生