非规则高墩曲线桥梁振动台试验研究

程麦理， 李青宁， 尹俊红， 孙建鹏， 周春娟

(西安建筑科技大学 土木工程学院，西安　710055)



非规则高墩曲线桥梁振动台试验研究

程麦理， 李青宁， 尹俊红， 孙建鹏， 周春娟

(西安建筑科技大学 土木工程学院，西安710055)

摘要：据模型相似原理及多点激励理论，对缩尺比1∶20的钢筋混凝土高墩曲线桥梁进行地震模拟振动台试验。研究高墩曲线桥梁结构在不同频谱地震波、不同峰值加速度及局部场地效应作用下高柔桥墩损伤模式及结构动力响应规律。结果表明，高柔桥墩损伤有明显的分布柔性特点，墩高差对桥墩裂缝开展及桥梁动力响应影响显著；不同频谱地震波作用下曲线桥梁结构动力响应规律各异；曲线桥梁结构动力响应峰值与地震波加速度峰值基本呈线性增长；局部地形效应使结构动力响应增大，导致曲线桥梁结构动力响应呈非线性增长；高墩曲线桥梁地震响应有明显空间性，首尾桥墩顶径向动力响应较大，易发生横桥向落梁破坏。

关键词：高墩；曲线桥梁；局部场地效应；多点激励；振动台试验；地震响应

曲线桥梁因能较好适应地形、地物限制及路线变化在我国获得广泛应用。曲线桥梁指道路中心线平面形状为曲线的桥梁结构，竖向多存在墩高差且非规则。曲线桥梁因主梁存在曲率，结构内力为弯扭耦合，计算分析较复杂。强震作用下，曲线桥梁较直线桥梁更易受损。因美国圣费南地震中曲线桥梁结构倒塌损毁，方引起对该种桥梁抗震的关注[1]，如Williams等[2]对该地震中破坏的曲线桥梁进行振动台模型试验。我国汶川地震中百花大桥第5联完全倾覆倒塌[3]，因该桥存在严重的墩高差，竖向极不规则。

Tseng等[4]用数学模型模拟方法建立考虑碰撞、屈服的伸缩缝力学模型，对曲线桥梁震害产生原因进行研究。全伟等[5]研究曲线桥结构地震输入主方向。刘保纲等[6]利用箱梁翘曲扭转理论分析翘曲扭转对曲线箱梁内力及变形影响，认为曲线桥梁结构横桥向反应较强烈。叶爱君等[7]对高桥墩进行振动台试验表明，高墩分析时P-△效应不可忽略，应对高墩进行非线性分析。

桥梁结构平面展布尺寸大、空间跨度长，使处在地形较复杂场地的桥梁在各支承处所受地震激励不一致。受地震激励影响，进行桥梁结构响应分析时应考虑局部场地效应作用[8]。王蕾[9]利用六子台阵系统研究曲线桥梁模型在一致地震动激励及多点激励下曲线桥梁的抗震性能。闫晓宇等[10]对高墩大跨连续刚构桥梁进行振动台试验，研究多点激励下桥梁的地震响应。

为探讨地震作用下非规则高墩曲线桥梁结构地震响应规律及破坏模式。本文以两跨高墩曲线连续梁桥为研究对象，设计、制作1∶20的钢筋混凝土曲线桥梁结构模型，利用改造的地震模拟振动台系统进行试验，研究高柔桥墩损伤模式，高墩曲线桥梁结构在不同频谱地震波、不同地震加速度峰值及局部地形效应作用下的结构特征点动力响应规律。以期对非规则高墩曲线桥梁结构空间动力行为及破坏过程研究提供数据与理论支持。

1试验概况

1.1模型设计

本模型上部主梁单箱单室等截面，平面为C形，下部为据等效长细比换算的柔性不等高钢筋混凝土实心桥墩。桥梁跨径为1.5 m+1.5 m。1#桥墩高1.2 m，等效长细比λ=69；2#、3#桥墩高1.45 m，等效长细比λ=83.7。1#、3#桥墩顶设有抗扭转隔震橡胶支座，2#桥墩顶设有单个固定点铰支座。各墩底均设有钢筋混凝土底座，并与振动台面可靠连接。在各桥墩顶对应处主梁均设有厚10 cm横隔板，增大曲线主梁抗扭刚度。桥梁模型各构件横截面设计尺寸、钢筋配置见图1。主梁纵筋及箍筋均用HRB335Φ6螺纹钢筋，桥墩纵筋用HRB335Φ8螺纹钢筋，箍筋用HRB335Φ6螺纹钢筋。

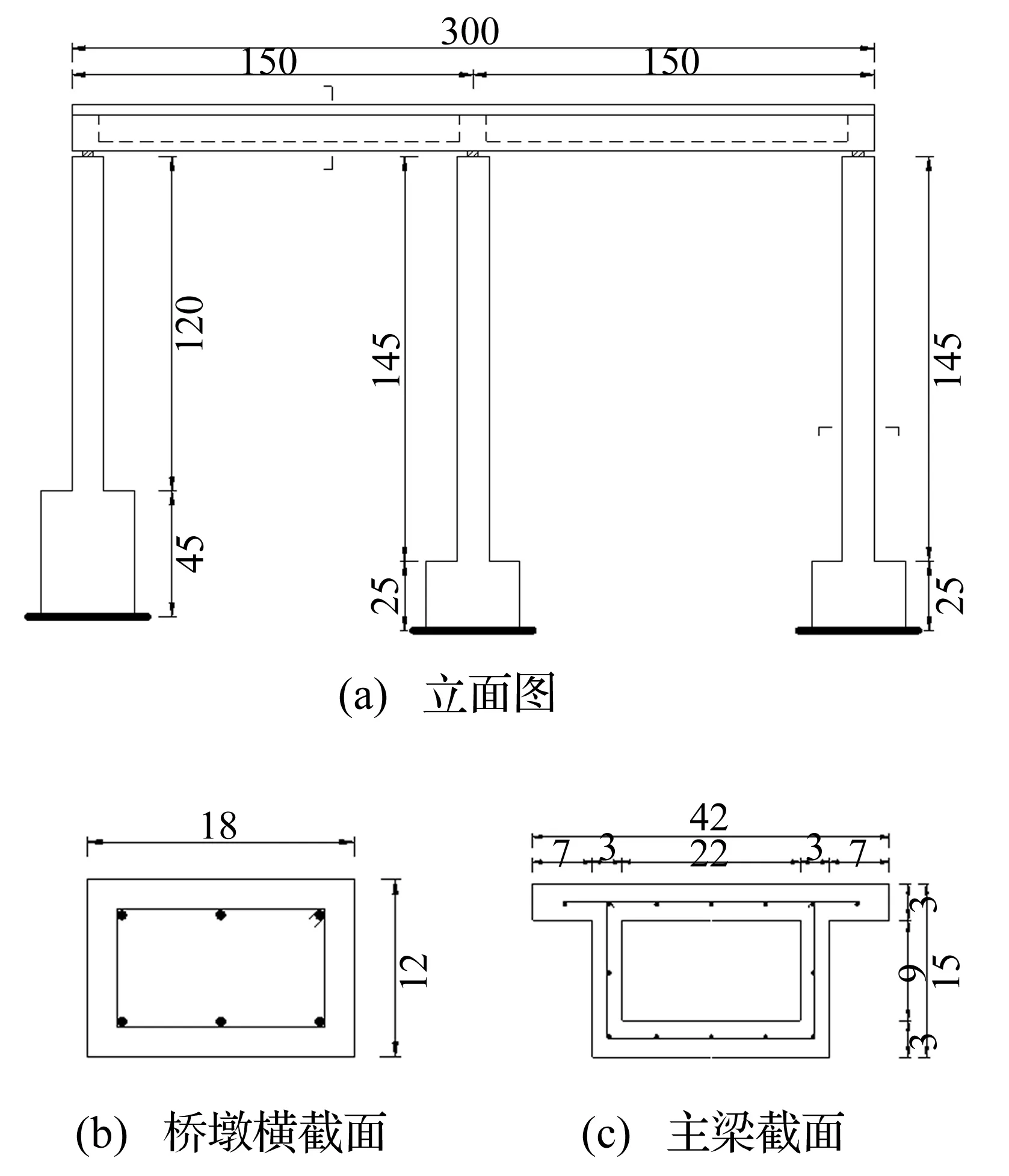
图1　曲线桥梁结构模型尺寸 (cm)Fig.1 The size of the curved bridge structure (cm)

本试验为能真实反映原型结构的动力响应，模型严格按相似理论设计计算[11]。模型主要相似关系见表1。受试验模型配重块空间限制，采用欠配重布置[12]，配重块沿模型主梁纵向摆放，模型净重418.6 kg，配重1 200 kg，共计1 618.6 kg。

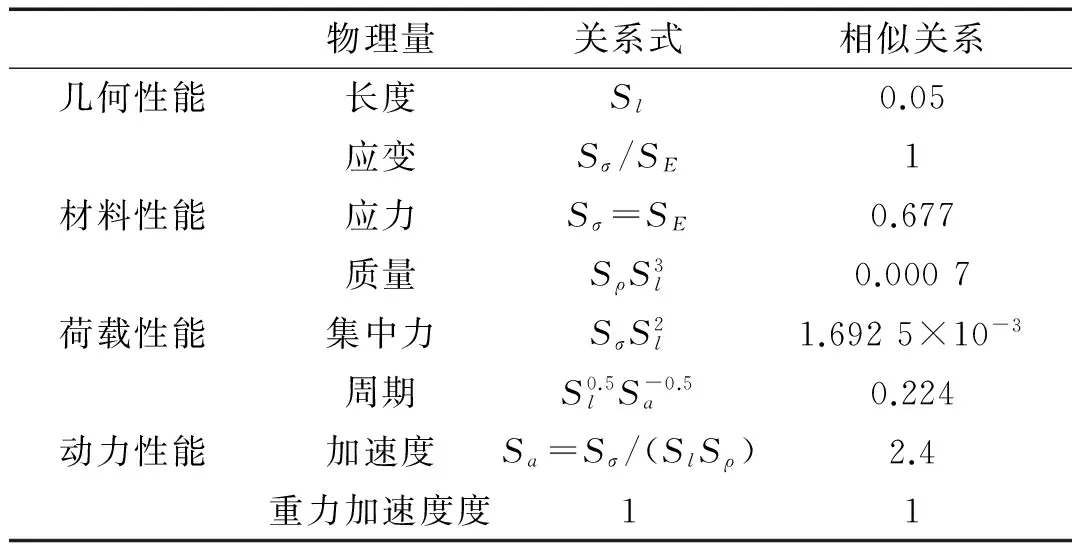
表1　模型相似比关系

图2为钢筋混凝土高墩曲线连续梁桥缩尺模型照片。主要测试各桥墩顶、主梁特征点径向及切向位移、加速度，桥墩底、墩中及主梁跨中的钢筋应变。

1.2地震动荷载输入

由于高墩曲线连续梁桥分布范围较广，可考虑不同场地类型地震波对其地震响应影响。选Ⅰ类场地地震波帝王谷波，Ⅱ类El-Centro波及兰州波，Ⅲ类Taft 波，最后试验工况为正弦波加速结构破坏，促使结构出现更多可能的破坏模式。各试验地震波加速度时程及傅里叶谱值见图3。

据地震模拟振动台试验加载原则，对结构由小到大进行地震波加载。依次对高墩曲线桥梁结构模型施加地震烈度为6度(0.05 g)、7度(0.1 g、0.15 g)、8度(0.2 g、0.3 g)及9度(0.4 g)级地震波。据加速度相似比关系，水平向设计基本地震动加速度峰值依次为120 gal、240 gal、360 gal、480 gal、720 gal及960 gal，即先施加加速度峰值120 gal的各地震波荷载，再施加240 gal的各地震波荷载，以此类推，研究分析结构特征点位移、加速度及应变的地震响应规律。

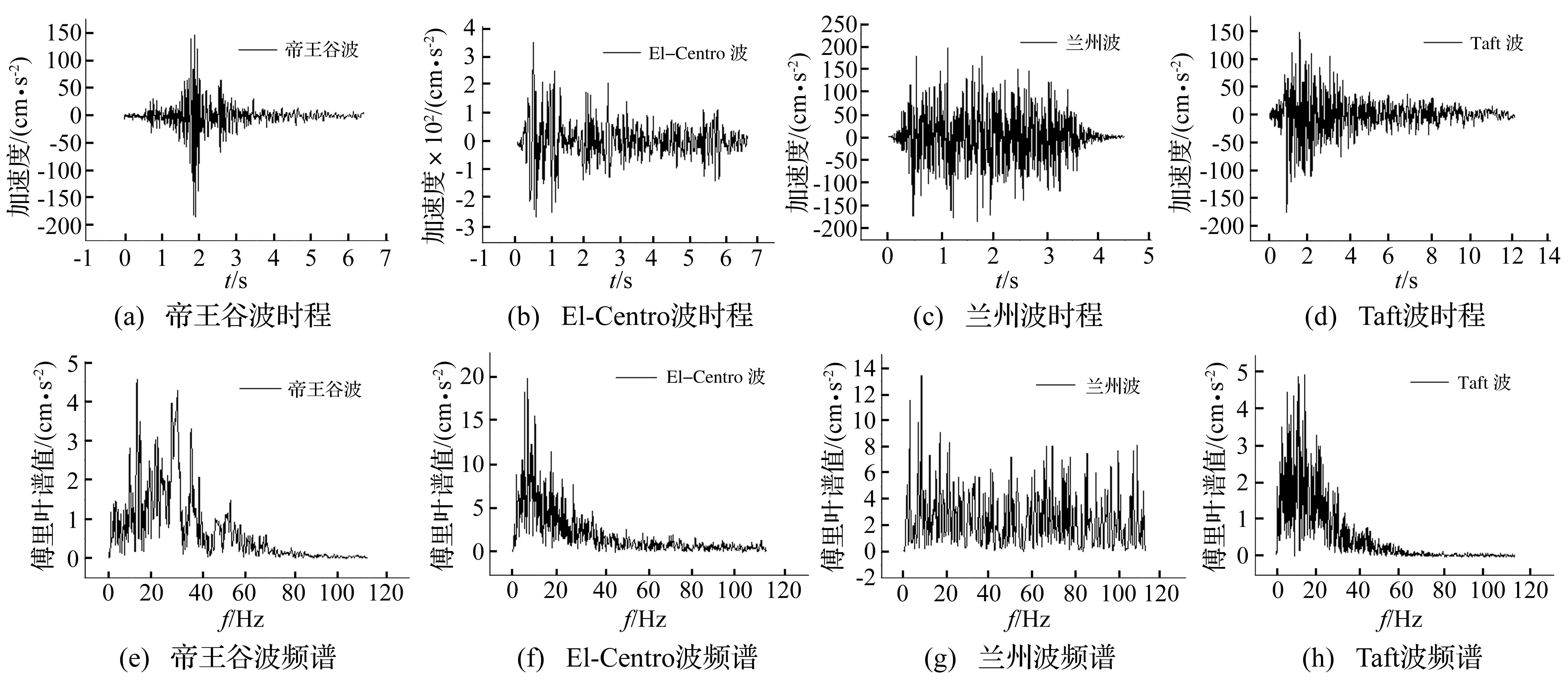
图3　试验地震波Fig.3 Earthquake waves for test

为考虑局部场地效应对曲线桥梁输入模式影响，部分工况采用非一致激励模式加载，见图4。其中χ为动力输入因数，表征因局部地形效应对大跨结构某支承点处输入地震动加速度幅值放大或缩小程度。

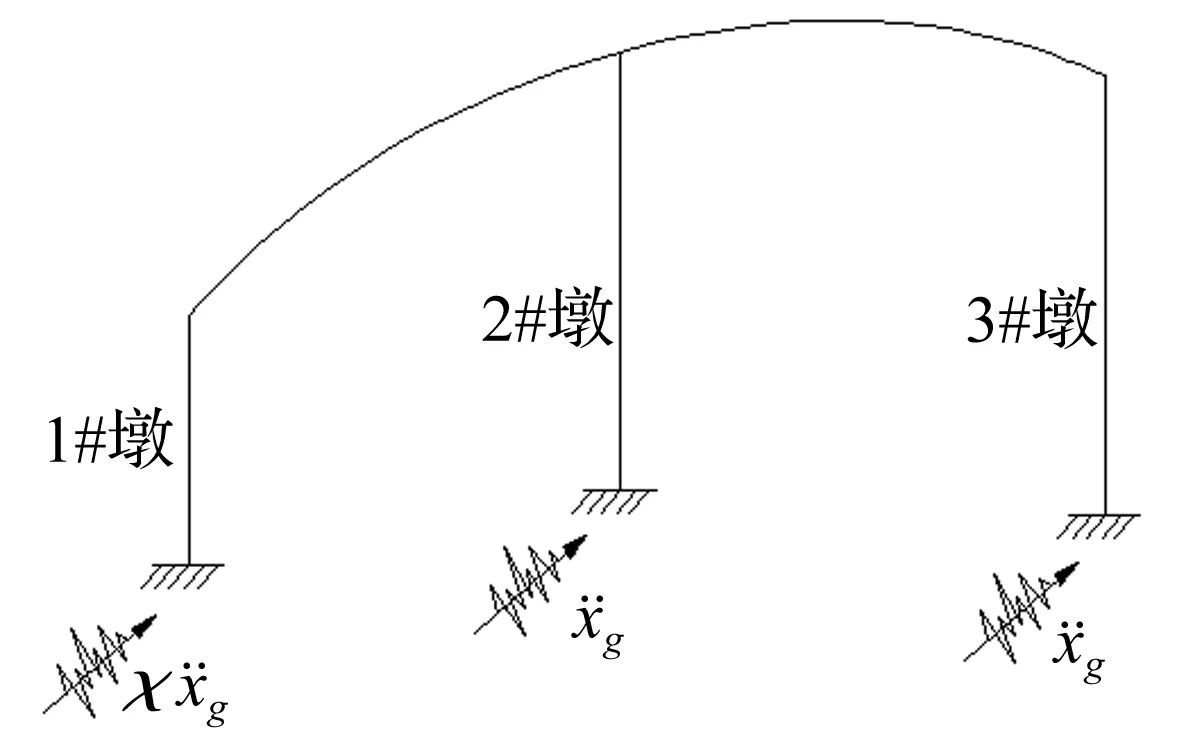
图4　地震波加载示意图Fig.4 Schematic diagram of earthquake waves loading

2曲线桥梁结构非一致激励理论

曲线桥梁建造在较复杂地形地域、进行结构抗震分析、设计时，应考虑局部地形效应对结构各支承点处输入地震波荷载差异影响[13-14]。在多点激励下结构动力运动方程与一致不同[15-16]，非一致激励输入方式结构动力方程为

(1)

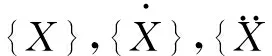
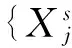
(2)

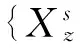
(3)

式中：γ=-[Kjj]-1[Kjz]为拟静模态矩阵，表征因支座静力位移引起的上部结构位移。

设结构阻尼力仅与其相对速度有关，对集中质量模型有[Mjz]=0；考虑支座拟静态位移与非支座节点拟静态位移关系，式(1)展开为

(4)

式(4)即为多点激励条件下桥梁结构动力方程。

3试验结果分析

桥梁结构设计思想为“强梁弱柱”，在强震荷载作用下各构件损伤中桥墩最严重。试验中对桥墩的破坏形态及动力响应测试尤其重要。

3.1试验现象及破坏形态

试验中各桥墩裂缝开展顺序及规律为：① 1#桥墩在240 gal的帝王谷波作用下首次出现裂缝，且向水平方向开展，且以横向弯曲开裂为主，主要集中在距墩底15～55 cm范围内；在正弦波作用下原有裂缝宽、深度有不同程度发展，并部分出现新裂缝。② 2#桥墩在240 gal的El-Centro波作用下现水平裂缝，主要集中在桥墩西侧中下部；正弦波作用下桥墩底部裂缝发展明显，裂缝宽、深度增大，主要分布在距墩底10～90 cm处；在长边西侧分布较多，东侧分布较少；在各荷载等级作用下均产生裂缝。③3#桥墩在240 gal帝王谷波作用下桥墩短边首次出现多条水平裂缝，且以横向弯曲开裂为主，主要集中在距墩底10～90 cm范围。所有荷载工况加载后各桥墩裂缝分布状态见图5。

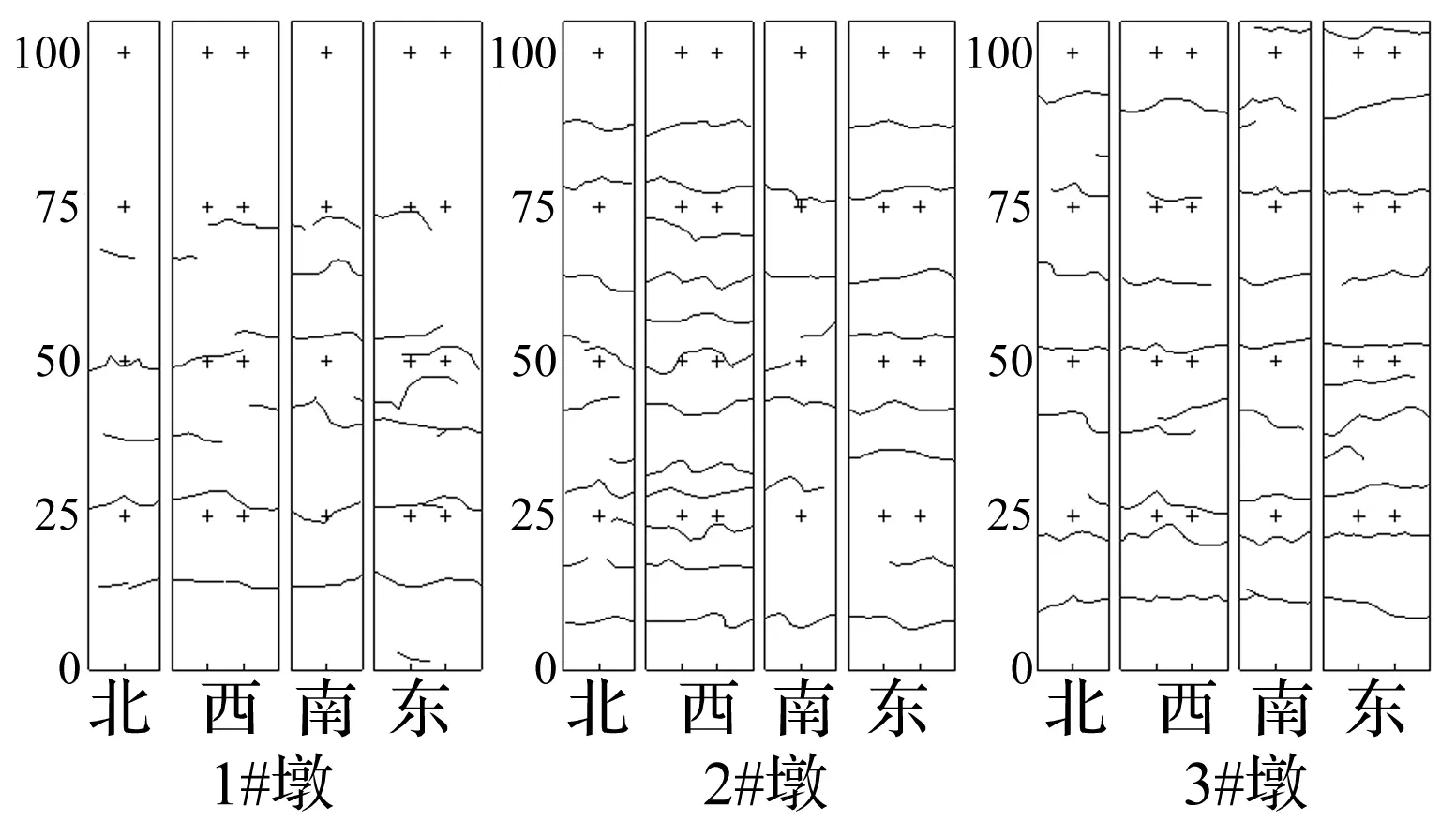
图5　桥墩裂缝分布 (单位：cm)Fig.5 Pier crack distribution (unit：cm)

对比1#、2#、3#桥墩裂缝开展范围、数量及规律可知，① 1#桥墩裂缝主要集中在距墩底0.125L～0.46L范围内，而2#、 3#桥墩裂缝主要集中在0.07L～0.625L

内。表明2#、3#桥墩较1#柔性更大，主要由桥墩高差引起。各桥墩裂缝分布范围较宽，表明进行高墩桥梁结构分析时，桥墩分布柔性不可忽略。② 2#墩较1#、3#桥墩裂缝分布更多，且开展形式以环向贯通为主。表明2#桥墩分配所得地震力最大，与曲线桥梁结构支承形式及结构特点有密切关系。

3.2试验数据分析

3.2.1不同地震波作用

为探讨不同场地地震波频谱特性对结构动力响应影响，结合试验要求对曲线桥梁结构模型依次施加360 gal峰值加速度的帝王谷波、El-Centro波、兰州波及Taft波。各桥墩顶位移、加速度响应峰值见表2，各桥墩底应变响应峰值见表3。分析表2、表3可知，① 在各类地震波作用下，各墩顶位移、加速度及墩底应变响应峰值中，1#、3#桥墩径、切向动力响应基本相当，2#桥墩切向位移达27 mm，墩底切向应变高达1 352 με，接近HRB335钢筋屈服应变，表明曲线桥梁结构主要以纵桥向振动为主，并有以2#墩为中心的平面转动，会导致曲线桥梁首尾处发生横桥向落梁的破坏模式。② 在兰州波作用下各桥墩墩顶、墩底动力响应峰值均较大。主要因兰州波频带分布较宽，幅值在各频段基本相当，地震波能量相对较大，使曲线桥梁结构发生较大动力响应。

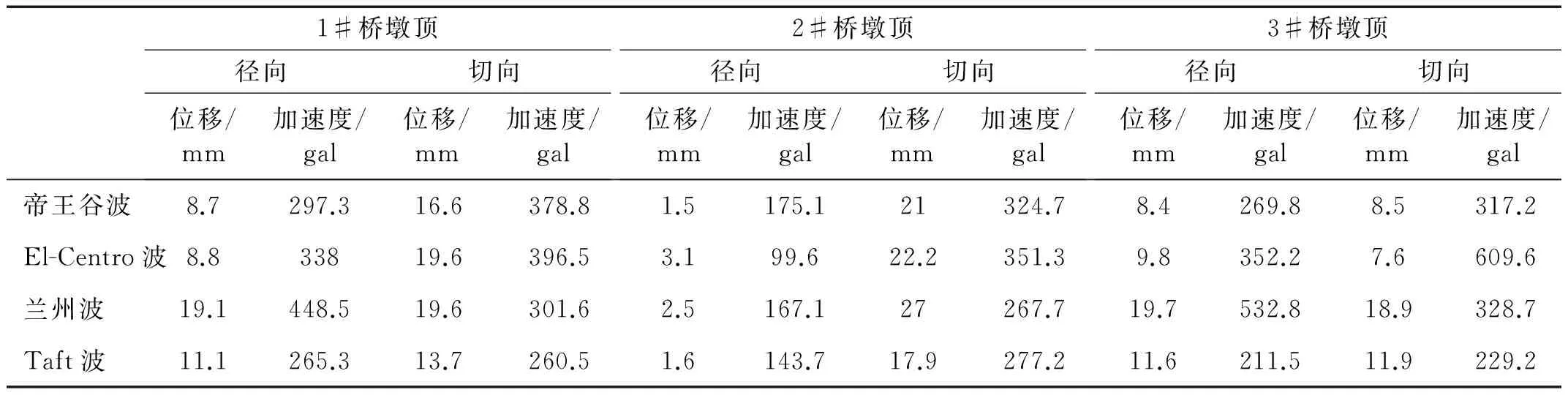
表2　不同地震波作用下桥梁结构动力响应峰值

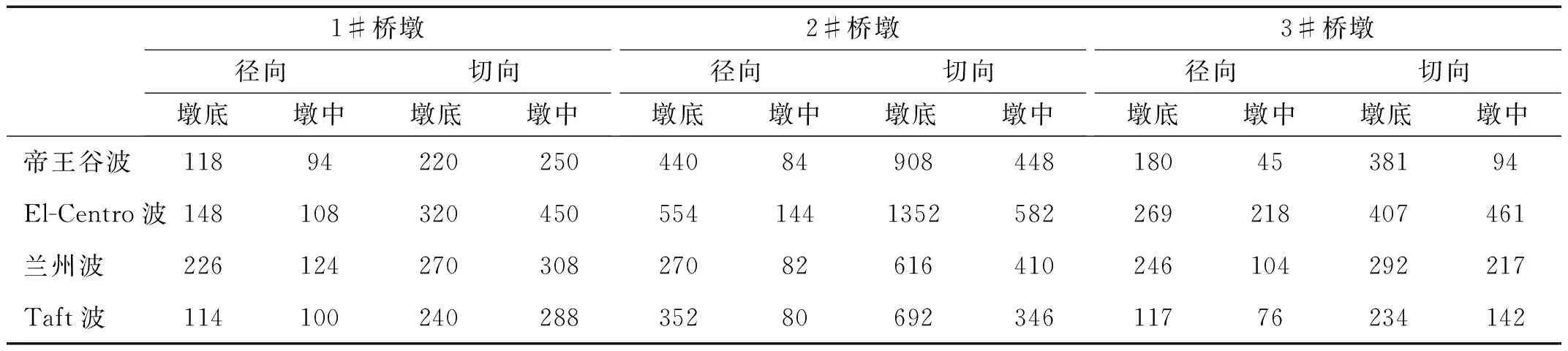
表3　桥梁结构动应变响应峰值(单位：με)

3.2.2不同地震加速度峰值作用

对曲线桥梁结构各桥墩底一致地输入地震动激励荷载，研究桥梁结构动力响应与地震加速度峰值变化间关系，探讨曲线桥梁结构动力响应与地震加速度峰值规律。曲线桥梁结构模型在Taft波120 gal、240 gal、360 gal峰值加速度作用下各桥墩顶位移及加速度响应峰值曲线见图6。由图6看出，① 各桥墩顶径、切向位移响应随地震加速度峰值增大而增大，增长趋势基本呈线性变化。主要因360 gal以下的地震荷载较小，各构件动力响应以弹性变形为主，因而结构地震响应与地震加速度峰值有线性关系。② 曲线桥梁结构以纵桥向振动为主，兼有平面转动。2#桥墩切向位移远大于径向，1#、3#桥墩径、切向位移基本相当，表明结构运动为纵桥向平动及平面转动。

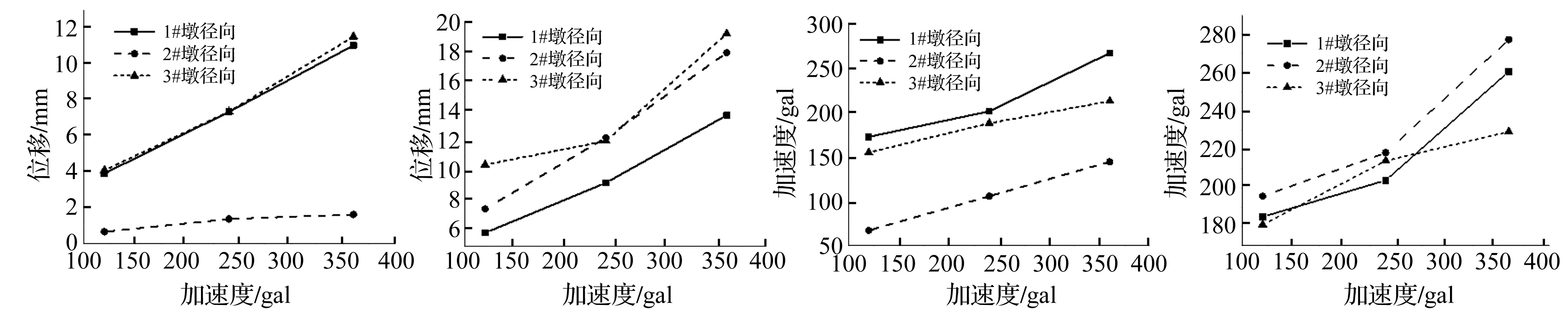
图6　不同峰值加速度作用下桥墩顶加速度响应峰值Fig.6 The acceleration response peak under the action of different acceleration

3.2.3考虑局部地形效应

为分析局部地形效应及地震加速度峰值对曲线桥梁结构动力响应影响规律，给出结构模型在480 gal、χ=1.2，720 gal、χ=1.5,960 gal、χ=2.2的Taft地震波作用下各桥墩顶位移响应时程曲线，见图7。高墩曲线桥梁模型在480 gal、720 gal及960 gal的Taft地震波作用下各桥墩顶加速度响应见表4。

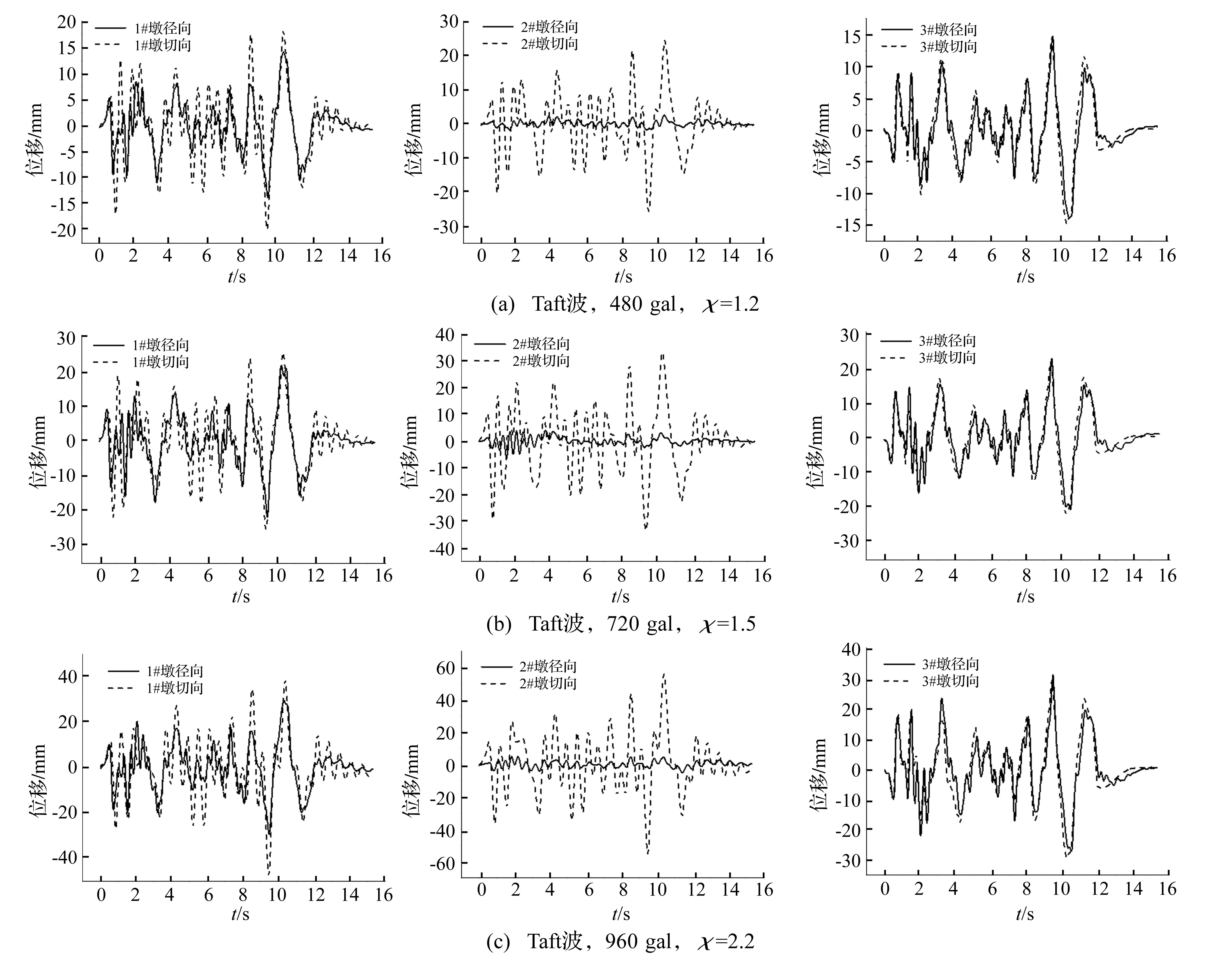
图7　桥墩顶位移响应时程曲线Fig.7 Time history curves of the displacement response

加速度幅值/gal动力输入因数χ1#墩加速度径向切向2#墩加速度径向切向3#墩加速度径向切向4801.22554641712922642717201.57307653184356375609602.21280164940950021452316

由图7、表4看出，① 各桥墩顶径向、切向位移均随加速度峰值及动力因数增大而增大，2#墩切向位移最大，表明曲线连续梁桥结构在沿桥地震波输入方向位移响应最大。② 各桥墩顶加速度随地震激励峰值加速度增大而增大，考虑局部地形效应使结构特征点加速度响应峰值增大规律呈非线性增大，加剧结构的空间动力响应。③ 1#、3#墩随地震动加速度峰值及动力因数增大呈明显非线性增大；而3#墩切向加速度响应峰值达2 316 gal，1#桥墩达1 649 gal，促使高墩曲线连续桥梁在首尾处发生横桥向落梁破坏模式。④ 因1#桥墩底输入不一致地震波荷载，导致结构在桥梁近1#墩侧出现响应差异较大的墩顶径、切向位移，3#桥墩侧有运动规律基本一致的径、切向位移。由于地震波荷载输入方向为1#、3#桥墩连线方向，与2#桥墩弱轴方向一致，故2#桥墩切向位移较大，而与荷载输入方向垂直的桥墩径向，桥墩抗弯惯性矩较大，径向位移分量较小。

4结论

据相似理论，设计制作1∶20高墩曲线连续梁桥模型进行振动台试验，研究高柔桥墩损伤模式及高墩曲线桥梁结构对地震波频谱、加速度峰值、局部地形效应等因素动力响应规律，结论如下：

(1) 进行结构动力响应分析时，应考虑高柔桥墩分布柔性，桥墩高度差对结构动力响应有一定影响。各桥墩裂缝分布范围较宽，具有明显分布柔性特点；有高度差的桥墩动力响应及裂缝开展等差异较大。

(2) 曲线桥梁结构对不同频谱地震响应各有差异。本试验的曲线桥梁结构在兰州波激励下动力响应较大，因兰州波频带较宽，且幅值在整个频带内分布基本相当，使地震波能量增大。

(3) 地震加速度峰值增大，曲线桥梁结构动力响应增大，基本呈线性增长。较小地震动荷载激励下各特征点动力响应随地震波加速度峰值增大基本呈线性增长。

(4) 局部地形效应使结构动力响应呈非线性增加，会加剧结构空间动力响应。强震荷载作用下结构特征点动力响应与局部地形效应影响有关，导致结构动力响应与地震波加速度峰值呈非线性变化。

(5) 曲线桥梁结构的动力响应呈明显空间性，易在首尾桥墩处发生横桥向落梁；沿桥纵向施加地震波荷载作用时，桥梁边墩动力响应呈明显空间性，横桥向反应较大，易发生横桥向落梁，结构振动形式为沿桥纵向平动及平面转动。

参 考 文 献

[1] 范立础. 桥梁抗震[M]. 上海：同济大学出版社，1997.

[2] Williams D, Godden W. Seismic response of long curved bridge experimental model studies[J]. Earthquake Engineering and Structural Dynamics, 1979, 7 (2): 107-128.

[3] 范立础,李建中. 汶川桥梁震害分析与抗震设计对策[J]. 公路,2009(5)：122-128.

FAN Li-chu, LI Jian-zhong. Bridge damage in wenchuan earthquake analysis and design strategies[J]. Highway, 2009(5): 122-128.

[4] Tseng W S, Penzien J. Seismic analysis of long multiple-span highway bridges [J]. Earthquake Engineering and Structural Dynamics, 1975, 4: 3-24.

[5] 全伟,李宏男. 曲线桥多维地震时程分析主方向研究[J]. 振动与冲击,2008, 27(8)：20-24.

QUAN Wei, LI Hong-nan.Research on critical angle of curved bridge in multi-dimensional earthquake time history analysis[J]. Journal of Vibration and Shock, 2008, 27(8): 20-24.

[6] 刘保纲,郭咏辉. 曲线箱梁桥的地震反应分析[J]. 土木工程学报,2003,23(10)：56-59.

LIU Bao-gang, GUO Yong-hui.Seismic analysis of curved box-girder bridge [J]. China Civil Engineering Journal, 2003, 23(10): 56-59.

[7] 叶爱君,袁万城,胡世德. 高墩振动台试验研究[J]. 同济大学学报,1996,24(6)：606-612.

YE Ai-jun, YUAN Wan-cheng, HU Shi-de. Shaking table test of a tall pier model [J]. Journal of Tongji University, 1996, 24(6):606-612.

[8] 王蕾,赵成刚,王智峰. 考虑地形影响和多点激励的大跨高墩桥地震响应分析[J]. 土木工程学报,2006,39(1)：50-53.

WANG Lei, ZHAO Cheng-gang, WANG Zhi-feng. Seismic responses analysis of continuous rigid-framed bridge with high piers considering topographic effects and multi-support excitations[J]. China Civil Engineering Journal,2006, 39(1): 50-53.

[9] 王蕾. 大跨度刚构桥地震响应分析及振动台试验研究[D]. 北京：北京交通大学，2010.

[10] 闫晓宇,李忠献,韩强,等. 多点激励下大跨度连续刚构桥地震响应振动台阵试验研究[J]. 土木工程学报，2013，46(7)：81-89.

YAN Xiao-yu, LI Zhong-xian, HAN Qiang, et al. Shaking tables test study on seismic responses of a long-span rigid-framed bridge under multi-support excitations[J]. China Civil Engineering Journal, 2013, 46(7): 81-89.

[11] 周颖,吕西林. 建筑结构振动台模型试验方法与技术[M]. 北京：科学出版社，2012.

[12] 张敏政. 地震模拟实验中相似律应用的若干问题[J]. 地震工程与工程振动,1997,17(2): 52-58.

ZHANG Min-zheng.Study on similitude laws for shaking table tests [J]. Earthquake Engineering and Engineering Vibration, 1997, 17(2): 52-58.

[13] Nuti C, Vanzi I. Influence of earthquake spatial variability on differential soil displacements and SDF system response [J].Earthquake Engineering & Structural Dynamics, 2005, 34(11):1353-1374.

[14] Lou L, Zerva A. Effects of spatially variable ground motions on the seismic response of a skewed multi-span RC highway bridge[J]. Soil Dynamics and Earthquake Engineering, 2005, 25 (7):729-740.

[15] 李忠献,史志利. 行波激励下大跨度连续刚构桥的地震反应分析[J]. 地震工程与工程振动,2003,23(2)：68-76.

LI Zhong-xian, SHI Zhi-li.Seismic response analysis for long-span continuous rigid-framed bridges under excitation of traveling waves[J]. Earthquake Engineering and Engineering Vibration, 2003, 23(2):68-76.

[16] 潘旦光,楼梦麟,范立础. 多点输入下大跨度结构地震反应分析研究现状[J]. 同济大学学报,2001,29(10)：1213-1218.

PAN Dan-guang, LOU Meng-lin, FAN Li-chu.Status of seismic response analysis of long-span structures under multiple support excitations [J]. Journal of Tongji University, 2001, 29(10):1213-1218.

基金项目：国家自然科学基金(51078306)；国家青年基金项目(51408453)；高等学校博士学科点专项科研基金(20106120110004)；陕西省自然科学基础研究计划资助项目(2013JQ7007)

收稿日期：2014-09-10修改稿收到日期：2014-12-30

通信作者李青宁 男，教授，1952年4月生

中图分类号:TU997

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.005

Shaking tables tests of irregular curved bridge with high piers

CHENG Mai-li, LI Qing-ning, YIN Jun-hong, SUN Jian-peng, ZHOU Chun-juan

(School of civil engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China)

Abstract:Based on the model similarity principle and multi-point supports excitation theory, seismic simulation tests of a scale 1:20 model of curved bridge with reinforced concrete high piers were carried out on shaking tables. The flexible high pier damage modes and the structural dynamic responses under the excitations of different seismic wave spectrums and different peak accelerations were investigated and the local site effect was taken into account. The results show that the damage mode of flexible high piers has the characteristic of notably distributed flexibility. The elevation disparity among piers significantly affect the bridge’s dynamic response and the appearance of pier cracks. The curved bridge’s dynamic response has different pattern under different spectrum seismic waves. The peak of curved bridge’s dynamic response increases linearly with the increase of the peak of seismic waves acceleration. The local site effect makes the structural dynamic response nonlinearly increase. The seismic responses of the bridge are of obvious spatiality, the radial dynamic responses at the pier tops are rather large and the damage of transverse beam falling is prone to come out.

Key words:high pier; curved bridge; local site effect; multi-support excitation; shaking tables test; seismic response

第一作者 程麦理 男，博士生，1987年6月生

邮箱：lqn952@163.com