高等代数的技巧命题探讨

郭 茜，吴贵康（成都师范学院 数学学院，四川 成都 611130）



高等代数的技巧命题探讨

郭 茜，吴贵康
（成都师范学院 数学学院，四川 成都 611130）

摘 要：学生数学思维能力训练是教学工作的重要任务，而高等代数是数学系学生必修的课程.本文从题带参数，逆转命题和一题多解三个方面讨论教师如何运用高等代数的技巧命题来提高学生数学思维能力.

关键词：高等代数；数学命题；数学教育；学生思维

高等代数是数学系学生必修的专业课，如何通过高等代数命题来反映教学中的重难点，检验学生对知识的掌握程度，是高等代数教学工作的一个重要环节；合理设计数学命题，培养学生的思维能力，是授课老师必须关注的问题.本文主要从题带参数，逆转命题和一题多解这三个方面讨论教师如何运用高等代数命题在教学中提高学生的数学思维能力.本文中相关概念参考文献［1］.

1 题带参数，训练学生思维的广阔性

思维的广阔性，主要指思路开阔，善于全面考虑问题［2］.为了培养学生思路的广阔性，可以建立带有参数的数学问题，因它随着参数的变化而变，其结果一般不确定，需要学生多方位的去分析解答，产生广泛联想.例如在设计求解线性方程组的问题时，我们可以通过在系数矩阵的设置上适当添入一些参数，让学生在解题的过程中对参数进行讨论，从而在一道试题中全面考查到线性方程组求解理论的全部知识点.

例1 求下列线性方程组的一般解，其中a，b为任意实数.

解

当b≠3时，方程组无解；

当b=3，a=2时，方程组的通解为

（-8,6,0,0）'+k1（10,-7,1,0）'+k2（8,-7,0,1）'其中 k1，k2为常数；

当b=3,a≠2时，方程组的通解为 （-8,6,0,0）'+k1（10,-7, 1,0）'其中k1为常数.

又如，求一个多项式f（x）重根的问题，如果多项式的系数只是数字，这样的题目放在大题上就会显得单薄.于是可以考虑在系数中适当的加入一些参数，做到既不过多的增加计算量，又可以让学生运用辗转相除法理论中的相关知识点对参数进行讨论，最后依据讨论的情况得到答案.

例2 求t值，使f（x）=x3-6x2+tx-8有重根.

解 因为f（x）有重根的充分必要条件是f（x）与f'（x）公共根，为此求f（x）与f'（x）的最大公因式.作辗转相除法得

于如果t≠12，则

因为如果（f（x）,f'（x）=1，则f（x）没有重根；所以，当f（x）有重根时，（f'（x）,2x-1）就必须等于x+1，即f（x）有2重根-1，此时必有f'（-1）=0，可算出t=-15.

总结以上讨论，可得当t=12时，f（x）有3重根2；当t=-15时，f（x）有2重根-1.

财务风险的防范控制一直以来都是国内外企业经营管理领域研究的重要方面。随着我国改革开放的深入和世界经济一体化的加快，而目前很多企业存在着财务结构不合理，融资不恰当等原因，面临的财务风险也逐渐的增加，因此企业财务风险的防控管理研究越来越受到学术界的关注，很多企业期望通过财务风险管理的办法来降低企业面临的财务风险，促进企业稳定、长远的快速发展。虽然很多公司在财务风险管理方面做出了一些努力，但是依旧存在着一些问题，阻碍了企业的发展。由此，本文对企业财务风险管理存在的问题展开分析，提出相应的改进策略，帮助企业提升财务风险管理水平，为企业的财务风险管理提供一些参考价值。

2 逆转命题，训练思维的逆向性

克鲁切茨基认为，组成数学能力特殊因素的基本成分中，包括了逆转心理过程能力，即从顺向的思维转到逆向思维里.所以，在教学过程中，教师应适时地将原命题逆向转换，引导学生去思考它的逆命题是否成立，并且对于不成立的情况，有没有方法使逆命题成立；或者构造一个反例.

例3设f（x），g（x），h（x）为任意多项式，且f（x）≠0，如果（f（x）,g（x）h（x）=（f（x）,h（x），那么（f（x）,g（x）=1是否成立？

解 它的原命题是如果（f（x）,g（x）=1，那么（f（x）,g（x）h（x）=（f （x）,h（x）.在证明了原命题以后，还可以进一步鼓励学生去思考它的逆命题是否成立，对此可以构造如下的反例，如f（x）= （x+3）（x-2）,g（x）=（x+3）,h（x）=（x-2）2（x+3），则（f（x）,g（x）h（x）=f（x）,h（x）= （x+3）（x-2），但是（f（x）,g（x）=（x+3）≠1.

例4 特征值都是实数的实矩阵是对称矩阵.

解 此命题是“实对称矩阵的特征值都是实数［3］”的逆命题.可以利用特征值构造矩阵，显然A的特征值就是1,5,3.它们都是实数，但是很明显A≠A'，于是逆命题不真.

3 一题多解，训练思维的发散性

思维定势对解决相同类型的问题有积极的作用，思维的灵活却能针对不同问题善于迅速地引起联想，建立联系［3］.而培养学生具有灵活性的数学思维，离不开数学题的练习.教师应鼓励学生在解题时多进行一题多解，并以此将一个问题相关的多个知识点有机的串联起来，内化形成自己的知识体系，从而达到对知识更深刻的理解和掌握.

解 这个题目是文［1］的一道习题，在［5］中提供了用数学归纳法来求解，教师在习题评讲时采用了化三角法，把行列式按第n列展开，再求解.随后学生又给出了另外一种计算方式，就是把第一行乘以1/x，加到第二行，消去-1；然后把第二行乘以1/x，加到第三行，消去-1；…；直到把第n-1行乘以1/x，加到第n行，消去-1.

例6 设P为数域，给出P3的两个子空间为

证明 P3=W1⊕W2

证明 这个例题主要是证明“和是直和”，可以利用不同的判别条件分别进行证明.这里一共展示了三种证明方式，面对不同的题目，可以选择最优的方式解答.

证法1 易知W1=L（1,0,1）,（0,0,1），W2=L（1,1,1），∀（x1,y1, z1）∈P3，有

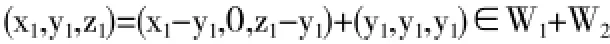
因而P3=W1+W2.又维（W1）=2，维（W2）=1，从而维（W1）+维（W2）=维（W1+W2），故P3=W1⊕W2.

证法2 对于P3=W1+W2，设（x1,y1,z1）∈W1∩W2，则有（x1, y1,z1）∈W1，可推出x1=y1=z1.由（x1,y1,z1）∈W2，可推出x1=0，因此，x1=y1=z1=0，即W1∩W2=｛0｝，从而P3=W1⊕W2.

证法3 对于P3=W1+W2，取W1的基（1，0，0），（0，0，1），取W2的基（1，1，1），显然有（1，0，0），（0，0，1），（1,1,1）为P3的基，即W1与W2的基的联合为P3=W1+W2的基，因此P3=W1⊕W2.

当然，利用高等代数去培养学生数学思维能力的方式方法还有很多，这里只能列举一部分，更多的需要在教学中不断去探索和总结.

参考文献：

〔1〕北京大学数学系前代数小组编，王萼芳石生明修订.高代代数（第四版）［M］.北京：高等教育出版社，2013.

〔2〕濮安山.中学数学教学论（修订版）［M］.哈尔滨：哈尔滨工业大学出版社，2004.

〔3〕胡典顺，徐汉文.数学教学论［M］.武汉：华中师范大学出版社，2012.

〔4〕梁武，杜玉霞，段鹏举.高等代数中的反例研究［J］.甘肃联合大学学报（自然科学版），2012，26（4）：93-95.

〔5〕王萼芳，石生明.高代代数辅导与习题解答［M］.北京：高等教育出版社，2014.

中图分类号：O151

文献标识码：A

文章编号：1673-260X（2016）06-0001-02

收稿日期：2016-03-30

基金项目：四川省教育厅自然科学基金（15ZB0346），成都师范学院科研基金项目（CS14ZB06）