学科领域中初二学生解决几何问题的图式水平及其特点研究

何荣娟（广东培正学院，广东 广州 510830）



学科领域中初二学生解决几何问题的图式水平及其特点研究

何荣娟
（广东培正学院，广东 广州 510830）

摘 要：本文采用分类测验法，两次测验来检查三种不同水平的学科领域知识、两种不同的指导方法以及高低不同的加工程度对学生图式水平的影响.结果发现：三种不同学科领域知识水平的初二学生的图式水平受到了加工程度的影响，两者之间成正相关；采用不同指导方法的被试之间存在着显著差异；题目加工程度对学生的图式水平存在着显著差异.

关键词：学科领域；图式；解决几何问题

1 问题提出

研究者对数学问题图式的研究多集中在小学生应用题的一些领域，从这些领域得到的结果是否适合于几何领域甚至是整个数学领域，其结果的适用性和推广性是有待考究的.

图式是问题解决研究领域里的重要概念，问题的解决与否直接与被试的图式水平相关.辛自强［1］在研究中发现，大部分的被试能解决几乎100%所遇到的数学方面的问题，这个研究说明学生具有问题解决所需要的图式知识.而徐青［2］通过问题分类测验发现大概有一半的被试是处在前图式水平上.被试在进行分类测验时，要做到正确的分类，是一件比较困难的事情，被试需要思考题目的深层关系，而不只是表面特征的相似，那么当被试在对题目进行加工时，加工程度的高低会在一定程度上影响被试对题目深层特征的认知，二者之间是成正比的，所以在进行分类测试时我们必须要考虑到题目加工程度的作用.

被试的学科领域知识水平是影响被试对几何问题进行表征的一个较为重要的因素.许多研究证明，丰富组被试和贫乏组被试在面对问题中的干扰信息时表现不同，那么在解决几何图形问题的过程中，学科领域知识丰富组，中等水平组以及贫乏组在解决几何问题的时候会存在着怎样的差异，领域知识和图式在学生解决几何问题的过程中是怎样的，他们之间的交互作用又是怎样的，这些问题需要我们做进一步的探讨，这些研究对于初中几何教学活动具有一定的意义，可以起到一定的引导作用.

2 研究方法

2.1 被试

从广州市某中学抽取4个自然班的学生，对学生进行学科领域知识的测验，通过采取学优者学生≥Χ+δ,学困生≤Χ-δ，而中等生是成绩介于上述两者之间，我们得到了学优生有34人，学困生有30人，中等生有106人，共有被试170名.

2.2 实验材料

实验材料主要包括：学科领域知识水平测试；与“三角形和全等三角形”两部分知识相关的几何题目6道，几何题目的设计上较全面的考虑了题目的相似性等特点（主要是文字和图）以及深层次的相似性（主要是图式性方面）.

2.3 实验设计

采用3（学科领域知识水平：高、中、低）×2（指导水平：图式性指导、概念性指导）×2（加工程度：高、低）的实验设计.因变量为图式的水平得分.

2.4 实验程序

第一阶段：对被试集体同时进行“学科领域知识水平”测试.

第二阶段：问题分类测验.其中两个班的被试在进行分类测验前进行3概念性指导，即仅对全等三角形相关的定义和概念进行回顾与复习；而另外两个班的被试则进行图式性指导，即对与全等三角形有关的解题过程或程序性知识进行指导.完毕后，发放三角形的分类测验试题A，让被试对问题进行分类，在此过程中被试无需解答，被试把分类的结果以及依据写在试卷下面的空白处，10分钟后统一收回.

第三阶段：发放分类测验试题B（试卷B与试卷A的内容是相同的但是问题的顺序是不同的），让被试对6道题目先进行解答，其中要求被试写出详细的解题步骤.完毕之后，再次对题目进行分类，这个分类可以是和之前分类的相同，也可以更改，同时也需要把分类依据写出来.解题时间控制在30分钟内.

对被试的解题过程中图式水平进行评分.计分标准为：根据题目中文字的长短或三角形图形的复杂程度与否或按图式是三角形还是平行四边形等无关因素进行分类，记0分；根据题目中文字表达所涉及的几何内容或图形中包含内容的相似来进行分类，记1分；根据题目所涉及的几何原理的相似程度来进行分类，记2分；根据题目中所涉及的关于全等三角形的解题模式或全等三角形的程序性知识进行分类，记3分.两次分类测验的成绩之和就是被试在该次研究中图式的水平.

3 结果与分析

3.1 对学科领域知识测验的有效度进行分析

本人使用的问卷是在参考刘长虹初中生数学认知结构的测量试卷的基础上，根据现在学生的现实情况进行编制.改问卷的编制主要是依据王美丽和谭顶良（2005）关于认知结构三变量的主要理论.

通过认真分析人教社九年制初一初二数学教材,选取教材当中的重点和难点,根据考纲要求中要求基础题：中等难度题：难题=7：2：1的比例，并与初二年级的级长以及一些老师进行了讨论，从而编制了测量学生学科领域知识水平的问卷.问卷主要是关于三个方面的，一方面是基础的比如某些定义，而另一些是知识点之间相关的掌握的情况，最后是整体的把握.这三个方面其实符合了考纲的要求.

我们对问卷进行了先测和正式测试，我们发现该问卷的内部一致性系数达到了0.6以上，而专家的评分者信度上达到了0.9以上，有很高的相关性，说明了该问卷的评分者信度很高.

以学生这学期的数学期中考试成绩作为效标,计算本测验分数和效标二者之间的相关系数,r=0.958,表明本测验具有很好的效标关联效度.

通过以上的分析可以说明这个学科领域知识平的问卷具有较高的可信性、有效性和科学性，是可以用于实验研究的.

3.2 加工程度不同下被试图式水平的基本情况

在解题后，高中低三种领域知识水平的学生所测量出的图式水平都明显有所提高，而相对来说低水平领域知识的被试提高趋势是最小的，其余两种水平的被试趋势都比较高，特别是高水平学科领域知识的被试.另一方面，不管是图式性指导还是概念性指导的被试解题后图式水平都有一定程度的提高，概念性指导的被试不如图式性指导的被试图式水平提高的多.

3.3 学科领域知识、指导方法和加工程度对图式水平的影响研究

为了更加深入分析领域知识水平不同的被试学生在两种指导方法下及加工程度下图式水平的不同，用方差分析的方法分析了三因数，结果见表1.

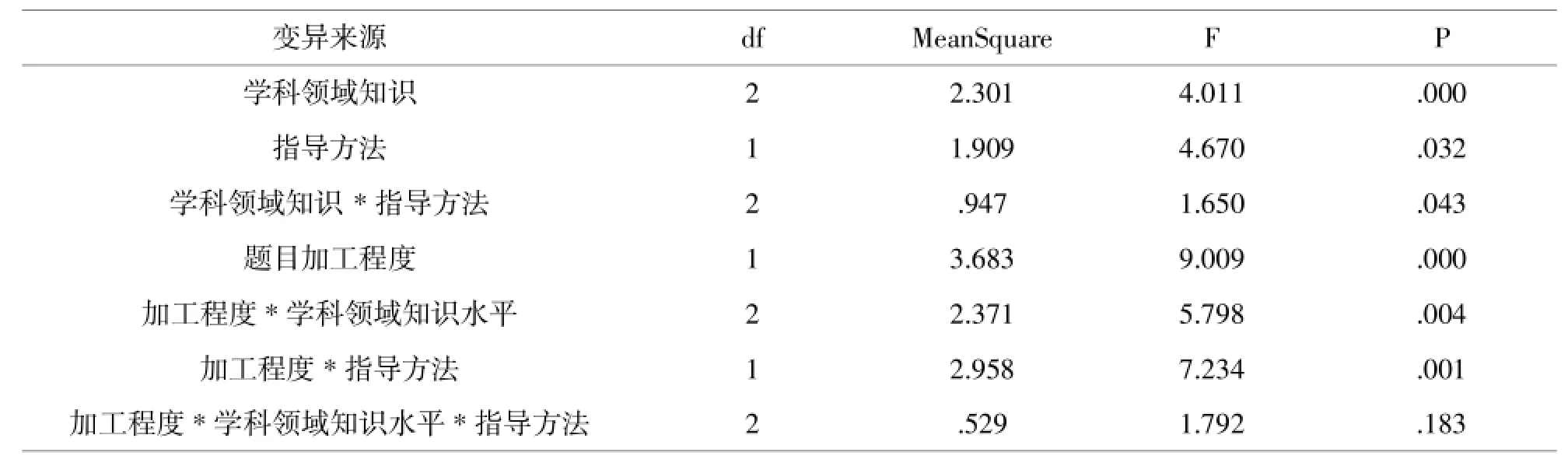
表1 学科领域知识、指导方法和加工程度对图式水平的差异研究

表1中可以看出，学科领域知识（F=4.001，P=.000＜0.05），这说明了不同学科领域知识水平的被试图式水平存在这非常显著的差异，指导方法（F=4.670,P=.032＜0.05）,这说明两种指导方法对被试的图式水平产生非常显著差异，题目的加工程度（F=9.009，P=.000＜0.05）这说明解题前后图式水平存在着非常显著的差异.题目加工程度与学科领域知识水平交互作用（P=.004＜0.05）显著，说明不同的加工程度对不同的领域知识水平学生存在着非常显著的差异；题目加工程度与指导方法的交互作用显著（P=.001＜＜0.05），这表明加工程度不同对两种不同指导方法下的被试产生了非常显著的差异.

加工程度与学科领域知识水平交互效应非常显著，因此我们对三种不同领域知识水平学生在两种不同的题目加工程度下（解题前后）图式水平得分的差异做更进一步分析，结果如表2所示.

从表2可以看出M值都是负值，这在一定程度上验证了图式水平随着加工程度的加深而增加，我们看到三种学生的sig都是等于.000＜0.01这说明了不管是学优生还是中等生以及学困生，他们对题目加工程度的提高，图式水平有着非常显著的差异.

表2 不同领域知识水平学生在图式水平得分差异的比较

因为加工程度与指导方法之间存在着非常显著的交互作用，于是对图式性指导方法和概念性指导方法下的学生的图式水平得分的差异做更进一步分析，结果见表3.

从表3中可以发现，不管是图式性指导和概念性指导在解题前后的图式水平都存在着十分显著的差异，这说明题目加工程度对于学生来说，都起到了更加深刻的认识，从而使得他们解题前后的图式水平差异大.

表3 两种指导方法下的学生图式水平得分差异的比较

4 讨论

我们知道问题的成功解决依赖于对问题的有效表征，而在问题解决过程中被试已有的认知结构中的图式知识影响着被试对问题的表征.个体很多时候在解题中出现错误不是由于被试他的基础的计算能力而是由于他使用了错误的问题图式，由此可见个体本身所具有的问题图式对问题解决的重要影响.题目加工程度的加深对于所有的学生来说都有着重要的影响，学生之前图式水平差或者不够丰富，可以通过对问题的不断的加工来进行补救，这也就是我们常说的勤能补拙.

4.1 题目加工程度对学生图式水平的影响

我们知道几何题包含了文字和数字符号以及图形的信息，那么在分类的时候我们很容易就根据文字或图形对他们进行分类，特别是问题的表面特征很相似时，我们很容易忽略深层次的东西［3］.当时间相对较少时学生集中在表面特征上，但是想要解决问题，没有深层次的东西是不行的.我们发现当学生对问题进行了解答之后对问题的深层的东西有了更全面的认知，当再次做分类任务时，他们的图式水平明显提高了.

4.2 在全等三角形的几何问题中不同的指导方法对图式水平的影响

解题后学生的图式水平有提高，但是整体提高的不多，整体图式水平还是比较低，学生对问题的深层认识还是不够，整体比较分散.Hans等人［4］的研究证明，适当的线索提示对问题图式的激活是很重要的，同时对图式的归纳也是更容易.图式性指导的进行是为了使被试内在程序性知识得到有效的梳理，而解题案例的讲解则有利于学生激活相关的线索，有利于问题的解决.而概念性指导只是对相关概念和定理的回顾和复习，虽然可以让学生更加准确的掌握知识点，但是学生很多时候分析题目还是流于表面，所以此时分类的图式水平是明显低于图式性指导的图式水平的，但是在经过解答之后我们发现被试的图式水平得到了较大的提高.这说明了对问题的进一步分析有利于我们对题目深层问题的认识.

这一结果提示我们在教学过程中，教师除了对基本定理和概念的掌握外，还应该强调对问题的解题思路，思维方法等深层次的内容进行记忆，并把这些内容进行概括，使得他们在以后类似的题目中具有推广性，有利于问题的解决.同时我们发现对问题的加工也有利于对问题的认识，那么在平常的数学教学中，我们要多练，多做不同类型的题目，同时要总结，这样有利于在以后的解题中激活相关的内容.

4.3 学科领域知识水平学生在两种题目加工水平和两种指导方法下表现出图式水平的特点

学科领域知识水平是影响学生问题解决的重要因素，尤其是在理科知识的学习过程中，不同的学科领域知识水平学生的认知方面存在着差异.学科领域知识水平的不同在信息的选择和组织上都表现出一定的差异.

学优生在面对复杂问题时表现为会利用已有的图式，而中等生次之，学困生则最差.在两次分类测验中发现三种学科领域知识水平的学生在解题前后图式水平差异存在着显著，而后测验的图式水平比前面测的图式水平更高.这个结论在一定程度上是张夏雨［5］、俞国良［6］的研究的进一步细化.

5 结论

三种不同学科领域知识水平的学生的图式水平受到了题目加工程度的影响，在加工程度较低时图式水平较低，在加工程度较高时图式水平更高，对于进行图式性指导的学生与进行概念性指导的学生之间存在着显著差异，不管是那种指导方法的学生，题目加工程度对学生的图式水平都存在着显著差异.

参考文献：

〔1〕辛自强.社会认知复杂性的量化指标及其关系［J］.心理科学，2007（04）.

〔2〕徐青.几何问题解决的图式水平及其特点研究［J］.安阳师范学院学报，2012（1）：134-137.

〔3〕EgbertG.Harskamp，CorJ.M.Suhre.Improving mathematical problem solving：A computerized approach ［J］.Computers in Human Behavior，2006，（22）：801-815.

〔4〕Hans，G.K.Humme，l Rob J.Nadolsk.i Cuing for schema construction：Designing problem solving multimediapracticals.ContemporaryEducationalPsychology，2002（27）：229-249.

〔5〕张夏雨，喻平.不同学业水平学生数学问题图式的差异性研究［J］.数学教育学报，2011（2）.

〔6〕曾盼盼，俞国良.小学生视觉—空间表征类型和数学问题解决的研究［J］.心理科学，2003，26（2）：268-271.

中图分类号：G633.6

文献标识码：A

文章编号：1673-260X（2016）06-0271-03

收稿日期：2016-03-15