基于显式动力学的推力滚针轴承振动分析与试验研究

余光伟，王嘉鑫，陈晓阳，卢俊，黄迪山

(上海大学 机电工程与自动化学院，上海 200072)

推力滚针轴承因安装所需轴向空间小等优点，广泛应用于机械电子仪器、电动工具、汽车变速器等机械设备中[1]。随着对机械动力性能和噪声要求的提高，推力滚针轴承的振动性能显得非常重要,故有必要进行专门分析。

基于轴承运转时滚针与滚道接触处产生的能量损失最小的假设，推导出推力滚针轴承各零件速度的计算方法。以AXK2542推力滚针轴承为例，在ANSYS/LS-DYNA中建立模型，并采用显式动力学有限元法对其进行仿真分析，得到了轴承各零件的速度，与理论计算结果相比误差较小。通过该有限元法分析了转速、轴向载荷对推力滚针轴承振动加速度的影响，并进行了试验验证。说明采用ANSYS/LS-DYNA软件建立的有限元模型可用于对推力滚针轴承的振动分析。

1 显式动力学

ANSYS/LS-DYNA是一个以显式动力学为主，隐式动力学为辅的有限元求解器。显式动力学采用中心差分方法，既不需要求解切线刚度，也不需要进行平衡迭代，可节省大量计算资源和时间。系统的求解方程为

(1)

中心差分法解的稳定条件为

(2)

式中：Δter为临界时间间隔；Tn为有限元系统的最小固有振动周期。

2 轴承各零件速度计算模型

滚针与垫圈速度示意图如图1所示，假设轴承座圈固定，轴圈以角速度ωh旋转，保持架和滚针公转角速度为ωc，滚针自转角速度为ωr。r为滚针半径，re和ri分别为滚针两端面到轴承轴线的距离。

(a) 滚针与轴圈

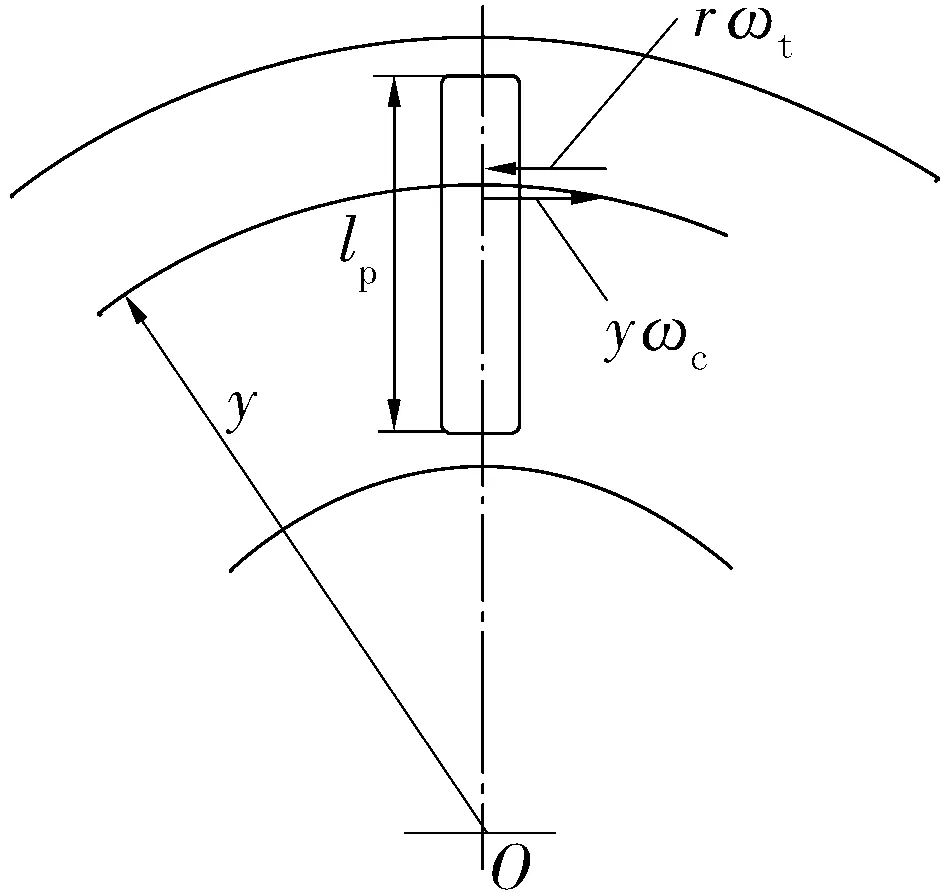
(b) 滚针与座圈

由图1可知，在半径y处滚针与轴圈接触面的相对滑动速度为

Sr1=yωh-(yωc+rωr)，

(3)

由于滚针与轴圈和座圈之间的相对滑动造成的能量损失[2]为

(4)

式中：Z为滚针数；μ为滚针与轴圈和座圈之间的动摩擦因数；pm为平均接触应力；b为接触椭圆半宽。

根据Hertz理论得[3]

Q1=Fa/Z,

(5)

式中：Q1为单个滚针上的载荷；Fa为轴向载荷；lp为滚针有效长度。

由(4)式、(5)式得

(6)

同理可得，滚针与座圈接触面之间的相对滑动速度为

Sr2=yωc-rωr，

(7)

能量损失为

(8)

则总能量损失为

(9)

式中：lg为滚针和垫圈之间无相对滑动处到轴承轴线的距离。

滚针的自转角速度和公转角速度ωr取决于能量损失Et，当能量损失最小时

(10)

由(10)式可得

(11)

由此可见，无相对滑动的位置位于滚针中点。将(11)式代入(3)式和(7)式得

(12)

(13)

3 有限元模型

3.1 建立模型

以AXK2542推力滚针轴承为例，其主要结构参数见表1。

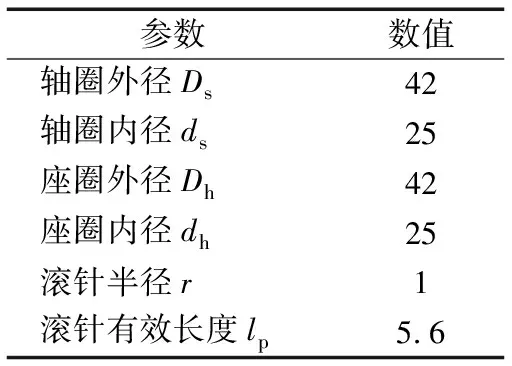
表1 主要结构参数

采用自下而上的方式建立推力滚针轴承的几何模型,并对模型做如下简化：1)忽略轴承的倒角和边棱对内部应力的影响；2)不考虑垫圈波纹度和表面粗糙度的影响；3)不考虑润滑油膜的影响。将几何模型通过标准图形输入接口导入到ANSYS/LS-DYNA前处理器中，有限元单元选用Solid164，采用扫略分网、映射分网和自由分网相结合的方式划分网格。轴圈、座圈上表面设置为Shell163单元，以便施加转速和载荷。

轴圈、座圈和滚针采用六面体单元，保持架采用四面体单元。建立的有限元模型如图2所示。

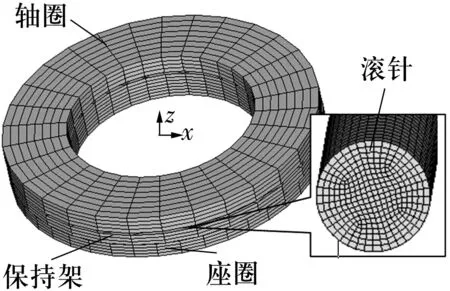
图2 推力滚针轴承有限元模型

3.2 材料参数

由于轴承塑性变形很小，因此将轴圈、座圈和滚针均设为线弹性材料。在仿真模型中，假设轴圈、座圈和滚针材料[4]均为GCr15钢，保持架材料为3Cr13钢，其材料力学参数见表2。

表2 材料力学参数

3.3 载荷与约束

参照试验，压力简化为均布压力，同转速一起施加在轴圈上表面，座圈设为全约束。

3.4 接触与边界条件

推力滚针轴承运转过程中，滚针与轴圈、座圈之间的接触设为自动面-面接触，静摩擦因数均为0.35[5]，动摩擦因数均为0.16；保持架与滚针、 轴圈和座圈之间的接触设为自动面-面接触，静摩擦因数均为0.002，动摩擦因数均为0.001；座圈与底座之间的接触设为自动面-面接触，静摩擦因数均为0.35，动摩擦因数均为0.16。试验测量推力滚针轴承振动时，轴圈连接在刚性很大的轴上，座圈固定在轴承座上，由于Solid164单元没有旋转自由度，因此将轴圈上表面和座圈下表面设置为刚性面，模拟轴承的边界条件。

4 试验验证

推力滚针轴承测振仪如图3所示，被测轴承置于底座上，通过气压装置使其与主轴压紧，主轴带动轴圈转动，压电加速度传感器的传振杆与座圈底面接触测量振动，将被测轴承的振动加速度信号转换成电信号，经信号调理模块放大、滤波后，传至数据采集卡，再由工控机进行分析处理。通过调节主轴电动机转速来改变轴承转速，通过双螺母调节弹簧压缩量来改变轴向载荷。

1—底座；2—主轴；3—工控机；4—信号调理模块；5—传感器；6—双螺母

5 结果分析

5.1 速度分析

对轴圈施加400 N的轴向载荷，转速为1 800 r/min，为方便与理论值对比，取轴圈外侧面节点49 726、保持架外侧面节点43 540和滚针外端面边沿节点300(图4)，各节点的速度曲线如图5所示。

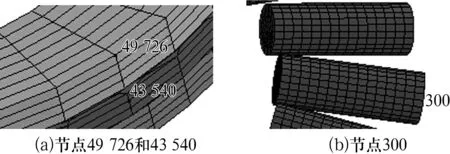
图4 节点49 726，43 540和300的位置

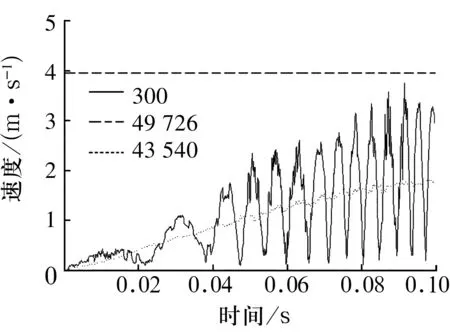
图5 各节点速度

由图5可知，轴圈速度保持恒定，保持架转速随时间增长而增大，经过约0.08 s后稳定，滚针外端面边沿的线速度呈周期性变化。

轴承各零件速度计算值与仿真值对比见表3，由表可知，仿真值与理论计算值相差不大。

表3 轴承零件速度计算值与仿真值对比

5.2 振动加速度分析

选取座圈底面边沿的节点40 916(图6)，当施加在轴圈上的轴向载荷为400 N、转速为1 800 r/min时，节点加速度曲线如图7所示。

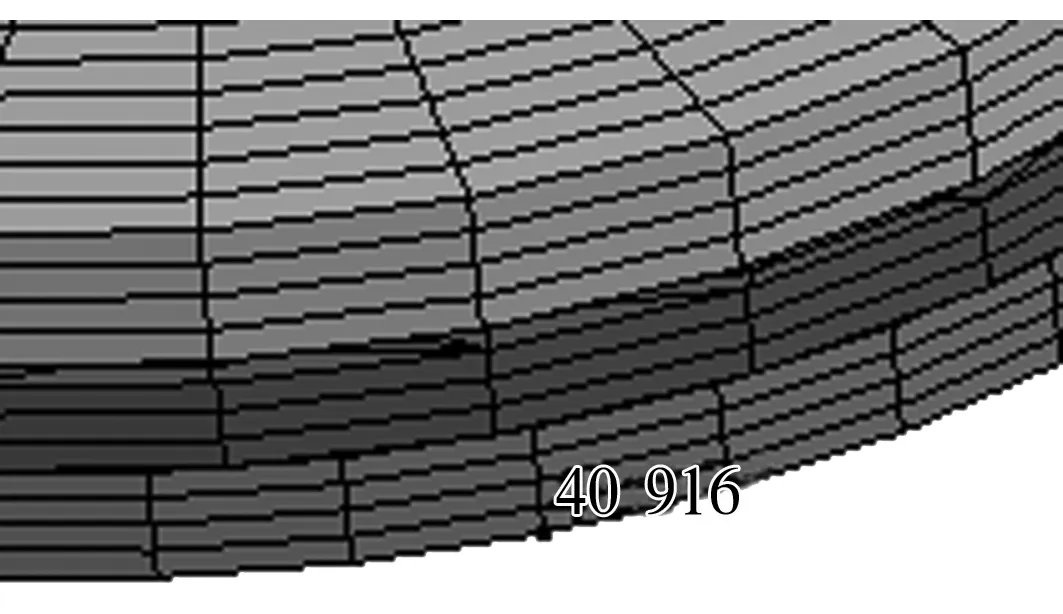
图6 节点40 916的位置

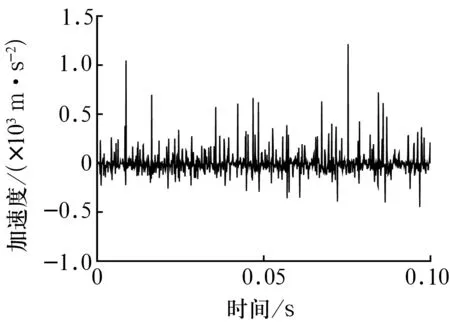
图7 节点40 916的加速度

轴承振动加速度值[6]为

(14)

式中：a为振动加速度均方根值；g为重力加速度。

5.2.1 转速对振动加速度的影响

轴向载荷为400 N时，轴承振动加速度随转速的变化如图8所示。由图8可知，随转速增大，振动加速度的仿真值和测量值均无明显变化，仿真值比测量值小约4 dB。其原因为：1)仿真时忽略了垫圈波纹度和材料表面粗糙度等工艺参数的影响;2)试验测试系统中不可避免地存在噪声干扰。

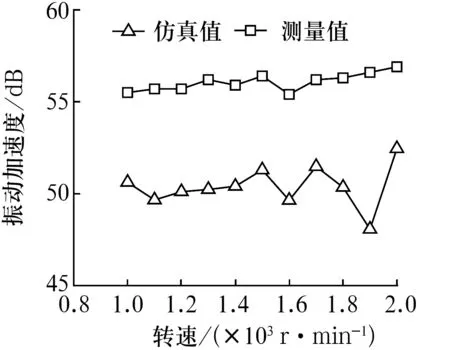
图8 振动加速度随转速的变化

5.2.2 轴向载荷对振动加速度的影响

转速为1 800 r/min时，轴承振动加速度随轴向载荷的变化如图9所示。由图9可知，随轴向载荷增大，轴承振动加速度也增大，仿真值的增幅明显大于测量值，这是由于仿真时忽略了润滑油膜的影响，在实际工况中，滚针与滚道之间会形成润滑油膜，可以起到减振隔振的作用，缓解了轴向载荷对振动加速度的影响。

图9 振动加速度随轴向载荷的变化

5.2.3 滚针个数对振动加速度影响

轴向载荷400 N、转速1 800 r/min时，轴承振动加速度随滚针个数的变化如图10所示。由图10可知，当滚针个数小于35时，轴承振动加速度随着滚针个数的增加而减小，这是由于滚针个数增多使得单个滚针所受轴向载荷减小；但当滚针个数为40时，其振动加速度值有所上升，这是因为随着滚针个数的增多，滚针与保持架间的耦合作用增强，滚针与保持架接触频繁[7]，导致轴承的振动增大。

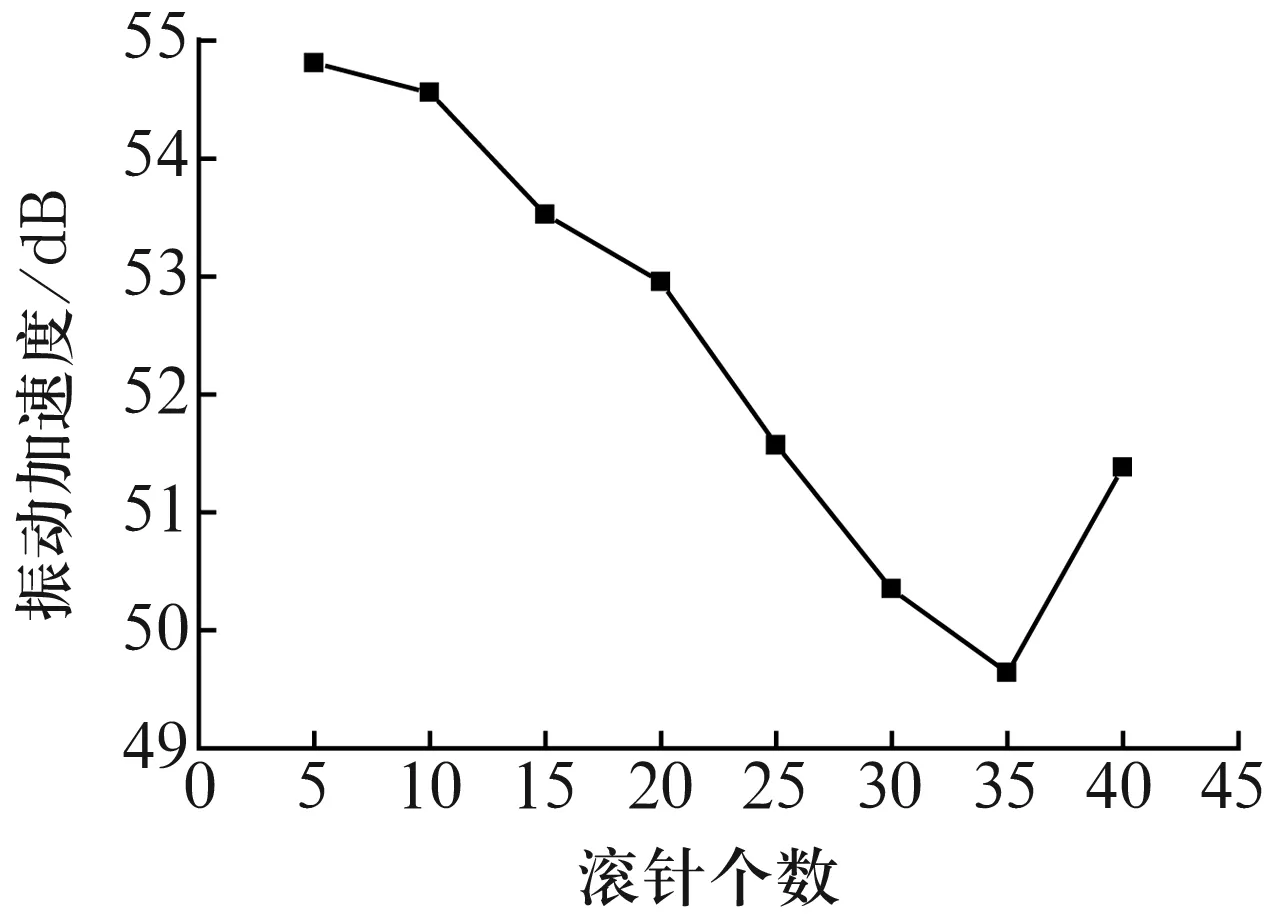
图10 振动加速度随滚针个数的变化

5.2.4 滚针直径对振动加速度的影响

轴向载荷400 N、转速1 800 r/min时，轴承振动加速度随滚针直径的变化如图11所示。由图11可知，随着滚针直径的增大，轴承的振动加速度也增大。

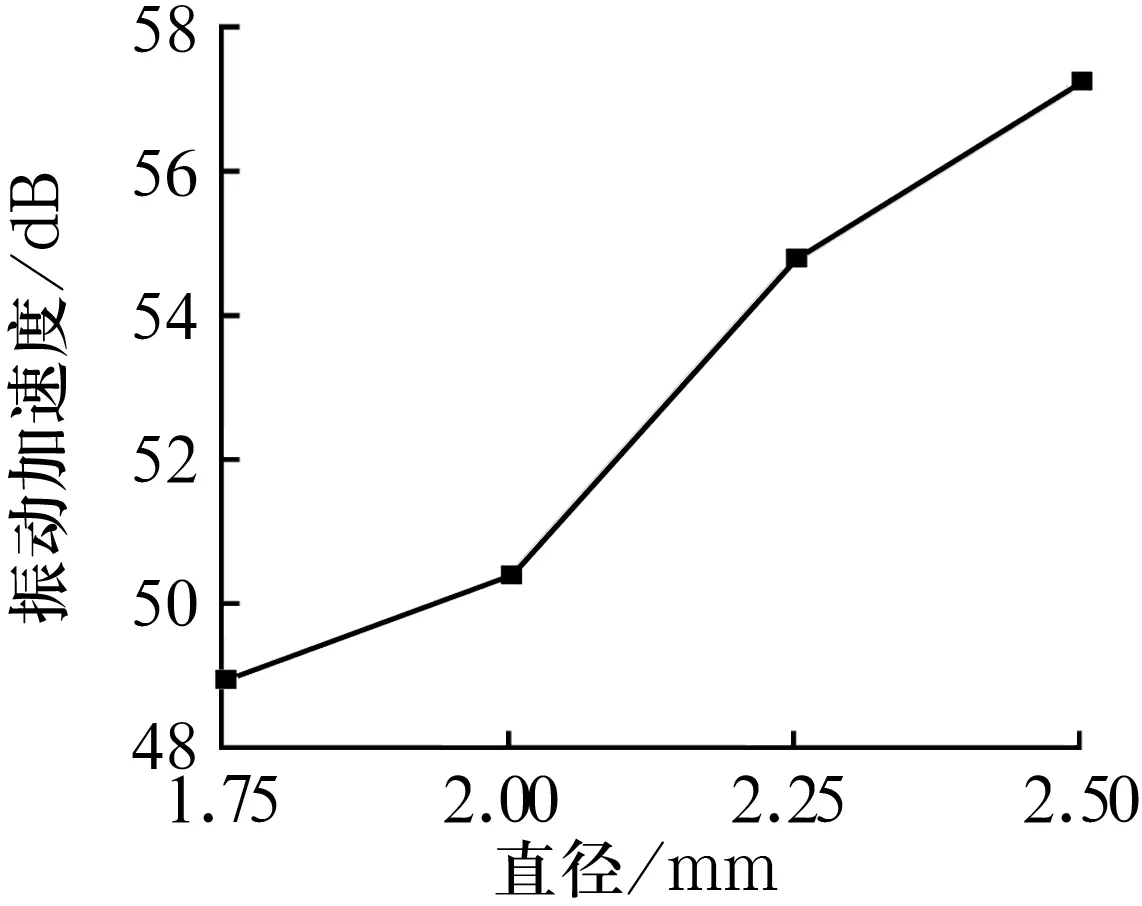
图11 振动加速度随滚针直径的变化

6 结论

1)在所研究的速度范围内，转速对推力滚针轴承的振动加速度影响很小。

2)随轴向载荷的增大，推力滚针轴承的振动加速度也增大。

3)存在一个最佳的滚针个数，使得推力滚针轴承的振动加速度最小。

4)随滚针直径的增大，推力滚针轴承的振动加速度也增大。