变分模态分解在轴承故障诊断中的应用
2016-07-25岳应娟孙钢蔡艳平刘长江张世雄
岳应娟,孙钢,蔡艳平,刘长江,张世雄
(第二炮兵工程学院,西安 710025)
轴承振动信号具有非线性、非平稳的特性,传统的信号分析方法难以处理,经验模态分解(Empirical Mode Decomposition,EMD)[1-5]能够较好地处理此类信号,但也存在端点效应、包络拟合及模态混叠等问题[6-9],仍需进一步优化。
变分模态分解(Variational Mode Decomposition,VMD)[10]是一种新的自适应信号处理方法,其本质上是多个自适应维纳滤波组,有着良好的噪声鲁棒性。VMD可实现信号频域内各个分量的自适应剖分,有效克服EMD算法分解过程中的模态混叠及伪分量等不足,比EMD有更强的噪声鲁棒性及较小的端点效应。因此,尝试将VMD与谱峭度相结合,用于轴承故障信号的诊断。
1 变分模态分解算法
VMD通过迭代搜寻变分模型的最优解来确定每个本征模态分量(Intrinsic Mode Function, IMF)的中心频率和带宽,实现信号频域和各个IMF的自适应剖分,是一种完全非递归的信号分解方法。
信号经过VMD处理被分解成一系列IMF,每个IMF都可以表示为一个调幅-调频uk(t)信号,表达式为
uk(t)=Ak(t)cos(φk(t)) ,
(1)

为估算每个IMF的带宽,可分3个步骤:1)通过 Hilbert 变换计算与每一个模态uk(t)相关的解析信号;2)通过加入指数项调整各自估计的中心频率,将uk(t)的频谱变换到基带上;3)对解调信号进行 H1高斯平滑,估计带宽。
假设信号经VMD处理后分解为K个IMF,则变分约束模型为
(2)
式中:δ(t)为Dirac分布;*表示卷积;k=1,2,…,K;f为原始信号。
为求取变分约束模型的最优解,引入二次罚函数项α和Lagrange乘子λ可得
L({uk},{ωk},λ)=
(3)
VMD采用乘法算子交替的方法求取上述变分约束模型,得到最优解将信号分解成为K个窄带IMF,其实现流程如下:
2)令n=n+1,执行整个循环。
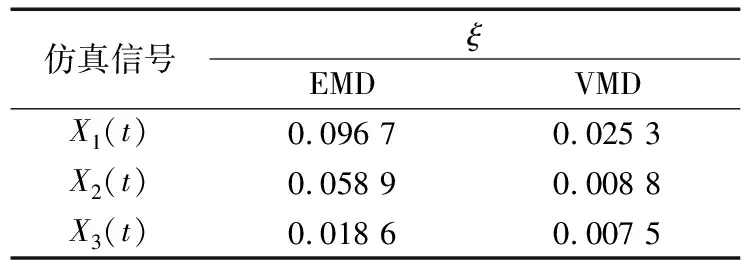
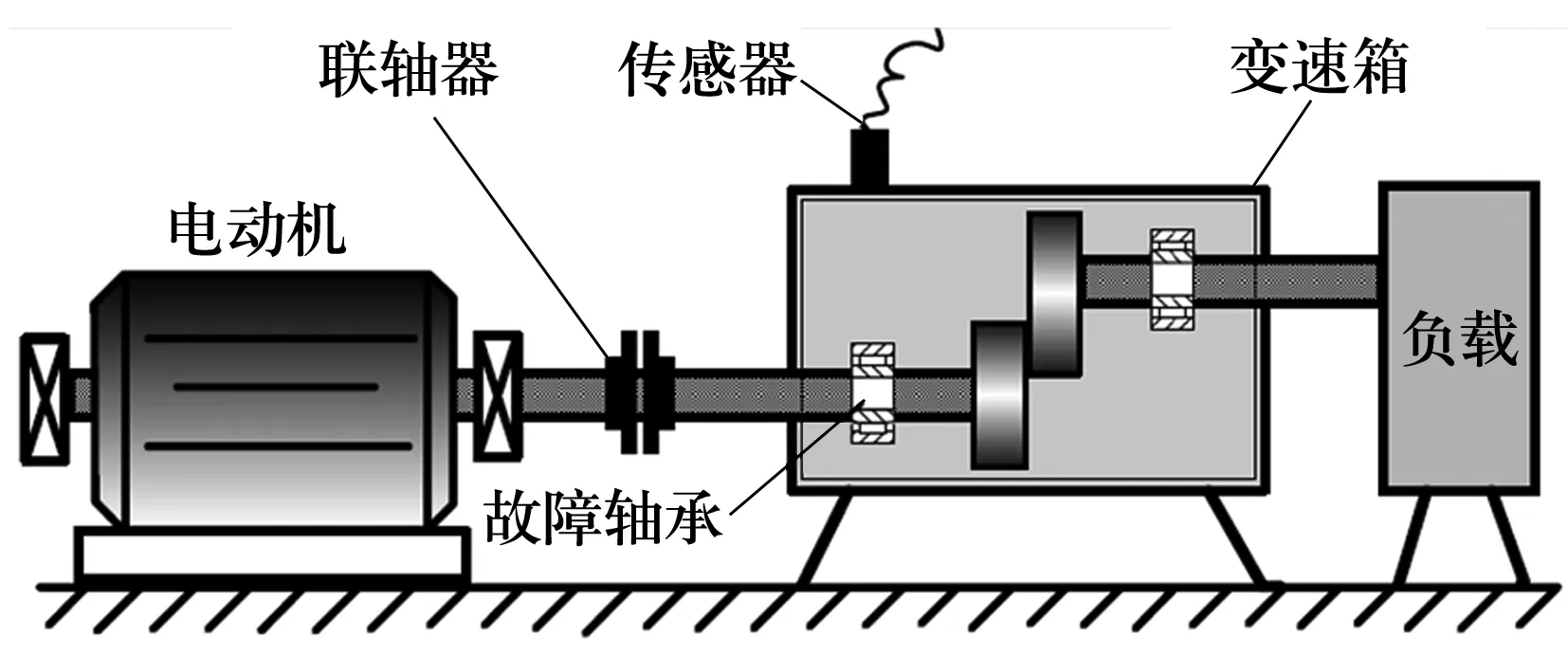
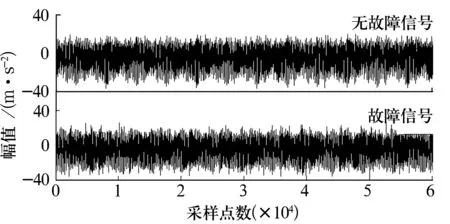
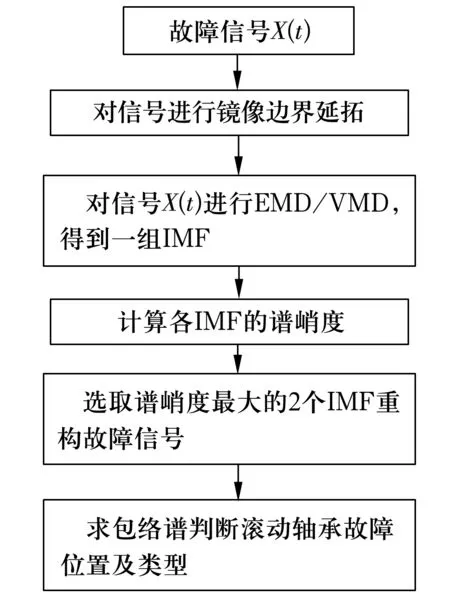
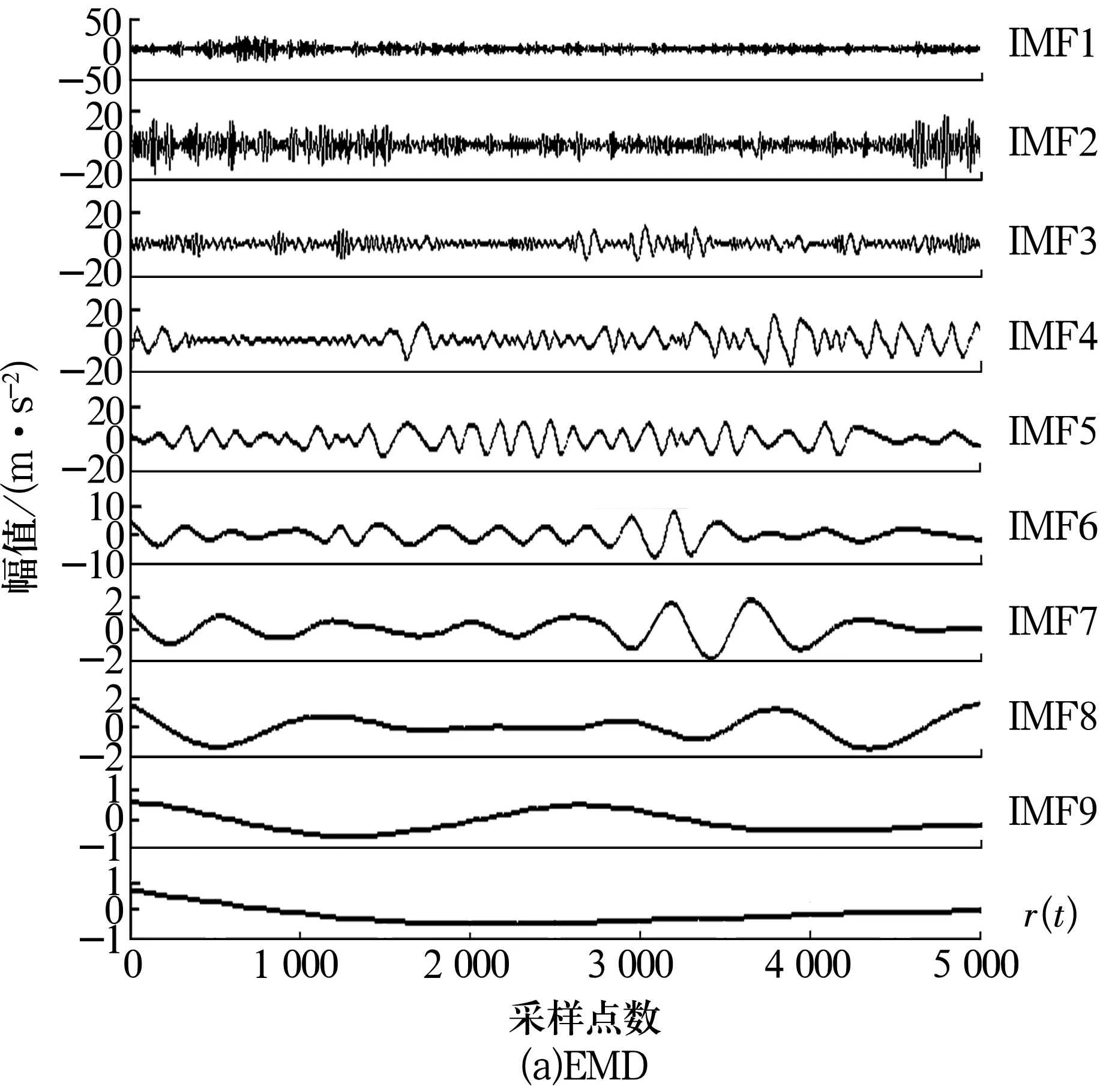
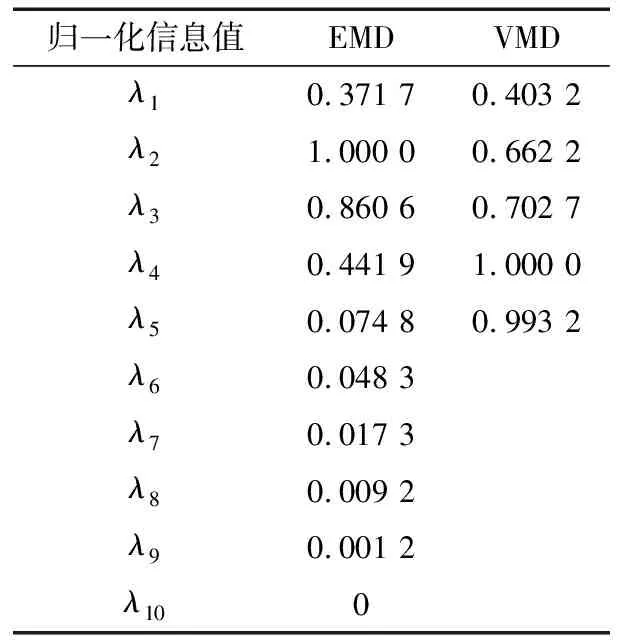
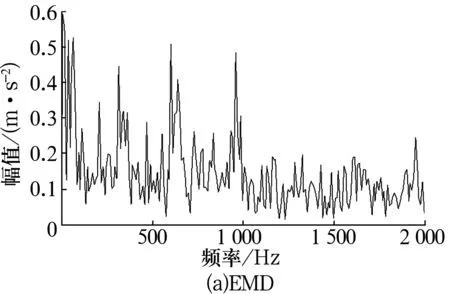
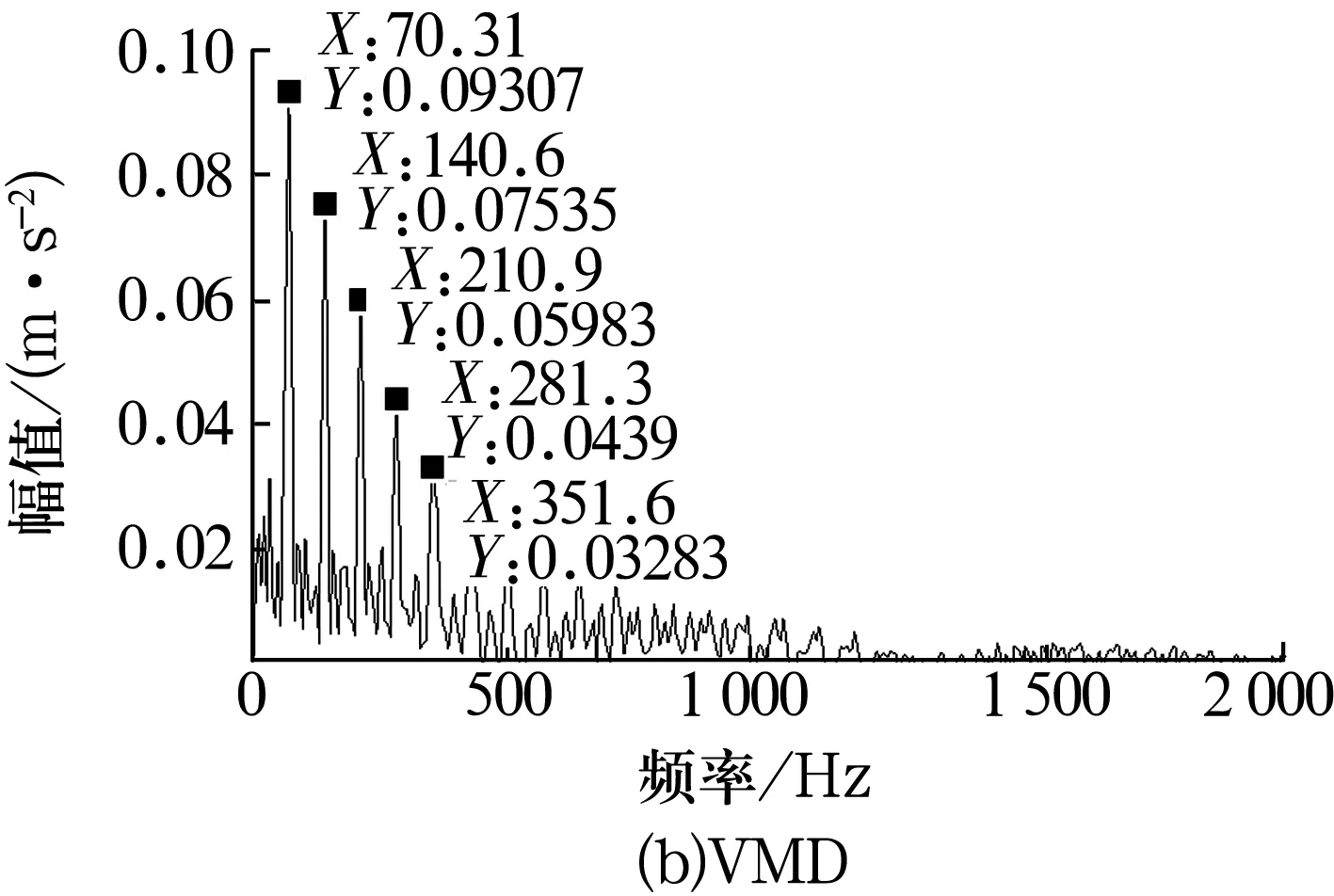
3)令k=0,k=k+1,当k 4)令k=0,k=k+1,当k 。(5) 5)更新λ为 (6) 使用MATLAB2011进行仿真分析,为算法比对的合理性,降低端点效应的影响,在EMD和VMD处理过程中均采用了镜像延拓。VMD算法中的α取默认值2 000;K的取值采用观察中心频率的方法确定[11]。 仿真信号采用多频信号X1(t)和标准差为1的随机噪声信号叠加所得,表达式为 X1(t)=[1+cos(2π×30t)]×cos(2π×125t)+[1+cos(2π×30t)]×cos[2π×155t+cos(2π×5t)]+[1+cos(2π×30t)]×cos(2π×185t)。(7) 采样处理后的仿真信号如图1所示,分别采用EMD(分解过程中采用基于互信息的方法去除了伪分量)和VMD算法进行处理,分解结果如图2所示,分解后IMF的频谱分析结果如图3所示。 图1 仿真信号 图2 不同算法分解后的信号 图3 分解后信号的频谱图 从图3a中可以看出,IMF1中主要包含了155和185 Hz的频率成分;IMF2中主要有125和155 Hz的频率成分;IMF3则混合了65~95 Hz的频率成分。结果表明,对于多分量加噪合成仿真信号,EMD算法的分解效果并不理想,模态混叠严重。这是由于一些微弱的信号和噪声淹没在待分解信号中, EMD在筛分过程中的3次样条包络拟合导致了分解偏差。微弱信号嵌入到强信号的绝大多数地方,EMD均能筛选并提取出,但当微弱信号仅出现在强信号的最大斜率范围上时,微弱信号会以波内频率调制的形式出现,并不产生额外的局部极值点,EMD很难提取,进而产生严重的模态混叠和伪分量。 从图2b和图3b可以看出, VMD不仅能有效去除伪分量,而且每个IMF均表现出某一尺度范围的模态,彼此之间没有模态混叠现象,实现了对仿真信号的多尺度表征,分解效果好于EMD,且具有很好的噪声鲁棒性。 EMD和VMD算法的分解结果都是正交的,即分解后各IMF的能量之和等于分解前信号的能量。但EMD和VMD的分解结果都不同程度地存在端点效应,影响信号的分解精度,导致虚假分量的产生,致使分解后IMF的总能量发生变化。在此,通过分析信号分解前后能量值的变化对比端点效应对EMD和VMD的影响[13]。 求取给定信号X(t)经过EMD和VMD分解后产生的IMF分量的能量 (8) 式中:E为给定信号X(t)或分解后各IMF的能量;x(i)为信号序列;n为信号的采样点数。 比较各IMF能量总和与给定信号能量值之间的偏差,得到评价指标为 (9) 式中:Ex为给定信号的能量;Ep为第p个IMF的能量;K为IMF总数,包括分解的残余项。 由定义可知,ξ越大,分解后的能量泄漏就越大,端点效应越强。ξ=0表示端点效应对分解结果几乎没有影响。构造仿真信号为 X2(t)=sin(2π×3t)+0.3sin(2π×11t)+ 0.8sin(2π×25t)+sin(2π×40t)+0.6cos(2π×100t), (10) X3(t)=[1+0.5cos(2π×4t)]×cos[2π×100t +2cos(2π×5t)]+[1+sin(2π×5t)]×sin[2π× 50t+0.5cos(2π×5t)]。 (11) 分别对3个仿真信号进行分析,采用EMD和VMD处理时不进行镜像延拓,且分解时不去除伪分量,分解后求取的ξ见表1。由表可知,VMD的能量泄漏小,端点效应不明显,结果优于EMD算法。 表1 能量泄漏评价指标 依据实测轴承振动信号,进一步对比分析EMD与VMD算法的分解结果。采用某变速箱轴承内圈故障振动信号,故障轴承型号为KOYO 1205,钢球数Z=12,钢球直径Dw=7.12 mm,接触角α=0,球组节圆直径Dpw=38.5 mm,变速箱运行时轴的转速约为600 r/min(fr=10 Hz),计算得内圈故障特征频率为71.1 Hz。 利用电火花在轴承内圈沟道设置面积约3.58 mm2的点蚀,变速箱装置简图如图4所示,通过B&K3560数据采集仪采样,传感器布置如图5所示,数据长度为65 536,选用变速箱轴承座的垂直振动信号(图5中垂直振动传感器采集的信号)作为故障诊断的研究对象。 图4 变速箱装置简图 图5 传感器布置图 实测振动信号的时域波形如图6所示,从图中可以看出,正常信号波形与内圈故障信号波形类似,很难直接分辨轴承是否存在故障。 图6 实测信号时域波形 截取信号前5 000个采样点的数据作为研究对象。为增强故障脉冲信号,减小噪声干扰,采用基于谱峭度和EMD/VMD的方法进行故障信号的预处理并进行故障诊断的分析对比。 在实测振动信号中,往往包含着故障信号及强烈的加性噪声。由谱峭度的定义[14]可知,在信噪比很高的频率处,谱峭度值大;而在噪声强烈的频率处,谱峭度值趋于0。因此,可以通过谱峭度对IMF进行筛选,寻找出包含故障信号的频带。计算故障信号经EMD或VMD算法分解后各IMF的谱峭度Ki(f),对Ki(f)进行归一化处理,令 (12) 式中:λi为归一化信息值,0≤λi≤1。利用信噪比高谱峭度值大的特点,将λi作为评判故障信号频带存在的指标,并设置故障频带分量的判断阈值为δ,如果λi>δ,则认为该IMF为故障频带分量,否则予以剔除。基于谱峭度和EMD/VMD故障诊断算法流程如图7所示。 图7 基于谱峭度和EMD/VMD的包络谱故障诊断流程图 分别使用EMD和VMD算法对轴承内圈故障信号进行分解,结果如图8所示。从图中可以看出,分解结果非常复杂,很难分辨出具体的故障特征,分别计算各IMF的谱峭度值并归一化处理,结果见表2。 设定阈值δ为0.8,选取EMD算法分解后的IMF2,IMF3和VMD算法分解后的IMF4,IMF5分别进行故障信号重构,并对重构后信号进行包络谱分析,结果如图9所示。 从图9a可以看出,EMD算法分解重构后信号的解调效果欠佳,虽能观察到70 Hz及部分倍频,但轴承内圈故障信号的调制特征没有解调出来,仍存在一定的模态混叠现象。 而从图9b可以看出,经VMD算法分解重构后信号的包络谱中有明显的规律性冲击成分,由于损伤点随内圈转动不断变化,在70.3 Hz及倍频 图8 内圈故障信号的分解结果 表2 各IMF的谱峭度值归一化结果 处(140.6,210.9,281.3 Hz等)有幅值逐渐下降的谱线,并且各倍频处的两边有对称的调制谱线。虽然与理论计算的内圈故障特征频率(71.1 Hz)存在一定差值,但也要考虑钢球在旋转过程中并非是纯滚动,而且轴承存在几何误差和装配误差等因素,因此,可认为VMD算法处理后信号的包络谱图呈现出了典型的轴承内圈故障特征,从而判定轴承存在内圈故障。同理,对轴承外圈及钢球故障进行分析,也取得了很好的效果。 图9 重构信号的包络谱图 VMD和EMD算法均可对信号进行不同尺度的表征,但VMD算法避免了模态混叠以及伪分量的产生,能较好地在不同尺度下表征原信号,且在噪声鲁棒性和避免端点效应方面均优于EMD算法。将VMD和EMD分别与谱峭度相结合,对实测轴承振动信号的故障诊断结果表明,VMD算法的包络谱能更好地反映故障频段的变化及轴承故障的包络谱特征。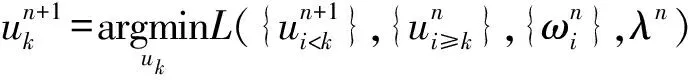
2 仿真分析
2.1 仿真信号的分解对比
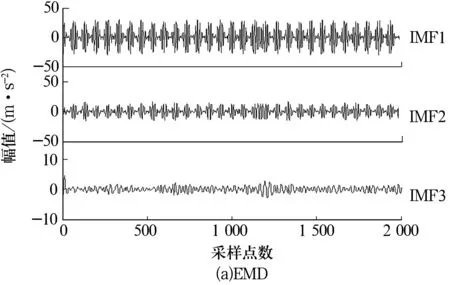
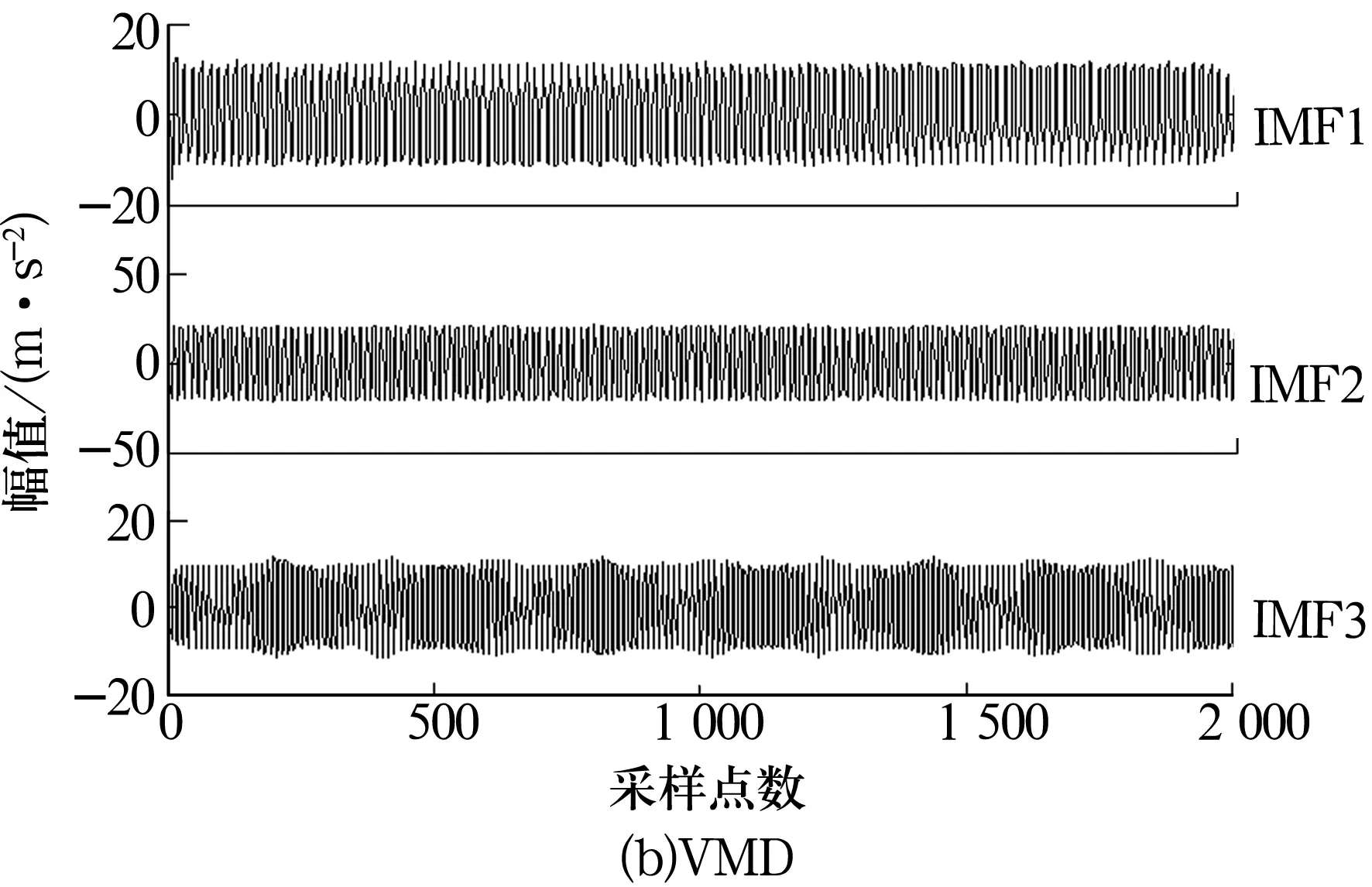


2.2 端点效应的影响
3 基于谱峭度和VMD算法的包络谱故障诊断方法
3.1 试验条件

3.2 诊断流程
3.3 对比分析

4 结束语
