滚动轴承振动性能因素分析的定性融合理论
2016-07-25徐永智夏新涛
徐永智,夏新涛
(1.西北工业大学 机电学院,西安 710072;2. 河南科技大学 机电工程学院,河南 洛阳 471003)
滚动轴承的制造安装因素直接影响其运行过程中的动态特性、使用寿命和可靠性,其中多体现在轴承振动方面,其测量及结果分析受到行业的普遍关注[1];轴承振动信号数据采用时域特征、神经网络法以及光谱分析处理[2-4]来分析轴承故障诊断以及故障处理;文献[5-6]分析了轴承的振动特性及特征参数;文献[7-12]研究了振动与噪声的相关性以及减振降噪的方法措施。以上研究从不同方面揭示了轴承振动的特征,为轴承性能的进一步研究提供了很好的经验,但很少涉及轴承振动影响因素的定性分析。
鉴于此,现提出一种轴承振动性能影响因素分析的乏信息定性融合理论。
1 定性融合理论
定性融合理论:信息系统有很多特征,揭示信息系统特征的方法众多,利用每种方法可揭示信息系统某个侧面的信息特征,从而获得信息系统的特征信息集,对特征信息集进行融合做出合理的决策,最终推断总体特征信息。
1.1 定性融合
定性融合是指在给定的论域U中,已知解集
F=(f1,f2,…,fj,…,fh);j=1,2,…,h,
(1)
fj=(fj1,fj2,…,fjn),
式中:j为方法;h为方法个数。记“属性一致性于”为符号“⊆”,在解集F中,总存在且至少存在一个来自F的元素集合,是满足准则Θ的最终解f0,表示为
f0|Θ|FromF⊆F0,
(2)
式中:F0为系统属性的真值集合即白箱问题;|Θ表示在准则Θ下;|FromF表示来自F的元素。
由于系统信息的复杂多样性,用不同数学方法进行分析会得出不同结果fj,甚至有些结果可能是相互矛盾的。若将这些结果看成是一个个解的集合即解集F,则定性融合是指在某种准则下,从F中提取具有某种一致性元素的子集,并将该子集作为系统的最终解f0。
定性融合有两方面的含义:一是融合,即考虑各个解集;二是定性,即不再进行复杂的数学计算,只是寻求某种一致性,而且最终解中的元素全部来自解集F,没有出现更新的信息。
2 定性融合理论的应用
以圆锥滚子轴承振动加速度为例,基于灰色系统理论[13-14],提出轴承性能影响因素的灰色定性融合分析方法。
影响圆锥滚子轴承振动加速度的因素中,主要考虑套圈和滚子的加工质量参数。加工质量参数很多,必须针对其中的主要因素才能有效地控制轴承振动加速度值。另外,考虑试验成本,生产现场抽样个数较少。在有限的数据个数条件下寻找出最重要的因素是关键问题。
根据轴承乏信息试验分析与评估原理,比较可靠的措施是运用多种数学方法得出多种结论,由于每种结果都有其局限性,因此应对这些结果进行对比分析和融合,得出具有共性的一个结论,该结论就是影响圆锥滚子轴承振动加速度的最重要因素,即问题的最终解。
2.1 轴承性能影响因素分析的定性融合模型
设已知有N个相互独立的因素(如结构参数和润滑条件等)可能会影响轴承的性能(如振动)P,因素符号集为
X=(X1,X2,…,Xi,…,XN);i=1,2,…,N,
(3)
式中:i为影响因素。
用m种数学方法对试验数据进行处理,得到N个影响因素排序集(因素的影响从大到小排序,对性能影响越大的因素,其符号位置越靠左),即对于性能P,有
(4)
可得到排序因素符号矩阵为
(5)
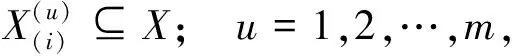
式中:≻表示优于;u为用第u种数学方法。

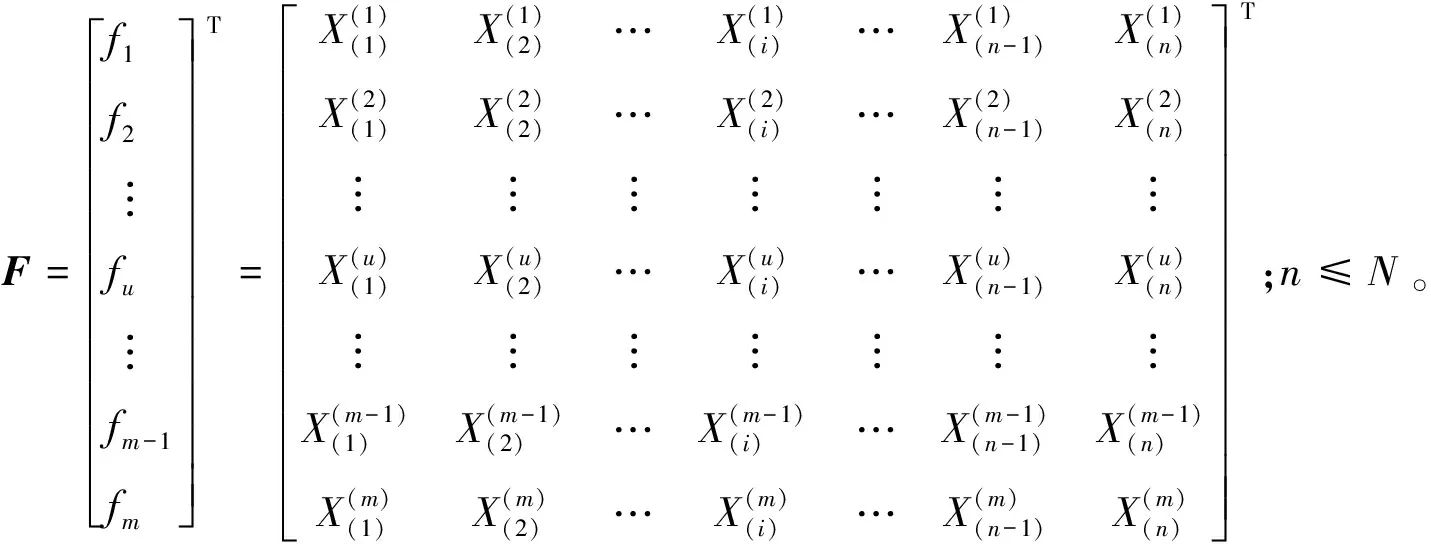
(6)
则最终解f0为F中均具有的因素的集合(符号),即
(7)
若基数f0≠Φ(Φ为非空集合),则定性融合有唯一解。
在最终解f0中,s个因素是不分前后顺序的,均为影响轴承性能P的主要因素,将其改用新的符号并重新编号,有
f0=(x1,x2,…,xi,…,xs)⊂X;1≤s≤n,
(8)
一般n∈[0.5N,N]。由此可以看出在f0中没有新信息。
2.2 解集获取方法
设轴承振动加速度值X0构成的数据序列为
X0=(x0(1),x0(2),…,x0(k),…,x0(K));
k=1,…,2…,K,
(9)
式中:K为数据个数。
影响因素Xi构成的数据序列为
Xi=(xi(1),xi(2),…,xi(k),…,xi(K))。
(10)
2.2.1 灰色关联度方法
1)均值化变换
轴承振动均值化比较数列为
(11)
轴承振动均值化参考数列为
(12)
2)求在各点上X0与Xi的关联系数L0i(k)
(13)
Δ0i=|y0(k)-yi(k)| ,

式中:ξ为分辨系数,ξ∈(0,1)。
3)求关联度
(14)
4)排关联序
将m个子序列对同一母序列的关联度按序排列,组成关联序,其直接反映各个子序列对同一母序列的“优劣”或“主次”关系。若γ0a﹥γ0b,则称子序列Xa对于相同母序列X0有优于子序列Xb的特点。
2.2.2 灰色绝对关联度方法
设序列X0与Xi的长度相同且初值均不为零,则可用灰色绝对关联度来表征X0与Xi的相对始点的几何形状之间的关系,若X0与Xi的几何形状越接近,其绝对关联度越大。灰色绝对关联度计算步骤如下:
1)初值零化处理
轴承振动零值初化的参考数列为
y0(k)=x0(k)-x0(1) ,
(15)
轴承振动零值初化的比较数列为
yi(k)=xi(k)-xi(1) 。
(16)
2)计算绝对关联度
(17)
其中,轴承振动斜率参考数列为
轴承振动斜率比较数列为
灰色绝对关联度ε0i具有以下性质:
1) 0<ε0i≤1;ε0i恒不为零,表明任何2个序列都不是绝对无关的;
2)ε0i只与Xi和X0的几何形状有关,而与其相对位置无关,即平移不会改变绝对关联度的值;
3)ε0i越小,Xi和X0的相似程度越小,联系越不密切;
4)ε0i越大,Xi和X0的相似程度越大,联系越密切;
5)ε0i=1,表明Xi和X0完全相同,无任何区别。
2.2.3 灰色相对关联度方法
1)计算初值像
轴承振动初值像参考数列为
y0(k)=x0(k)/x0(1),
(18)
轴承振动初值像比较数列为
yi(k)=xi(k)/xi(1) 。
(19)
2)求始点零化像
轴承振动零值初化的参考数列为
z0(k)=y0(k)-y0(1),
(20)
轴承振动零值初化的比较数列为
zi(k)=yi(k)-yi(1)。
(21)
3)计算灰色相对关联度
(22)
其中,轴承振动斜率参考数列为
轴承振动斜率比较数列为
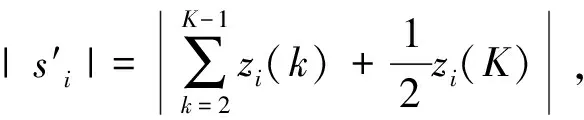
灰色相对关联度γ0i具有以下性质:
1) 0<γ0i≤1;γ0i恒不为零,表明任何2个序列都不是绝对无关的;
2)γ0i可以表示Xi和X0相对初始点的变化速率之间的关系,Xi和X0的变化速率越接近,γ0i就越大,反之就越小;
3)γ0i=1,表明Xi和X0完全相同,无任何区别。
2.3 应用实例
以30204型圆锥滚子轴承的振动加速度问题为例,通过试验来研究轴承套圈和滚子的参数与轴承振动之间的关系,以寻求控制轴承振动质量的乏信息方法。
以30204轴承的16个套圈参数和16个滚子参数作为研究对象。质量参数共32个,其中宏观误差参数21个,微观误差参数7个,其他4个;滚子质量参数16个,内圈质量参数9个,外圈质量参数7个,通过试验研究轴承各项参数与振动之间的关系。
试验所用符号及其含义见表1。其中,“均”代表一套轴承中15个滚子该项参数的均值;“差”代表一套轴承中15个滚子该项参数的极差。

表1 滚动轴承符号
轴承振动加速度X0的测量结果为
46.0,47.7,47.7, 47.0,48.0,47.7,48.0,47.7,47.7,46.7,47.7 ,44.0,46.0,46.7,48.0,45.0,47.0,45.3,45.7,45.3,47.3,48.0 ,47.0,47.3 ,47.3,47.0,47.3,46.7,44.6,47.3 dB。参数X1~X32的试验数据见表2~表5。

表2 滚子测量数据(均)

续表 μm

表4 内圈测量数据
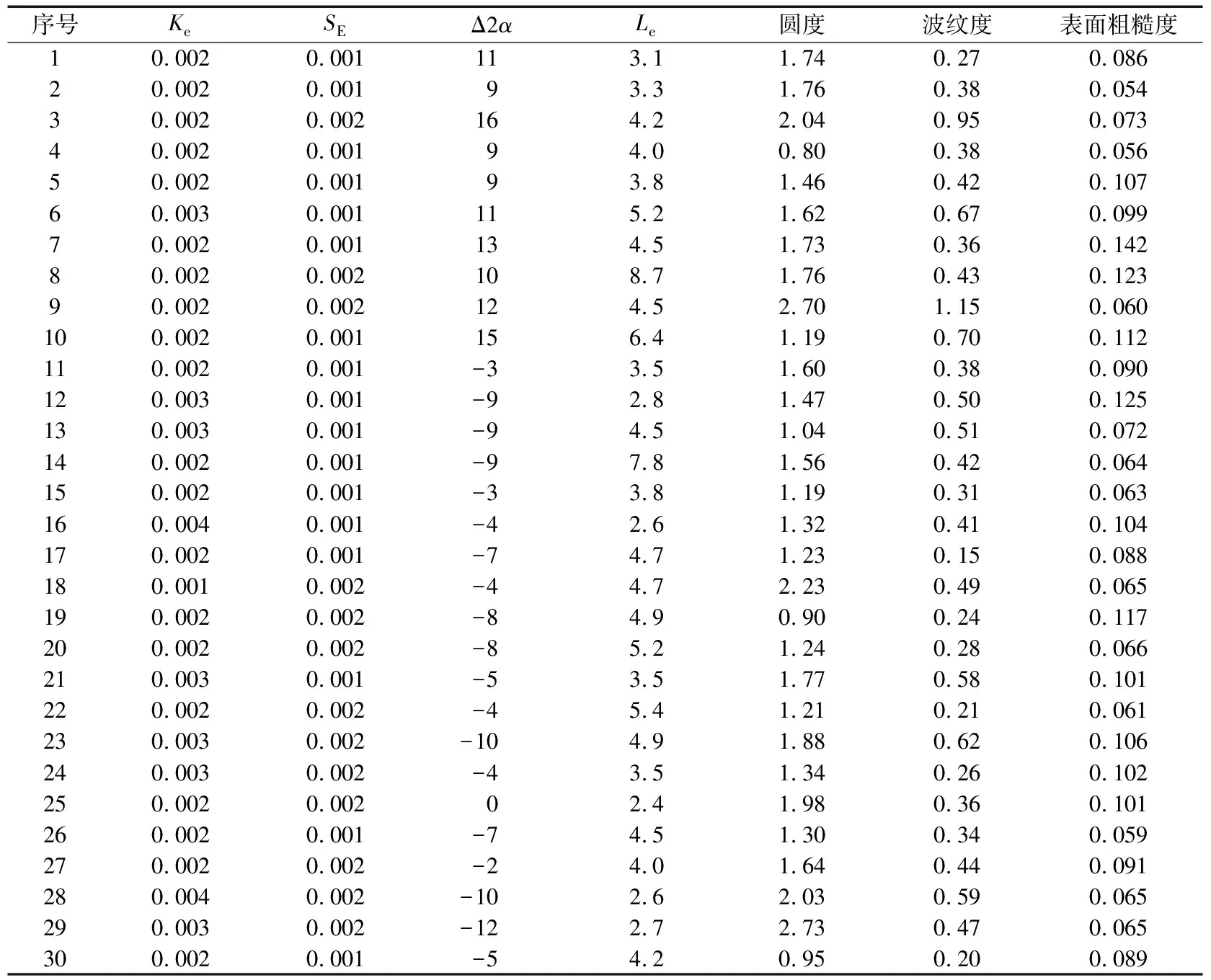
表5 外圈测量数据
根据灰色关联度法(ξ=0.5)、灰色绝对关联度法、灰色相对关联度法,得到各参数与振动的关联度、绝对关联度、相对关联度,结果见表6(按照从小到大的顺序排列)。
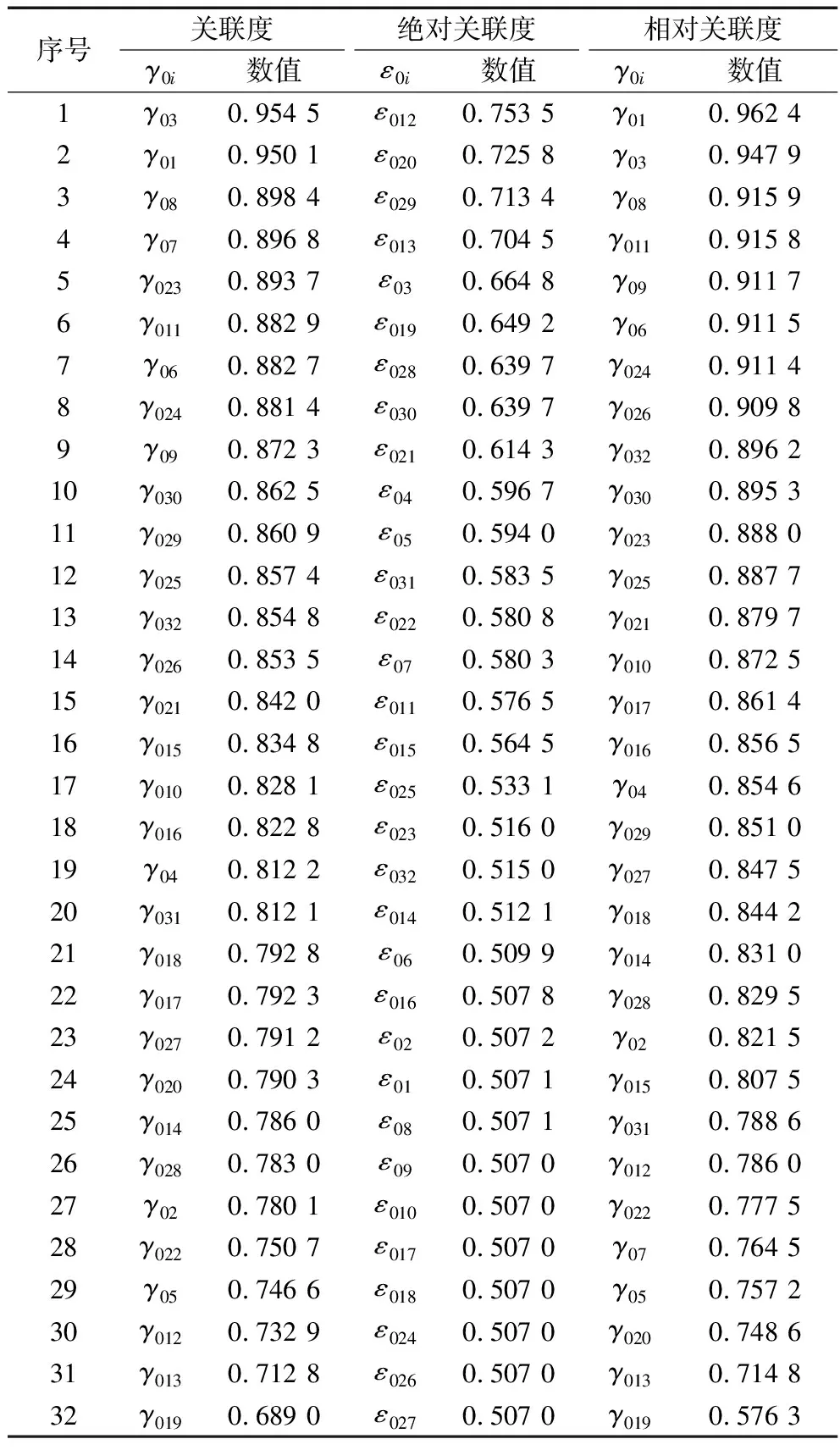
表6 轴承参数与振动的关联度
将以上3种方法排序结果中前16名取出,用因素符号Xi列于表7。由表可知,最重要的因素集合为f0=(X3,X11,X21,X30)。

表7 3种方法计算结果的前16名因素
在3种数学方法的排序结果中,将前16名因素作为可能的重要因素,其出现的频数和影响程度分别见表8、表9,将表8中的影响因素进行分类,结果见表10。

表8 影响因素在3种计算结果中出现的频数

表9 3种方法中各因素的影响程度

表10 主要影响因素的误差类型
由表9、表10可知,共有28个主要因素,其中滚子质量参数14个,内圈质量参数8个,外圈质量参数6个。因此,试验轴承零件对振动加速度的影响权重比为滚子/内圈/外圈=14/8/6≈2.3/1.3/1。
从最重要因素和第2重要因素中发现,共有16个主要因素,其中滚子质量参数8个,内圈质量参数4个,外圈质量参数4个。因此,试验轴承零件对振动加速度的影响权重比为滚子/内圈/外圈=8//4/4=2/1/1。
从最重要因素中发现,共有4个主要因素,其中滚子质量参数2个,内圈质量参数1个,外圈质量参数1个。因此,试验轴承零件对振动加速度的影响权重比为滚子/内圈/外圈=2/1/1。
综上所述,在测量条件下,对试验轴承振动加速度贡献最大的是滚子,其次是内圈和外圈。主要原因是滚子质量参数最多,内圈次之,外圈最少。
试验发现,对滚子而言,圆锥表面素线凸度是试验轴承的最薄弱环节。说明凸度的形状、大小及加工质量对轴承振动加速度有重要影响;对套圈而言,滚道圆度误差是试验轴承的最薄弱环节。以上4个质量参数均为宏观误差参数。
理论上,在使用过程中,圆锥滚子轴承滚子的2条素线、中心线以及轴承中心线相交于一点时,轴承的振动最小;然而,在轴承设计时应考虑应用载荷的影响。当应用载荷等于设计载荷时,滚子的2条素线、中心线以及轴承中心线相交于一点,轴承振动较小;但实际应用中应用载荷和设计载荷并不相等,滚子凸度受载时,滚子的2条素线、中心线以及轴承中心线并不相交于一点,滚子与套圈接触的直线长度发生变化而产生振动,可见,滚子凸度影响轴承的振动。应用载荷和设计载荷相差越大,其影响程度就越大;而同类因素的直线度则受载荷影响较小,对振动影响较小。本试验中试验载荷和设计载荷不相等,滚子凸度是影响轴承振动的最大因素,因此与波纹度、圆度、表面粗糙度是最大影响因素的结论有所出入。
3 结束语
定性融合性分析方法是轴承及其他机械产品性能研究的发展方向。其意义在于:一是从经济学角度,能够从少量试验中得到大量信息,做出合理的评估、预测,可以大大降低成本;二是从信息量的角度,能够利用一些数学工具及理论融合,在相同试验数据中挖掘出大量信息,大大提高资源的利用效率。
融合性分析方法也有缺点和许多需要完善之处,如融合性分析方法的范围,上述只是其中一部分方法的融合,还有许多其他方法有待挖掘、完善;融合性分析方法对适用对象有要求,要根据其特点选择不同方法融合;在融合性分析方法使用过程中参数的确定也有待进一步研究。
