无铅焊料中孔洞率的反演辨识

朱玲玲，郭源齐，许杨剑，刘 勇，梁利华

（浙江工业大学 机械工程学院，浙江 杭州 310014）



可 靠 性

无铅焊料中孔洞率的反演辨识

朱玲玲，郭源齐，许杨剑，刘 勇，梁利华

（浙江工业大学 机械工程学院，浙江 杭州 310014）

摘要:为了确定无铅焊料中的孔洞含量，提出了一种单轴拉伸实验与卡尔曼滤波算法(KF)相结合的反演分析方法。该方法以单轴拉伸实验中获得的载荷-位移曲线为依据，结合有限元仿真，对焊层中的孔洞率进行反演辨识。反演结果表明：基于伪实验数据的孔洞率反演，所得到的最大误差保持在2%以下；针对真实试样的孔洞率反演，最大误差保持在3%左右。由此证明该方法在无铅焊料孔洞率的反演分析上是行之有效的。

关键词:无铅焊料；孔洞；内聚力模型；反演分析；卡尔曼滤波算法；金属间化合物

朱玲玲（1991―），女，浙江温州人，研究生，研究方向为微电子封装技术，E-mail:zhulingling317@126.com 。

网络出版时间：2016-05-31 11:09:43 网络出版地址：http://www.cnki.net/kcms/detail/51.1241.TN.20160531.1109.020.html

随着电子制造业向高密度、小型化、薄型化发展，电子产品中的无铅焊料必须具备较高的可靠性[1]。但在加工过程中常有不可避免的孔洞存在于焊点，这些孔洞常常充当了裂纹尖端从而加速了焊接界面的失效[2-4]。孔洞的特性表征主要有孔洞率、孔洞分布以及孔洞大小的配比，而孔洞率是对焊点性能影响最大的一个特性。为此，获得焊点内部的孔洞率对于焊点的可靠性研究具有重要的意义。目前，用于探测焊点内部孔洞率的方法有许多，包括X射线衍射法、超声波衰减法以及同步辐射法等[5-6]。这些方法虽然能够获得较高的孔洞率探测精度，但是对实验设备有较高的要求。因此，一些对实验设备要求不高的孔洞率识别方法被提出，如反演分析法。针对该方法的研究是当前学术界的一个热门方向，在许多行业中都能见其身影。

反演分析法最初用于地球物理学，其原理是通过分析地震波信息来反演地球内部构造。近几十年反演分析法也被广泛地研究并且运用到热传导以及固体力学中[7-8]。虽然反演分析方法被广泛运用于材料力学，但目前却较少有学者将反演分析方法运用于材料内部孔洞含量的预测。此外，反演方法也是多种多样，但是大都有一定的适用性及弊端。如反演误差较大和反演效率低等。要开展正确的反演分析，其首要条件是，能够找到合理描述物理现象的理论模型。本文为此提出了一种改进的内聚力模型（CZM），能够合理地描述考虑孔洞的情况下金属间界面化合物及焊锡合金的失效行为。为正确的反演分析奠定了基础。此外，笔者采用稳定性较好的卡尔曼滤波算法(KF)[9-10]，结合响应面方法来开展反演分析[11]。为快速实现参数的反演辨识提供了保障。

本文的侧重点主要是集中在失效表征和反演方法的研究上。因此没有选择结构复杂、影响因素较多的实际微小焊球，而是选择焊层中含有贯穿型孔洞的铜/焊锡粘接试样作为孔洞率反演辨识的研究对象。该方法能够为带有孔洞的焊锡材料的力学性能表征提供一个新的思路。

1　 反演分析方法

反演分析方法的本质是由结果或者与结果相关的信息反推出事件发生的原因或者机制。无铅焊料中贯穿型孔洞的孔洞率与界面的粘结性能密切相关，因此采用单轴拉伸实验获取载荷-位移曲线用作反演分析。

反演分析采用的卡尔曼滤波迭代算法可将非线性问题转化成线性问题，并且具有收敛效率高、适定性强等优点。KF在利用单轴拉伸实验进行无铅焊料孔洞率的反演分析中依赖于三个重要的参数：当前状态测量值、上一状态估计值以及决定当前状态进度的梯度信息，即实验或模拟获得的载荷-位移曲线、反演算法迭代后获得的参数解对应的曲线数据以及其相应的梯度信息[12]。KF的迭代方程表达式通常表达为：

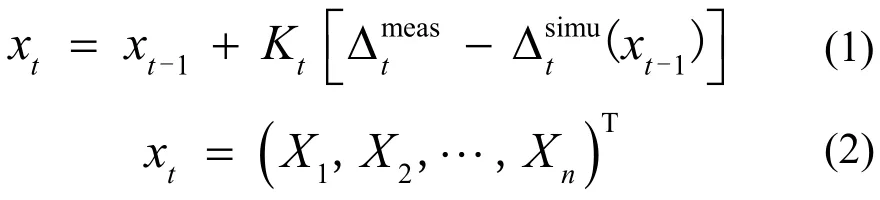
式中：xt是包含n个未知材料参数的当前状态量，其下标表示离散化处理后的当前载荷步；是当前载荷步下实验或模拟获得的位移向量；是根据上一载荷步估算参数xt-1得到的位移向量；Kt是卡尔曼滤波增益矩阵。增益矩阵Kt可表示成：

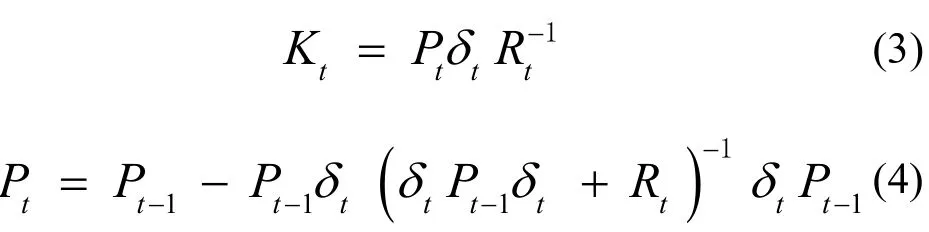
式中：Rt和Pt分别是误差协方差矩阵和测量协方差矩阵；为梯度矩阵，决定了KF的迭代更新方向，即决定当前状态进度的梯度信息，可表示为：

此外，为使卡尔曼滤波算法获得稳定解，有效地降低噪声，需排除实验中由于种种不可控因素而导致的随机误差。本文对通过实验或模拟获得的位移值进行逐步均匀化处理，以提高参数解的精度和稳定性[13]。逐步均匀化修正公式可表示为：

2　 改进内聚力模型

本文采用有限元数值模拟的方法获取反演信息库。为了获得可靠的载荷-位移曲线，保证反演信息库的适用性，必须考虑裂纹扩展以及断裂的问题。目前研究裂纹扩展的方法有J积分法、面积能量释放率法、内聚力模型法等。其中，内聚力模型法不但简单、有效，还可以同时用于分析韧性材料和脆性材料的断裂破坏[14]。由于无铅焊料本身是韧性材料且熔点较高，与铜反应时会产生多层脆性合金，因此选择内聚力模型研究含孔洞界面的粘接性能。

由Tvergaard等[15]提出的三线性内聚力模型是较为流行的模型之一，该模型不但计算简单、结果精确，并能在一定程度上模拟材料的延性。但是，三线性内聚力模型不能表征多数材料在延性阶段应力仍会有弱于弹性阶段的小幅增长。为此，本文对三线性内聚力模型提出改进，以描述无铅焊料在延性阶段应力的小幅增长；同时，由于无铅焊料切向延性较差，因此采用双线型张力位移关系作为切向内聚力模型[16]。最后，通过ABAQUS的VUEL接口实现其运用。本文改进的内聚力本构模型如图1所示。

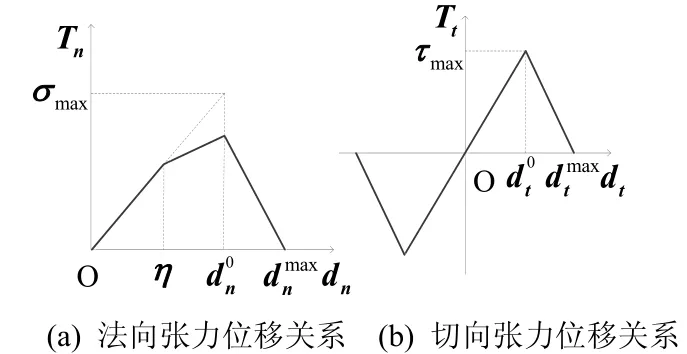
图1 改进的内聚力本构模型Fig.1 Improved CZM constitutive model

其控制方程为：

式中：Tn为法向张力；tT为切向张力；而dn为法向位移；dt为切向位移；σmax与tmax分别为法向及切向能达到的最大张力，而此时的界面张开位移分别对应

3　 单轴拉伸实验及有限元模拟

3.1 单轴拉伸实验

为了验证上述单轴拉伸实验与卡尔曼滤波迭代算法相结合的反演分析方法的准确性与适用性，首先对孔洞率为0的铜/焊锡粘接试样进行分析，以确定界面内聚力参数。铜/焊锡粘接试样如图2所示，其中无铅焊料采用Sn-3.0Ag-0.5Cu(SAC305)，尺寸为相应的焊接件是电子制造业常用的紫铜，尺寸为，其中圆柱部分长为20mm。铜棒表面进行打磨抛光后，采用丙酮溶液清洗试样表面，以抑制焊层界面中孔洞的产生，随后用熔焊的方法得到Cu/SAC305焊层。

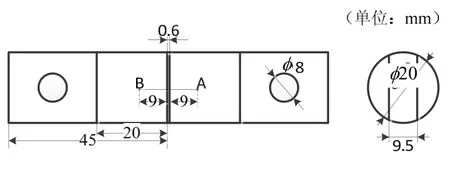
图2 铜/焊锡粘接试样示意图Fig.2 Schematic drawing of copper/solder specimen

铜-焊锡粘接试样的拉伸曲线受很多因素的影响，包括焊层中的孔洞率、焊锡层的厚度、焊锡材料保持熔融状态的时间以及实验的拉伸速率。本文只需要考虑孔洞率对拉伸性能的影响，因此将试样的焊层厚度控制为0.6mm，熔融时间定为2 min，拉伸实验机的拉伸速率设置为0.2mm/min。

铜/焊锡粘接试样的单轴拉伸实验在INSTRON8801台式万能拉伸机上进行，载荷由DYNACE II传感器记录。在试样两端距离Cu/SAC305界面9mm处分别设置一个观测点(即图2中的A、B两点)，将两点之间的分开位移作为铜/焊锡拉伸曲线中的位移参数。观测点之间的相对位移由非接触全场的位移测量系统(VIC-3D)来测量。由于该系统的工作原理基于数字散斑技术，因此需要在试样表面喷涂散斑如图3所示。

图3 铜/焊锡粘接试样Fig.3 Copper/solder specimen

铜/焊锡粘接试样断裂结果表明Cu/SAC305界面处有三种断裂形式：一种是破坏全部发生在界面金属间化合物(IMC)内的脆性断裂；另一种是破坏全部在焊锡合金内部的韧性断裂；还有一种是包含了这两种破坏形式的混合式断裂。根据拉伸试样断层形貌（图4）可知，实验的主要断裂形式是从一个界面的IMC层过渡到另一个界面的IMC层的混合式断裂。

图4 试件断口形态Fig.4 Macroscopic fracture appearances of specimens

3.2 有限元模拟

根据圣维南原理，有限元分析中取铜棒长度为9mm，对铜/焊锡粘接试样进行简化建模，模型示意图及网格划分情况如图5所示。其中，铜棒的网格

图5 铜/焊锡粘接试样的有限元模型Fig.5 FE model of copper/solder specimen

表1 材料参数Tab.1 Material properties

I型断裂模式下，内聚力参数可由单轴拉伸实验获得。由于试样制备过程的人工误差与实验过程中的测量误差，铜/焊锡粘接试样的拉伸曲线并不完全一致。将实验数据中集中性较好的几组的均值作为内聚力模型的参数依据。所得的内聚力参数见表2。

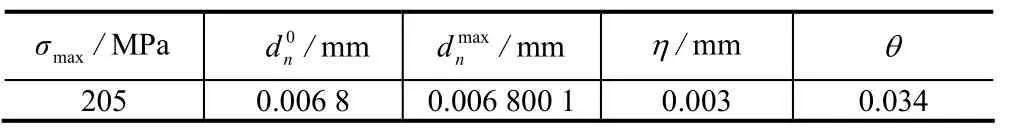
表2 内聚力参数Tab.2 Parameters of cohesive zone model

该组内聚力参数的仿真结果与实验比较如图6所示，仿真曲线与实验数据的吻合效果较好。可见，改进内聚力模型结合表2的参数可以较好地表征Cu/SAC305之间的粘结性能。

图6 无孔试样仿真曲线与实验曲线的比较Fig.6 Comparison between numerical and experimental results of specimen with no void

4　 无铅焊料中孔洞率的反演辨识

4.1 孔洞率反演分析方法的实现

利用卡尔曼滤波迭代算法做反演分析时，需计算大量的载荷-位移值以及相应的梯度信息。为了提高反演分析的效率，取4种不同孔洞率模型的载荷-位移曲线作为反演信息库，并以此构造载荷-孔洞率响应，然后对其进行插值，以减少有限元计算的次数。载荷-孔洞率响应构造步骤：1) 假设孔洞率P的参数范围，5%≤P≤20%；2) 根据拉格朗日插值函数的要求确定插值的基准点。本文采用三次插值函数对孔洞率的参数范围进行插值，因此需要对孔洞率的参数范围进行三等分，即共有4个基准点。3) 针对基准点对应的孔洞率(5%，10%，15%，20%)进行有限元计算，得到不同载荷步下的载荷-孔洞率响应值；4) 基于上述基点计算结果，通过拉格朗日插值函数得到每个载荷步下的孔洞率响应值，即一个载荷步对应一组载荷-孔洞率响应；5) 通过载荷-孔洞率响应即可插值获得任意载荷值对应的孔洞率。例如，图7表示4组孔洞率对应的载荷-位移曲线。A点的载荷值结合载荷步t=15所对应的载荷-孔洞率响应，根据拉格朗日插值函数就可得出A点所对应的孔洞率。

图7 载荷与孔洞率之间的响应关系Fig.7 Response relationship between load and void volume fraction

通过上述反演信息库的运用发现，反演信息库的准确性影响着孔洞率的反演结果。但是，孔洞率反演信息库在一定程度上会受孔洞存在的其他特性如孔洞分布与孔洞大小配比的干扰。因此，针对基点对应的4个孔洞率(5%，10%，15%和20%)，在每一个孔洞率下都设置12组孔洞分布随机的模型。同时，将这12组模型分别按小孔占主导、大小孔均匀、大孔占主导的配置各建立4组。将这些模型结合表2中的内聚力参数，获得含孔洞的铜/焊锡粘接试样的拉伸曲线。利用公式(6)对同一孔洞率下的12组拉伸数据进行均匀化处理，最终得到该孔洞率下的载荷-位移曲线，并以此构造反演信息库进行反演计算。

本文利用FORTRAN实现上述孔洞模型，首先根据需要确定有孔洞的截面尺寸，指定所需的孔洞率；然后设置不同孔洞尺寸的配比；最后运用函数生成分布随机的2D圆形孔。为确保所得孔洞率的准确性，必须排除孔与孔相交、重叠的可能性。当新产生的圆形孔与之前产生的圆形孔相交或重叠时，则将新产生的圆形孔删除，具体流程如图8所示。4种孔洞率下的代表性分布如图9所示。

图8 随机孔洞模型建模流程图Fig.8 Flow chart of random void modeling

图9 孔洞代表性分布Fig.9 Representive distribution of voids

本文采用单轴拉伸实验结合卡尔曼滤波算法的反演分析流程如图10所示。首先通过无孔试样的单轴拉伸实验得到内聚力参数，用于描述铜/焊锡界面的粘结性能；然后结合内聚力参数对4个基准点对应的孔洞率试样进行有限元仿真得到载荷-位移曲线，并以此作为反演信息库。再将有孔试样单轴拉伸实验得到的载荷-位移曲线与非基准点对应的孔洞率试样有限元仿真获得的载荷-位移曲线作为反演目标。最后，根据反演信息库构建载荷-孔洞率响应，利用卡尔曼滤波算法对反演目标数据进行逐步迭代更新，直至获取反演结果。

图10 结合单轴拉伸实验与卡尔曼滤波迭代算法的反演分析流程Fig.10 Flow chart of the inverse analysis combining uniaxial tension test and the KF algorithm

4.2 反演实例

本文分别建立了一组伪实验与四组真实验，验证孔洞率反演辨识方法的可靠性与适用性。在铜/焊锡粘接试样有限元模型的焊层中加入8%的孔洞率进行有限元分析(图11)，值得一提的是此时的内聚力单元只存在铜/焊锡之间，不包含孔洞部分。将得到的载荷-位移曲线作为伪实验的数据组，对数据分别添加1%，5%，10%和15%的噪声，以其作为反演目标。图12为考虑不同噪声的8%孔洞率模型的拉伸数据。

表3表明，每组反演目标均能收敛获得反演结果，且最大误差只有1.68%，这证明卡尔曼滤波算法具有较强的抗噪声能力。利用卡尔曼滤波算法对无铅焊料进行孔洞率反演分析，得到的反演结果收敛性好、精度高。

图11 含8%孔洞率的铜/焊锡粘接试样有限元模型Fig.11 FE model of copper/solder specimen with 8% void volume fraction

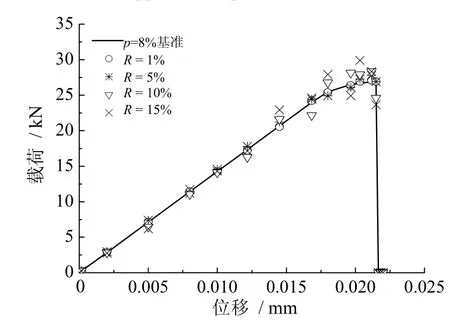
图12 考虑不同噪声的8%孔洞率模型的载荷-位移曲线Fig.12 Load-displacement curves of 8% void rate with different noises

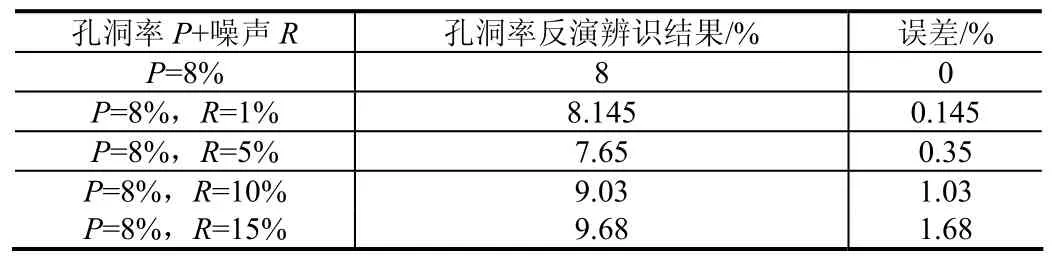
表3 考虑不同噪声的8%孔洞率模型的反演结果Tab.3 Inverse results of 8% void rate model with different noises

为进一步验证孔洞率反演法的适用性，制作焊层中有贯穿型孔洞的铜/焊锡粘接试样。进行单轴拉伸实验后，将载荷-位移曲线作为反演目标进行反演分析。采用液态光致阻焊剂(绿油)阻止铜与焊锡之间的反应，以达到制造贯穿型孔洞的效果。利用图像法处理分别得到4个试样的孔洞率用于反演结果的对比，其断口形貌如图13所示。

图13 含孔洞试样的断口形态Fig.13 Macroscopic fracture appearances of specimens with voids

在孔洞的形貌中，除阻焊剂制造出的大且形状复杂的贯穿型孔洞外，界面上还存在一些微小的孔洞。相较于大孔洞、贯穿型孔洞，小孔洞、界面孔洞对于试样的拉伸性能影响较小，因此这里只考虑直径大于0.1mm的贯穿型孔洞。以上4个试样的断裂形式有IMC断裂(a)和混合断裂(b)、(c)、(d)(图14)，因此其载荷-位移曲线的形状也不相同。对无铅焊料中的孔洞率进行反演分析，需要根据反演目标的断裂形式选择对应的反演信息库。改进内聚力模型，可以很好地模拟不同断裂形式下的载荷-位移曲线(图14)，用以建立相关反演信息库。

图14 含孔洞试样实验曲线与模拟曲线的比较Fig.14 Comparison between the experimental and numerical curves of specimen with voids

各试样的孔洞率反演结果如表4所示。反演结果误差最大的是试样A，偏差为3.03%。由此说明，本文的孔洞率反演分析法具备较高的精确度和可靠性。反演结果的误差可能由二个原因引起：一是试样断裂形式不同。IMC断裂形式下，粘接试样的拉伸曲线之间刚度区别较小，因而导致该反演结果的误差在4个试样中最大；二是用图像法获取的孔洞率，因其未考虑界面细小的孔洞，导致反演结果偏大。

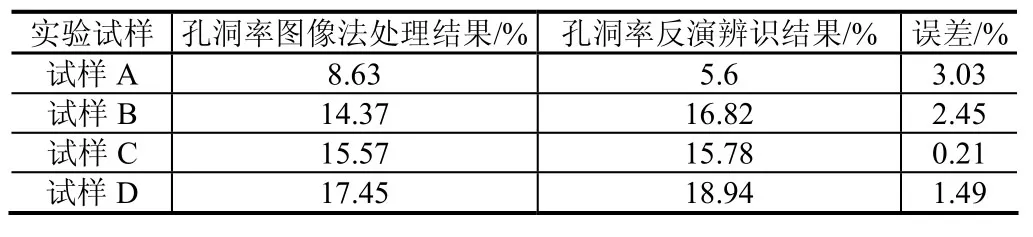
表4 含孔洞试样的孔洞率反演结果Tab.4 Inverse results of specimen with voids

5　 结论

提出了一种单轴拉伸实验与卡尔曼滤波迭代算法相结合的反演分析法用于无铅焊料中孔洞率的辨识。并且采用改进内聚力模型模拟铜/焊锡界面的粘结性能。通过单轴拉伸实验，确定了改进内聚力模型的相关参数，结合有限元模型建立反演信息库。一组伪实验和四组真实验的反演结果表明，本文所提出的单轴拉伸实验与卡尔曼滤波迭代算法相结合的反演分析法对孔洞率反演辨识误差较小，抗噪声能力较强，具备较高的可靠性与准确性。本文立足于方法的研究，因此选择载荷-位移响应曲线作为反演分析的依据。目前这一方法能为实现无铅焊料孔洞率的预测和失效模拟提供一个思路，但是在芯片封装的实际应用中需要选择其他信息（如电阻率的变化等）开展反演分析。

参考文献：

[1] 李继超, 黄福祥, 杜长华, 等. Sn-Zn-Cu-Al 无铅钎料的组织及性能分析 [J]. 重庆理工大学学报(自然科学版), 2012, 26(2):64-70.

[2] OTIABA K C, OKEREKE M I, BHATTI R S. Numerical assessment of effect of void morphology on thermo-mechanical performance of solder thermal interface material [J]. Appl Therm Eng, 2014, 64(1):51-63.

[3] 甘卫平, 张海旺, 刘妍, 等. 低温烧结型银基浆料烧结膜孔洞率的研究 [J]. 电子元件与材料, 2008, 27(6):18-21.

[4] YU Q, SHIBUTANI T, KIM D, et al. Effect of process-induced voids on isothermal fatigue resistance of CSP lead-free solder joints [J]. Microelectron Reliab, 2008, 48(3):431-437.

[5] PENG S H, NAM H D. Void defect detection in ball grid array X-ray images using a new blob filter [J]. J Zhejiang Univ Sci C, 2012, 13(11):840-849.

[6] LIU J, SHI T, WANG K, et al. Defect detection of flip-chip solder joints using modal analysis [J]. Microelectron Reliab, 2012, 52(12):3002-3010.

[7] KONTOGIANNI V A, STIROS S C. Predictions and observations of convergence in shallow tunnels:case histories in Greece [J]. Eng Geol, 2002, 63(3):333-345.

[8] ELKUT F, BRADLEY G R, KRYWONOS J, et al. Numerical study of the mechanics of indentation bending tests of thin membranes and inverse materials parameters prediction [J]. Comput Mater Sci, 2012, 52(1):123-127.

[9] NAKAMURA T, WANGA T, SAMPAH S. Determination of properties of graded materials by inverse analysis and instrumented indentation [J]. Acta Mater, 2000, 48(17):4293-4306.

[10] VASILEIOS K, CHRISTOPHOROS N, ARISTIDIS L. Visual tracking using the earth mover's distance between Gaussian mixtures and Kalman filtering [J]. Image Vision Comput, 2011, 29(5):295-305.

[11] XU Y J, LI X Y, WANG X G, et al. Inverse parameter identification of cohesive zone model for simulating mixed-mode crack propagation [J]. Int J Solids Struct, 2014, 51(13):2400-2410.

[12] 李翔宇, 许杨剑, 王效贵, 等. 基于卡尔曼滤波算法的功能梯度材料参数辨识 [J]. 工程力学, 2013, 30(11):251-259.

[13] 许杨剑, 李翔宇, 王效贵. 基于遗传算法的功能梯度材料参数的反演分析 [J]. 复合材料学报, 2013, 30(4):170-176.

[14] 钟礼君, 杨道国, 蔡苗. 叠层QFN器件界面层裂失效研究 [J]. 电子元件与材料, 2009, 28(10):57-61.

[15] TVERGAARD V, HUTCHINSON J W. The relation between crack growth resistance and fracture process parameters in elastic-plastic solids [J]. J Mech Phys Solids, 1992, 40(6):1377-1397.

[16] BARENBLATT G I. Equilibrium cracks formed on a brittle fracture [J]. Dokl Akad Nauk SSSR, 1959, 127(1):47-50.

（编辑：陈渝生）

Inverse determination of void volume fraction in lead-free solder

ZHU Lingling, GUO Yuanqi, XU Yangjian, LIU Yong, LIANG Lihua
(College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:To determine the void volume fraction of lead-free solder, an inverse analysis method based on an uniaxial tensile test with Kalman filter (KF) algorithm was proposed. In this method, the load-displacement curves from uniaxial tensile test were used in combination with finite element simulation to determine the void volume fraction inverse analysis of solder layer. Inverse analysis result shows that the error based on pseudo-experimental data is below 2% and the error from real experimental specimen is lower than 3%. It indicates that the present inverse analysis method is effective and its result is reasonable.

Key words:lead-free solder; void; cohesive zone model; inverse analysis; Kalman filter algorithm; IMC

doi:10.14106/j.cnki.1001-2028.2016.06.020

中图分类号:TG42；O302

文献标识码:A

文章编号:1001-2028（2016）06-0092-06

收稿日期：2016-03-23 通讯作者：许杨剑

基金项目：国家自然科学基金资助项目（No. 51375448; No. 51375447）

作者简介：许杨剑（1979－），男，浙江东阳人，副教授，博士，从事固体力学、微电子封装技术研究，E-mail:xuyangjian571@163.com ；