振动载荷下特种设备中电路板级焊点疲劳寿命预测
2016-07-23谢小娟
谢 小 娟
(广东省特种设备检测研究院 珠海检测院,广东 珠海 519000)
振动载荷下特种设备中电路板级焊点疲劳寿命预测
谢 小 娟
(广东省特种设备检测研究院 珠海检测院,广东 珠海 519000)
摘要:基于内聚力模型,提出一种用于振动载荷下特种设备中电路板级焊点疲劳寿命预测的介观尺度模型。将单调载荷与振动周期载荷相结合,建立焊点累积损伤参数来表征焊点的剩余疲劳寿命,利用焊点损伤累积率来表征焊点损伤演化规律。以Sn3.0Ag0.5Cu(SAC305)细间距无铅焊点为例分析了模型参数确定方法,并通过振幅为5mm 与10mm的定频振动试验对模型的预测精度进行了验证,寿命预测结果误差小于10%。由于模型参数为焊点钎料累积塑性应变的固有函数,与焊点尺寸与几何形态无关,通过小样本试验,数据一经确定即可应用于同种钎料不同尺寸焊点在不同振动等级下的疲劳寿命预测,节约了时间与试验成本,该模型能为特种设备中的电子组件提供一种评估板级焊点疲劳寿命的简洁、实用方法。
关键词:振动载荷;内聚力模型;累积损伤参数;板级焊点;累积塑性应变;寿命预测
网络出版时间:2016-05-31 11:11:57 网络出版地址:http://www.cnki.net/kcms/detail/51.1241.TN.20160531.1111.021.html
近年来特种设备中的电子组件越来越多,例如控制电梯轿厢升降的电路组件,控制锅炉启停和安全连锁装置工作的电路组件等。这些都直接关乎特种设备的安全运行,然而由于特种设备的服役环境越来越严酷,电子设备故障引发的电梯坠落、锅炉泄漏等特种设备事故频发,甚至造成不必要的人员伤亡,特种设备中的电子组件可靠性逐渐成为研究的焦点。
在电梯和锅炉的服役过程中,其电子组件经常处于随机振动与冲击的环境中。在振动冲击载荷下,电子组件基板或者印刷电路板(PCB)会产生较大的弯曲变形,使焊点在交变应力作用下疲劳失效,进而导致电子设备故障或失效。一直以来,对焊点的热疲劳研究较多,而对焊点的振动疲劳研究较少。随着电子产品的无铅化,大量试验数据表明,相比于传统Sn-Pb焊点,无铅焊点的硬度和脆性都较大,其对振动载荷更加敏感[1-3]。因此研究振动载荷下无铅焊点的可靠性具有重要意义。
目前,关于焊点振动可靠性研究主要有两大类方法。一类是经验公式法[4-7]。基于试验数据建立焊点寿命与被测物理量(如非弹性应变范围)的函数关系。由于这种经验方法没有阐明引起疲劳失效的损伤机理,当外加负载超出试验范围时,公式就不再具备预测疲劳失效能力。另一类方法是机械方法[8-12]。基于连续介质损伤力学建立体现焊点本构行为的细观力学模型,为保证模型的预测精度需要用大量的材料参数去表征焊点的损伤行为与规律,而这些材料参数需要设计试验和测量方法通过试验获取,即使借助于有限元方法,工作量依然巨大。上述的这两类方法都无法满足电子产品设计初期对焊点寿命进行评估的需要。
内聚力模型(cohesive zone model, CZM)克服了断裂力学不能预测裂纹萌生的缺点而受到越来越多的关注,并成功应用于单调载荷下的连接界面非线性断裂过程分析[13-15]。内聚力模型中表征裂纹萌生与扩展的主要参数为内聚强度和内聚力-位移曲线。相对于经验公式中的参数可变,当粘接面与胶层厚度相同时,同种材料的内聚力模型中的参数是不变的。因此通过少量试验测得模型参数后,模型可以应用于同类材料但负载严酷程度不同的情况,大幅节约成本。基于内聚力模型的上述优点,本文将其应用于振动载荷下的焊点疲劳模型,研究无铅焊点在振动载荷下的损伤演化规律,并将内聚力模型应用扩展到周期载荷情况,建立了在周期振动载荷下表征焊点累积损伤介观尺度模型。把焊点结构在介观尺度下抽象成两块基板,通过钎料薄层粘结在一起,焊点高度即粘结厚度,焊点失效可以表征为层间失效,用粘结面分离来表示。试验证明,通过少量试验确定焊点累积损伤参数后,该模型可用来预测相同钎料不同尺寸焊点在其他振动量级下的疲劳寿命,大大减少试验时间与成本。
1 振动载荷下内聚力模型的焊点累积损伤模型
1.1 焊点结构的内聚力模型
假设钎料内部无缺陷,焊点结构可抽象成层结构,为3部分:元件层、钎料层和PCB板的焊盘层。图1为SMT(surface mount technology)焊点组件模型示意图。
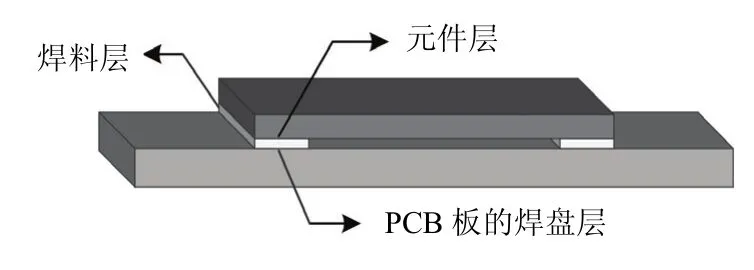
图1 SMT焊点组件简化几何模型Fig.1 Simplified geometric model of SMT solder joint
钎料层采用界面单元模拟,界面层相邻的元件层和焊盘层用连续实体单元模拟。图2为连接元件层与焊盘层之间的三维界面单元,由于界面层很薄,界面单元的上下表面之间的距离很小。坐标系中z方向为界面单元厚度方向,与I型裂纹相关;x、y方向为界面内相互垂直方向,与II、III型(剪切型)裂纹相关。
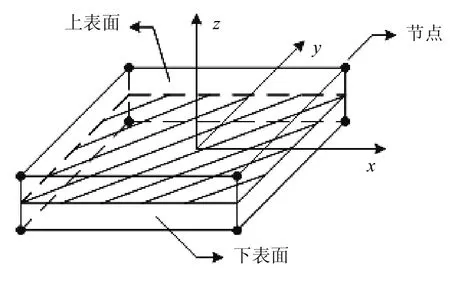
图2 三维界面单元Fig.2 Schematic diagram of the 3D interface element
当钎料层不存在损伤时,界面处的力学行为通常为线弹性的,界面应力矢量是界面处的名义应变的线性函数,如式(1)所示。
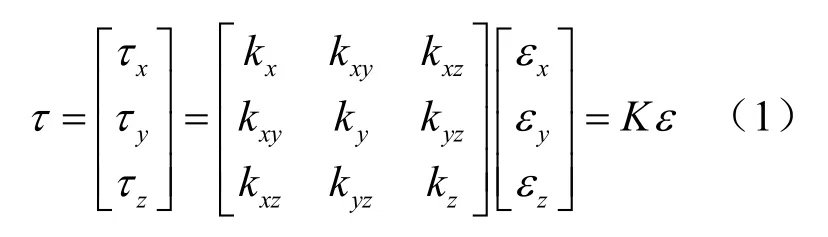
式中:K表示刚度矩阵。由于界面很薄,界面处法向形变很小,对切向形变影响也很小,这与已有研究表明切向应力应变是导致焊点裂纹产生的主要因素相吻合。因此可以对上述关系解耦,即刚度矩阵K中非对角元素为0,写成分量形式为
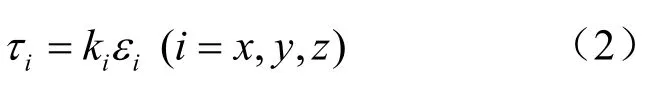
随着外界载荷施加到焊点,界面处会逐渐萌生裂纹并扩展。引入一无量纲损伤变量l表征在达到宏观裂纹之前界面损伤程度,在振动载荷下,定义钎料层杨氏模量变化率为损伤变量,如式(3)所示。

式中:E0表示钎料层无损伤的杨氏模量初始值;E为钎料层当前状态下的杨氏模量值。当=0时,表示钎料层没有损伤,不存在微裂纹与缺陷;当l=1时表示钎料层形成宏观裂纹。当钎料层产生微裂纹与缺陷时,界面的有效刚度为

式中:ki0为刚度初始值。随着损伤的累积,ki值逐渐降低。对于焊点而言,剪切应力应变是诱发焊点裂纹萌生与扩展的主要力学因素,因此主要考虑切向的应力应变,则剪切模式下界面间的内聚力为
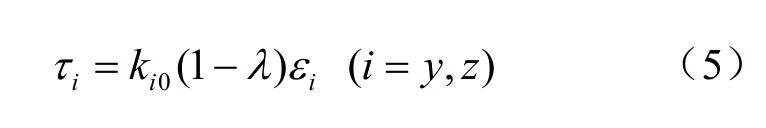
对于双线性关系的界面行为,式(5)表征的本构关系如图3所示,在界面达到内聚强度t0之前,内聚力与界面的相对位移是线性的。

图3 剪切型内聚力-相对位移曲线Fig.3 Curve of shear cohesive strength-relative displacement
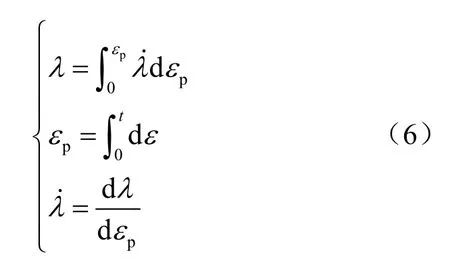
式中:ep为累积塑性切应变;为损伤累积率,用来表征焊点损伤演化规律。振动周期载荷与单调加载的最大不同之处在于损伤累积率不同。在单调加载情况下,能量耗散方向也为单向的,而在振动载荷下可能会产生反向的塑性变形,此时焊点内部晶粒产生的正向错位塞积会被释放,因此振动载荷下焊点的损伤累积率比单调加载情况下要小很多,这也是单调载荷下焊点的断裂应变要比振动载荷情况下小很多的原因。
当外部振动载荷施加到焊点时,负载首先由0逐渐增加到峰值,在振动周期的第一个半周期内焊点承受的实际为单调载荷,损伤累积率l&为单调加载情况下的,之后的振动周期内为周期载荷情况下的损伤累积率,显然这两者是关于塑性剪切应变的不同函数。图4为振动载荷下焊点累积损伤规律示意图。在阶段1,焊点在外加载荷下进入弹性无损伤阶段,此时钎料的杨氏模量为初始值E0。当到达弹性应变极限后,焊点开始发生塑性变形,损伤开始积累,内聚强度开始下降(阶段2),此时焊点损伤遵循的是单调载荷下的损伤演化规律。当外加负载达到最大值后开始卸载时,钎料的杨氏模量为,其中表征在阶段2焊点的累积损伤,内聚强度由0t减小为随着卸载的进行,焊点承受的载荷由正向转为负向(阶段3),开始发生反向塑性变形(阶段4),内聚强度和杨氏模量分别进一步减小为和当外部载荷到达最小值后又开始增加(阶段5),开始产生正向塑性变形(阶段6),焊点损伤进一步积累。随着振动循环次数的增加,当焊点损伤累积到阈值后,焊点失效。值得注意的是,在阶段2之后,焊点损伤开始遵循周期载荷下的损伤演化规律,阶段4和阶段6所产生的塑性变形对应于图4中的4’与6’。
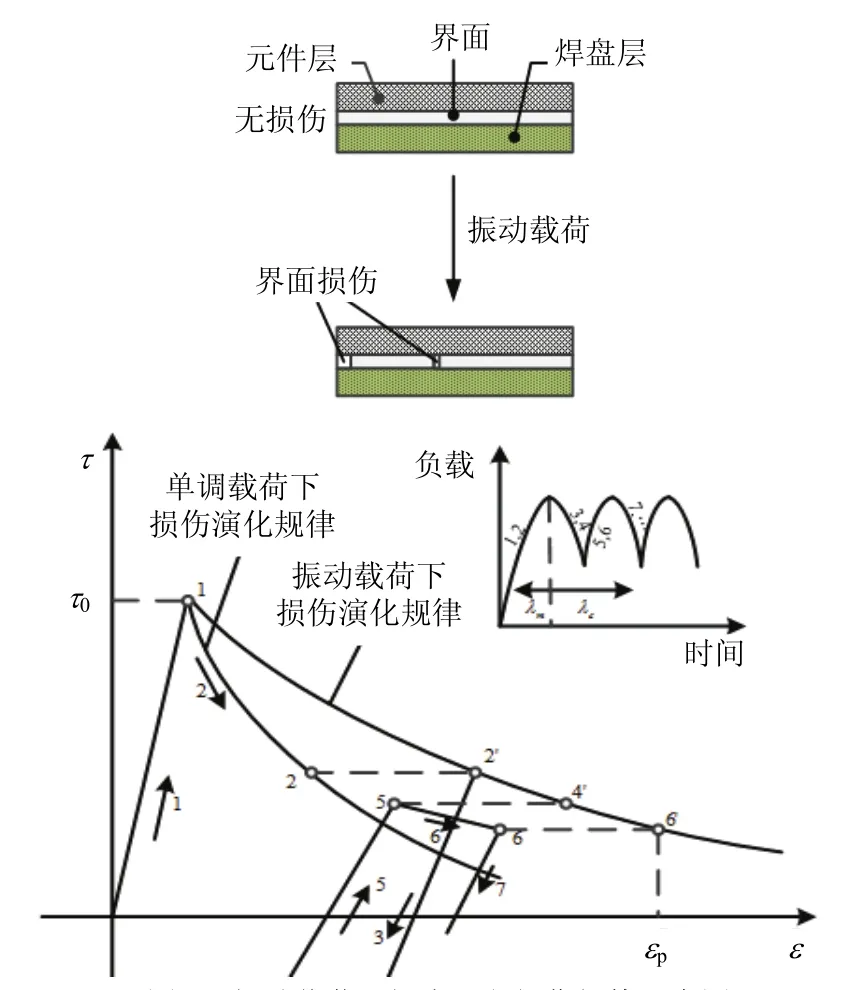
图4 振动载荷下焊点累积损伤规律示意图Fig.4 Schematic diagrams of solder joint accumulated damage law under vibration
1.2 无铅焊点损伤累积率的确定
试验选用的是QFP100型的方型扁平式封装,参考JESD22/B111标准设计制作电路板,如图5所示。所用钎料为Sn3.0Ag0.5Cu(SAC305),印刷电路板为镀Ni/Au层的FR-4基板,焊盘选用广泛使用的Au/Ni/Cu结构镀层焊盘。设计的试件芯片内部将引线连通形成菊花链,器件尺寸参数如表1所示。

图5 QFP试验组件Fig.5 Experimental components of QFP

表1 QFP器件尺寸Tab.1 QFP device dimensions
由于特种装备中电路板常采用单边插槽式连接方式,因此本研究采用类似的悬臂梁固支方式。利用拉伸试验法测量焊点的杨氏模量初始值为55 GPa。大量研究表明位于封装最外围边角处的焊点受到的应力应变最大,最先发生失效,因此利用散斑动态应变测量系统实时监测贴装器件边角焊点的背侧中心点在振动过程中的应力应变,通过PXI数据采集系统实时监测菊花链的边角焊点失效情况。
结合模态试验与有限元分析结果得到试验件的一阶共振频率约为30 Hz,因此分别进行频率为30 Hz、振幅为7.5mm的定频振动试验与加载速率为3mm/min的单调拉伸试验。试验中,用PXI数据采集系统监测边角焊点回路的电压值,通过判断其通断作为焊点疲劳失效的标准。图6为试验测得的焊点剪切应力与杨氏模量的变化量与塑性剪切应变的关系。可以发现经过归一化处理,两者的变化规律相似,因此将杨氏模量的改变作为焊点损伤的表征量是可行的。计算得出的损伤累积参数l与累积塑性剪切应变ep的关系如图7所示,焊点在l值达到0.93时发生疲劳失效。
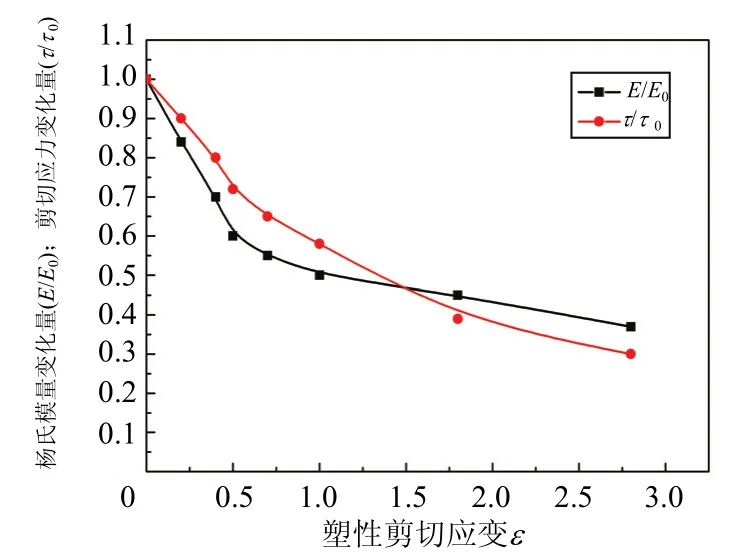
图6 杨氏模量、剪切应力与塑性剪切应变的关系图Fig.6 Relation schema of modulus/shear stress and plastic shear strain
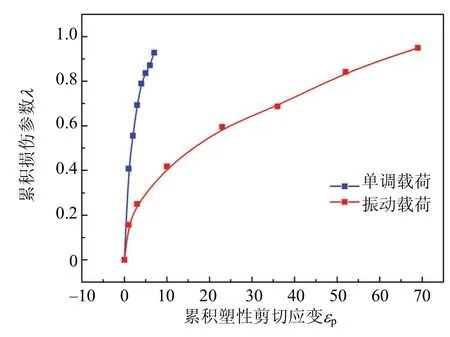
图7 累积损伤参数与累积塑性应变关系图Fig.7 Relation schema of accumulated damage parameter and accumulated plastic shear strain
通过对试验数据的拟合,SAC305焊点的损伤累积参数符合累积塑性剪切应变的幂律函数。l-ep函数关系为

则焊点的损伤累积率为

2 无铅焊点CZM模型预测性能验证
为验证模型预测SAC305焊点疲劳寿命的能力,选取同种钎料不同尺寸的焊点进行不同振动量级的试验。将l的阈值上限l设为0.9,即假设焊点累积损伤程度达到90%时,焊点开始发生疲劳失效。
(1)对QFP100器件进行振幅为5mm与10mm的定频振动试验,将2.2节计算所得模型的预测数据与试验实测数据进行对比,如图8所示。通过分析可知,表征焊点振动疲劳寿命的累积损伤参数l的CZM模型预测值与试验实测值基本吻合,在振动初期,焊点杨氏模量下降比较快,累积损伤参数增长明显,随后增长逐渐趋缓。在振幅为5mm时CZM模型预测值与实测值的最大误差为8.36%;在振幅为10mm时CZM模型预测值与实测值的最大误差为4.67%。焊点CZM模型在大应变条件下的预测精度更高。
(2)选择同种钎料、焊点几何尺寸不同的QFP64器件作为试验对象,进行频率为30 Hz、振幅为7.5mm的定频振动试验。CZM模型计算出的焊点寿命与试验数据对比如图9所示。可以看出,尽管焊点尺寸有差异,但由于累积损伤参数属于SAC305钎料的固有函数,焊点的几何尺寸对模型预测精度影响不大。

图8 不同振动量级下的试验数据与模型预测数据对比图Fig.8 Comparison diagrams of measured value and estimated value under different vibration levels
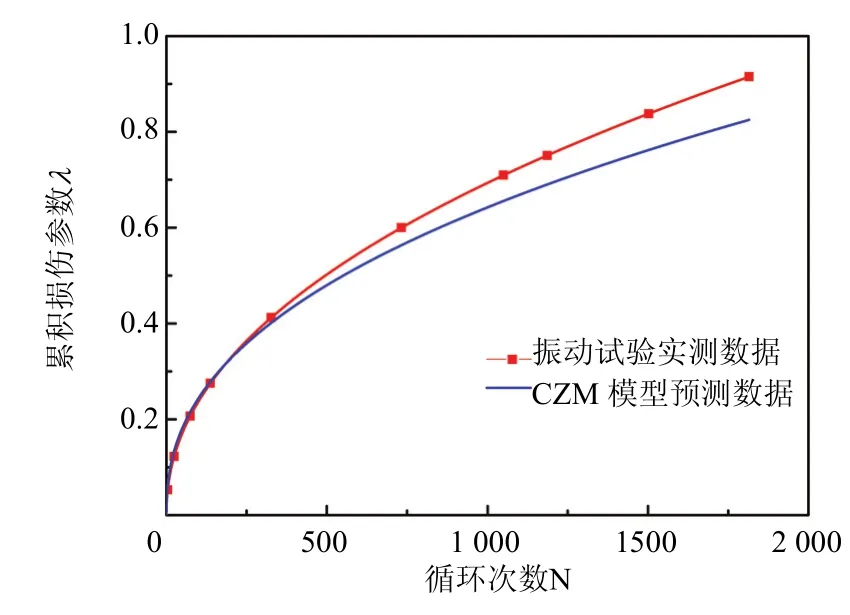
图9 QFP64器件焊点疲劳寿命预测图Fig.9 Fatigue life prediction of QFP64 component solder joints
3 结论
(1)基于内聚力模型,建立了振动载荷下SAC305细间距焊点疲劳寿命预测的介观尺度模型。将焊点承受的单调载荷与周期载荷统一起来,通过焊点累积损伤参数表征焊点疲劳寿命。
(2)焊点累积损伤参数为钎料层应变的固有函数,与焊点几何尺寸关系不大,因此可以在不修改模型参数的前提下,预测同种钎料不同几何形态焊点的疲劳寿命。
(3)由于模型参数通过小样本数据即可确定,能大幅节约试验时间和成本,该模型能为特种设备中电子组件的板级焊点疲劳寿命时提供一种简单实用的方法。
参考文献:
[1] PRADEEP L, PRASHANT G, ARJUN A. Anomaly detection and classification for PHM of electronics subjected to shock and vibration [J]. IEEE Trans Compon Packg Manuf Technol, 2012, 2(11):1902-1917.
[2] 刘洋, 张洪武, 孙凤莲, 等. 板级封装焊点振动冲击加速失效方法研究 [J]. 振动与冲击, 2013, 32(7):74-77.
[3] CHANGWOON H, CHULMIN O, WONSIK H. Prognostics model development of BGA assembly under vibration environment [J]. IEEE Trans Compon Packg Manuf Technol, 2012, 2(8):1329-1334.
[4] DA Y, ABDULLAH A Y, TUNG T N, et al. High-cycle fatigue life prediction for Pb-free BGA under random vibration loading [J]. Microelectron Reliab, 2011, 55:649-656.
[5] LEE J H, JEONG H Y. Fatigue life prediction of solder joints with consideration of frequency,temperature and cracking energy density [J]. Int J Fatigue, 2014, 61:264-270.
[6] TAKAEI Y, TAKAMOTO I, MASAO S, et al. Creep-fatigue life of Sn-8Zn-3Bi solder under multiaxial loading [J]. Int J Fatigue, 2012, 43:235-241.
[7] 徐文正, 任超, 罗成, 等. 带引脚表贴器件互联疲劳寿命的有限元分析 [J]. 电子元件与材料, 2014, 33(4):98-102.
[8] DELMONTE N, GIULIANI F, COVA P. Finite element modeling and characterization of lead-free solder jointsfatigue life during power cycling of surface mounting power devices [J]. Microelectron Reliab, 2013, 53:1611-1616.
[9] 何敏. PCBA结构参数与振动谱型对BGA焊点疲劳寿命的影响 [J].电子元件与材料, 2014, 33(3):81-85.
[10] 安彤, 秦飞. 跌落冲击载荷下焊锡接点金属间化合物层的动态开裂[J]. 固体力学学报, 2013, 34(2):117-123.
[11] WONG E H, SEAH S K W, SHIM V P W. A review of board level solder joints for mobile applications [J]. Microelectron Reliab, 2008, 48:1747-1758.
[12] PAYAM D, LEE T, THOMAS R B, et al. Crystal plasticity finite element study of deformation behavior in commonly observed microstructures in lead free solder joints [J]. Comput Mater Sci, 2014, 85:236-243.
[13] BAOMING G, MARCO P, ALBERTO C. A cohesive crack model coupled with damage for interface fatigue problems [J]. Int J Fract, 2012, 173(2):91-104.
[14] 徐杰, 雷刚, 曹建国, 等. 轿车车门焊点布置优化设计及仿真分析[J]. 重庆理工大学学报(自然科学), 2009, 11:25-28.
[15] 王永刚, 胡剑东, 王礼立. 金属材料层裂破坏的内聚力模型 [J]. 固体力学学报, 2012, 33(5):465-469.
(编辑:陈渝生)
Fatigue life prediction of board level solder joints for special equipment under vibration loads
XIE Xiaojuan
(Zhuhai Branch,Guangdong Insitute of Special Equipment Inspection and Research, Zhuhai 519000, Guangdong Province, China)
Abstract:A fatigue life prediction meso-scale model of board level solder joint was proposed for special equipment under vibration load based on cohesive zone model (CZM). Incorporating with monotonic and cyclic loadings, an accumulated damage parameter was constructed as an internal representation of solder joints’ residual fatigue life. So the damage accumulation law can be identified by a damage accumulation rate. Sn3.0Ag0.5Cu (SAC305) solder joints of fine pitch devices were taken as an example to determine the parameters of the model. The predictive capability of the model was verified by conducting constant frequency vibration tests whose amplitudes were 5mm and 10mm. The results indicate that the prediction error is less than 10%. The parameters are intrinsic functions of solder’s accumulated plastic strain and have nothing with the geometries of solder joints. Once the parameters of the CZM are calibrated by simple test configuration, the model can be used to predict the fatigue life of solder joints which is made of the same solder but with different geometries and loading conditions. So a great quantity of time and costs of experiments can be avoided. This method can be regarded as an analytical tool to evaluate the fatigue life of solder joints in practice.
Key words:vibration loads; cohesive zone model(CZM); accumulated damage parameter; board level solder joint; accumulated plastic strain; life prediction
doi:10.14106/j.cnki.1001-2028.2016.06.021
中图分类号:TN601;TH213.3
文献标识码:A
文章编号:1001-2028(2016)06-0098-05
收稿日期:2016-03-28
作者简介:谢小娟(1988-),女,广东珠海人,硕士,主要研究方向为特种设备检测,E-mail:841870360@qq.com 。
