二次锥规划方法在误差追踪投资组合中的应用*

白　颉，赵志国

(太原学院 数学系，山西 太原 030001)



二次锥规划方法在误差追踪投资组合中的应用*

白颉，赵志国

(太原学院 数学系，山西 太原 030001)

摘要:主要研究证劵投资组合中的误差追踪模型，并将此模型转换成二次锥规划模型，然后利用SDPT3软件来求解二次锥规划，以致解决误差追踪问题.

关键词:二次锥规划；投资组合；最优化方法

二次锥规划(SCOP)是锥规划的特例,它是在一个仿射空间和有限个二阶锥笛卡尔积的交集上求一个线性函数极小值或极大值的问题.作为数学规划领域的一个重要分支,二次锥规划的研究有非常重要的意义.二次锥规划有着广泛的应用背景[1-2],许多数学规划问题都可转化成二次锥规划求解[3],而且一般说来其效果要比转化成半定规划的效果好[4].因此近年来二次锥规划成为数学规划领域的一个值得关注的方向．由于其约束是非线性、凸、连续的,但并不连续可微,因此,二次锥规划是非光滑非线性凸规划问题.线性规划、凸二次规划和二次约束下的凸二次规划等都是二次锥规划的特例.二次锥规划应用广泛，其研究问题涉及控制、金融、组合优化、工程技术等诸多领域．而且许多数学问题均可转化为二次锥规划求解，如矩阵分式优化问题、双曲线约束问题、范数极小化问题等.

本文将二次锥规划模型及其求解方法应用于金融学中投资组合问题中，重点研究误差追踪投资组合问题.首先介绍二阶锥规划，包括二阶锥规划的标准形式和其对偶形式，进而构建误差追踪投资组合模型，并将其转化成二阶锥规划模型；最后给出数值算例，并用SDPT3实现且分析其结果.

1二次锥规划

二次锥规划的标准形式为[5]

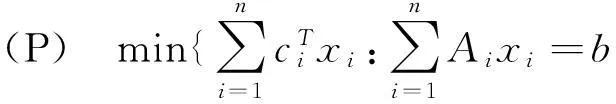
xi∈Ki,i=1,…,n}

(1)

其中,xi∈Ki(i=1,2,…,n)是变量，b∈Rm和Ai∈Rm×ki,ci∈RKi是已知量,Ki是维数为ki的二次锥,即

Ki=

{xi=(xi0,xi1)∈R×Rki-1:xi0-‖xi1‖≥0}

其中‖·‖是欧几里德范数.易知Ki是自对偶的，即

Ki=Ki*={si∈Rki:siTxi≥0,∀xi∈Ki}

且Ki的内部为

Ki0=

{xi=(xi0,xi1)∈R×Rki-1:xi0-‖xi1‖>0}二次锥规划的对偶规划为[6]

(D)max{bTy:AiTy+si=ci,

si∈Ki,i=1,…,n}

(2)

其中,y∈Rm为变量,si∈Ki,i=1,2,…,n为松弛变量.令k=k1+k2+…+kn,K=K1×K2×…×Kn,A=(A1,…,An)∈Rm×k,c=(c1,…,cn)∈Rk,x=(x1,…,xn)∈K，s=(s1,…,sn)∈K，

本文中Rk表示k维实列向量,Rk1×…×Rkn定义为Rk1+k2+…+kn，所以x=(x1,…,xn)∈K是Rk1+k2+…+kn中的列向量.那么问题(P)和(D)可分别简记为

(P)min{cTx:Ax=b,x∈K},

(D)max{bTy:ATy+s=c,s∈K}.

如果矩阵A是行满秩，且原SOCP的可行解是非空的，那么就存在一个向量x∈K使得Ax=b.基于对偶理论，求解SOCP的原对偶问题等价于解以下系统

(3)

方程组(3)是SOCP的最优条件.

2误差追踪投资组合模型

假设投资者选取n个资产，其收益率分别表示为S1,…,Sn,(n≥2).令μi和σi分别表示第i个资产的预期收益和标准差.当i≠j时,ρij表示Si和Sj的相关系数.令μ=(μ1,…,μn)T和∑=(σij)m×n为对称协方差矩阵，其中σij=σi2，并且当i≠j时，σij=ρijσiσj.假设xi表示第i个资产的投资资金，投资组合为x=(x1,…,xn)，其预期收益和方差为

E[x]=x1μ1+…+xnμn=μTx

和

假设投资者的预期目标以某个资产为参照物，如上证综合指数，这将产生跟踪误差，它是指投资组合的收益和基准之间的误差.假设xMB是基准组合的权向量，x是投资组合的权向量，那么这种误差为μTx-μTxBM=μT(x-xBM)．因此，投资者在跟踪误差不能超过一定范围的条件下，选择最优投资组合最大化预期收益，其模型表示为

(4)

下面将以上问题转换成二阶锥规划问题.由于∑是正半定，所以存在一个矩阵R使得∑=RRT.定义y=RTx，z=RTx-RTxBM.可以看到(4)中的前两个约束条件等价于(y0,y)∈C1，(z0,z)∈C2，其中，y0=σ,z0=TE.因此，模型(4)等价于下面的二阶锥规划模型(5)

(5)

3数值算例

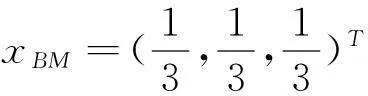
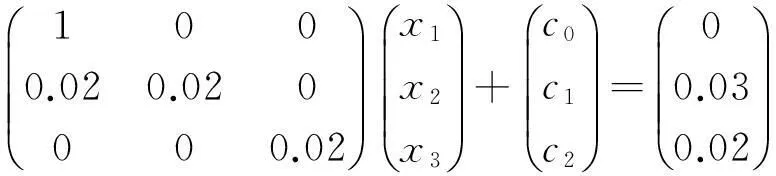
(c0,c1,c2)∈K3

(6)

y0=σ=0.032

其中,(y0,y1,y2)∈K1,(z0,z1,z2)∈K2,(c0,c1,c2)∈K3.

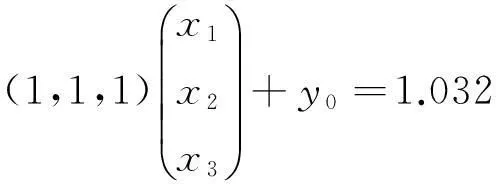
(7)

其中，(y0,y)∈K1,(z0,z)∈k2,(c0,c)∈K3.

用SDPT3-4.0软件，得到最优解为x1=0.6788,x2=0.0376,x3=0.2159;y0=0.1749,y1=-0.0115,y2=-0.0215;z0=-0.0215,z1=0.0057,z2=0.0044;c0=-0.0115,c1=0.0114,c2=0.0057.所以，在一些条件约束下投资者通过分别买三种股票的最优比例分别为x1=0.6788,x2=0.0376,x3=0.2159.

4小结

本文主要研究证劵投资组合中的误差追踪模型，并将此模型转换成二次锥规划模型，然后利用二次锥规划方法解决误差追踪问题.利用SDPT3-4.0软件，非常有效地解决我们的问题，且它的运算速度非常快.我们取得的研究结果为投资者，尤其是机构投资者，如基金公司，提供了选取最优投资组合的有效模型和方法，具有重要的应用价值.

参考文献：

[1]M S Lobo, L Vandenberghe, S Boyd, et al. Application of second order cone programming[J].Linear Algebra and Its Applications, 1998,284(3):193-228.

[2]Y J Kuo, H D Mlittelmann. Interior point methods for second order cone Programm and OR applieations[J].Computational Optimization and Applieations,2004,28(3):255-285.

[3]Z Q Luo. Applieations of convex optimizationin signal proeessing and digital communication[J].Mathematieal programming,2003,97(2):177-207.

[4]F H Clarke.Optimization and Nonsmooth Analysis[M].New York:John Wiley and Sons,1983.

[5]S Boyd, C Crusius, A Hansson. Control applications of nonlinear convex program ming[J].Journal of Proeess Control,1998,8(6):313-324.

[6]M Buss, H Hashimoto, J B Moore. Dextroush and grasping for optimization[J].IEEE Transactionson Roboties and Automation,1996,12(3):406-410.

(责任编辑:陈衍峰)

Application of the Second-order Cone Programming in Error Tracking the Portfolio Selection Problem

BAI Jie, ZHAO Zhi-guo

(DepartmentofMathematics,EducationInstituteofTaiyuanUniversity,Taiyuan,Shanxi030001,China)

Abstract:In this paper, the Error tracking model of Securities investment is mainly studied. Firstly, transform it into the second-order cone programming，then use SDPT3 software to solve the two cone programming , and lastly the rationality of the Model is tested by numerical example.

Key words:the second-order cone programming; Portfolio Selection Problem; optimization method

DOI:10.13877/j.cnki.cn22-1284.2016.06.013

*收稿日期：2015-12-20

基金项目：国家自然科学基金(71561008)

作者简介：白颉,女,山西吕梁人,讲师.

中图分类号：O221

文献标志码：A

文章编号：1008-7974(2016)03-0036-03