互联网拍卖的一类最优拍卖机制研究
2016-07-21陈龙
陈 龙
(攀枝花学院数学与计算机学院,四川攀枝花 617000)
互联网拍卖的一类最优拍卖机制研究
陈 龙
(攀枝花学院数学与计算机学院,四川攀枝花 617000)
[摘 要]以Onsale网上拍卖公司为背景,在拍卖总供给给定的条件下,基于网上拍卖数量对报酬函数影响的若干重要理论,将拍卖时间视为变量,改进了拍卖时间确定的方法,得出了获取最优利润的一类新的最优拍卖机制的设计方法。
[关键词]网上拍卖;最优机制;互联网
传统的商品交易通常是以固定价格的方式出售商品,但对顾客来讲,这种购买方式受到时间、空间等因素的限制。随着互联网的发展,已有许多商家将他们的产品推上网络,并以更快、更灵活、更方便的方式出售,使顾客足不出户选购商品成为了现实。近几年有关网上拍卖时间的研究有了一些新的进展。Lucking-Reiley[1]等通对过钱币拍卖的研究,提取eBay上的数据,发现拍卖时间的长短与商品的成交价格高低有关。Pinker[2]等指出:如果拍卖商把拍卖时间定得太长,买卖双方的额外成本会增加。Marcoux[3]讨论了如何选择最优拍卖结束时间规则。Bajari[4]等也以eBay为调查对象,发现在网上拍卖中拍卖方的期望收入与顾客的数量有密切关系。另外,拍卖方的声誉也是相当重要的,但顾客的投标经验对拍卖收入的影响并不大。
本文从定量的角度,以全球最大的网上拍卖公司——美国的Onsale公司为例,利用互联网以拍卖形式销售的商品为背景,讨论了商家如何设计拍卖机制才能在有效进行资源配置的基础上获得最大利润的问题。
1 模型的设立与前提
美国Onsale网上拍卖公司的拍卖规则设计十分复杂。假定商家拍卖t天使得商家的利润最大,每天每件产品的存贮费用为h元,若拍卖到达的顾客数nt=n(0≤n<∞),顾客的报价分别为r1,r2……rn,其从大至小依次重新排列得到b1≥b2≥……≥bn。
现作以下6个假定:
1)投标顾客的到达过程是参数为λ的泊松过程;
2)顾客都是风险中性的;
3)顾客的报价是相互独立的;
4)每个顾客最多只能买一件商品;
5)商家对拍卖品的保留价为零;
6)顾客是信息对称的,即双方掌握的信息是相同的,且他们的报价在[a,b]上均匀分布,其分布函数记为F(x)[1-3]。由于参与投标的顾客到达是参数为λ的泊松过程,其分布函数为
2 单物品拍卖的最优拍卖时间确定
2.1模型建立
令b1为商品的第一最高报价,由全概率公式得
由于F(x)是 [a,b]上的均匀分布,不难看出b1取值于 [a,b],于是商品的第一最高报价的期望为
若记r(i,t)表示在t时间内拍卖出i件产品所获得的报酬,从而商家获得的报酬为r(1,t)。
要使r(1,t)最大,求稳定点
商家拍卖一件商品时,其拍卖时间t满足式(3)时,商家的利润最大[4-9]。
2.2数值分析
由文献[10]得来的数据对最优化问题进行求解,根据Carrie Bean等对Onsale网站上拍卖的CD机进行统计,确定他们的参数值为:
1)每件商品每天的固定存贮费h=0.13美元;
2)顾客每天的到达率λ=13.6;
3)顾客的报价在[75,150]美元之间服从均匀分布,故a=75,b=150。
代入式(3),即得:拍卖一件该商品,拍卖时间定为t=7 d时,拍卖商的期望利润最大。
3 多物品拍卖的最优拍卖时间确定
3.1模型建立
如何确定拍卖时间的长短,从而使商家获得的期望利润最大。除了前面假定的条件以外,另假定每个顾客最多只能购买一件商品。拍卖到达的顾客人数nt=n(0≤n<∞),由于参与投标的顾客到达是服从参数为λ的泊松过程,其分布函数为
r1,r2……rn分别为顾客的报价,根据假设,报价r1,r2……rn是在 [a,b]上均匀分布的随机变量,且相互独立,令b1,b2……bn为r1,r2,……rn从大到小排列后的报价,即:b1≥b2≥……≥bn。
1)当n 2)当n≥k时,令bk为商品的第k最高报价。 由式(4)和式(5)得 由于F(x)是 [a,b]上的均匀分布,不难看出bk取值于 [a,b],于是商品的第k个最高报价的期望值E[bk]为 从而商家获得的报酬为 要得到最优的时间t,就要满足方程 即满足 只要t满足式(7),商家的期望利润最大。式(7)中,k是商家拍卖的商品数;[a,b]是投标商的估价范围;λ是顾客每天的到达率;h是每天每件拍卖品的存贮费用。对具体的商品,一旦k,a,b,λ,h确定,最优拍卖时间t就能通过式(7)获得[11-13]。 3.2数值分析 由文献[10]得来的数据对式(7)中最优化问题进行求解,根据Carrie Bean等对Onsale网站上拍卖CD机的统计,他们确定的参数值为: 1)每件商品每天的固定存贮费h=0.13美元; 2)顾客每天的到达率λ=13.6; 3)顾客的报价在[75,150]美元之间服从均匀分布,故 拍卖品的数量和拍卖时间长短如表1所示(表内的拍卖时间为通过四舍五入后的数据),拍卖商的期望利润最大。 由表1可知,当h=0.13美元,λ=13.6,a=75美元,b=150美元时,当商家拍卖2件商品时,拍卖时间定为8天,商家的期望利润最高;当商家拍卖3件商品时,拍卖时间定为9天,商家的期望利润最高;当商家拍卖4件商品时,拍卖时间定为10天,商家的期望利润最高等等。 表1 最优拍卖时间Table 1 The optimal auction time 3.3模型优化 商家对拍卖品的保留价为零这一假设一般情况下是不成立的。由于拍卖品的价值、成本等因素,它的最低价常常不等于零,因而商家都会事先给拍卖品制定一个保留价v,即低于这个价格不予出售[14-15]。 下面我们讨论在商家设置不公开保留价v的情况下,如何确定最优拍卖时间,使得拍卖商的期望利润最大化。除了前面假定的条件以外,另假定k件拍卖商品全部拍卖出去,此时到达的顾客数也必定大于拍卖出的商品数量,即n≥k,并且到达的n位顾客的报价中至少有k个报价不低于v。 计算报酬函数r(k,t),即bk为顾客报价中第k个最高报价,k≥1。由于拍卖出的商品数不可能大于到达的顾客数,所以记n 在n≥k的条件下,自然有bk∈ [a,b],由全概率公式得 由式(8)和式(9)可得 由此可知,当k≥1,顾客的第k个最高报价bk是一个连续型和离散型相结合的随机变量,其分布函数为 由于商家设有保留价v,所以这里仅需考虑顾客与商家成交时的价格,我们称之为成交价。当k≥1,第k个成交价就是当bk≥v时的第k个最高报价bk。于是,商品的第k个最高成交价的期望值为 由式(10)可得 对c>0,用分部积分递推可求得 将上式代入式(13)可得 将式(10)、式(14)代入式(12),得到商品的第k个最高成交价期望值为 从而商家获得的报酬为 要得到最优时间t,就要满足方程 只要t满足式(16),商家的期望利润最大。式(16)中,k是商家拍卖的商品数;[a,b]是投标商的估价范围;λ是顾客每天的到达率;h是每天每件拍卖品的存贮费用;v是拍卖商的保留价。对具体商品,一旦k,a,b,λ,h,v确定,最优拍卖时间t就能通过式(16)获得。 本文以美国Onsale网上拍卖公司为例,对网上一次性英式拍卖进行了具体分析,只要拍卖时间的长短选择合适,商家可以提高他的期望利润,并且在这个基础上对模型进行优化,即假设拍卖商设置了保留价v的情况下,最优拍卖时间的确定更有其现实的指导意义。但是文中没有分析分阶段拍卖,如果分阶段拍卖,每个阶段拍卖时间的长短也会影响商家的阶段期望利润,从而影响到商家的总期望利润,所以如何确定每个阶段的拍卖时间,制定出有利于商家网上拍卖的最优机制,笔者将在后续工作中进一步进行研究。 [参考文献] [1] Lucking-Reiley D,Bryan D,Prasad N,et al.Pennies from eBay:The determinants of price in online auctions[J].Working paper,Vanderbilt University,Nashville,TN,1999,38(21):998-1023. [2] Pinker E J,Seigmann A,Vakrat Y.Managing online auctions:Current business and research issues[J].Management Science,2003,49(11):1457-1484. [3] Marcoux A M,Snipers,stalkers,et al.Online auction business ethics[J].Journal of Business Ethics,2003,46(2):163 -176. [4] Chamberlin E H.An Experimental Imperfect Market[J].Journal of Political Economy,1948(56):95-108. [5] Smith V L.Microeconomic Systems as an Experimental Science[J].American Economic Review,1982,72(13):923-955. [6] 詹文杰,汪寿阳.评“Smith奥秘”与双向拍卖的研究进展[J].管理科学学报,2003,6(1):1-9. [7] Engelbrecht-wiggans R.Auctions and Bidding Models:a Survey[J].Management Science,1980,26(2):119-142. [8] McAfee R P,McMillan J.Auctions and Bidding[J].Journal of Economic Literature,1987,25(2):699-738. [9] Maskin E S,Riley J G.Auction Theory with Private Values[J].American Economic Review,1985,75(2):150-155. [10] Vickrey W.Counter speculation,Auctions,and Competitive Sealed Tenders[J].Journal of Finance,1961,16(1):8-37. [11] Bean C,Segev A,Shanthikumar J G.Electronic Negotiation[J].Throug Internet based Auction,1998,47(6):136-157. [12] 唐小我,陈绍刚,赵蜀蓉.招标与拍卖过程中的投标人数的研究[J].中国管理科学,2003,11(5):27-29. [13] 安勇,陈绍刚,赵丽霞.基于随机估值的最优保留值设置[J].电子科技大学学报,2004,33(3):316-318. [14] 陈绍刚,赵蜀蓉.基于随机估值的两物品拍卖的投标决策[J].电子科技大学学报,2002,31(4):43-47. [15] 杜黎,胡奇英.网上拍卖品书数量的优化[J].西安电子科技大学学报:自然科学版,2003,1(1):20-25. (责任编辑 柴 智) A Study on Optimal Mechanism of Internet Auctions Chen Long Abstract:Based on the auction formalism in onsale,Inc.,an Internet-based auction house.Under the condition of given supplies,based on the theory of influence of on-line auction quantity to the reward function,regards the auction time as the variable,improved the determination methods of the auction time,and obtained some new thoughts about how to obtain the optimal interest.This paper investigatesa type of optimal problems of internet auctions in the context of Onsale Internet Auction Corporation.In the setting,auction time is described as a random variable.When given the total auction supplies,by applying some important results of reward functions disturbed by the number of internet auctions,this paper improves the method of determining auction time and by finding optimal profit,obtains a new type design for auction mechanism. Key words:On-line auction;The optimal mechanism;Internet [中图分类号]F 713.359 [文献标志码]A [文章编号]1005-0310(2016)01-0065-07 DOI:10.16255/j.cnki.ldxbz.2016.02.12 [收稿日期]2014-10-14 [基金项目]攀枝花学院科研项目(2013YB12)。 [作者简介]陈龙(1981-),男,四川省遂宁市人,攀枝花学院讲师,主要研究方向为数论及经济数学。E-mail:scsnchl @126.com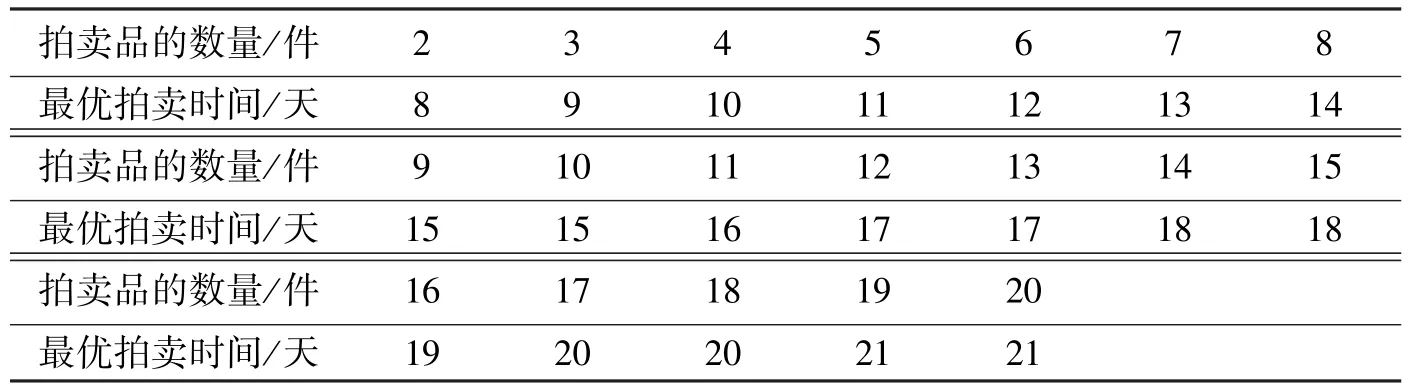
4 结束语
(School of Mathematics and Computer Science,Panzhihua University,Panzhihua Sichuan 617000,China)
