基于二维Arimoto灰度熵的图像阈值分割快速迭代算法*

吴一全　朱丽　吴诗婳

(1.南京航空航天大学 电子信息工程学院，江苏 南京 211106； 2.江苏省制浆造纸科学与技术重点实验室，江苏 南京 210037；3.中国水产科学研究院淡水渔业研究中心 农业部淡水渔业与种质资源利用重点实验室， 江苏 无锡 214081；4.农业部东海海水健康养殖重点实验室，福建 厦门 361021)



基于二维Arimoto灰度熵的图像阈值分割快速迭代算法*

吴一全1,2,3,4朱丽1吴诗婳1

(1.南京航空航天大学 电子信息工程学院，江苏 南京 211106； 2.江苏省制浆造纸科学与技术重点实验室，江苏 南京 210037；3.中国水产科学研究院淡水渔业研究中心 农业部淡水渔业与种质资源利用重点实验室， 江苏 无锡 214081；4.农业部东海海水健康养殖重点实验室，福建 厦门 361021)

摘要:现有的Arimoto熵阈值法仅依赖于灰度直方图分布,且计算最佳阈值时需搜索整个解空间,效率不高.为此,文中提出了一种二维Arimoto灰度熵阈值分割的快速迭代算法.首先,提出了一维Arimoto灰度熵阈值选取的快速迭代算法;然后,考虑图像目标和背景的类内灰度均匀性,导出了基于灰度-平均灰度级直方图的Arimoto灰度熵阈值法,并给出了中间变量的快速递推公式;最后,提出了二维Arimoto灰度熵阈值选取的快速迭代算法,推导了相应的公式,大大减少了运算量.实验结果表明,文中所提算法运行速度快,分割性能优于现有的5种同类阈值分割算法,分割后图像中的目标完整,边缘纹理清晰,细节更为丰富.

关键词：图像分割；阈值选取；二维Arimoto灰度熵；快速迭代算法

图像分割是图像处理的前期关键技术之一.阈值分割因其简单实用而成为常用的图像分割方法,其关键是快速得到合适的阈值以将图像中的目标和背景分离.至今人们已经提出了多种阈值分割方法[1- 6],其中Kapur等[4]提出的最大Shannon 熵阈值选取方法备受关注,Abutaleb[5]将这种最大Shannon熵法从一维拓展到了二维,对含噪图像的分割效果比一维方法有了显著的提高,但计算量大幅增加,实时性较差.为此,人们提出了二维最大Shannon熵法的快速算法[7- 9],但快速算法所需存储空间依然较大,影响阈值搜寻速度.有鉴于此,吴成茂等[10]采用快速迭代算法来改进二维Shannon熵阈值法,缩小了搜寻空间,并提高了运行速度.由于Shannon熵定义在对数函数基础上,故存在零点处无定义值的问题,且Shannon熵阈值法会忽略目标与背景灰度分布间的相关性.为了弥补Shannon熵的上述缺陷,人们提出了基于Tsallis熵的二维阈值分割法[11- 13],并取得了一定的成果.近年来,人们将Arimoto熵引入阈值分割,Arimoto熵是一种能有效处理决策误差，得到误差概率上界的广义熵[14].基于此,文献[15- 16]提出了二维Arimoto熵阈值法,但二维Arimoto熵仅依赖于二维灰度直方图的概率信息,没有兼顾图像类内的灰度均匀性.因此，二维Arimoto熵阈值法对某些图像的分割效果不佳.文献[17]提出了一维Arimoto灰度熵,将灰度信息引入Arimoto熵,解决了灰度均匀性问题.与一维阈值分割法相比,二维阈值法的分割精度更高,然而其运行速度却大大降低.人们通常采用快速递推公式来减少计算过程所需的存储空间并降低计算复杂度.

为了进一步缩短Arimoto熵阈值分割的运行时间,文中在推导出一维Arimoto灰度熵阈值选取的快速迭代算法公式的基础上,提出了二维Arimoto灰度熵阈值分割的快速迭代算法;针对灰度级-邻域平均灰度级二维直方图,应用Arimoto灰度熵构成新的Arimoto灰度熵阈值选取公式,推导了基于灰度级-邻域平均灰度级直方图的Arimoto灰度熵阈值选取快速迭代算法公式,并通过引入迭代过程、缩小搜索空间、在迭代中采用递推法降低冗余计算来加快算法的运行速度;最后将实验结果与现有同类算法进行了比较.

1一维Arimoto灰度熵阈值选取的快速迭代

1.1一维Arimoto灰度熵阈值选取

Arimoto熵定义为

(1)

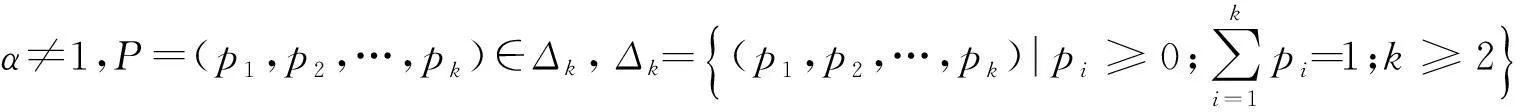
Arimoto熵具有准可加性的特点,即若随机变量X与Y相互独立,那么

(2)

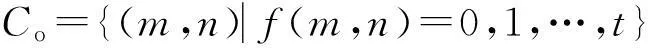
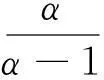
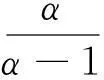
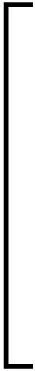
(3)

(4)

1.2一维Arimoto灰度熵阈值法的快速迭代算法

通过Arimoto灰度熵阈值法的分割准则(见式(4))获得图像分割的最佳阈值t*,其传统做法是:t在1～L-1之间取值，求函数Hα(t)取得最大值时所对应的t值.鉴于这一搜索过程需要花费大量的时间,文中提出了一种快速迭代算法,具体推导过程如下.

假设图像的灰度直方图连续,且概率密度函数为p(x),给定阈值t将原图像分割成目标和背景两部分,依据式(3),基于一维Arimoto灰度熵的图像阈值分割准则为

令vo(t)=∫0tp(x)xαdx,uo(t)=∫0tp(x)xdx,

vb(t)=∫tL-1p(x)xαdx,ub(t)=∫tL-1p(x)xdx,

则分割准则变为

(5)

(6)

根据式(6)构造基于一维Arimoto灰度熵的快速迭代算法,求得图像分割的最佳阈值t*,具体步骤如下:

(1)选取初始阈值t(可选灰度级的均值或中值),给定允许误差ε,初始化最大迭代次数Cmax,令k=0;

(2)t(k)=⎣t(k)」,计算vo(t(k)),vb(t(k)),uo(t(k)),ub(t(k));

(3)根据式(6)更新t*,计算e(t(k))=t*-t(k);

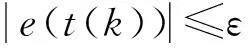
(5)t(k+1)=t*,k=k+1,若k>Cmax,则转步骤(6),否则转步骤(2);

(6)输出最佳阈值t*并结束.

2二维Arimoto灰度熵阈值选取的快速迭代

2.1二维Arimoto灰度熵阈值选取

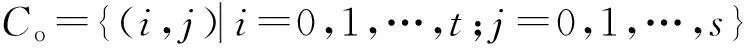
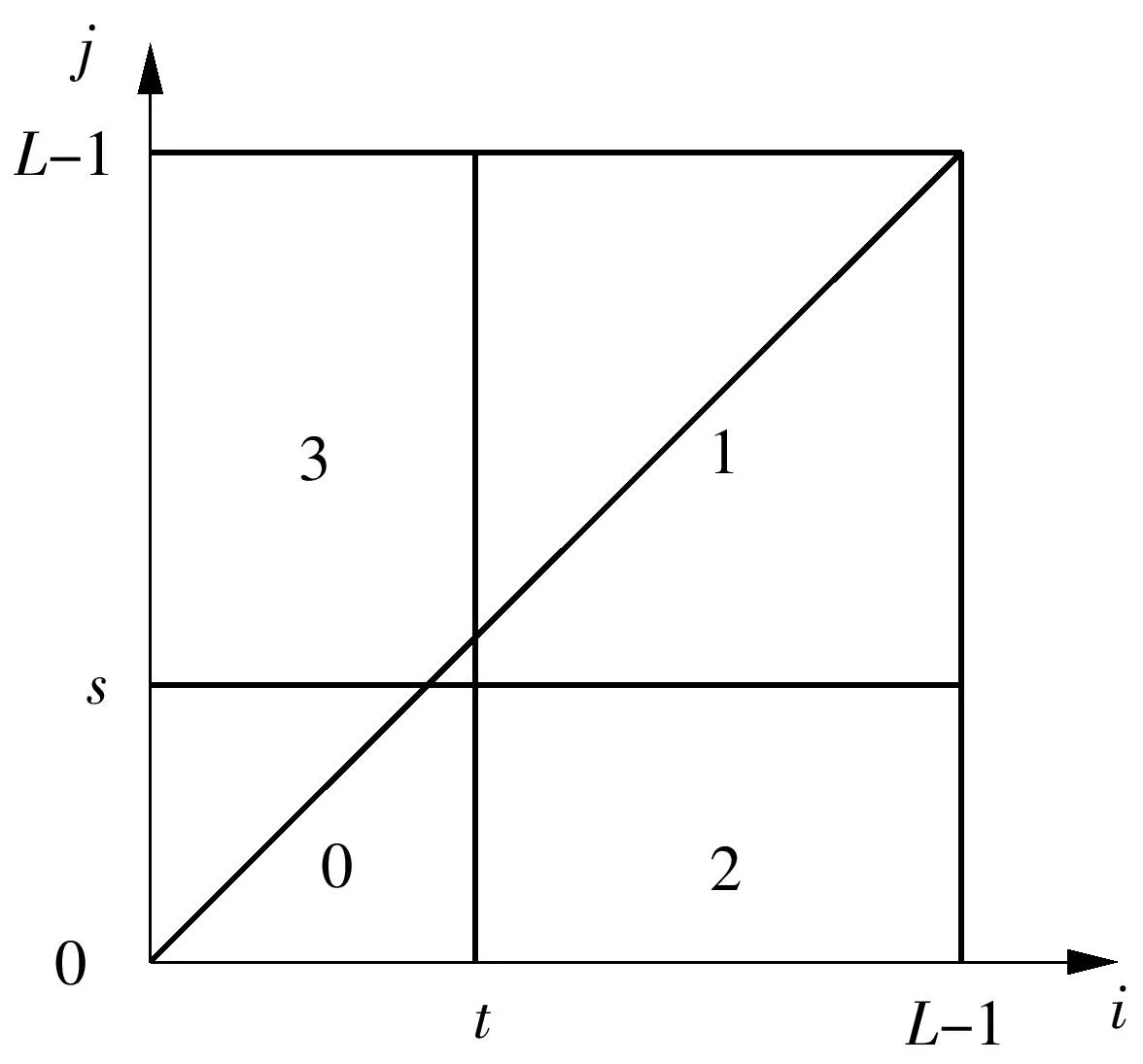
图1　二维直方图的区域划分

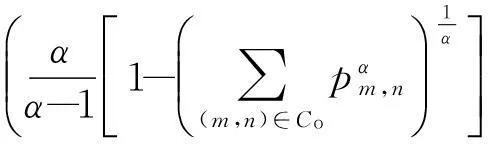
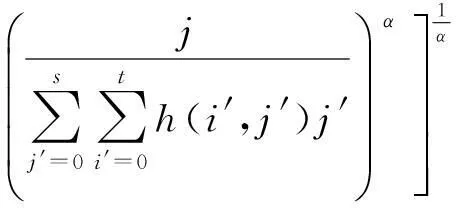
(7)

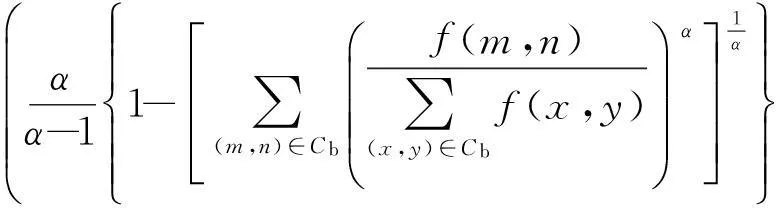
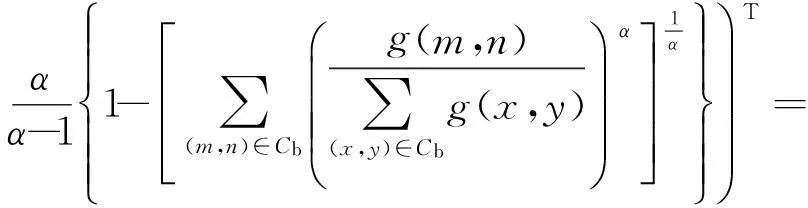
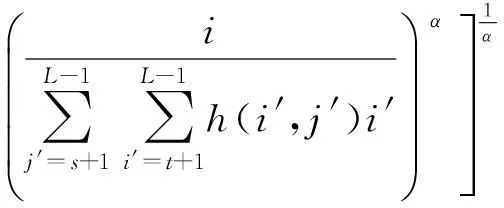
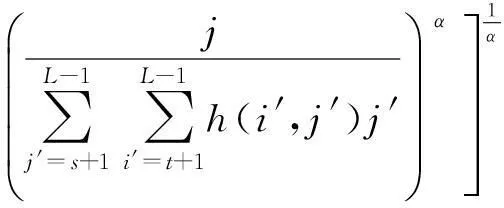
(8)

目标类和背景类的总Arimoto灰度熵Hα(t,s)为

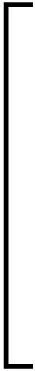
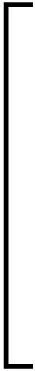
(9)

定义二维Arimoto灰度熵阈值法的准则函数ξ(t,s)为

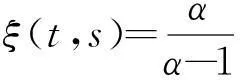
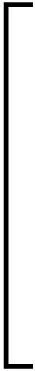
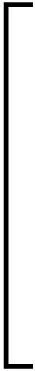
(10)

令

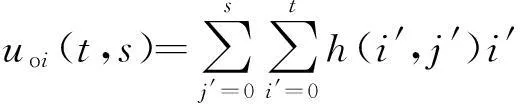
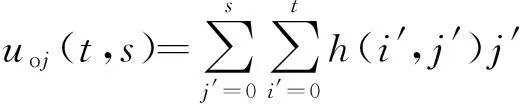
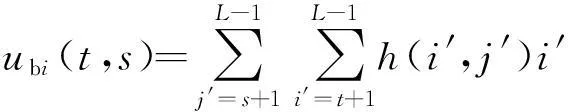
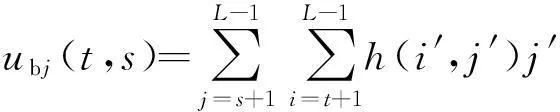
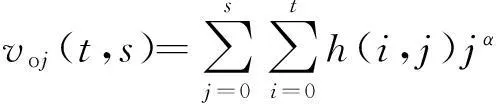
则有

(11)

当ξ(t,s)取得最大时，可得到最佳阈值向量(t*,s*):

(12)

2.2二维Arimoto灰度熵阈值法的快速迭代算法

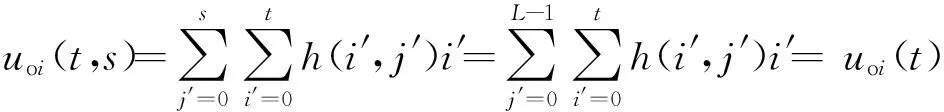
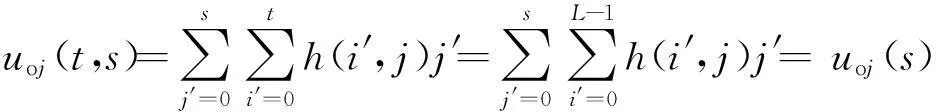
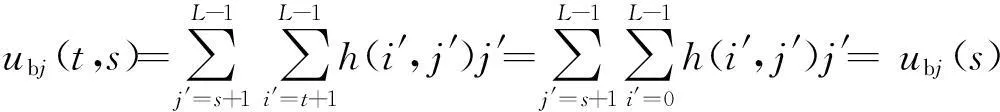
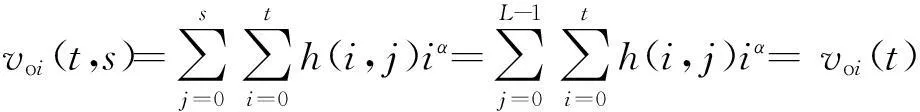
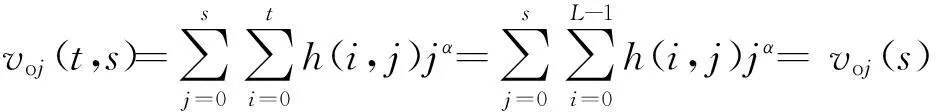
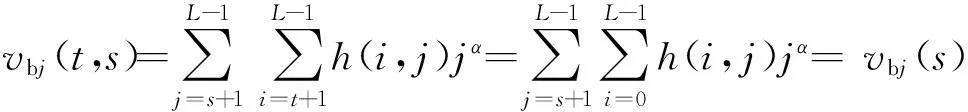
ηi(t)+ηj(s)

(13)

判别函数

ηi(t*)+ηj(s*)

(14)

式(13)中A项仅含待定阈值参数t,与s无关;而B项仅含待定阈值参数s,与t无关.选择判别函数ξ(t,s)最大所对应的阈值向量作为二维Arimoto灰度熵阈值法的最佳阈值向量(t*,s*).为此,对式(13)分别求关于t和s的偏导数并令其为0,即

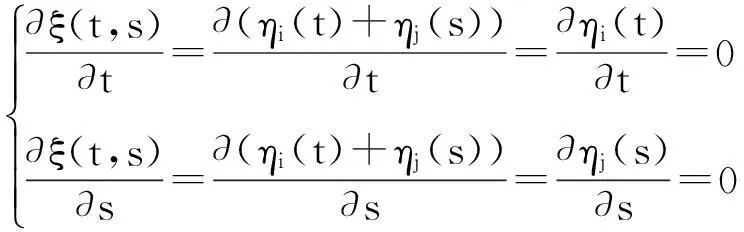
求解可得

(15)

3算法流程和实现步骤

文中提出的二维Arimoto灰度熵阈值分割快速迭代算法流程如图2所示.

图2　文中算法流程图

算法实现的具体步骤如下:

(1)建立查找表.设Vi和Hj分别表示像素灰度级和邻域平均灰度级的边缘分布,则由(f(m,n),g(m,n))二元对出现的频数h(i,j)可得

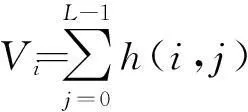
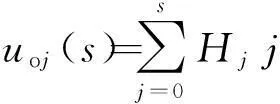
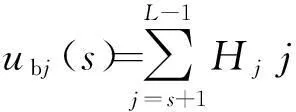
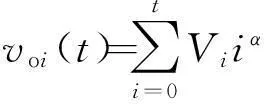
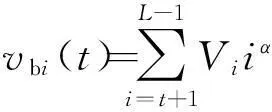
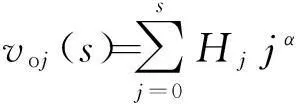
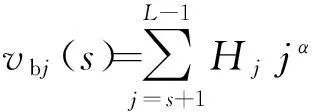
在计算Vi、Hj时,为减少迭代过程中有关函数的重复计算,缩短运行时间,可建立如下查找表

然后用递推方式计算w(k,l),可大大减少算法的运行时间,即

w(k,l)=w(k-1,l)+w(k,l-1)-

w(k-1,l-1)+h(i,j),

则Vi=w(i,L-1),Hj=w(L-1,j).

uoi(t)=uoi(t),ubi(t)=uoi(L-1)-uoi(t),

uoj(s)=uoj(s),ubj(s)=uoj(L-1)-uoj(s),

voi(t)=voi(t),vbi(t)=voi(L-1)-voi(t),

voj(s)=voj(s),vbj(s)=voj(L-1)-voj(s).

(3)根据式(15)计算阈值向量(t,s).

4实验结果和分析

利用文中提出的一维Arimoto灰度熵阈值选取的快速迭代算法、基于灰度级-平均灰度级二维Arimoto灰度熵阈值选取的快速迭代算法,针对不同类型的灰度图像进行了大量的阈值分割实验,将实验结果与一维Arimoto熵法[14]、一维Arimoto灰度熵法[17]、文中一维Arimoto灰度熵迭代法、二维Arimoto熵法[15]、二维Arimoto熵直线型阈值法[16]以及改进二维Arimoto灰度熵法[17]进行了比较.实验运行环境如下：Microsoft Windows 7,Intel(R) Core(TM) 2 Duo CPU7350内存2 GB,Matlab7.11.因篇幅有限,文中仅给出了4幅图像(纸张纤维图像,2 048×1 536;裂痕图像,352×288;破洞图像,156×157;淡水鱼图像,976×362)的分割结果(如图3-6所示)、最佳阈值及运行时间(如表1所示).

从图3可以看出:7种阈值分割法均能分割出纸张纤维,但一维Arimoto熵法[14]、二维Arimoto熵法[15]、二维Arimoto熵直线型阈值法[16]及改进二维Arimoto灰度熵法[17]均丢失了大量的目标信息,无法准确地分割出灰度级较高的纤维;一维Arimoto灰度熵法[17]存在过分割现象,文中二维Arimoto灰度熵快速迭代法能准确获取所有的目标纤维,且目标和背景的细节最为清晰.从图4可以看出,一维Arimoto熵法[14]、一维Arimoto灰度熵法[17]、文中一维Arimoto灰度熵快速迭代法、二维Arimoto熵法[15]、二维Arimoto熵直线型阈值法[16]以及改进二维Arimoto灰度熵法[17]都存在不同程度的过分割,而文中提出的二维Arimoto灰度熵快速迭代法能清晰、完整地分割出裂痕,为后续纸张缺陷图像的特征提取与识别奠定了良好的基础.从图5可以看出,文中提出的二维Arimoto灰度熵快速迭代法的分割结果优于其他6种方法,破洞的毛刺清晰完整,细节信息更为丰富.

图4　裂痕图像的分割结果

图5　破洞图像的分割结果

图6　淡水鱼图像的分割结果

从图6可知:采用一维Arimoto熵法[14]、一维Arimoto灰度熵法[17]及改进二维Arimoto灰度熵法[17]时,鱼的边界处丢失了一些信息,且边界与背景无法区分,不利于后续的鱼体轮廓提取;采用文中一维Arimoto灰度熵快速迭代法、二维Arimoto熵法[15]及二维Arimoto熵直线型阈值法[16]时,鱼体的边界能与背景很好地区分,但鱼体背部的纹理不够清晰,降低了后续淡水鱼的分类精度;采用文中提出的二维Arimoto灰度熵快速迭代法算时,鱼体轮廓清晰,且获得了更多的纹理细节.

从表1可以看出:文中提出的二维Arimoto灰度熵快速迭代算法得到最佳阈值所需要的时间只有二维Arimoto熵法的10%.一方面是因为文中采用迭代算法计算图像阈值,可大幅缩小计算最佳阈值时的搜索范围和所需的存储空间,使求解二维Arimoto灰度熵阈值法的运算转化到两个一维空间上,计算复杂度从O(L4)降低为O(L),从而降低了计算量,提高了算法的运算速度;另一方面是由于文中采用递推方式建立查找表,大大减少了迭代过程中有关函数的重复计算,使算法迭代一次的速度更快.

为了说明文中提出的二维Arimoto灰度熵快速迭代算法的普适性与有效性,选取Weizmann分割评价数据库中的100幅灰度级图像,采用文中算法进行了大量的阈值分割实验.分割准确率定义为正确分割的像素数与像素总数的比值,正确分割的像素数是指分割后的图像与经人工精细分割后的标准图像相比一致的像素个数,像素总数是指灰度级图像中目标类和背景类的像素个数之和.分割准确率越高,表示误分割程度越小,分割结果越准确.实验结果表明,文中算法对不同类型灰度级图像的分割准确率均大于90%,运行时间远小于0.5 s.因此,从主观视觉效果及分割准确率、运行时间等定量评价指标来看,文中算法的分割结果更准确,运行速度更快,且具有良好的普适性.

5结论

文中在推导出一维Arimoto灰度熵阈值选取的快速迭代算法公式的基础上,提出了二维Arimoto灰度熵阈值分割的快速迭代算法,针对灰度级-邻域平均灰度级二维直方图,应用Arimoto灰度熵构成新的Arimoto灰度熵阈值选取公式,推导了基于灰度级-邻域平均灰度级直方图的Arimoto灰度熵阈值选取快速迭代算法公式,并通过引入迭代过程、缩小搜索空间、在迭代中采用递推法降低冗余计算来加快算法的运行速度.与一维Arimoto熵法、一维Arimoto灰度熵法、二维Arimoto熵法、二维Arimoto熵直线型阈值法及改进的二维Arimoto灰度熵法相比,文中提出的二维Arimoto灰度熵阈值分割的快速迭代算法能使分割后的图像边界形状更接近原始图像,细节纹理特征更加清晰,所需的运行时间大约为二维Arimoto熵法的10%,是实际工程中可以选择的一种快速有效的阈值分割算法.

参考文献：

[1]吴一全,朱兆达.图像处理中阈值选取方法30年(1962—1992)的进展(一) [J].数据采集与处理,1993,8(3):193- 201.

WU Yi-quan,ZHU Zhao-da.30 years (1962—1992) of the developments in threshold selection methods in image processing(1) [J].Journal of Data Acquisition & Processing,1993,8(3):193- 201.

[2]张煜东,吴乐南.基于二维Tsallis熵的改进 PCNN 图像分割 [J].东南大学学报(自然科学版),2008,38(4):579- 584.

ZHANG Yu-dong,WU Le-nan.Image segmentation based on 2D Tsallis entropy with improved pulse coupled neural networks [J].Journal of Southeast University(Natural Science Edition),2008,38(4):579- 584.

[3]魏武,姜莉,王新梅.基于最小类内方差的蛇形机器人多阈值分割 [J].华南理工大学学报(自然科学版),2013,41(5):9- 14.

WEI Wu,JIANG Li,WANG Xin-mei.Multi-threshold segmentation of snake-like robot based on minimum interclass variance [J].Journal of South China University of Technology(Natural Science Edition),2013,41(5):9- 14.

[4]KAPUR J N,SAHOO P K,WONG A K C.A new method for grey-level picture thresholding using the entropy of the histogram [J].Computer Vision,Graphics and Image Processing,1985,29(1):273- 285.

[5]ABUTALEB A S.Automatic thresholding of gray-level picture using two-dimensional entropies [J].Pattern Recognition,1989,47(1):22- 32.

[6]BARDERA A,BOADA I,FEIXAS M,et al.Image segmentation using excess entropy [J].Journal of Signal Processing Systems,2009,54(1/2/3):205- 214.

[7]CHEN W T,WEN C H,YANG C W.A fast two-dimensional entropic thresholding algorithm [J].Pattern Recognition,1994,27(7):885- 893.

[8]KOTAKOSKI J,KRASHENINNIKOV A V,KAISER U,et al.From point defects in grapheme to two-dimensional amorphous carbon [J].Physical Review Letters,2011,106(10):105505/1- 4.

[9]张毅军,吴雪菁,夏良正.二维图像阈值分割的快速递推算法 [J].模式识别与人工智能,1997,10(3):259- 264.

ZHANG Yi-jun,WU Xue-qing,XIA Liang-zheng.A fast recurring algorithm for two-dimensional entropic thresholding for image segmentation [J].Pattern Recognition and Artificial Intelligence,1997,10(3):259- 264.

[10]吴成茂,田小平,谭铁牛.二维熵阈值法的修改及其快速迭代法 [J].模式识别与人工智能,2010,23(1):127- 136.

WU Cheng-mao,TIAN Xiao-ping,TAN Tie-niu.Modification of two-dimensional entropic thresholding method and its fast iterative algorithm [J].Pattern Recognition and Artificial Intelligence,2010,23(1):127- 136.

[11]AGRAWAL S,PANDA R,BHUYAN S,et al.Tsallis entropy based optimal multilevel thresholding using cuckoo search algorithm [J].Swarm and Evolutionary Computation,2013,11:16- 30.

[12]SAHOO P K,ARORA G.Image thresholding using two-dimensional Tsallis-Havrda-Charvát entropy [J].Pattern Recognition Letters,2006,27(6):520- 528.

[13]WANG S,CHUNG F L.Note on the equivalence relationship between Renyi-entropy based and Tsallis-entropy based image thresholding [J].Pattern Recognition Letters,2005,26(14):2309- 2312.

[14]ARIMOTO S.Information theoretical consideration on estimation problems [J].Information and Control,1971,19(3):181- 194.

[15]卓问,曹治国,肖阳.基于二维Arimoto 熵的阈值分割方法 [J].模式识别与人工智能,2009,22(2):208- 213.ZHUO Wen,CAO Zhi-guo,XIAO Yang.Image thresholding based on two-dimensional Arimoto entropy [J].Pattern Recognition and Artificial Intelligence,2009,22(2):208- 213.

[16]张弘,范九伦.二维Arimoto熵直线型阈值分割法 [J].光子学报,2013,42(2):234- 240.

ZHANG Hong,FAN Jiu-lun.Two-dimensional Arimoto entropy linear-type threshold segmentation method [J].Acta Photonica Sinica,2013,42(2):234- 240.

[17]吴一全,曹鹏祥,王凯,等.二维Arimoto灰度熵阈值分割 [J].应用科学学报,2014,32(4):331- 340.

WU Yi-quan,CAO Peng-xiang,WANG Kai,et al.Two-dimensional Arimoto gray entropy thresholding [J].Journal of Applied Sciences,2014,32(4):331- 340.

收稿日期:2015- 06- 11

*基金项目:国家自然科学基金资助项目(61573183);江苏省制浆造纸科学与技术重点实验室开放基金资助项目(201313);农业部淡水渔业与种质资源利用重点实验室开放基金资助项目(KF201313);农业部东海海水健康养殖重点实验室基金资助项目(2013ESHML06);江苏高校优势学科建设工程项目(2012)

Foundation items: Supported by the National Natural Science Foundation of China(61573183),the Jiangsu Provincial Key Laboratory of Pulp and Paper Science and Technology(201313),the Key Laboratory of Freshwater Fisheries and Germplasm Resources Utilization(KF201313),the Key Laboratory of Healthy Magriculture for the East China Sea,Ministry of Agriculture(2013ESHML06) and the Priority Academic Program Development of Jiangsu Higher Education Institutions(2012)

作者简介:吴一全(1963-),男,博士,教授,博士生导师,主要从事图像处理与分析、目标检测与识别、智能信息处理研究.E-mail:nuaaimage@163.com

文章编号:1000- 565X(2016)05- 0048- 10

中图分类号：TP 391.41

doi：10.3969/j.issn.1000-565X.2016.05.008

Fast Iterative Algorithm for Image Threshold Segmentation Based on Two-Dimensional Arimoto Gray Entropy

WUYi-quan1,2,3,4ZHULi1WUShi-hua1

(1.College of Electronic and Information Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,Jiangsu,China;2. Jiangsu Provincial Key Laboratory of Pulp and Paper Science and Technology,Nanjing 210037,Jiangsu,China;3.Key Laboratory of Freshwater Fisheries and Germplasm Resources Utilization of the Ministry of Agriculture,Freshwater Fisheries Research Center,Chinese Academy of Fishery Sciences,Wuxi 214081,Jiangsu,China;4.Key Laboratory of Healthy Mariculture for the East China Sea,Ministry of Agriculture,Xiamen 361021,Fujian,China)

Abstract:As the existing Arimoto entropy-based thresholding methods only depend on the probability information from gray histogram and need to search the whole solution space to obtain the optimal threshold with low efficiency,a fast iterative algorithm for threshold segmentation on the basis of two-dimensional Arimoto gray entropy is proposed.Firstly,a fast iterative algorithm for threshold selection using one-dimensional Arimoto gray entropy is proposed.Secondly,by taking into consideration the gray level uniformity within the object cluster and the background cluster,a two-dimensional Arimoto gray entropy thresholding method on the basis of gray level-average gray level histogram is derived.Then,fast recursive formulae for intermediate variables are given.Finally,a fast ite-rative algorithm is proposed for threshold selection on the basis of two-dimensional Arimoto gray entropy,and the corresponding algorithmic formulae are derived,which helps reduce computation burden greatly.Experimental results show that the proposed algorithm is superior to five existing threshold segmentation algorithms because it runs more rapidly and is more effective in obtaining segmented images with complete objects,clear edges and rich details.

Key words:image segmentation; threshold selection;two-dimensional Arimoto gray entropy;fast iterative algorithm