基于改进RLM算法的横向控制过程的系统辨识*
2016-07-19石先城冯郁成陈克复
石先城 冯郁成 陈克复
(华南理工大学 制浆造纸国家重点实验室∥轻工与食品学院, 广东 广州 510640)
基于改进RLM算法的横向控制过程的系统辨识*
石先城冯郁成†陈克复
(华南理工大学 制浆造纸国家重点实验室∥轻工与食品学院, 广东 广州 510640)
摘要:横向控制过程测量数据的稀疏性以及模型的高维性、强耦合和不确定性使得系统模型难以辨识.为快速、准确地辨识系统模型,文中提出了一种改进的递推Levenberg-Marquart(RLM)算法.首先阐述了横向控制过程的二维参数化模型和辨识该模型的阶跃辨识方法,然后通过修正RLM算法的目标函数来改进RLM算法,并应用改进RLM算法实时递推辨识系统参数化模型的对位、稳态空间响应和动态响应.仿真实验与实际应用结果显示,该辨识方法不仅可以一致地辨识系统参数化模型的空间响应与动态响应,而且具有比传统RLM算法更快的收敛速度.
关键词:改进RLM算法;系统辨识;横向控制;造纸
在控制系统的设计中,系统辨识通常是最具挑战与耗时的环节.造纸过程的复杂性使得机理建模难以实现[1],同时往返式扫描架测量数据的稀疏性、横向控制过程的高维性与强相互作用、造纸过程的诸多不确定性,使得由输入输出数据准确地辨识横向控制系统变得尤其困难[2].横向控制系统模型包括空间响应和动态响应两部分.由于动态响应易于辨识,因此横向控制系统辨识的相关研究通常都是辨识系统的空间响应,包括对位与稳态空间响应[3- 5].
目前广泛应用于横向控制系统的辨识方法是:在多个横向控制点进行阶跃辨识,然后通过类最小二乘算法递推辨识参数化模型[3- 4,6- 7].由于待辨识模型的参数较多,二维横向控制模型被分解为空间响应模型与动态响应模型,然后分别辨识对位、稳态空间响应与动态响应,并在辨识过程中通过辨识数据来提高分解后模型的精度.这种辨识方法的缺点是辨识工作的复杂度高,分别辨识分解后的子模型不利于模型参数收敛于全局最优解.为减少辨识过程的复杂度,提升模型的辨识精度,文中提出了基于改进RLM算法的横向控制系统辨识方法,并通过仿真实验与实际结果的比较来验证该方法的可行性与有效性.
1横向控制系统模型与阶跃辨识
评价纸张质量的主要指标有定量、水分、厚度等,各指标可分为造纸机运行方向(纵向)和垂直于造纸机运行方向(横向)两部分,纸张质量横向控制的目标是使纸张横向质量保持均匀分布.纸张的横向质量是由一组或多组横向分区执行器控制,每组横向分区执行器包括30~200个执行器,各组执行器等间隔地分布在横向方向[8].纸张的横向质量由位于造纸机末端的安装在扫描架上往返移动的探头测量,探头移动一个周期可测量200~2 000个数据点.
纸张质量的横向控制过程如图1所示,纸张质量原始测量值经过数据预处理(包括滤波、纵向横向分离与下采样等)得到与横向执行器维数相同的横向测量值,该值与目标值比较后的残差输入至横向控制算法(包括横向滤波、动态补偿器与曲线平滑等),横向控制算法的输出为对应横向执行器的设定值,最后由横向执行器完成控制动作从而实现对纸张横向质量的控制[9].横向过程的复杂性使得机理建模难以实现,通常通过输入输出数据辨识系统模型并用于系统的控制中.
1.1横向控制系统模型
为使横向控制问题可控,通常假设过程的空间响应与动态响应可以分离,动态响应对于所有控制器都是一致的,而且如果不考虑纸边引起的变化,则可以认为横向控制过程是空间无关的,即每个横向控制器的空间响应是相同的[10- 11].因此,横向控制过程的输入输出模型[8]可表示为
y(t)=Gh(z-1)u(t)+d(t)
(1)
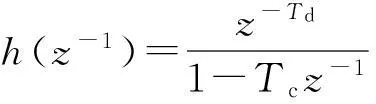
(2)
式中:y(t)∈Rm,u(t)∈Rn,d(t)∈Rm,分别为横向质量的测量值、控制输入和噪声;G∈Rm×n,为稳态空间响应,通常为带状对称对角矩阵(Toeplitz 矩阵);h(z-1)为动态响应的一阶惯性延时传递函数;Td、Tc分别为纯滞后时间和惯性延时,Td包括固定延时与传输延时,传输延时由控制器到扫描架的距离和纸机的车速共同决定,固定延时通常为设备本身的反应时间.文献[1]已经证明,单个横向控制器的空间响应可以用一组正交的基本函数的扩展式来表示,这样既可以减小模型识别所需的参数,又可以对系统的闭环稳定性产生积极的效果.稳态空间响应矩阵G中一个完整的列以gj(x)表示,即第j个横向控制器对纸张横向质量的影响,文献[7]对此给出了通用的表示:
(3)
式中,κj、αj、βj、ωj分别为增益、衰减因子、发散因子和宽度,单个横向控制器对纸张质量测量点两侧ωj宽度内的纸张质量有影响且影响的增益为κj,衰减因子表示gj两侧负旁瓣的衰减程度,发散因子表示gj中两个波峰间的距离(如板纸机),当发散因子为0时gj只有一个波峰(如标准形式、高斯形式).gj的形状如图2所示.
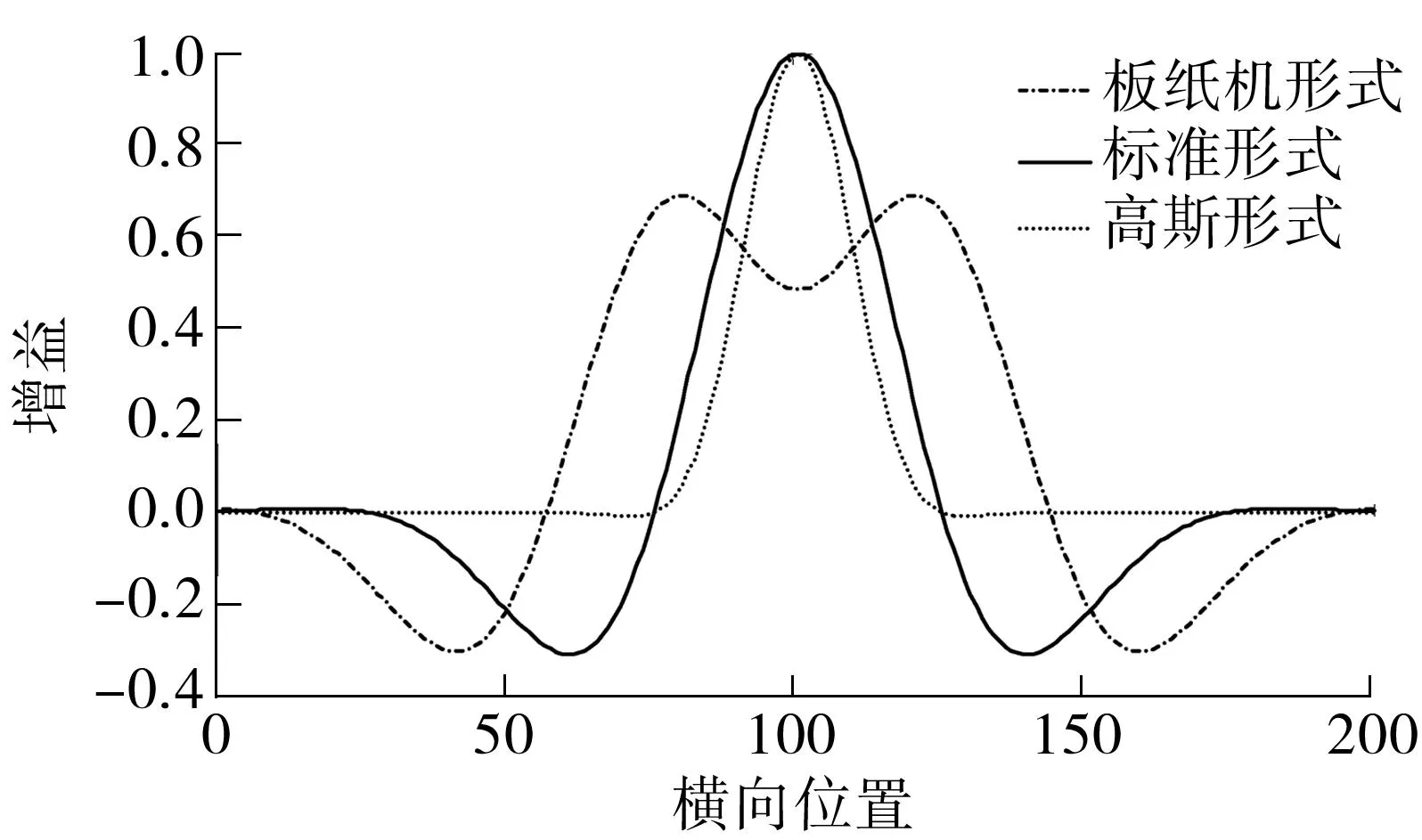
图2 横向控制系统的稳态空间响应
Fig.2Steady-state spatial response of cross-directional control system
对于稀释水模型,当βj=0,αj=7时,gj两侧的负旁瓣基本消失,则只需识别gj(x)中的κj与ωj,因此,式(3)可以简化为
(4)
由于横向过程的数据测量点与控制点数巨大,要实现横向控制,需要横向执行器与对应测量点间彼此对应,称为对位.文献[12- 13]指出,只要对位偏差超过1/3的执行器宽度,就会引起横向控制质量的严重下降.考虑线性对位模型:
cj=c0+(xj-0.5x*)(1-s0)
(5)
式中,cj为第j个横向控制器的响应中心,xj为第j个横向控制器的位置,x*为横向控制器组的整体宽度(通常为浆流出唇板的宽度减去两侧的切边宽度),c0为偏移常量,s0为纸张的一致收缩率,s0=(x*-c*)/x*,x*为切边后的横向执行器宽度,c*为成纸的宽度.则横向控制过程的通用传递函数模型可以表示为
G(t)=Gh(t)=[g1,g2,…,gn]h(t)=
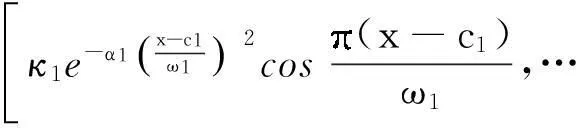
(6)
1.2阶跃辨识
纸机横向控制系统的阶跃辨识应在纸机稳定后进行,尤其是纸张的纵向质量需要尽可能地保持稳定,否则纵向质量的波动会对横向控制过程的辨识造成影响.纸机横向控制系统的阶跃响应辨识是通过在多个互不干扰的横向控制点进行阶跃实验并将辨识模型拓展至全部横向控制点,通常包括以下步骤[7]:
(1)对横向控制过程的参数进行预估计,如根据纸机的车速、控制器与扫描架之间的距离估计动态响应的时滞,根据纸张的定量、上浆浓度、稀释水浓度预估计稀释水响应的增益,根据纸机车速估计稀释水影响宽度;
(2)设置阶跃辨识参数,根据预估的过程参数设置阶跃点的位置与幅度、阶跃实验的持续时间;
(3)同时在横向方向进行多个阶跃测试,并收集纸张质量的测量数据;
(4)根据输入输出数据离线或在线地辨识对位、空间响应和动态响应;
(5)根据实际情况对模型参数进行微量调整以使模型匹配得更好.
在横向控制系统的阶跃辨识中,选取执行器的原则包括:①阶跃点的个数尽可能多,以便尽可能多地辨识更多阶跃点的响应模型;②阶跃点间的距离应确保相邻阶跃点的响应模型互不干扰,以使输入输出数据可辨识;③阶跃点的位置与阶跃方向应有助于改善当前纸张的质量;④总阶跃量应保持在0附近,以减少对纵向质量的干扰.
2改进的RLM算法
横向模型的辨识过程实际上是一个非线性优化问题,可以通过梯度法、高速牛顿法、拟牛顿法、LM算法进行求解,LM算法因具有高斯-牛顿法与梯度下降法的优点而受到了广泛的关注[14].批训练LM算法只能在收集完所有的数据后才能开始,不适用于需要实时、在线处理数据的自适应控制和需要实时优化的领域.RLM算法可以实时地辨识系统模型、检测辨识实验的优劣和观测辨识结果.
定义RLM算法[15]的目标函数为

(7)
式中:e(,W)为残差向量;W为待优化参数向量;(0<≤1)为遗忘因子,其表示历史数据的相关性以相应的遗忘速度递减.式(7)的遗忘因子之和
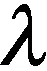
(8)
消除遗忘因子累加和的影响,将式(7)改写为

(9)
对W求一阶导数,得

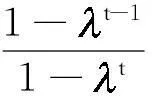
(10)
式中,J(t,W)=∂e(t,W)/∂W,为雅可比矩阵.
再对W求二阶导数,得

(11)
当W接近理想值时,∂2e(t,W)/∂W2≈0,整理式(11)得
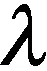
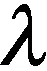
(12)
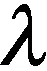
(13)
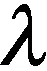

(14)
基于目标函数(7),RLM算法为
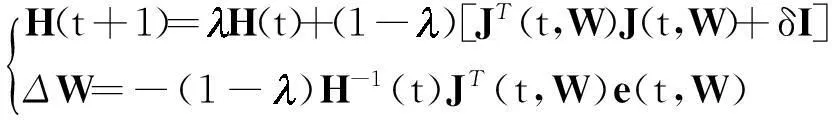
(15)
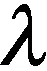
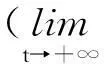
当优化问题的参数较多、输出较少时,直接对H(t)求逆的计算量为O(d3)(d为参数维数),应用矩阵求逆引理[15]可以将计算量减小到O(d2).但文中的横向过程辨识问题的输出数大于待辨识参数个数,应用矩阵求逆引理会增加计算量,故文中采用Cholesky分解来求取ΔW:
[R,RT]=chol(H(t))
(16)
(17)
式中,chol( )表示Cholesky分解,R为分解后的上三角矩阵,“”表示矩阵左除.
控制参数δ对LM算法至关重要,δ过大会使LM算法在梯度下降方向优化而导致收敛速度慢,δ过小则可能导致Hessian矩阵不可逆而使LM算法无法继续进行.RLM算法由于应用了矩阵求逆引理,故只有每次迭代之后才对δ进行更新[15],文中对δ的迭代方法进行了调整.
对式(9)进行Taylor展开:
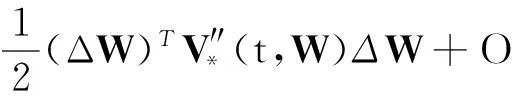
(18)
只考虑式(18)的前两项,则性能函数V*(t,W)在t时刻的预测减少量为
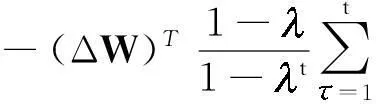

(19)
性能函数在每次迭代的实际减少量为
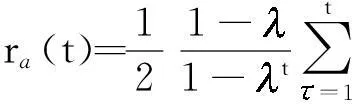
eT(,W+ΔW)e(,W+ΔW)]=
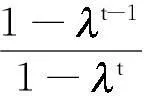
eT(t,W+ΔW)e(t,W+ΔW)]
(20)
则改进RLM算法的控制参数δ的调整策略为
(21)
式中:δ(t)的初值选择范围为[10-4,10-1];δmax、δmin分别为δ的最大值、最小值;ζ的取值范围为(0,0.5),通常取0.25;κIn、κDe的取值范围为(1,10).
3应用改进的RLM算法辨识横向过程
目前广泛采用的横向过程辨识方法[6- 7]可独立地迭代辨识空间响应与时间响应模型,但这种方法不利于系统模型参数的全局收敛.为此,文中采用改进的RLM算法一致地辨识横向过程.横向控制系统的参数化模型中待辨识参数为W=[Tc,Td,κ1,ω1,c1,…,κn,ωn,cn];c1,c2,…,cn的初值可以由线性模型给定,其他参数初值则根据经验或相关文献给定.系统辨识的目标是使得模型辨识残差保持最小:


(22)
式中,e(t,P)=[e1(t,P),…,em(t,P)]T,ei(t,P)=yi-G(i,∶)h(t)ub,G(i,∶)为矩阵G的第i个行向量,ub为阶跃输入.
以上求模型参数的问题实际上是非线性二次优化问题,文中采用改进的RLM算法来求解横向模型的参数辨识问题.设阶跃输入点为b1,b2,…,bk,则雅可比矩阵(∂e(t,W)/∂W)为
(23)
(24)
(25)

(26)
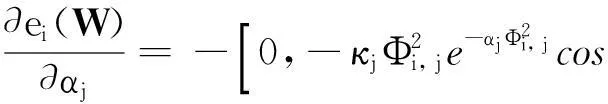
(27)

(28)


(29)
式中,Φi, j=(i-cj)/ωj,各梯度由通用横向过程模型(9)求出.由式(24)、(25)可知,在t≤Td时梯度为0,h(t)=0,则在这个时间范围内无法正常进行系统辨识,这里将Td初始估计值置为较小的正值,以便辨识过程能顺利进行.
给定横向过程待辨识参数的初值W0,在基础扫描次数后,给定系统阶跃输入ub,t时刻的Wt由改进RLM算法实时优化求解得到,再通过Wt预测系统下一时刻的输出并实时观测辨识模型与系统实际输出的匹配度,最后根据辨识结果与实际需求微调系统模型的辨识参数.
4实验结果与分析
4.1仿真实验
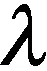
仿真实验结果如图3所示.在图3(a)中,沿着扫描次数轴的不同凸出波形代表阶跃输入的对应输出,凸出波形的波峰为阶跃输入执行器的对位点.波形沿扫描次数轴为执行器的动态响应,垂直于扫描次数轴为执行器的空间响应.从图3(b)可知,辨识模型的初始给定值与实际值有一定的偏差,尤其是增益与对位,在前几步的模型输出中,未完全辨识的波形峰值与完全辨识的波形峰值明显不在同一测量点,经过若干步的迭代辨识后,模型输出与实际输出保持一致,模型的辨识结果见表1.由表中可知,改进RLM算法可以准确地辨识横向过程的对位和稳态横向响应参数κ、ω,辨识误差均值分别为4.25%、3.08%、2.6%,辨识的动态响应结果为Tc=28.854s、Td=38.389s,辨识误差分别为7.99%和3.70%,远小于可接受的20%[9],辨识效果十分理想.
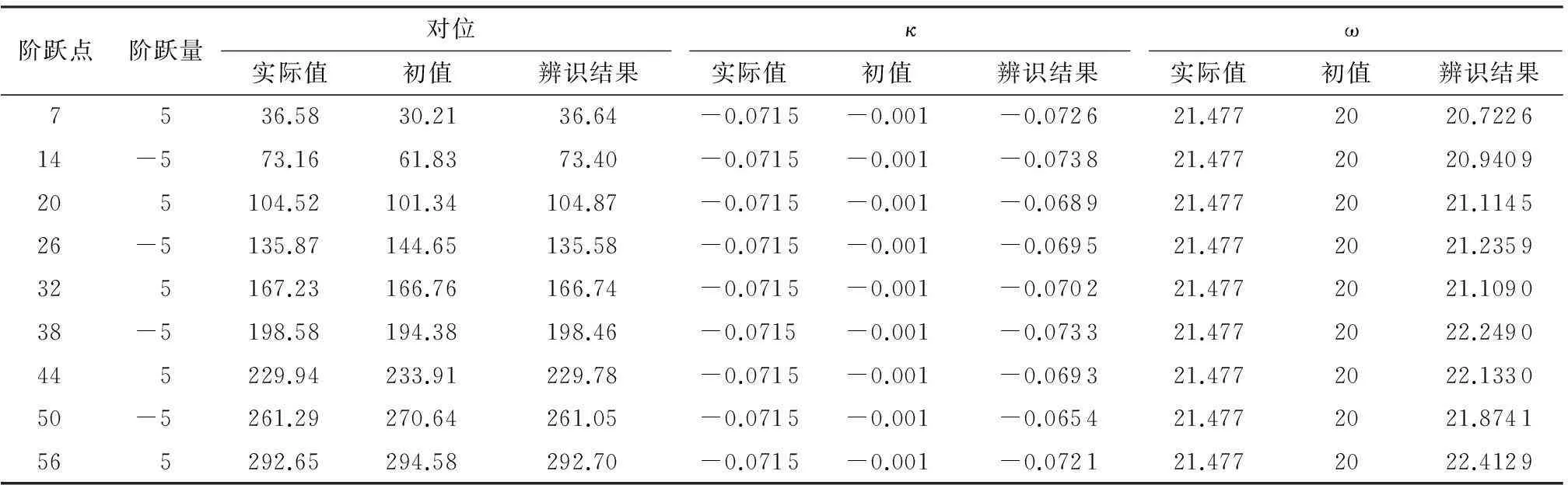
表1 仿真实验的辨识结果
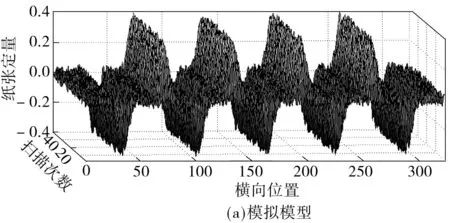

图3 仿真实验的横向辨识过程
Fig.3Cross-directionalidentificationprocedureofsimulations
4.2现场实验
现场实验数据通过在某纸机中进行阶跃实验获得,其中的阶跃量因横向过程有较大的扰动而给定较大的值.由于得到的输入、输出数据会受到不同程度噪声的影响,故文中采用低通滤波器对横向数据进行滤波去噪,并通过指数滤波尽可能地减小纵向扰动对横向测量数据的影响[17].该纸机纸张质量控制系统的横向质量测量点数为282、宽为24.30mm,稀释水分区个数为94、宽为74.5mm,左、右水针切边均为37.25mm,左、右纸边的波动范围分别为1.287±0.039测量区、278.356±0.059测量区,由式(8)计算得到整幅纸张的收缩率为2.825%.生产纸张的定量为105g/m2,纸机车速为863.3m/min,从控制器到扫描架的传输距离为150m,扫描架测量周期为31s,则传输延时为10.43s.
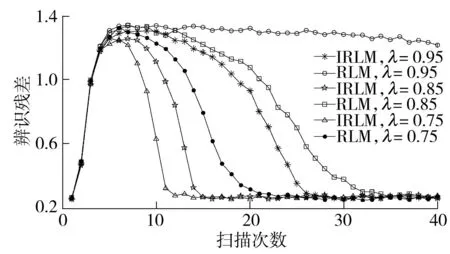
图4 仿真实验中横向控制系统辨识残差
Fig.4Identificationresidualofcross-directionalcontrolsysteminsimulations

表2 现场实验的辨识结果


图5 现场实验的横向辨识过程
Fig.5Cross-directionalidentificationprocedureofpracticaltests
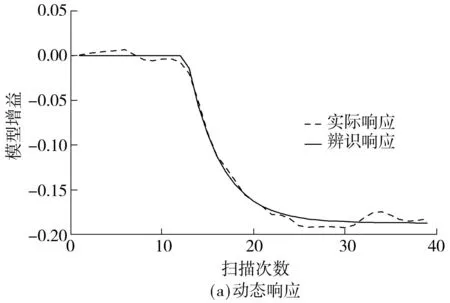
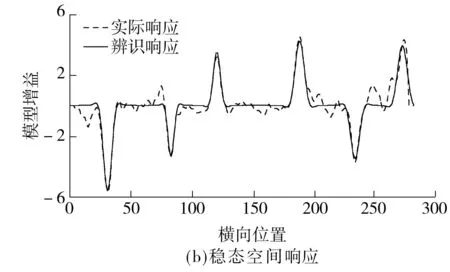
图6 动态响应和稳态空间响应的辨识结果
Fig.6Identificationresultsofthedynamicresponseandthesteady-statespatialresponse
系统模型辨识完成,且横向过程运行稳定后,由于造纸过程的复杂性,可能会出现模型失配的情况.工业过程通常都有较大的干扰,在设计控制器时需要考虑可能的模型不确定性,即保证控制器的鲁棒性,实际中应用的横向控制器通常为鲁棒控制器,允许系统模型有最大为30%的模型不确定性[1,9],当模型失配严重到影响正常生产时,需要重新辨识模型以使系统稳定运行.
5结论
为快速、准确地递推辨识横向控制系统,文中提出了一种改进的RLM算法.与基于最小二乘辨识方法将二维横向控制系统辨识问题分解为多个一维模型辨识的方法不同,文中基于改进RLM算法的辨识方法可以直接辨识二维横向控制系统,降低了辨识工作的复杂性,减少辨识过程的迭代步骤,同时提升了辨识结果的准确性.改进RLM算法在辨识系统参数化模型时具有更好的收敛速度,适用于实时与在线辨识.仿真实验与现场实验结果验证了所提方法的可行性与有效性.
参考文献:
[1]FEATHERSTONEAP,VANANTWERPJG,BRAATZRD.Identificationandcontrolofsheetandfilmprocesses[M].London:Springer,2000.
[2]VANANTWERPJG,FEATHERSTONEAP,BRAATZRD,etal.Cross-directionalcontrolofsheetandfilmproce-sses[J].Automatica,2007,43(2):191- 211.
[3]HEAVENEM.Applicationofsystemsidentificationtopapermachinemodeldevelopmentandsimulation[J].PulpandPaperCanada,1996,97(4):49- 54.
[4]CHENSC,SUBBARAYANR.Identificationtemporalandspatialresponseofcrossmachineactuatorsforsheetfor-mingprocesses[J].IEEProceedings:ControlTheoryandApplications,2002,149(5):3082- 3086.
[5]SAFFERDR,DOYLEFJ.Closed-loopidentificationwithMPCforanindustrialscaleCD-controlproblem[J].IEEProceedings:ControlTheoryandApplications,2002,149(5):448- 456.
[6]GORINEVSKYDM,HEAVENEM.Performance-optimizedappliedidentificationofseparabledistributed-parameterprocesses[J].IEEETransactionsonAutomaticControl,2001,46(10):1584- 1589.[7]GORINEVSKYDM,GHEORGHEC.Identificationtoolforcross-directionalprocesses[J].IEEETransactionsonControlSystemTechnology,2003,11(5):629- 640.[8]HAZNEDARB,ARKUNY.SingleandmultiplepropertyCDcontrolofsheetformingprocessviareducedorderinfinitehorizonMPCalgorithm[J].JournalofProcessControl,2002,12(1):175- 192.
[9]STEWARTGE,GORINEVSKYDM,DUMOUTGA.Feedbackcontrollerdesignforaspatiallydistributedsystem:thepapermachineproblem[J].IEEETransactionsonControlSystemsTechnology,2003,11(5):612- 628.[10]DUNCANSR,BRYANTGF.Thespatialbandwidthofcross-directionalcontrolsystemsforwebprocesses[J].Automatica,1997,33(2):139- 153.
[11]DUNCANSR,ALLWOODJM,HEATHWP.Dynamicmodelingofcross-directionalactuators:implicationsforcontrol[J].IEEETransactionsonControlSystemsTechnology,2000,8(4):667- 675.
[12]NUYANS,SHAKESPEAREJ,FUC.RobustnessandstabilityinCDcontrol[J].PulpandPaperCanada,2002,103(5):120- 123.[13]TAYLORAR,DUNCANSR.Detectingmismappingincross-directionalcontrolsystems[J].IEEETransactionsonControlSystemsTechnology,2010,18(4):962- 968.
[14]NOCEDALJ,WRIGHTSJ.Numericaloptimization[M].Berlin:Springer,2006.[15]NGIALS,SJOBERGJ.EfficienttrainingofneuralnetsfornonlinearadaptivefilteringusingarecursiveLevenberg-Marquardtalgorithm[J].IEEETransactionsonSignalProcessing,2000,48(7):1915- 1927.
[16]GOLUBGH,VANLOANCF.Matrixcomputations[M].Maryland:JohnsHopkinsUniversityPress,1996.[17]AMMARME,DUMONTGA.Identificationofpapermachinescross-directionalmodelsinclosed-loop[C]∥ProceedingsofInternationalConferenceonModeling,Identi-ficationandControl.Cairo:IEEE,2013:3- 9.
收稿日期:2015- 02- 25
*基金项目:国家水体污染控制与治理科技重大专项(2014ZX07213001);广州市科技计划项目(201504010013)
Foundation item:Supported by the National Water Pollution Control and Treatment Science and Technology Major Project(2014ZX07213001)
作者简介:石先城(1988-),男,博士生,主要从事先进控制、人工智能与系统集成研究.E-mail:sxc7101@126.com †通信作者: 冯郁成(1971-),男,高级工程师,主要从事高速造纸机关键技术与装备研究.E-mail:fengyc@scut.edu.cn
文章编号:1000- 565X(2016)05- 0058- 08
中图分类号:TP 273
doi:10.3969/j.issn.1000-565X.2016.05.009
SystemIdentificationofCross-DirectionalControlProcessesBasedonImprovedRLMAlgorithm
SHI Xian-chengFENG Yu-chengCHEN Ke-fu
(StateKeyLaboratoryofPulpandPaperEngineering∥SchoolofLightIndustryandFoodSciences,SouthChinaUniversityofTechnology,Guangzhou510640,Guangdong,China)
Abstract:In cross-directional(CD) control processes,the system model is difficult to identify due to the sparse measurement data as well as the model's high dimensionality,strong coupling and uncertainty.In order to identify the system model rapidly and accurately,an improved approach on the basis of the recursive Levenberg-Marquardt(RLM) algorithm is proposed.Firstly,the two-dimension parameterized model and step identification method of CD control processes are described.Secondly,the objective function of RLM algorithm is modified and an improved RLM algorithm is presented,which is then applied to the real-time and recursive identification of the mapping,steady-state spatial response and dynamic response of the parameterized model of CD control processes.The results of both simulation and practical application show that the proposed identification method can not only identify the spatial and dynamic responses of CD control processes simultaneously but also converge more rapidly than the traditional RLM algorithm.
Key words:improved RLM algorithm;system identification;cross-directional control;papermaking
