级联自适应陷波器设计及不同步脉冲计数补偿*

刘桂雄　万勇　黄坚　潘云飞

(1.华南理工大学 机械与汽车工程学院, 广东 广州 510640; 2.广州能源检测研究院, 广东 广州 510170)



级联自适应陷波器设计及不同步脉冲计数补偿*

刘桂雄1万勇2黄坚1潘云飞2

(1.华南理工大学 机械与汽车工程学院, 广东 广州 510640; 2.广州能源检测研究院, 广东 广州 510170)

摘要:为减小计数误差及实现多路不同步异频脉冲信号的高精度测量,设计了一款可实时估计周期脉冲信号相位的级联自适应陷波器(CANF).首先在前端固定一自适应因子为0的Liu型自适应陷波器(LANF),然后将LANF的输出作为Mojiri型自适应陷波器(MANF)的输入,再利用MANF的估计频率实时调整LANF,最后在流量计标准装置中实现CANF的相位实时估计,并对两路不同步脉冲信号进行精度补偿.仿真实验结果表明CANF的计数误差小于±0.047个脉冲,工程应用实验结果表明CANF的计数误差小于±0.045个脉冲,说明了文中通过实时计算信号相位进行计数补偿的方法能有效提高脉冲计数检定精度和多路并行检定的实用性.

关键词：陷波器;级联;自适应算法;不同步脉冲;误差补偿

将测量量转化为计数脉冲是工业生产、实时监测、自动化控制等领域广泛使用的技术手段,但一次检定多个频率、相位不一致的脉冲信号时,难以应用同步计数法来消除计数误差.文献[1- 2]针对异频不同步信号提出了一种相位补偿方法,但只适合测量两路不同步信号的计数值,并且需要使用高频信号发生器HP8664A产生辅助测量信号.使用时间数字转换器(TDC)也是提高脉冲计数精度的有效方法,但脉冲计数测量对象通常是低频脉冲信号,对时间精度要求不高(微秒级)[3- 6];TDC应用于微秒级时间间隔测量时存在电路规模大、动态范围有限及易受干扰脉冲影响等问题.由于周期脉冲信号可通过傅里叶级数分解为不同频率正弦信号的线性叠加,滤除周期信号3次谐波及以上分量,就可以在获取同频基波信号的同时滤除随机干扰.笔者在前期研究的流量标准装置中嵌入基于陷波滤波器的脉冲补偿算法,计数精度提高了0.06个[7],而自适应陷波滤波器(ANF)[8]可自动使其陷波频率跟随输入信号频率变化、抑制噪声,并提取信号幅值、频率、相位.

为减小计数误差,有效提高计数精度,文中在通用数据采集卡基础上,应用ANF技术,设计了一款可实时估计周期脉冲信号相位的级联自适应陷波器(CANF),并提出了一种多路不同步脉冲计数补偿方法.

1CANF设计

Regalia[9]在局部平均方法、自适应律基础上设计了第一类型ANF,但其受正弦信号幅值、频率耦合的影响,频率估计暂态响应速度受幅值大小的影响明显.Liu等[10]根据缓慢积分流形原理设计了一种收敛速度几乎不受幅值影响的全局收敛归一化ANF(LANF),但LANF仅能处理单正弦输入信号,不适合测试计量领域的周期脉冲信号.Mojiri等[11- 12]采用局部平均方法、Lasalle不变集理论设计了一种固定自适应增益为γ的ANF(MANF);MANF能很好地处理受谐波干扰的正弦输入信号,近年来获得了广泛的工程应用[13- 16],但均未讨论输入为周期方波的情况.为探讨MANF处理周期脉冲信号的性能,设周期脉冲幅值为A、初相位为φ、角频率为ω,则根据傅里叶级数展开式可得到信号在任意t时刻的测量值f:

(1)

(2)

(3)

对于周期输入信号,动态系统(2)、(3)具有唯一的周期轨道Γ1:

Γ1=(x1,x2,θ)=

若不考虑式(3)的自适应率,则式(2)对应的传递函数为

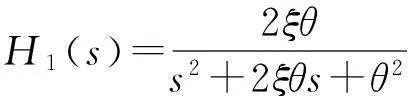
(4)

(5)

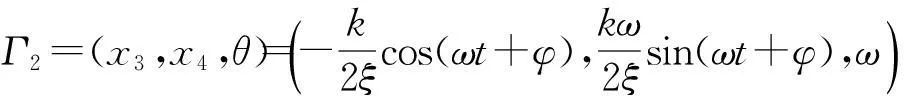
由Γ2可以看出,x4与输入基波信号同频、同相.按缓慢积分流形原理设置γ=0,则LANF为

(6)

式(6)实际上为一共振器,如果采用级联形式固定θ于MANF频率估计值,则对于频率为θ的周期脉冲信号,动态系统(4)、(5)可滤除该信号的3次谐波及以上分量.将x3作为MANF的输入,可以解决在奇次谐波叠加干扰下MANF状态变量x1、x2偏离周期轨道Γ1及收敛速度慢等问题,图1为级联自适应陷波器CANF的原理框图.

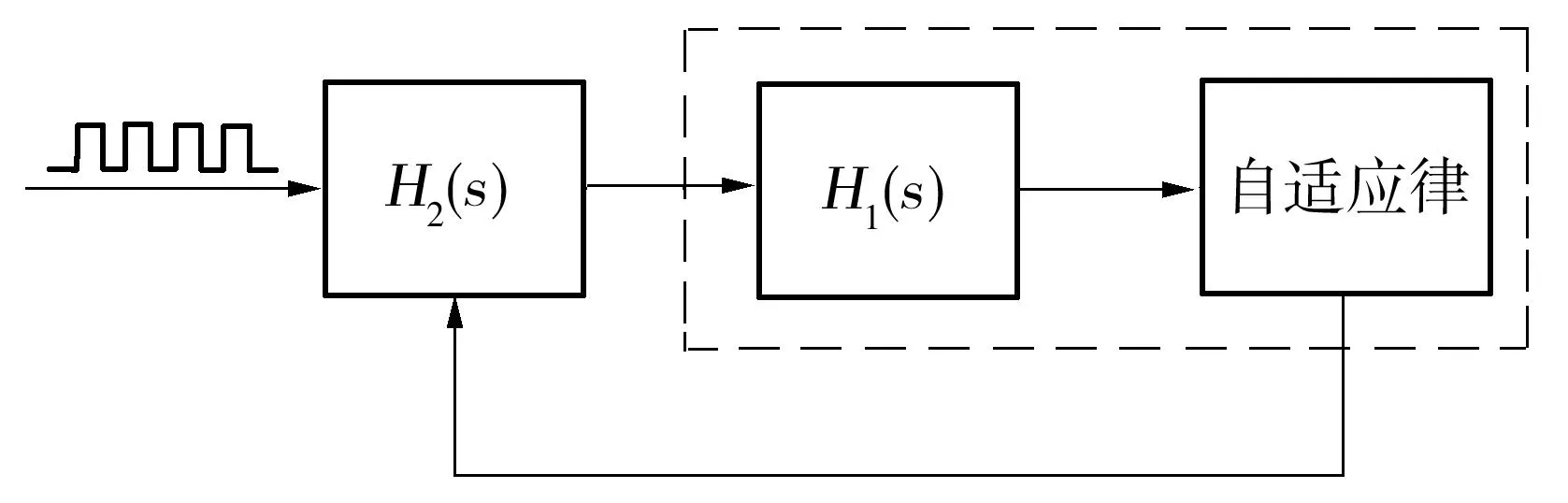
图1　CANF的原理框图

(7)

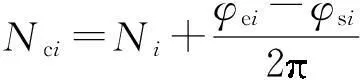
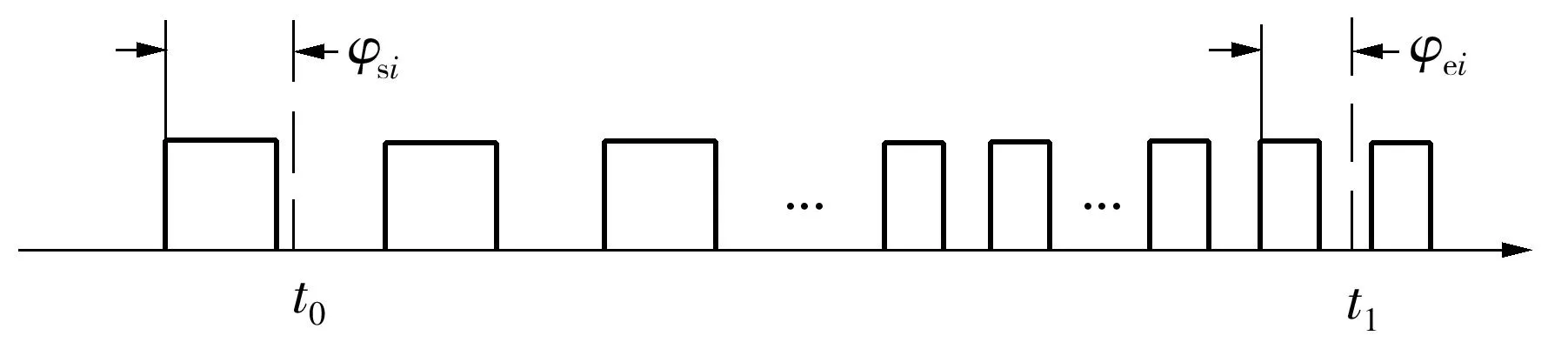
图2　脉冲计数补偿原理图

2仿真实验及工程应用实验

2.1仿真实验

对MANF和CANF分别输入相同的脉冲信号:幅值A=10 V、频率f=10 Hz、初相φ0=0 rad,设置ξ=0.7,γ=1,角频率预估初值θ0=100 rad/s,则MANF和CANF状态变量x1、x2的稳态响应曲线、角频率估计曲线分别如图3、4所示.

从图3(a)可以看出,在奇次谐波叠加干扰下,x1和x2偏离轨道Γ1,算法很难根据x1和x2估计相位.从图3(b)可知,在第25秒处，角频率估计值仍在偏离真实值4.5 rad/s处震荡,收敛时间较长,说明MANF不能很好地处理周期脉冲输入信号.从图4(a)可知,对于周期脉冲信号输入,x1和x2的正弦度好,与预定周期轨道Γ1相符.从图4(b)可以看出,角频率估计值θ在第3秒处进入真实值附近小幅震荡.图3、4说明,对于同频周期脉冲输入信号,相同参数的CANF较MANF大大缩短了收敛时间,状态变量x1和x2更加接近其预定周期轨道,并在很大程度上提高了频率估计的准确度,其根本原因在于CANF前置的H2(s)滤除了大部分谐波信号.

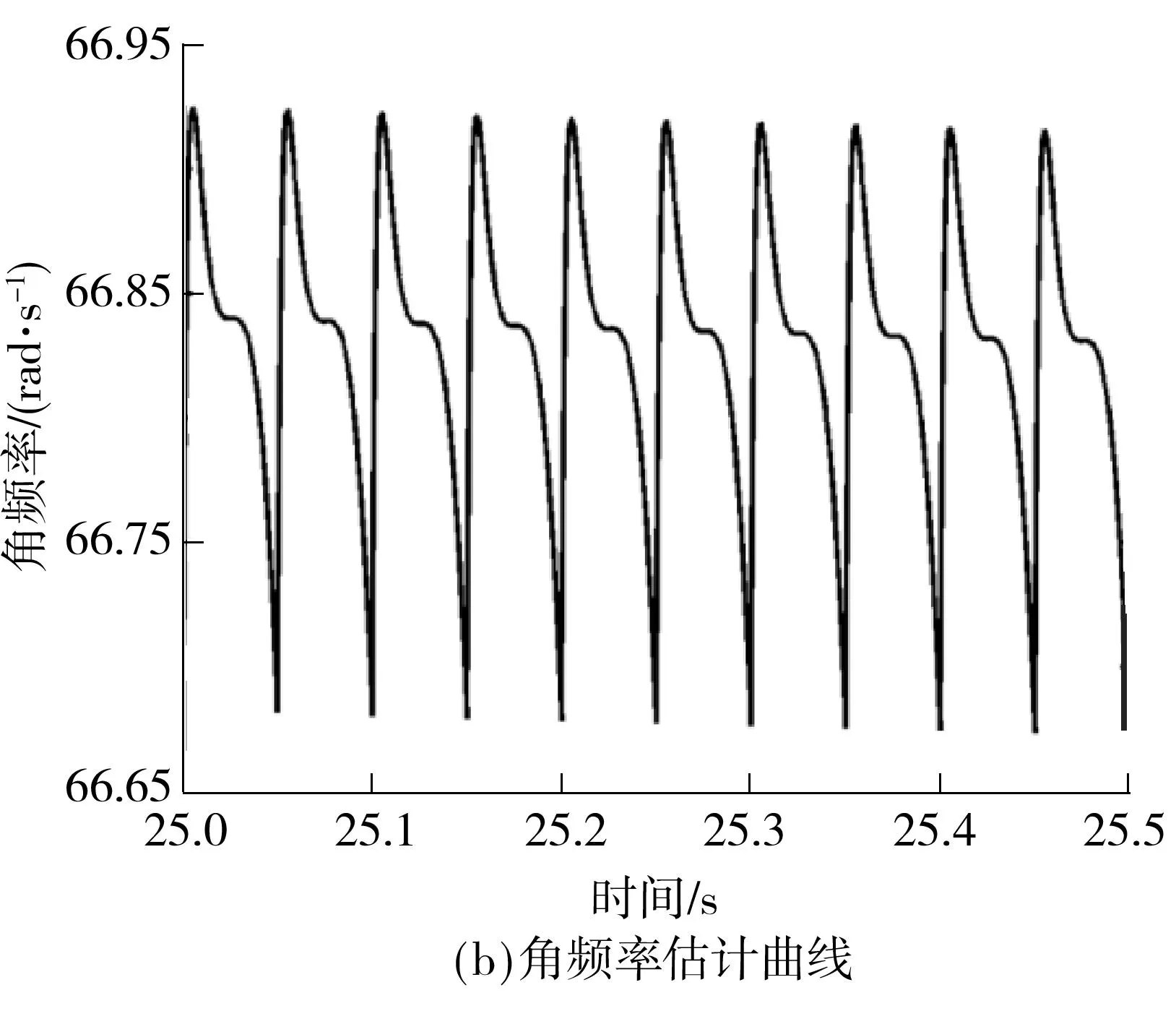
图3　MANF的状态变量稳态曲线和角频率估计曲线

Fig.3Stability curves of status variables and estimated angular frequency curve of MANF

2.2计数补偿效果实验

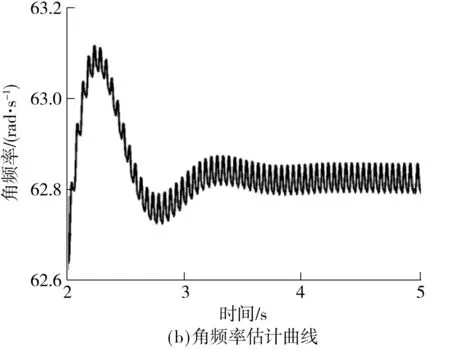
图4　CANF的状态变量稳态曲线和角频率估计曲线

Fig.4Stability curves of status variables and estimated angular frequency curve of CANF

表1为对3路输入脉冲信号进行计数补偿的实验数据,测量时长分别为1.0、2.5、5.0 s.可以看出,上升沿检测法计算所得脉冲个数在很多情况下均存在±1的计数误差,但经过CANF实时估计相位进行计数补偿后,计数误差小于±0.047个脉冲.

图5为CANF状态变量x3、x4的80 Hz脉冲响应曲线,由于单通道实际采样频率仅为2.5 kHz,80 Hz输入信号造成了状态变量的正弦度较差,但实验曲线的幅值、频率及相位均符合其稳态周期轨道Γ2,故根据x3、x4计算的补偿脉冲计数值具有较高的精度.

2.3工程应用实验

在广州能源检测研究院DN20双台位流量计标准装置上进行工程应用实验.图6为双台位流量计标准装置机理图、实物图.在流量计校准过程中,流量波动导致脉冲信号频率在某一范围内波动,不能以“频率×时间”方式获得脉冲计数值.图7为补偿算法效果验证示意图,实验中标准流量计获得原始脉冲信号,输出至偶数分频器(分频比为100),并通过研华工控机610L上计数装置对分频前、后信号与换向信号进行上升沿计数(换向信号整周期截取),采用阿尔泰PCI8602型数据采集卡采集分频后信号进行脉冲计数补偿.在2.5、5.0、10.0 m3/h流量下计数精度补偿算法效果验证实验结果见表2.从表中可以看出,在不同流量下,上升沿检测法计算所得脉冲个数存在±1的计数误差,经补偿后计数误差小于±0.045个脉冲,极大地提升了计数精度.

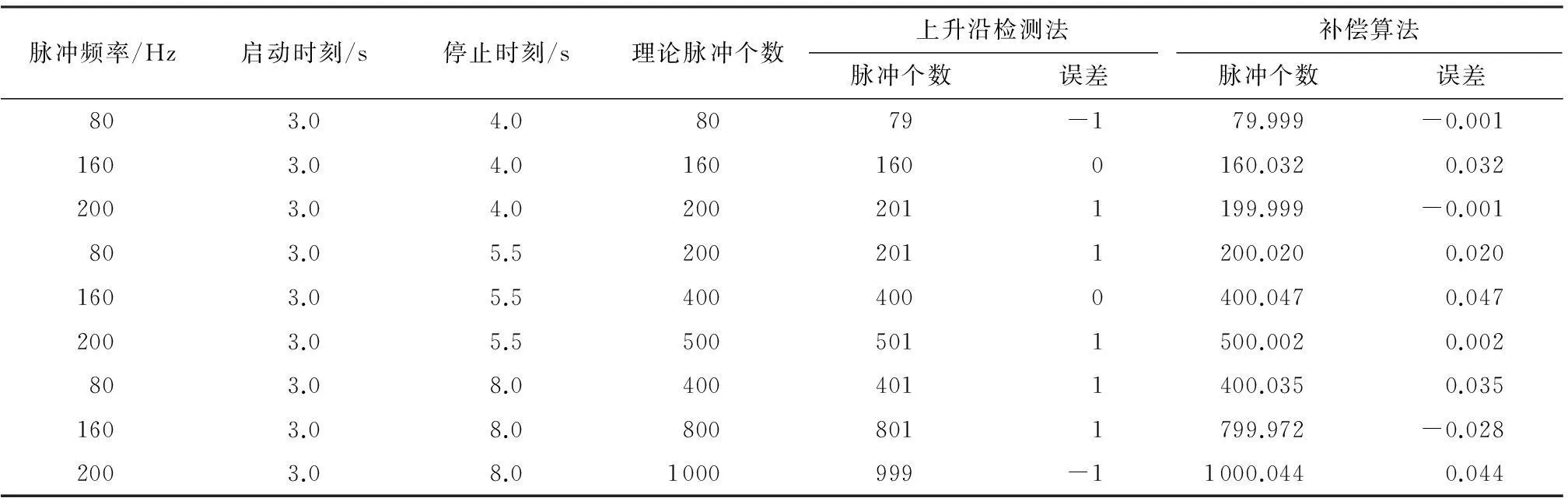
表1　在采样频率10 kHz下的计数精度补偿实验结果

图5　CANF状态变量的80 Hz脉冲响应曲线

图6　双台位流量计标准装置的机理图和实物图

Fig.6Mechanism and photo of two-station flowmeter calibration equipment

图7　计数精度补偿算法效果验证示意图

Fig.7Schematic diagram of effect validation for counting precision compensation algorithm

表2计数精度补偿算法效果验证实验结果

Table 2Experimental results of effect validation for counting precision compensation algorithm

流速/(m3·h)分频前脉冲计数分频后脉冲计数计数误差真值不补偿补偿后不补偿补偿后2.55.010.020052200.52200200.516-0.52-0.00420152201.52202201.4880.48-0.03220169201.69201201.670-0.69-0.02020149201.49202201.5010.510.01120164201.64202202.6850.360.04520345203.45204203.4660.550.01620252202.52203202.5540.480.03420456204.56204204.572-0.560.01220460204.60205204.5870.40-0.013

3结论

文中根据缓慢积分流形原理设计了一款级联自适应陷波器,并将其应用于多路不同步脉冲计数补偿.仿真与实验结果表明:①该级联自适应陷波器的谐波干扰抑制能力好,可限制无限次奇次谐波叠加引起的干扰,很好地解决了LANF仅能处理单正弦输入信号、MANF不能处理周期脉冲信号的问题;②该级联陷波器的频率、相位估计准确性在3组不同步计数补偿实验中的计数误差小于±0.047个脉冲;③在双台位流量计标准装置上实现的工程应用实验中的计数误差小于±0.045个脉冲.这种通过实时计算信号相位进行计数补偿的方法能有效地提高脉冲计数检定精度和多路并行检定的实用性.

参考文献：

[1]DU Baoqiang,WANG Yanfeng,ZHOU Wei,et al.Ultra-resolution phase comparison method combining phase synchronous detection and common frequency source [J].Measurement,2013,46(1):374- 377.

[2]杜保强,左艳迪,周渭,等.优于皮秒分辨率的特高频率测量方法 [J].北京邮电大学学报,2013,36(6):84- 88.

DU Bao-qiang,ZUO Yan-di,ZHOU Wei,et al.Extra-high frequency measurement for picoseconds resolution [J].Journal of Beijing University of Posts and Telecommunications,2013,36(6):84- 88.

[3]JANSSON J P,MANTYNIEMI A,KOSTAMOVAARA J.Synchronization in a multilevel CMOS time-to-digital converter [J].IEEE Transactions on Circuits and Systems I:Regular Papers,2009,56(8):1622- 1634.

[4]CHEN C C,LIN S H,HWANG C S.An area-efficient CMOS time-to-digital converter based on a pulse-shrin-king scheme [J].IEEE Transactions on Circuits and Systems II:Express Briefs,2014,61(3):163- 167.

[5]冯智辉,邓飞其,刘文辉.一类二次型离散系统的有限时间稳定与镇定 [J].华南理工大学学报(自然科学版),2015,43(1):9- 14.

FENG Zhi-hui,DENG Fei-qi,LIU Wen-hui.Finite-time stability and stabilization for a class of quadratic discrete-time systems [J].Journal of South China University of Technology(Natural Science Edition),2015,43(1):9- 14.

[6]CHUNG M H,LIU W S,CHOU H P.Time amplification using closed-loop differential amplifier [C]∥Proceedings of 2012 IEEE Nuclear Science Symposium and Medical Imaging Conference.Anaheim:IEEE,2012:789- 792.

[7]廖晓文,刘桂雄,潘云飞.一种高精度多路脉冲计数补偿方法 [J].电子测量与仪器学报,2015,29(7):1074- 1079.

LIAO Xiao-wen,LIU Gui-xiong,PAN Yun-fei.Compensation method for high precision multi-channel pulse coun-ting [J].Journal of Electronic Measurement and Instrumentation,2015,29(7):1074- 1079.

[8]万勇,潘云飞,杨茹.基于级联自适应陷波器的多路不同步脉冲计数补偿方法:201510366719.1 [P].2015- 09- 22．

[9]REGALIA P A.An improved lattice-based adaptive IIR notch filter [J].IEEE Transactions on Signal Processing,1991,39(9):2124- 2128.

[10]LIU Hsu,ORTEGA R,DAMM G.A globally convergent frequency estimator [J].IEEE Transactions on Automa-tic Control,1999,44(4):698- 713.

[11]MOJIRI M,BAKHSHAI A R.An adaptive notch filter for frequency estimation of a periodic signal [J].IEEE Transactions on Automatic Control,2004,49(2):314- 318.

[12]MOJIRI M,KARIMI-GHARTEMANI M,BAKHSHAI A.Time-domain signal analysis using adaptive notch filter [J].IEEE Transactions on Signal Processing,2007,55(1):85- 93.

[13]PYRKIN A A,BOBTSOV A A,NIKIFOROV V O,et al.Output control approach for delayed linear systems with adaptive rejection of multiharmonic disturbance [C]∥Proceedings of the 19th IFAC World Congress.Cape Town:IFAC,2014:7579- 7584.

[14]FEDELE G,FERRISE A.A frequency-locked-loop filter for biased multi-sinusoidal estimation [J].IEEE Tran-sactions on Signal Processing,2014,62(5):1125- 1134.

[15]KETABI A,FARSHADNIA M,MALEKPOUR M,et al.A new control strategy for active power line conditioner (APLC) using adaptive notch filter [J].International Journal of Electrical Power & Energy Systems,2013,47(5):31- 40.

[16]PYRKIN A,SMYSHLYAEV A,BEKIARIS-LIBERIS N,et al.Output control algorithm for unstable plant with input delay and cancellation of unknown biased harmonic disturbance [J].Time Delay Systems,2010,9(1):39- 44.

收稿日期:2015- 10- 08

*基金项目:国家重大科学仪器设备开发专项(2013YQ230575);广州市技监局科技计划项目(2015KJ35)

Foundation item:Supported by the National Important Scientific Instrument Exploring Foundation of China(2013YQ230575)

作者简介:刘桂雄(1968-),男,教授,博士生导师,主要从事先进传感与仪器研究.E-mail:megxliu@scut.edu.cn

文章编号:1000- 565X(2016)05- 0084- 06

中图分类号：TH- 3

doi：10.3969/j.issn.1000-565X.2016.05.013

Design of Cascade-Connection Adaptive Notch Filter and Counting Compensation of Asynchronous Pulses

LIUGui-xiong1WANYong2HUANGJian1PANYun-fei2

(1.School of Mechanical and Automotive Engineering,South China University of Technology,Guangzhou 510640,Guangdong,China;2.Guangzhou Institute of Energy Detection,Guangzhou 510170,Guangdong,China)

Abstract:In order to reduce counting error and implement high-accuracy measurement of multi-channel asynchronous impulse signals with different frequencies,a cascade-connection adaptive notch filter(CANF) for real-time phase estimation is proposed.In CANF,firstly,an ANF designed by Liu(LANF) with an adaptive factor of 0 is set in the front of ANF,and the output of LANF is used as the input of an ANF designed by Mojiri(MANF).Secondly, the estimated frequency of MANF is used to adjust the frequency of LANF in real time.Then,CANF is applied to a multi-station flowmeter calibration equipment and is used to calculate the real-time phase of two channels of asynchronous impulse signal.Finally,simulation and practical application of CANF are carried out,with the corresponding counting errors being less than ±0.047 and ±0.045,respectively,which means that the counting error compensation via real-time phase calculation effectively improves the counting accuracy of asynchronous pulses and the practicability of multi-channel parallel calibration.

Key words:notch filters;cascade connections;adaptive algorithms;asynchronous pulse;error compensation