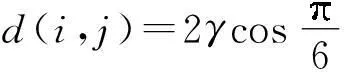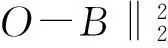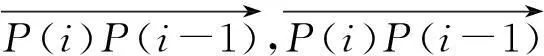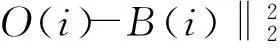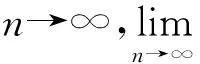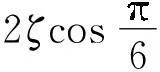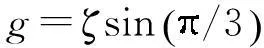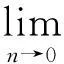基于布尔搜索的空间目标分布最小包围盒规划*
2016-07-19卫星韩江洪
卫星 韩江洪
(合肥工业大学 计算机与信息学院∥教育部安全关键工业测控工程研究中心,安徽 合肥 230009)
基于布尔搜索的空间目标分布最小包围盒规划*
卫星韩江洪
(合肥工业大学 计算机与信息学院∥教育部安全关键工业测控工程研究中心,安徽 合肥 230009)
摘要:为了降低对平面内无源目标进行定位产生的搜索代价,研究了确定覆盖所有随机部署的无线传感器网络节点的最小包围盒问题.首先提出基于布尔搜索的无线传感器网络节点最小包围盒规划方法,运用深度优先策略,使锚节点不断逼近目标节点的实际位置;然后根据前述算法完成时的锚节点坐标,设计了坐标最大-最小值规划算法以构造最小覆盖面积包围盒.最后通过仿真和算法分析得出,所提策略计算复杂度低于遍历方式的最小包围圆、包围盒算法,且能更准确地估计出覆盖面积最小的包围盒.
关键词:无线定位;最小包围盒;覆盖圆;凸壳规划
在一些事故场景中,存在大量的目标物体需要被定位.例如,飞机的残骸碎片、战后遗弃的地雷、甚至是放射性的核泄漏物等.与通常的目标定位不同,它们大多是随机散落在一片空间内,都是无源的,无法通过测量目标与参照物之间的距离估计其位置坐标[1].对于类似的被动目标定位,划分出一块面积尽可能小的搜索范围,直接决定了目标定位所需要花费的代价[2].
目前,以位置指纹匹配法为代表的诸多定位方法,均以目标位置与场景特征形成的一对一映射作为定位的先验条件[3- 5],这些方法都需要事先划分覆盖所有目标的规则形状.如此,最小覆盖面的划分问题就转化为包含全部目标的最小包围形状的规划问题[6- 7].在计算几何领域,研究最小包围形状的算法很多,经典的包括最小包围圆规划和最小包围盒规划[8- 9].其中,最小包围盒是一种覆盖面积最小的规则矩形,其规划算法的复杂度小于最小包围圆,广泛用于碰撞检测、模具分形设计与模式识别[10].
在目标坐标未知情况下,根据深度优先搜索策略,文中提出了布尔搜索的锚节点位置规划算法,通过局部覆盖目标分布的外围区域,使得锚节点深度遍历过程中,不断迭代逼近外围的目标.根据迭代完成时的锚节点坐标,设计了坐标最大-最小值规划算法,构造了覆盖面积接近最小的包围盒.
1问题描述
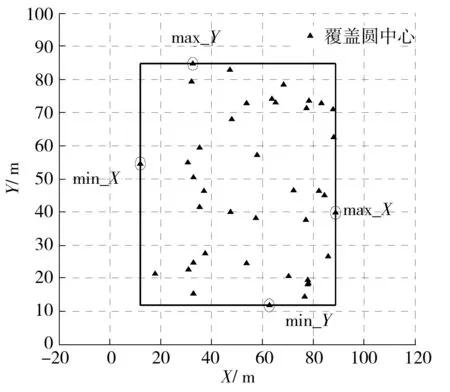
给定长宽均为L的矩形区域Ω,其4个顶点的直角坐标分别为O(0,0)、B(0,L)、C(L,L)和D(L,0).n个目标物构成的平面点集S分布在Ω内,S={s1,s2,…,sn}.∀si∈S的坐标值以均匀分布的随机方式产生,si=(Lθi,1,Lθi,2),θi,1,θi,2~N(0,1),表示极角.n≥3时,根据S构成的凸壳顶点BCH(S′)为一个凸多边形G,G的顶点均来自S.令P为包围S的最小凸多边形,即不存在凸多边形P′,使得P⊃P′⊃S成立.
(a)轴向矩形包围盒

(b)定向矩形包围盒
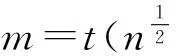
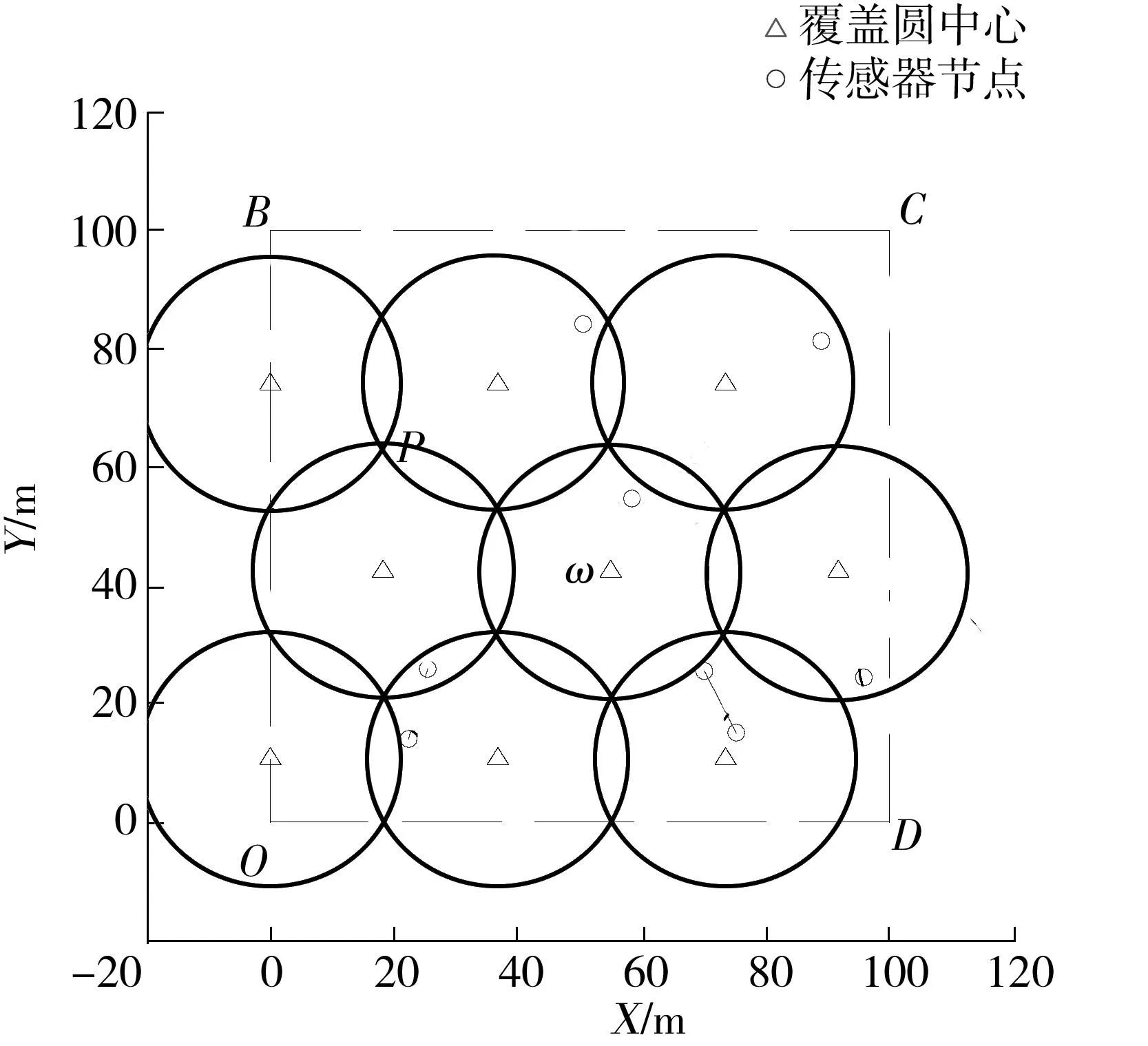
2布尔搜索的锚节点部署
通过锚节点的信号接收范围,构建相应的覆盖圆,实现Ω局部区域的覆盖,完成S凸壳顶点BCH(S)的搜索.
定义1锚节点i部署在a(i)点,其信号接收半径为r(i),则i形成一个覆盖圆,记作[a(i),r(i)].
如果锚节点i在覆盖圆[a(i),r(i)]内收到信号,则向Sink发送信息,表示至少存在一个目标δ(i)∈S,使得[a(i),r(i)]将其包含.由于发送的信息被锚节点i量化为1比特的局部消息M(i),

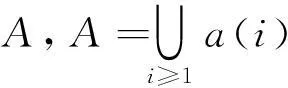

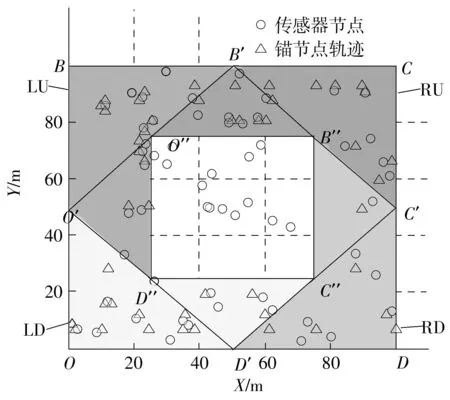
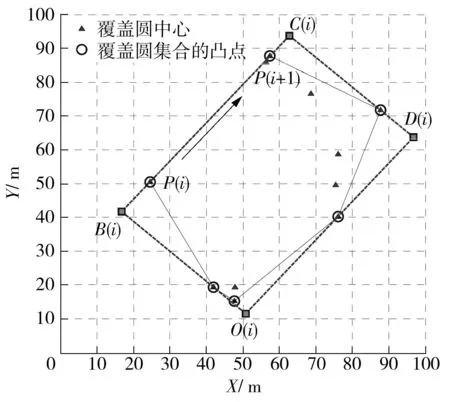
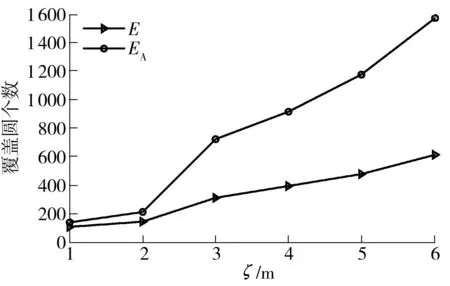
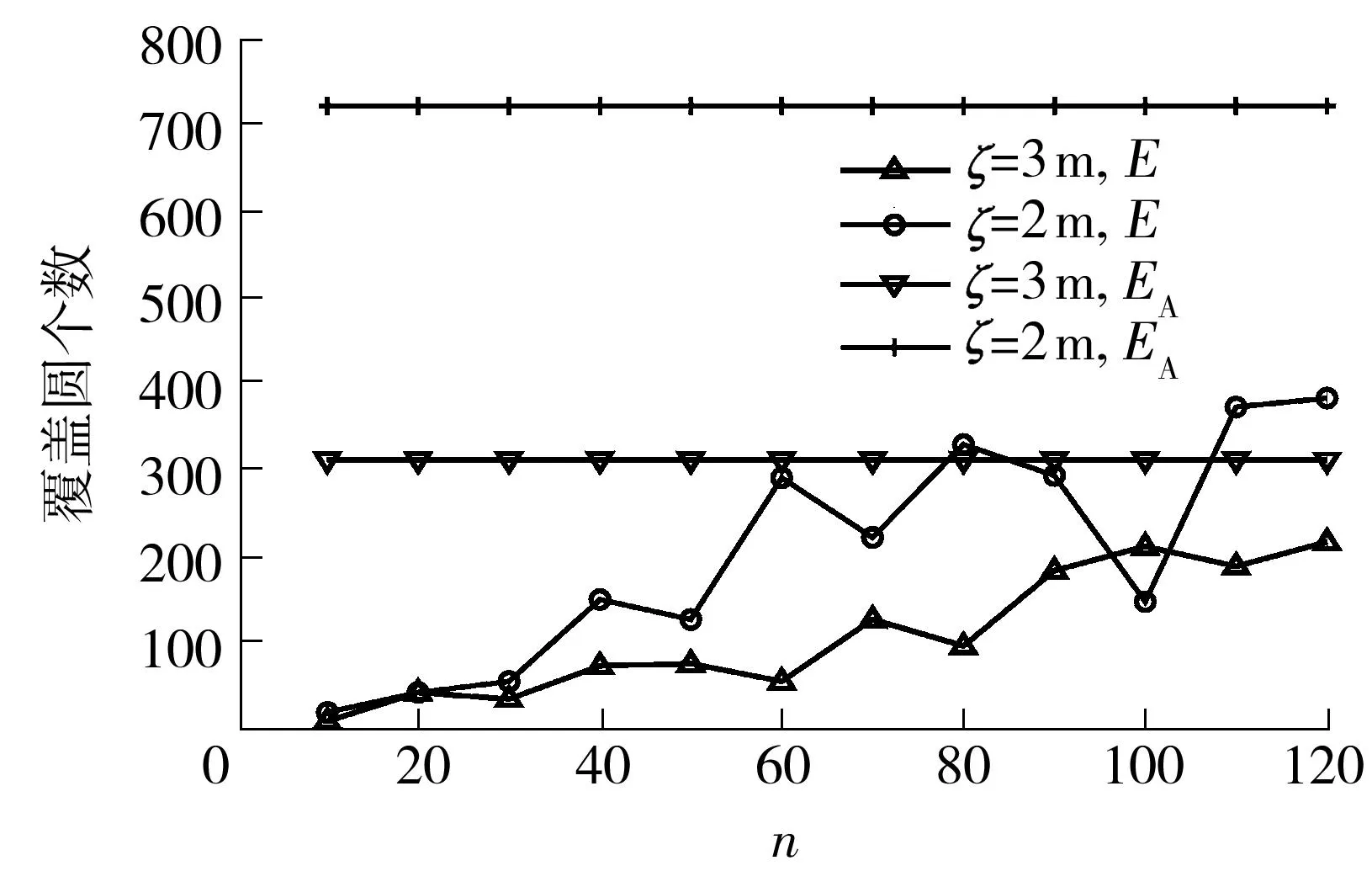
定义3设覆盖圆a(i)和a(j)的中心距离为d(i,j),d(i,j)=‖a(i)-a(j)‖2,如果d(i,j) 算法1A←Anchor array(ω,d,P) 输出:A为规划的覆盖圆心坐标集合; ω为当前的覆盖圆心坐标; 图2 覆盖圆的局部覆盖 输入:d为ω与相邻覆盖圆心的欧式距离; P为凸多边形,P⊂Ω; 过程:① 若(ω,d)没有节点,转向③; ② A←cover_search( ω,γ,γ/[2cos(/6)]) ;\子覆盖圆规划 ④ 依次设v={α,β,T,J,Q,K},如果v位于P内,A←v; ⑤A←Anchor_array(v,d,P). 函数A←cover_search(ω,r,ρ) 输出:A为覆盖圆ω内规划的子覆盖圆心坐标 ω为覆盖圆的中心; 输入:r为ω的半径; ρ为子覆盖圆ωi+1的半径; ② 依次设ωi+1={α,β,T,J,Q,K},如果满足(ωi+1,ρ)存在节点,(ωi+1,ρ)⊄(ω,r),ρ>ζ,则A←ωi+1; ④A←cover_search(ωi+1,r,ρ). 为4个方向的出发点. 图3 局部覆盖情况下搜寻外围节点过程 Fig.3Node searching process under the circumstance of partial coverage 3坐标最大-最小值的最小包围盒规划 A′的个数为m,存在a∈A′,以及∀s∉S,满足‖a-s‖2≤ζ.首先,运用Graham算法从A′提取构成凸壳边界BCH(A′)的顶点集合Π,凸壳顶点个数为η.根据Π的X坐标的最小值min_X和最大值max_X,以及Y坐标的最小值min_Y和最大值max_Y,建立顶点O(min_X,min_Y)、B(min_X,max_Y)、C(max_X,max_Y)和D(max_X,min_Y),顺序连接上述4个顶点,可以建立面积最小的轴向包围盒ΣZ,如图4所示.ΣZ的面积为S(ΣZ), |max_X-min_X||max_Y-min_Y| (1) 图4 最小覆盖面积的轴向包围盒 图5 最小覆盖面积的定向包围盒 为S的最小包围盒,i∈[1,2,…,η],其算法如下. 算法2V←maxmin_coordinate(A′) 输出:最小包围盒Σ的顶点坐标V; 输入:A′覆盖圆的中心集合; 过程:①P←graham(A′),采用Graham算法求出A′中的凸壳边界顶点P; ② head←P(i),rear←P(i+1);rear在Ψ内的极角为θ(i); ③ 将Ψ的中心平移至head,再逆时针偏转θ(i),得到新的坐标系Ψ(i); ④ 计算P在Ψ(i)的直角坐标P(i); ⑤ 从P(i)提取max_X、min_X、max_Y和max_Y; ⑥ 提取Ψ(i)下的定向包围矩形Σ(i)的4个顶点,以顺时针方向:O(i)=(min_X,min_Y),B(i)=(min_X,max_Y),C(i)=(max_X,max_Y),D(i)=(max_X,min_Y); 4算法效率分析 文中通过比较覆盖圆全覆盖方法与算法1的效率,证明算法1的覆盖圆部署代价小于一般性的方法.算法效率是指在给定的相同边长区域Ω和相同阈值ζ的情况下,满足每个目标至少被一个覆盖圆布尔覆盖时,算法输出的最大覆盖圆个数.其中,算法1输出的覆盖圆半径γ是变长的,在布尔搜索过程中,随着搜索深度的增加,γ逐渐减小,如定理1所示. 而一般的全覆盖方法是不再规划子覆盖圆,所有输出的覆盖圆半径均为阈值ζ. 由定理2可知,全覆盖方法在搜索部署过程中,始终是以半径r满足小于等于ζ的覆盖圆实现Ω的全覆盖,该方法是固定尺度的搜索,与算法1的变尺度搜索策略相比,算法的时间复杂度低,且锚节点的感知半径是固定的,输出的覆盖圆个数必然大于算法1.因此,如果锚节点的感知范围在线性可调的情况下,算法1的算法效率明显优于全覆盖方法. 5仿真实验与分析 采用Matlab 2013b作为仿真实验平台,正方形区域Ω给定的长宽均为100 m.根据算法1,对图3所示区域进行布尔搜索的锚节点部署.设定初始时的锚节点覆盖圆半径r=14.142 m,阈值ζ为2 m和3 m时,分别进行12组仿真.每组仿真随机生成的节点数为n,算法1产生的包含节点的覆盖圆个数为E,全覆盖方法包含节点的覆盖圆个数为EA.算法2规划的最小定向包围盒面积为ΣD,最小轴向包围盒面积为ΣZ. 图6为固定节点个数n=100时覆盖圆个数随ζ的变化曲线,可见,阈值ζ越大,锚节点覆盖圆个数E和EA越大.由图7可知,随着节点个数增加,覆盖面积在初始阶段呈现折线增长的趋势,节点个数增加到一定程度后,覆盖面积的变化规律不明显.由图8可知:EA始终大于E;阈值ζ相同条件下,EA没有随着n的增加而递增,而E则随着n的增加而增大.这也验证了定理1所描述的,算法1的代价与n存在线性相关.同时,n存在一个门限值ε,Ω面积为100 m2时,根据定理1和定理2计算得出:ζ=2 m时,ε=371;ζ=3 m时,ε=249;当n>ε时,算法1的代价将超过全覆盖方法.因此,节点密度较小时,适合运用算法1的搜索策略. 图6 覆盖圆个数随阈值的变化 Fig.6Changes of the number of cover circles with the increase of threshold 图7 覆盖面积随节点个数的变化 图8 覆盖圆个数随节点个数的变化 Fig.8Changes of the number of cover circles with the increase of nodes 根据分析遗漏的节点个数R可知,n较小时,ΣD遗漏的节点数较多;随着n的增加,使得用于规划ΣD的覆盖圆个数E也增加,如果覆盖圆分布的广泛,则遗漏的节点数会下降.根据图9数据分析得出,R由覆盖圆分布的范围决定.ΣD的面积越大,覆盖圆的分布范围也就越大,而E也就越高.如图10所示,n=40时,算法2规划的最小定向包围盒为ΣD,最小轴向包围盒为ΣZ.根据前述结果可知,ΣD在任何情况下的面积均小于或等于ΣZ.由于覆盖圆的中心并非完全与S节点位置重合,所以ΣD之外仍存在少量的节点. 图9 遗漏节点数随节点个数的变化 Fig.9Changes of the number of missed node with the increase of nodes 图10 40个传感节点规模的最小包围盒 6结论 根据深度优先搜索策略,实现了锚节点覆盖圆对节点平面的局部覆盖.随着搜索深度的增加,不断减小锚节点布尔感知范围,使得产生的覆盖圆中心点持续逼近节点的实际位置.仿真实验结果表明,基于DFS的布尔搜索得出的覆盖圆中心坐标,使得构建的最小包围盒仅将少量的节点排除在外.通过变换经纬度坐标系,根据提取的坐标最大、最小值所获得的包围盒面积均小于坐标系变换前的最小包围盒面积.同时,在相同低密度节点分布的情况下,基于DFS的布尔搜索代价小于以往的全覆盖方法. 参考文献: [1]SHRIVASTAVA N,MUDUMBAI R,MADHOW U,et al.Target tracking with binary proximity sensors [J].ACM Transactions on Sensor Networks,2009,5(4):1- 33. [2]郭庆胜,冯代鹏,刘远刚.一种解算空间几何对象的最小外接矩形算法 [J].武汉大学学报· 信息科学,2014,39(2):177- 180. GUO Qing-sheng,FENG Dai-peng,LIU Yuan-gang,et.al.An algorithm for computing the smallest-area enclosing rectangle of spatial geometric object(s) [J].Geomatics and Information Science of Wuhan University,2014,39(2):177- 180. [3]ZHAO C,HEINZELMAN W B.Searching strategy for multi-target discovery in wireless networks [C]∥Proceedings of 4th Workshop on Applications and Services in Wireless Networks.Boston:IEEE,2004:1- 10. [4]WANG H,SEN S,ELGOHARY A,et al.No need to war-drive:unsupervised indoor localization [C]∥Proceedings of the 10th International Conference on Mobile Systems,Application,and Services.New York:ACM,2012:197- 210. [5]马燕,袁蔚林,陈秀万,等.基于WiFi和GPS组合定位算法的无缝定位方法研究 [J].地理与地理信息科学,2013,29(3):6- 16. MA Yan,YUAN Wei-lin,CHEN Xiu-wan,et al.A seamless positioning method research based on wireless local area network (WiFi) and GPS [J].Geography and Geo-Information Science,2013,29(3):6- 16. [6]王小平,罗军,沈昌祥.无线传感器网络定位理论和算法 [J].计算机研究与发展,2011,48(3):353- 363. WANG Xiao-ping,LUO Jun,SHEN Chang-xiang.Theory and algorithms on localization in wireless sensor networks [J].Journal of Computer Research and Development,2011,48(3):353- 363. [7]WEI W,VIKRAM S,BANG W,et al.Coverage for target localization in wireless sensor networks [J].IEEE Tran-sactions on Wireless Communication,2008,7(2):667- 676. [8]GAVSHIN Y,KRUUSMAA M.Improving area coverage by reversible object pushing [C]∥Proceedings of 15th International Conference on Advanced Robotices.Tallinn:IEEE, 2011:415- 420. [9]JIANG X,FAN Y B,WEI S,et al.An algorithm of weighted Monte Carlo localization based on smallest enclosing circle [C]∥Proceedings of 2011 International Confe-rence on and 4th International Conference on Cyber,Phy-sical and Social Computing.Dalian:IEEE, 2011:157- 161.[10]陈华.确定任意形状物体最小包围盒的一种方法 [J].工程图学学报,2010,31(3):353- 363. CHEN Hua.A method to generate the minimum bounding boxes for shape-arbitrary objects [J].Journal of Engineering Graphics,2010,31(3):353- 363. [11]ULLRICH T,FUNFZIG C,FELLNER D W.Two diffe-rent views on collision detection [J].IEEE Potentials,2007,26(1):26- 30. [12]LI G B,TANG J.A new K-NN query algorithm based on the clustering and sorting of minimum bounding rectangle [C]∥ Proceedings of 2nd International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC).Nanjing:IEEE,2010:196- 199. [13]周培德.计算几何:算法设计与分析 [M].3版.北京:清华大学出版社,2008:214- 216. 责任编辑:牛晓光 收稿日期:2015- 01- 14 *基金项目:国家自然科学基金资助项目(61370088);国家国际科技合作专项项目(2014DFB10060);安徽省自然科学基金资助项目(1408085MKL80) Foundation items: Supported by the National Natural Science Foundation of China(61370088),the International S & T Cooperation Program of China(2014DFB10060)and the Natural Science Foundation of Anhui Province(1408085MKL80) 作者简介:卫星(1980-),男,副教授,主要从事物联网工程、离散事件动态系统研究.E-mail:weixing72510@163.com 文章编号:1000- 565X(2016)05- 0144- 07 中图分类号:TP 393.0 doi:10.3969/j.issn.1000-565X.2016.05.022 Smallest Enclosing Rectangle Planning for Spatial Target Distribution on the Basis of Boolean Search WEIXingHANJiang-hong (School of Computer and Information∥Engineering Research Center of Safety Critical Industrial Measurement and Control Technology of the Ministry of Education, Hefei University of Technology, Hefei 230009, Anhui, China) Abstract:In order to save the searching cost of passive target location in two-dimension planes, a smallest enclosing rectangle problem for randomly-deployed WSN (Wireless Sensor Network) nodes is investigated. Firstly, a smallest enclosing rectangle planning method for WSN nodes, which makes anchors continuously approach target nodes with the depth-first searching strategy, is proposed on the basis of Boolean search. Then, a coordinate max-min algorithm is put forward to compute the minimum enclosing rectangle according to aforementioned anchors’ location. The results of both simulation and algorithm analysis show that the proposed strategy possesses less computation complexity than such searching strategies as traversal methods for smallest enclosing rectangle and circle, and helps obtain the enclosing rectangle with minimum area more precisely. Key words:wireless localization; smallest enclosing rectangle; cover circle; convex planning