一种多粒度语言的多属性群决策方法

张小刚,张　亮,王端民,翟楠楠

(空军工程大学 装备管理与安全工程学院，陕西 西安　710051)



一种多粒度语言的多属性群决策方法

张小刚,张亮,王端民,翟楠楠

(空军工程大学 装备管理与安全工程学院，陕西 西安710051)

摘要:针对多粒度语言的多属性群决策问题,文章提出了一种基于二元语义及改进多准则妥协解排序(VIKOR)的群决策方法。首先将不同粒度语言的偏好信息一致化为由基本语言评价集表示的相同粒度二元语义信息;在专家属性未知且方案属性不完全的情形下,分别运用有序加权平均算子(2-tuple ordered weighted averaging,T-OWA)与相对熵从客观角度计算权重;为进一步挖掘决策数据的内在规律,引入灰色关联系数改进评判矩阵,结合该矩阵利用VIKOR方法刻画最优方案。算例结果验证了该方法的有效性和可行性。

关键词:多属性群决策;二元语义;灰色关联矩阵;相对熵;改进多准则妥协解排序

0引言

多粒度语言的多属性群决策问题是决策者采用不同粒度语言信息数目(简称粒度)表示的语言评价集测评有限备选方案,按照某种规则集结为决策群体的一致或妥协的群体偏好序[1]。这类问题广泛地存在于建设投资、项目管理[2]等方面。对不同粒度信息的一致化,文献[3]采用二元语义[4-5]表示不同粒度语言,并用一致化方法处理不同粒度专家偏好信息,有效地解决了不同粒度信息一致化问题。文献[6-7]将不同粒度语言转换为直觉模糊数,再利用相关算子集结;文献[8]利用离差最大化确定属性权重;文献[9-10]基于区间数相对熵建立线性规划求解属性权重;文献[11-12]采用多准则妥协解排序(VlseKriterijumska Optimizacijia I Kompromisno Resenje,VIKOR)法进行方案优选；文献[13-14]利用扩展的VIKOR方法在不确定语言环境下,融入决策者偏好进行方案优选。

针对专家权重未知且属性权重不完全条件下的多粒度语言多属性群决策问题,本文采用二元语义表示和转换函数方法一致化多粒度信息,避免信息集结的损失,利用有序加权平均算子(2-tuple ordered weighted averaging,T-OWA)和相对熵从客观角度求解专家和属性权重。改进灰色关联矩阵可以挖掘决策数据内在规律，而基于折衷思想的VIKOR方法可以明确刻画备选方案优劣，本文基于上述2种方法对方案排序,为解决上述问题提供一种新途径。

1相关基础理论

1.1不同粒度信息一致化处理

二元语义的定义、运算以及逆运算参见文献[9],下面简述基于二元语义表示的不同粒度的转换函数[10]。设不同粒度语言短语评价集为：

(1)

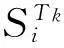
(2)

1.2二元语义有序加权平均算子

设{(s1,α1),(s2,α2),…,(si,αi),…,(sl,αl)}为一个二元语义的集合,则T-OWA算子[3]f定义如下:

(3)

其中,向量β=(β1β2…βl)T中的元素βi为集合{Δ-1(si,αi)|i=1,2,…，l}中按大小排在第i位的元素;h=(h1h2…hl)T为一个权向量,hi的表达式为:

且

(4)

其中,a,b,r∈[0,1]。在“多数”、“至少一半”和“尽可能多”原则下,模糊量化算子Q(r)对应的参数(a,b)分别为(0.3,0.8)、(0,0.5)、(0.5,1)。

2决策方法

2.1问题描述

2.2决策方法的原理与步骤

采用T-OWA算子集结专家评价信息,结合灰色关联评价矩阵,借鉴VIKOR方法的思想进行决策,具体步骤如下所述。

步骤1决策者k依据自身偏好选择语言集STl对备选方案xi的属性uj进行评价,结果用二元语义的形式表示评价矩阵如下:

(5)

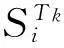
(6)

步骤2利用二元语义表示的集结算子T-OWA算子对决策者的评价信息进行集结,求得群组矩阵如下：

(7)

步骤3基于相对熵求解不完全条件下的属性权重wj=(w1w2…wn),对(7)式进行如下处理[10]。

则属性的正负理想值为：

(8)

则U+、U-分别称为归一化的正理想值和归一化的负理想值。

(4)在不完全权重信息下建立规划模型,具体公式如下:

(9)

(10)

(9)～(10)式确定方案的属性权重满足属性值与正理想解的相对熵越小且与负理想解的相对熵越大可得最优解。如果对模型中的2个目标函数同等看待，则可以将函数式转换为单目标形式,并用Matlab求解属性权重wj=(w1w2…wn)。

(11)

(2)选择理想方案x0,即

(12)

(13)

步骤5结合步骤3计算的属性权重wj=(w1w2…wn)和步骤4求得的灰色矩阵R=(rij,αij)m×n,借鉴VIKOR思想进行备选方案的排序。先计算群效用值(Qi,φi)和个体遗憾值(Pi,ψi),即

(14)

选择群效用值和个体遗憾值的理想值,即

(1)给出输入信号x(t)，设置迭代次数，通常情况下，迭代次数越高，分解越精确，但是同时所花时间也越长。将重建信号初始化置零。

(15)

计算整体的评价值γi为：

(16)

其中，λ为折衷系数,若λ>0.5,偏重于群体效用值来决策;若λ<0.5,偏重于个体遗憾值来决策；若λ=0.5，通过协商共识达成一致。

步骤6根据群效用值(Qi,φi)、个体遗憾值(Pi,ψi)和整体的评价值γi对方案排序,值最小的靠前,可得3种排序。

步骤7确定折衷方案,具体确定步骤如下:

如果γd值最小的方案xd满足下列2个条件,则认为方案xd为折衷方案。

条件1使用(Qi,φi)或(Pi,ψi),方案xd至少有一个最优。

条件2(γe-γd)≥1/(n-1),其中γe为γi第二小对应的方案。

如果只有条件1不能被满足,则折衷方案集为{γe,γd};如果条件2不能被满足,则求解不等式(γM-γd)<1/(n-1),确定最大的γM值,折衷方案集为γi取值在γd～γM所有方案的集合。

3算例分析

专家的权重向量未知,不完全条件下属性的权重如下:

0.15≤w1≤0.20,0.15≤w2≤0.20,

0.20≤w3≤0.25,0.2≤w4≤0.25,

0.20≤w5≤0.30

(17)

3位专家给出的决策矩阵如下:

(18)

首先用二元语义表示不同粒度语言的专家评价矩阵,选择粒度T3=9作为基本粒度语言,依据(2)式对其他2位专家的评价矩阵进行一致化处理;选用“至少一半”原则[9],即[a,b]=(0,0.5),根据T-OWA算子计算专家的权重Wg=(2/3，1/3，0),再通过对专家评价矩阵的集结可得：

由步骤3中(9)～(11)式计算得到各个属性的值如下:w1=0.15,w2=0.15,w3=0.25,w4=0.20,w5=0.25。

由步骤4中(13)式计算得到基于二元语义的灰色关联矩阵R=(rij,αij)m×n;综合上述求得的指标权重信息,由(14)～(16)式借鉴扩展VIKOR方法,求得群体效用值(Qi,φi)和个体遗憾值(Pi,ψi)分别为：

根据(16)式计算折衷排序值,当λ取不同的值,得到不同的总体评价排序结果,见表1所列。根据群体效用值(Qi,φi)对方案进行的排序如下:x4≻x3≻x1≻x2≻x5;根据个体遗憾值(Pi,ψi)对方案排序如下:x4≻x1≻x2≻x3≻x5,根据决策者的协商共识机制进行决策(即λ=0.5)时,总体评价值γi对方案排序为x4≻x1≻x3≻x2≻x5，方案x4在3种排序结果中均排在首位,x1在总体评价中为次优方案,且γ1-γ4=0.716≥[1/(5-1)]=0.25,满足VIKOR方法评选条件，所以方案x4为最佳方案。

为了进行对比分析，采用文献[12-13]的方法对上述算例求解。采用文献[12]中的TOPSIS方法得到唯一的排序结果为x4≻x1≻x3≻x2≻x5，与文中λ=0.5时计算结果一致。采用经典的VIKOR方法计算的结果[13]见表1所列。

由表1可看出,本文算法最优方案均小于文献[13]最优方案计算结果。由VIKOR方法原理可知,总体评价值越小方案最优,总体评价值越大方案越差。

与文献[12]的方法相比，本文算法增加了决策者的偏好系数,得到不同的排序结果，符合决策情境。与文献[13]的方法相比，本文算法评价值优于改进前的计算结果。因此本文方法具有合理性和有效性,为解决这类多粒度语言的多属性群决策问题提供了一种新途径。

表1　λ取不同值时对应各方案的折衷值及排序结果

4结束语

本文针对专家权重未知且属性权重不完全条件下的多粒度多属性群决策问题,给出了一种基于二元语义及改进VIKOR的方法。该方法既客观地求解专家权重和属性权重,又引入折衷系数体现了决策者的主观偏好,符合现实决策情境,并且通过与相关文献算例对比,证明了该方法的有效性和可行性。该方法可以应用于投资决策、方案设计等的方案比选。本文研究局限于属性独立的多属性群决策问题,而现实生活中属性间往往存在相互的关联作用,解决属性之间存在关联的多粒度群决策问题将是进一步研究的重点。

[参考文献]

[1]Herrera F，Herrera-Viedma E，Martinez L.A fusion approach for managing multi-granularity linguistic term sets in decision making [J].Fuzzy Sets and Systems,2000，114(1): 43-58.

[2]许韫玺,王要武,姚兵.基于熵理论的建设项目参与者多目标协同群决策模型[J].中国管理科学,2008,16(10):117-121.

[3]张爱萍,涂振坤.基于二元语义的不确定性多属性决策的4种集成算子[J].合肥工业大学学报：自然科学版，2013,36(4):506-512.

[4]Herrera F，Martinez L.A 2-tuple fuzzy linguistic representation model for computing with words[J].IEEE Transactions on Fuzzy Systems,2000,8(6):746-752.

[5]Herrera F，Herrera-Viedma E.Linguistic decision problems under linguistic information [J].Fuzzy Sets and Systems,2000,115(1):65-82.

[6]梁昌勇，戚筱雯,丁勇,等.一种基于TOPSIS的混合型多属性群决策方法[J].中国管理科学,2012,20(4):109-117.

[7]戚筱雯,梁昌勇,黄永清,等.基于混合型评价矩阵的多属性群决策方法[J].系统工程理论与实践,2013,33(2):473-481.

[8]王晓,陈华友,刘兮.基于离差的区间二元语义多属性群决策方法[J].管理学报,2011,8(2):301-305.

[9]张震,郭崇慧.基于相对熵的多粒度不确定型群决策方法[J].大连理工大学学报,2012,52(6):921-927.

[10]王晓,陈华友,周礼刚,等.基于相对熵的多粒度语言信息的多属性群决策方法[J].运筹与管理,2010,19(5):95-100.

[11]Opricovic S，Tzeng G H.Extended VIKOR method in comparison with outranking method[J].European Journal of Operational Research,2007,178(2):514-529.

[12]Opricovic S，Tzeng G H.Compromise solutions by MCDM methods:a comparative analysis of VIKOR and TOPSIS[J].European Journal of Operational Research,2004,156(2): 445-455.

[13]索玮岚.基于扩展VIKOR的不确定语言属性群决策方法[J].控制与决策,2013,28(9):1431-1435.

[14]韩仁东,郭鹏,赵静.主客观权重集成及扩展VIKOR的多属性群决策方法[J].计算机工程应用,2015,51(11):1-5.

(责任编辑闫杏丽)

Approach of multiple attributes group decision-making with multi-granularity linguistics

ZHANG Xiao-gang,ZHANG Liang,WANG Duan-min,ZHAI Nan-nan

(College of Equipment Management and Safety Engineering，Air Force Engineering University,Xi’an 710051,China)

Abstract:In view of multiple attributes group decision-making problem with multi-granularity linguistics,a new approach based on two-tuple linguistics and VlseKriterijumska Optimizacija I Kompromisno Resenje(VIKOR)is proposed. Firstly,the multi-granularity linguistic preference information is uniformed into the form of two-tuple linguistic information in basic linguistic term set. The unknown-attribute weight information of different expert and the incomplete weight information of attribute are determined by two-tuple ordered weighted averaging(T-OWA)operator and relative entropy. A new decision matrix,which is improved by gray relational coefficient to further investigate the inherent law of decision-making data,is used to characterize the optimal solution in VIKOR method. Finally,the feasibility and effectiveness of the proposed method are illustrated by the example.

Key words:multiple attributes group decision-making;two-tuple linguistics;gray relational matrix;relative entropy;improved VIKOR

收稿日期：2015-11-27；修回日期：2016-01-18

基金项目：国家自然科学基金资助项目(71401174)

作者简介：张小刚(1990-),男,甘肃天水人,空军工程大学硕士生; 王端民(1965-),男，陕西蓝田人,博士,空军工程大学教授,硕士生导师.

doi:10.3969/j.issn.1003-5060.2016.06.013

中图分类号:N945.25

文献标识码：A

文章编号：1003-5060(2016)06-0781-05