基于影响力传动的Kuramoto股市预测模型

戚国全,王　浩

(合肥工业大学 计算机与信息学院,安徽 合肥　230009)



基于影响力传动的Kuramoto股市预测模型

戚国全,王浩

(合肥工业大学 计算机与信息学院,安徽 合肥230009)

摘要:文章基于同步振子Kuramoto模型,提出了影响力传动的Kuramoto股市趋势预测模型(IT-KFM)。IT-KFM模型运用贝叶斯网络构建振子之间的结构关系,引入影响力传动,给出传动因子量化方法,将传动因子的传动参数加入到原Kuramoto模型中,进而根据不同振子间相位协方差的趋势变化分析和预测股市趋势,实验结果证明,IT-KFM算法相对于标准的SVM网络,在股票的走势预测方面有较好的预测效果。

关键词:Kuramoto模型;贝叶斯网络;股市预测;影响力;传动因子

股票市场具有高风险,有效的预测方法可以减少股民的投资风险。在相关研究文献中,一些传统的时间序列模型被用于预测股票趋势,如AR(autoregressive)模型、ARMA(autoregressive moving average)模型、GARCH(Generalized Autoregressive Conditional Heteroskedasticity)模型及其改进模型等[1-2],但是这些模型是在假设股票时序数据是正态分布和平稳的情况下进行分析的[3-4],因此这些模型不能有效地对股票数据进行预测。为了提高预测精度,文献[5]从数据挖掘角度将ANNs(artificial neural networks)模型与传统时序模型相结合预测国家经济态势,能够避免数据非常态分布对模型的影响,然而ANNs模型在预测股票方面具有模型控制参数多、过度学习风险等缺点,容易陷入局部最小陷阱。SVR(support vector regression)模型因其遵循结构风险最小化原则[6],股票价格中包含了很多有价值的信息,有效地分解和聚合信息能够提高预测精度[7]。文献[8]对股票价格波动信息进行分析,提取波动数据中的特征,结合ARCH(Autoregressive Conditional Heteroskedasticity)模型进行预测,但是该模型没有很好运用先验知识。

已有研究表明,从不同快慢级别股市分时线价格的波动趋势中能够发现股票价格趋向于同步的特征[9]。Arthur Winfree假设每个振子只与它周围有限个振子之间存在强力作用,这样振子的幅值变化可以忽略,从而将同步问题简化成研究相位变化的问题,为同步现象做了奠基性的工作[10]。1975年,统计物理学家Yoshiki Kuramoto对Winfree模型进行了简化,提出了Kuramoto模型[11-12],该模型对于不同振子从不同步到同步的过程可以较好地形式化体现。近年来,Kuramoto模型也广泛用于群体行为的数学建模与分析,特别是针对群体之间同步特征的分析和研究。

本文针对现有的股票价格预测方法,基于同步振子Kuramoto模型,提出影响力传动(influence transmision,IT)的Kuramoto股市趋势预测模型(IT-KFM),算法在股市不同的分时线数据上构建股市Kuramoto振子网络结构,不同振子之间经过影响力传动而趋向同步,根据不同振子间的同步性能来分析和预测股市趋势。最后,IT-KFM算法在上证大盘交易数据上的实验结果显示出算法的实用性和有效性。

1贝叶斯网络

贝叶斯网络(Bayesian networks,BNs)利用有向无环图表示变量之间的概率依赖关系。贝叶斯网络是一个二元组B=(G,θ),G=(X,E)是一个有向无环图,其中X=(X1,…,Xn)是随机变量集,而E表示结点集合X中结点间的一一对应的关系,E是一个有向边集。参数集θ=(θ1,…,θn)为条件概率分布集,θi=P(Xi|Pa(Xi))表示结点Xi的概率分布,Pa(Xi)表示结点Xi的父结点集。对于BN中的每个节点Xi,在给定的Pa(Xi)的情况下,Xi条件独立于其他任何非子孙节点。因此,BN中变量集X的联合概率分布可表示为:

(1)

在网络学习过程中,通常假定网络中所有的变量是离散变量或是呈高斯分布的连续变量[13-16]。但是,股市不同分时线振子的涨幅变量并不是服从高斯分布的连续变量,因此需要考虑对连续变量进行离散化[17]。

2Kuramoto模型的概念

Kuramoto模型把网络中每个点看作一个相位振子,设有N个相关变量(包括快慢速变量)的相位振荡器(Z1,Z2,…,ZN),表示为θi(t),i=1,…,N,第i个节点的相位为θi(t),它的自然频率是ωi,网络中所有节点自然频率的分布由密度函数g(ω)决定,节点i的行为可以用(2)式描述:

(2)

其中,k为耦合强度;e(Zi,Zj)表示2个不同振子Zi、Zj之间的影响力传动参数。当耦合被引入后,振子间会有相互作用(耦合),每个振子不仅独立地按照其自然频率运动,同时受其他个体行为的影响,因此能逐渐与其他个体产生同步。在Kuramoto模型中,耦合项是对称的而且依赖于振子间的相位差而不是振子的相位。

“耦合强度”k对于多个相关振子能否达到锁相(锁频)状态具有较大的决定性作用。存在一个临界的耦合强度kc,当k=kc时,各振子能快速达到锁相的状态。

3基于影响力传动的Kuramoto股市预测

同步是自然界各种集体现象中最基本的行为之一,许多集体行为的内在机制都与同步有着直接的关系。同样在股市市场中,同步现象也可以解释和分析股市的一些现象和趋势,本文将Kuramoto模型应用于股市市场中的同步特征研究。

基于Kuramoto模型,本文将股市中的5根分时线(5、15、30、60 min和日线)收盘价数据分别作为振子网络结构的5个振子系统,从实时的交易数据和技术指标中提取出振子之间重要的影响力参数,经过网络结构和参数的学习,最后通过研究它们之间的相互耦合相位的集体动力学的同步性能来对目标振子的趋势进行预测。

3.1收盘价涨幅

股票指标是运用一些复杂的数学公式,用数据来论证股票趋向、买卖的分析方法的一种工具。股票交易数据CP=(CP1,CP2,…,CPn),其中CPi记录的是股票每个交易节点的收盘价。

收盘价涨幅用收盘价的每个节点的涨幅大小来表示股市的涨跌趋势大小,涨幅的计算公式如下:

(3)

采用(3)式计算后并将收盘价涨幅进行离散化的结果见表1所列。

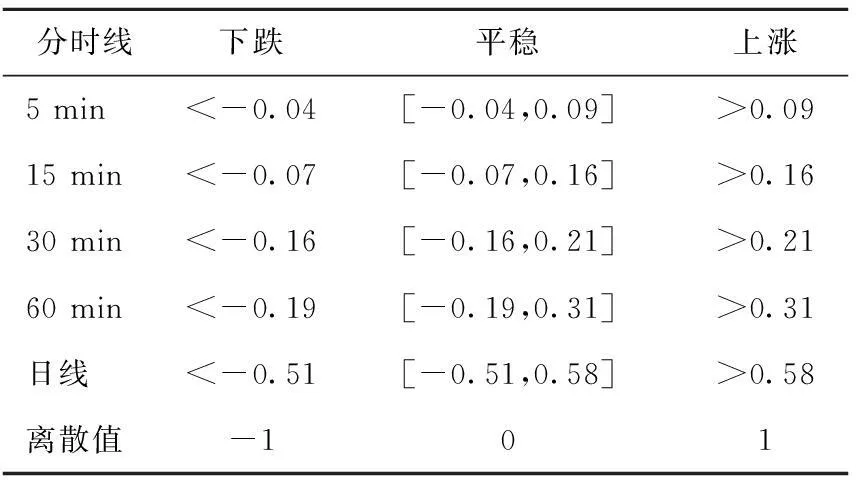
表1　分时线收盘价离散化区间　%

3.2影响力

在Kuramoto振子模型中,不同的振子之间因为有耦合作用,才会使得振子的相位趋向于同步。同样在股市中,股票不同的分时线之间因为存在耦合作用才使得它们的股市涨跌趋势趋于同步。

影响力为存在于分时线之间的,从一个分时线的股市交易数据提取出来的并且能在不同分时线振子之间产生传动作用的一种耦合作用。影响力能对另一个分时线的走势产生传动作用,使得分时线振子的相位发生变化。

根据对股市市场趋势的特征分析,得到日线和各个分时线交易数据中的成交量、成交额等体现股市上涨下跌的相关技术指标。考虑成交量比较容易作假,特别是在放量的时候,控盘主力利用手中的筹码大手笔对敲等操盘手段来进行放量,所以在文中没有采取成交量指标作为影响力因子。

对于股票分析,移动平均线是目前运用最为广泛的技术指标,它是对收盘价进行平均后生成的一条曲线。

股市指数有效突破压力线和支撑线也能很好地支持股市上涨趋势。在上涨阶段,对于几根重要的移动平均线(MA5、MA30、MA60),实时股价一般会有效地突破股市中的移动平均线,在移动平均线图形中,也能看到会出现利于股市走势的有效金叉,特别是短期平均线突破中长期移动平均线时,能够对于股市的上涨趋势产生很大的影响力。考虑到它会受到当前股市所处的一个股市平均行情影响,不能用移动平均线之间的距离直接作为影响力传动因子,所以采取了相对均线距离作为影响力传动因子。

根据上面的分析和几个比较明显的特征,可以从对股市不同分时线数据产生影响的几个技术指标中提取影响力传动参数。

3.3影响力传动因子

MA5、MA30、MA60、MA120分别是股市中的移动平均线指数,MA120是近期较长一个时间段以内股市数值所在的一个平时点位,下面公式中除以MA120是为了消除当前股市点位对均线距离的影响,影响力传动因子即相对均线距离d1、d2计算公式如下:

d1=(MA5-MA60)/MA120,

d2=(MA30-MA60)/MA120

(4)

根据移动平均线的定义公式,可以推导得出:

(5)

(6)

在波动的股市市场中,随着每一天股价的不断变化,相对均线距离d1、d2也在不断波动,d1表示影响力大小比d2要大,它影响的距离也相对比d2要近,所以在后面将d1作为构建的振子网络节点中相邻节点之间的影响力参数,d2表示间隔节点之间的影响力参数。传动因子d1、d2每2个分时线之间表示下跌、平稳、上涨的影响力对应趋势离散化区间,见表1所列。

3.4影响力传动的Kuramoto模型形式化

3.5协方差

协方差分析是建立在方差分析和回归分析基础之上的一种统计分析方法。方差分析是从质量因子的角度探讨因素不同水平对实验指标影响的差异。一般地,质量因子是可以人为控制的。回归分析是从数量因子的角度出发,通过建立回归方程来研究实验指标与1个(或几个)因子之间的数量关系,具体计算公式如下:

(7)

当Cov(X,Y)>0时,表明X与Y正相关,且协方差值越大,正相关性越显著;当Cov(X,Y)<0时,表明X与Y负相关,且协方差值越大,负相关性越显著;当Cov(X,Y)=0时,表明X与Y不相关。

3.6影响力传动的Kuramoto股市预测算法

IT-KFM算法是基于动力学同步Kuramoto模型,通过贝叶斯网络K2学习算法学习网络的结构关系,利用Kuramoto模型进行同步性计算,然后用协方差去衡量网络中不同振子之间的同步性,通过对同步性能的分析,实现对股市的趋势预测。

IT-KFM算法的输入为股市交易数据集Dataset，输出为预测股票日线涨跌趋势结果分布。具体步骤如下:

(1)用收盘价涨幅公式将股票收盘价格转化为每个节点的涨幅。

(2)将Dataset分成训练数据集Train-Data和测试数据集Test-Data。

(3)按照表1中的离散化标准,根据股市的涨跌行情,对节点涨幅进行合理离散化。

(4)对离散化的节点涨幅数据用贝叶斯网络k2/bnpc学习算法学习股市初步的振子网络结构,回归分析不同振子之间的涨幅,删除结构中关联作用很小的边,优化振子网络结构,得到每个振子的形式化表达式。

(5)加入影响力传动因子,学习最优的耦合强度系数kc,确定网络中振子之间的影响力传动参数,根据Kuramot模型传动方程,分别计算影响力传动后各个振子的相位波动状态。

(6)根据协方差公式衡量振子同步性能,通过协方差的趋势大小分析和预测股市趋势,并与真实股市涨跌趋势和SVM模型预测结果进行对比。

(7)预测结果分析并评价。

4实验数据处理以及结果分析

4.1下载上证大盘数据

实验数据是在Matlab Version 7.11 R2010b软件环境下,利用贝叶斯工具包FullBNT-1.0.4,从大智慧客户端下载的。下载的数据包括2012年10月17日至2013年6月7日一共155个交易日,分别有5 min分时线数据7 440个、15 min分时线数据2 480个、30 min分时线数据1 240个、60 min分时线数据620个和155个日线交易数据,分别下载了对应的收盘价、MA5、MA30、MA60、MA120、boll等指标数据。

4.2K2算法结构学习和回归分析优化网络

首先根据上面分时线收盘价涨幅进行离散化,这里是5个节点的贝叶斯网络,用K2算法进行结构学习和参数学习,目标节点是日线节点5,得到学习的初步网络结构如图1a所示。分别分析和计算网络存在有向边的节点之间的相关系数,得出振子间的相关系数分别为:

correl(1,2)=0.475 6，correl(1,3)=0.293 4，

correl(1,4)=0.250 2，correl(2,3)=0.557 6，

correl(2,4)=0.465 9，correl(2,5)=0.190 8，

correl(3,4)=0.624 8，correl(3,5)=0.394 5，

correl(4,5)=0.486 6。

从以上数据可看出,节点对(1,3)、(1,4)、(2,5)之间的相关系数小于0.3,属于显著不相关范畴,所以删除它们之间的边,得到优化结构图如图1b。

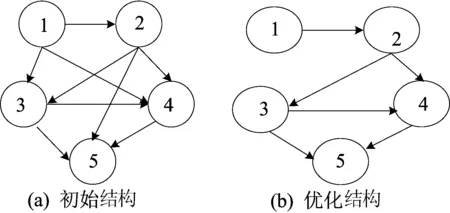
图1　振子网络结构

由图1a和图1b对比中可以直观地看出,分时线数据节点间隔时间比较长的振子之间的影响力参数会变得很小,网络结构经过优化之后,更加符合振子耦合网络结构图的实际情况。

根据以上形式化可以得出该振子网络的每个振子的表达式如下:

4.3最优耦合强度kc的学习

分别将影响力传动因子d1、d2代入到有边相连的振子之间,d1作为相邻振子影响力参数,d2作为不相邻振子间的传动影响力参数,针对整个数据集dataset,学习初步Kuramoto模型中公式最优的耦合强度kc,训练的数据集是2012-10-17—2013-06-07这个时间段内的股市交易数据,股市5个分时线振子之间的协方差的波动图如图2所示。

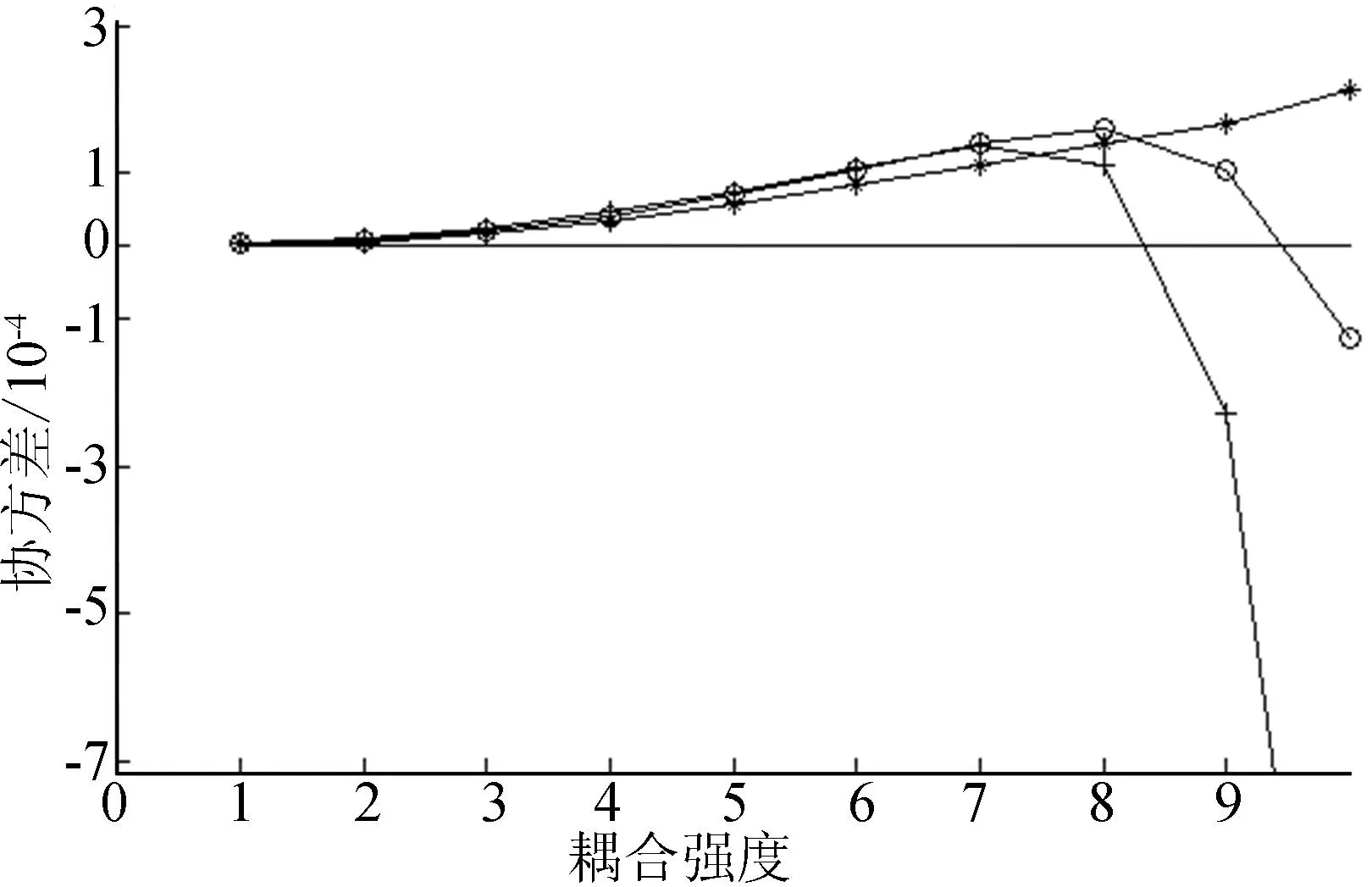
图2　协方差与耦合强度系数

由图2可以看到出k=8时,网络振子之间达到最优的同步效果。

4.4模型训练和数据预测

数据训练集和测试集见表2所列,将股市按上涨、调整、下跌的趋势分为以下几段在Matlab中进行实验测试,根据表1中日线涨幅的离散化的参数区间,最终得到日线股市趋势的预测结果,预测趋势与真实趋势的对比如图3所示。

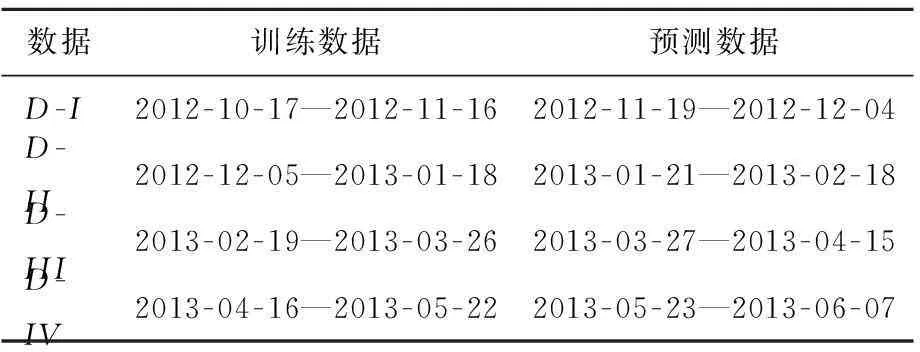
表2　数据训练集和测试集

4.5SVM模型对比实验

本文使用的SVM版本是libsvm-2.9,其中svm-scale.exe是用来对原始样本进行缩放的;svm-train.exe主要实现对训练数据集的训练,并可以获得SVM模型;svmpredict.exe 是根据训练获得的模型对数据集合进行预测。分别按照表2所列的训练集数据和测试集数据进行实验,得到股市趋势预测精度与IT-KFM算法进行对比,具体结果见表3所列。

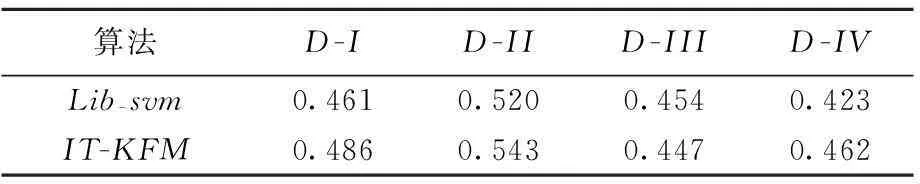
表3　预测精度对比实验结果

4.6实验结果分析

将协方差的数值用于股市交易日中不同的分时线中,图3中的协方差波动图分别表示股市在不同时长的波动趋势中15、30、60 min和日线的涨跌趋势关系密切程度。协方差为正值,说明这几个快速分时线与日线的波动是正相关的,大小用于衡量不同的分时线同步程度;当协方差的数值达到峰值,表明股市一个交易日中的各种分时线的波动趋势实现同步,此时(根据整个通道的涨跌趋势)日线的波动趋势也达到了峰值。通过对协方差数值和股市日线交易日数据的对比,可以对股市的日线涨跌趋势进行一定程度的预测。

根据本文算法预测结果分析可见,IT-KFM算法对于大幅波动的股票走势预测具有较好的效果,且算法误差可控;表3显示,IT-KFM能有效提高准确率。另外,算法已在股市大数据智能分析网站、宏大数据网(www.ihdsj.com)中进行了实际应用。

5结束语

本文基于同步振子Kuramoto模型,提出了影响力传动的Kuramoto股市趋势预测模型(IT-KFM),运用贝叶斯网络学习,将影响力因子作为网络间的耦合参数,根据不同分时线振子间的同步特性分析和预测股市趋势。实验结果表明算法对于股市的趋势可以进行一定程度的分析和预测,但是由于股市中受经济政策影响较大,有些突变趋势难以预测,准确率还不够高。

[参考文献]

[1]王宇新. GARCH模型和SV模型对深圳股市的比较[J]. 合肥工业大学学报:自然科学版,2007,30(6):743-745.

[2]何帮强,惠军.基于ARMA-EGARCH-M模型的沪深股市波动性分析[J]. 合肥工业大学学报:自然科学版,2007,30(7):864-868.

[3]Kazem A,Sharifi E,Hussain F K,et al. Support vector regression with chaos-based firefly algorithm for stock market price forecasting[J]. Applied Soft Computing,2013,13(2):947-958.

[4]Yi Zuo,Kita E. Stock price forecast using Bayesian network[J].Expert Systems with Applications,2012,39(8):6729-6737.

[5]Kao L,Chiu C,Lu C,et al. Integration of nonlinear independent component analysis and support vector regression for stock price forecasting[J].Neurocomputing,2013,99(1):534—542.

[6]Vapnik V. The nature of statistical learning theory[M]. New York:Springer-Verlag,1995.

[7]Cai C X,Kyaw K,Zhang Qi. Stock index return forecasting: the information of the constituents[J]. Economics Letters,2012,116(1):72-74.

[8]Taylor S J,Yadav P K,Zhang Yuanyuan. The information content of implied volatilities and model-free volatility expectations:evidence from options written on individual stocks[J]. Journal of Banking &Finance,2010,34(4):871-881.

[9]王杰. 我国股市投机性与股价波动同步性研究[D].济南：山东大学,2013.

[10]吴真，王倩.中国股市股票回报同步效应研究[J].中国集体经济,2009(24):96-99.

[11]郑志刚,李晓文,张廷宪. 同步现象:Kuramoto模型及其他[C]//全国复杂系统研究论坛论文集，2005：379-394.

[12]胡鑫.爆发式同步的广义Kuramoto模型的解析求解[D].上海：华东师范大学,2014.

[13]Jaeger M. Parameter learning for relational Bayesian networks[C]//Proc of the 24th International Conference on Machine Learning,2007: 369-376.

[14]Su J,Zhange H,Ling C X,et. al. Discriminative parameter learning for Bayesian network [C]//Proc of the 25th International Conference on Machine Learning,2008: 1016-1023.

[15]de Campos C P,Ji Q. Improving Bayesian network parameter learning using constraints [C]//Proc of the 19th International Conference on Pattern Recognition,2008:113-120.

[16]Chang R,Wang W. Novel algorithm for Bayesian network parameter learning with informative prior constraints [C]//Proc of the International Joint Conference on Neural Networks,2010:1-8.

[17]王飞,刘大有,薛万欣. 基于遗传算法的Bayesian网中连续变量离散化的研究[J]. 计算机学报,2002,25(8):794-800.

(责任编辑万伦来)

Stock market Kuramoto forecasting model based on influence transmission

QI Guo-quan,WANG Hao

(School of Computer and Information,Hefei University of Technology,Hefei 230009,China)

Abstract:Based on the synchronous vibrator Kuramoto model,a stock market trends forecasting model with influence transmission(IT-KFM)is presented. In IT-KFM algorithm,Bayesian network is utilized to build the structural relationships between the oscillators,and the influence transmission is introduced. Then the quantitative method of transmission factor is given,and the transmission parameters of transmission factor are added to the original Kuramoto model. Finally,the stock market trends are analyzed and forecasted according to the trend change of the covariance between different oscillator phases. The experimental results show that the performance of the proposed method is better than the standard SVM algorithm in stock trend forecast.

Key words:Kuramoto model;Bayesian network;stock market forecast;influence;transmission factor

收稿日期：2015-03-09；修回日期：2015-04-03

基金项目：国家自然科学基金资助项目(61070131;61175051;61175033)

作者简介：戚国全(1988-),男,湖北武穴人,合肥工业大学硕士生;

doi:10.3969/j.issn.1003-5060.2016.06.009

中图分类号:TP301.6；F830.91

文献标识码：A

文章编号：1003-5060(2016)06-0761-06

王浩(1962-),男,江苏泰州人,博士,合肥工业大学教授,博士生导师.