线性模型有偏估计的一种新算法

梁飞豹,林同华

(福州大学 数学与计算机科学学院,福建 福州　350108)



线性模型有偏估计的一种新算法

梁飞豹,林同华

(福州大学 数学与计算机科学学院,福建 福州350108)

摘要:文章以降低预测残差平方和为目标,基于岭估计增大回归系数矩阵的对角元素的思想,提出一种利用高斯消去变换工具的线性模型参数估计法,并进行数据模拟实验,最后通过平均预测残差平方和以及平均残差平方和的箱线图来对比新算法和最小二乘估计及岭估计的优良性,说明满足一定条件时,新算法在估计精度和稳定性上优于这2种方法。

关键词:预测残差平方和;参数估计;岭估计;高斯消去;箱线图

考虑线性模型(Y,Xβ,σ2I):

(1)

为了减小线性模型的奇异性问题,研究者引入有偏估计，常见的有偏估计有压缩估计、Liu估计、主成分估计、岭估计等。其中,压缩估计[3]是对LS估计的均匀压缩,它解决了因设计矩阵复共线性强而得到绝对值太大的参数估计的问题;但所含的表达式包含未知参数β,实际过程中对它的估计存在一定的难度,并且在以MSE(mean squared error)作为估计的优良性准则时,压缩估计优于LS需要回归因子的复共线性不能太强。Liu估计[4]是关于LS估计的线性变换,但它的估计取值依赖于最小二乘估计。主成分估计[5]在减少对系统影响较小的自变量个数的同时也降低了与参数真值间的均方误差,是一种线性约束下的最小二乘的解;但在主成分估计的过程中,XTX的特征值λi≅0说法较笼统,如何保留主成分的个数是个重要的问题。岭估计[6]是在设计阵计算中引入偏参数k,通过对岭参数k的合理取值有效地改善复共线性所带来的病态性;而偏参数k扩展成偏参数矩阵K,又得到广义岭估计。关于岭参数的选择,方法众多[6-8]。在实际工作中,岭估计是运用较为广泛的一种有偏估计,许多研究者对岭估计做了不同程度的改进,以期望缩小均方误差、提高精度。2007年,Kaciranlar将压缩估计和Swindel提出的修正岭估计相结合,提出了两参数估计[9],它是最小二乘估计、岭估计、Liu估计、压缩估计的综合。2010年,杨虎和常新峰综合岭估计和Liu估计提出另一种两参数估计,并在MSE准则下证明了该估计的优良性[10]。

现有的有偏估计还难以找到一个最好的估计,使得这个估计在有偏估计类中关于均方误差最小。本文从近似奇异矩阵的求逆问题角度出发,提出一种新的线性模型有偏估计。

1高斯消去变换

(2)

性质1Tkk(Tkk(A))=A,即对A连续施行2次消去变换,其结果都是A不变。

性质2Tkk(Tll(A))=Tll(Tkk(A)),即对A施行2次消去变换,顺序交换,其结果相同。

性质3Tkk{Tll[Tmm(A)]}=Tmm{Tll[Tkk(A)]},即对A施行3次消去变换,结果与顺序无关。

性质4A-1=Tpp{T(p-1)(p-1){…T11(A)}},即按顺序对p个对角元素作消去变换,得到逆矩阵。

对于线性模型(1)式,观察增广矩阵A=(XTXXTY),当XTX可逆时,对增广矩阵A施行消去变换T11,T22,…,Tpp后,由(2)式可得:

可以看到此时矩阵B的最后一列即为线性模型(1)式的最小二乘估计。

由(2)式可知,在每次消去变换时主元充当分母,如果主元太接近于0,计算机运算过程中将不可避免地产生舍入误差,其累积将产生较大的相对误差。因此对增广矩阵A施行消去变换,应尽量避免选择太小的主元。例如,每次选择绝对值最大的未作变换的对角元素作为主元。

(3)

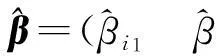
(4)

因此,LS估计的消去变换其实就是逐渐添加变量因子与观测向量Y构成线性方程并求解回归系数的过程,没有考虑逐渐添加的变量因子与Y的线性关系而仅以对角元素的大小作为主元选取的原则,有失客观。考虑到自变量因子与观测向量的线性关系,本文采用逐步添加对观测向量方差贡献率最大的自变量因子与之构成线性方程的方法,相应地,便确定了每次选择主元的原则。

然而,在XTX接近奇异时,即det(XTX)近似于0,此时不管如何确定选取主元的原则,由Tkk变换的性质5可知,必然存在某个主元接近于0,这时将产生较大误差。针对此情况,岭估计适当增大设计阵所有对角元素的值,使得原本近似于0的特征根变大;并且由于增加量并不大,矩阵本身未作太大变化,但复共线性降低,此时得到的参数估计在均方误差意义下优于LS估计。基于此思想,本文利用交叉检验思想,在每次消去变换前适当增大主元的大小使得预测效果最优。

2新算法

在线性模型(1)式中,设X、Y已作中心化,假设已将样本C=(XY)分成3份,即C1=(X1Y1),C2=(X2Y2),C3=(X3Y3)。其中,C1为n1×(p+1)矩阵;C2为n2×(p+1)矩阵;C3为n3×(p+1)矩阵。

2.1数据处理

(5)

其中,R(0)表示未作高斯消去变换时相关阵的增广矩阵,而下述出现的R(l)则表示已作l次高斯消去变换后的增广矩阵。

2.2循环过程

(1)主元选择。计算所有未选的变量因子的方差贡献,即

(6)

其中,Q={1,2,…,p};L为已选择添加的变量因子的下标集;l为已作高斯消去变换的次数。显然,第1次选择添加变量因子时,L=∅,l=0。

(7)

(8)

2.3循环结束

(9)

(10)

3算例

现有一样本数据矩阵,将其分成训练样本和检验样本2份。假设已中心化样本矩阵,训练样本C1=(X1Y1),检验样本C2=(X2Y2),其中,X1、Y1、X2、Y2分别为:

将训练集样本转化为相关矩阵:

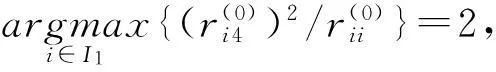
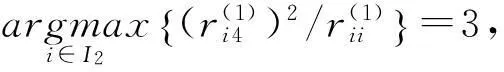
此时得到标准模型回归系数为：

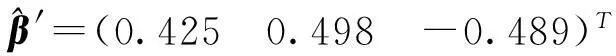
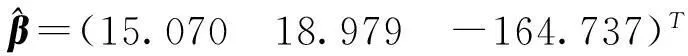
4实验模拟

通过蒙特卡罗模拟法来验证新算法的优良性,以维数p=5为例,在总体G:X～Np(0,Σ)中随机抽取样本容量为n的自变量样本矩阵X,其中协方差矩阵Σ为:

其中,ρ为自变量样本的自相关系数,介于0和1之间,它控制着任意2个自变量因子的相关性。

因变量的观测值通过(11)式获得:

(11)

其中,εi为独立正态分布(0,σ2)伪随机数;σ为随机误差的标准差;β=(3.01.50.80.1-2.0)T为固定向量。

考察在σ和ρ的6种不同取值情况下,新算法、LS估计以及岭估计在σ=0.8,1.2,1.5,ρ=0.900,0.999时的各自估计效果。

在总体 G中随机生成3份样本容量分别为n1=20,n2=100,n3=200的自变量样本矩阵X1、X2和X3,按(11)式生成因变量观测矩阵Y1、Y2和Y3。

对得到的3份样本按上述算法设计进行计算。在每个给定的参数σ和ρ中,这样的模拟计算都重复进行100次。

采用重抽样法,在3种方法各自得到的100份平均残差平方和(MRSS)与100份平均预测残差平方和(MPRESS)中,各随机抽取500份数据,并求出中位数和标准差,见表1和表2所列。

接着生成6种σ和ρ不同取值时3种估计法的平均残差平方和以及平均预测残差平方和的箱线图,限于篇幅,本文只选取2种有代表性的箱线图,如图1、图2所示。

由表1中可以看到,在重抽样下,自变量样本矩阵自相关性ρ很大(复共线性很强),新算法的参数估计平均残差平方和的中位数和标准差都小于岭估计。

由表2中可以看到,在重抽样下,当自变量样本矩阵的自相关性越强,随机误差的标准差σ2越大时,新算法的平均预测残差平方和的中位数和标准差都要小于LS估计和岭估计。

表1　3种算法模拟数据平均残差平方和(MRSS)的中位数和标准差比较

注:括号内的数值为平均残差平方和的标准差。

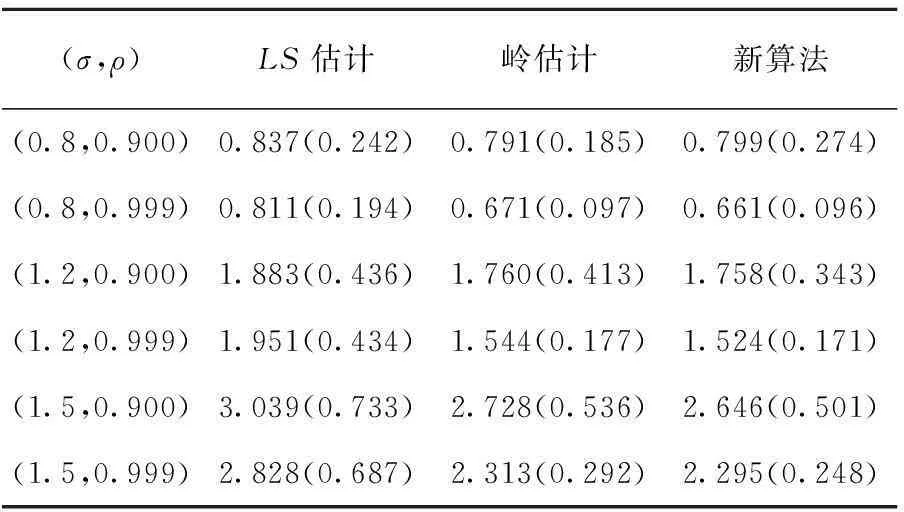
表2　3种算法模拟数据平均预测残差平方和(MPRESS)的中位数和标准差比较

注:括号内的数值为平均预测残差平方和的标准差。

另外从箱线图中可以看到,在自变量样本矩阵自相关系数足够大时,新算法估计的平均残差平方和以及平均预测残差平方和都小于岭估计,并且四分位距也小,误差显得更为稳定。

因此,当线性模型的随机误差的方差和自变量样本自相关性较大时,新算法下的线性模型参数估计的预测结果无论是精度还是稳定性都好于LS估计和岭估计,是一个更为优良的估计。

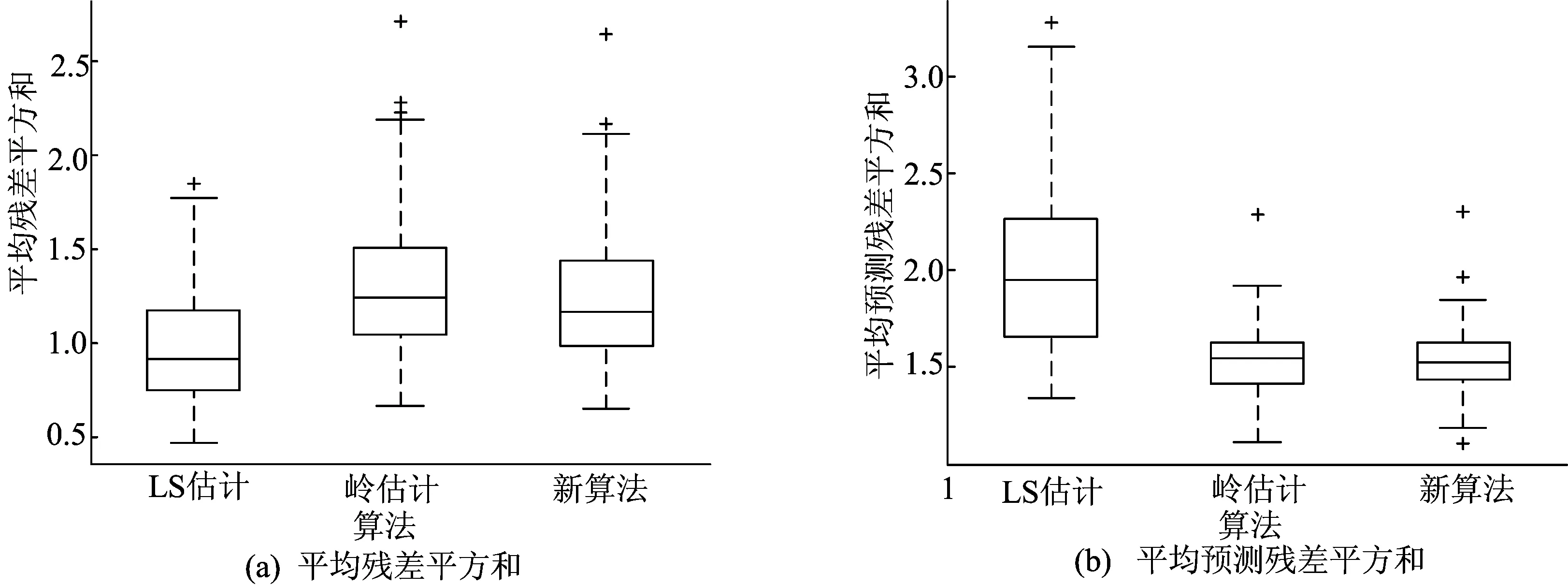
图1　σ=1.2,ρ=0.999时的箱线图

图2　σ=1.5,ρ=0.999时的箱线图

5结束语

对于线性方程组,为了减小最小二乘估计所得回归系数的误差,需要先做降低病态系数矩阵条件数的预处理,又由于变量x1,x2,…,xp的量纲可能差异很大,使得XTX不同对角元素的所需增量差异巨大。本文先将XTX转换成相关矩阵的形式,利用逐渐添加最关键变量因子的原则选取相应的主元,再利用交叉检验思想,作增大后高斯消去变换；在Matlab中采用蒙特卡洛模拟法进行数值实验。通过与LS估计以及一般岭估计比较,新算法在复共线性较强时的预测效果和稳定性都好于另外2种;但交叉检验的过程对样本数据的切分方法存在着人为因素,并且由于过程相当于逐步增加变量建立方程,在运算速度上慢于一般岭估计。本文只给出一种新算法,严格的理论性质将是今后的研究工作方向之一。

[参考文献]

[1]陈希孺,王松桂.线性模型中的最小二乘法[M].上海:上海科学技术出版社,2003:1-12.

[2]陈希孺,王松桂.近代回归分析:原理方法及应用[M].合肥:安徽教育出版社,1987:218-226.

[3]张金槐.线性模型参数估计及其改进[M].第2版.长沙:国防科技大学出版社,1999:68-72.

[4]Liu K.A new class of biased estimate in linear regression[J]. Commun Stat Theory Methods 1993,22:393-402.

[5]Massy W F. Principal components regression in exploratory statistical research[J].J Amer Statist Associ,1965,60: 234-266.

[6]Hoerl A E,Kennard R W.Ridge regression: biased estimation for non-orthogonal problems[J]. Techometrics,1970,12: 55-68.

[7]Al-Hassan Y M.Performance of a new ridge regression estimator[J].Journal of the Association of Arab Universities for Basic and Applied Sciences,2010,9:23-26.

[8]Khalaf G.A proposed ridge parameter to improve the least squares estimator[J].Journal of Modern Applied Statistical Methods,2012,11:443-449.

[9] 殷艺芸.线性模型中Liu估计及两参数估计的进一步研究[D].重庆:重庆大学,2012.

[10]常新锋.线性模型参数有偏估计的若干研究[D].重庆:重庆大学,2011.

[11]方开泰,全辉,陈庆云.实用回归分析[M].北京:科学出版社,1988:70-78.

(责任编辑张淑艳)

A new algorithm of biased estimation in linear model

LIANG Fei-bao,LIN Tong-hua

(College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350108,China)

Abstract:In order to reduce the prediction residual sum of squares,and based on the method of ridge estimation that increases the diagonal elements of the regression coefficients matrix,a linear model parameter estimation method using the tool of Gaussian elimination transform is proposed. And the data experiment is carried out. Finally,its boxplots about the mean prediction residual sum of squares and the mean residual sum of squares are compared with those of the least squares estimation and the ridge estimation,and the results show that the new algorithm performs better than these two estimations in the estimation precision and stability under certain conditions.

Key words:prediction residual sum of square;parameter estimation;ridge estimation;Gaussian elimination;boxplot

收稿日期：2015-07-22；修回日期：2015-10-13

基金项目：国家自然科学基金资助项目(11301084);福建省自然科学基金资助项目(2014J01010)

作者简介：梁飞豹(1963-),男,福建莆田人,福州大学副教授,硕士生导师.

doi:10.3969/j.issn.1003-5060.2016.06.027

中图分类号:O212.1

文献标识码：A

文章编号：1003-5060(2016)06-0854-05