基于功率潮流分析的电能计量新方法

张晓冰，　李云辉，　曹伟

(哈尔滨理工大学 测控技术与通信工程学院，黑龙江 哈尔滨 150080)



基于功率潮流分析的电能计量新方法

张晓冰，李云辉，曹伟

(哈尔滨理工大学 测控技术与通信工程学院，黑龙江 哈尔滨 150080)

摘要:针对非平稳畸变信号条件下电能准确合理计量问题，在非线性负载泛函级数模型的基础上，进行了功率潮流分析并提出畸变信号条件下电能计量新方法。根据泛函级数理论中Wiener核与Volterra核转换定理求得负载的Volterra核，应用Volterra级数理论将正弦输入信号条件下负载输出电流与电压用Volterra泛函级数表示。利用小波分解与重构算法对电流与电压信号进行分解与重构，求出功率潮流分析所需电流与电压的基波分量与畸变分量。结合IEEE-Std1459-2010标准定义，以半导体整流器、电力机车及两者组成的复合系统为例，对非线性负载进行功率潮流分析，依据各功率潮流的物理意义及潮流方向，提出畸变信号条件下电能计量新方法。仿真结果表明非线性负载功率潮流仿真结果与理论结果一致，基于功率潮流分析的电能计量新方法能够实现畸变信号条件下电能的合理计量。

关键词:电能计量;功率潮流;泛函级数; 负载模型；小波分析

0引言

随着非线性负载的不断增加，电网信号畸变愈加严重，这导致负载与电网之间产生了复杂的能量交换，使得电能的准确合理计量变得更加困难[1-4]。非线性负载电能用户在消耗电能的同时，还作为畸变功率源向电网注入畸变功率，使公共连接点的电压波形严重畸变，导致电网电压波动，产生瞬时脉冲等各种电能质量干扰，对电网、敏感电气设备的正常运行造成了严重影响，因此对这些负载的电能计量方式应该进行深入的研究和探讨[5-8]。科学而合理的电能计量方法应该依据功率潮流的检测分析结果，确定污染源，将注入电网的畸变功率及其电能单独计量，并将其计入到总的电能中去，而目前的电能计量方法及仪表均不能满足这种计量的需要。在当前电网信号严重畸变的现状下，如何准确合理地计量功率及电能已经成为电气测量技术及仪器仪表研究领域急需解决的问题。研究和完善畸变信号条件下功率及电能计量的理论，既是电路理论中一个重要的基础性研究课题，也是解决现代电力系统中功率及电能测量问题的理论基础。

对不同特性的负载进行电能计量时，目前的计量方法存在着不合理的问题。例如在谐波条件下，按传统的计量方式，线性负载用户不仅要支付基波电能的费用，还要负担对其毫无意义而且有害的、被迫吸收的谐波电能的费用；而非线性负载则相反，它向供电系统注入谐波，污染电网，但却少负担由其注入的谐波电能的费用[9-10]。从效果上看，这种电能计量方式起到了鼓励用户向系统注入谐波的作用，显然对提高电网电能质量极为不利。比较合理的方法是采用基波电能表的技术方案，它已经成功应用到非线性负载的电能计量中，并取得了一定的成果[11]。但谐波条件下的电能计量理论、方法和仪表解决不了更具普遍性的畸变信号条件下电能准确合理计量的问题[12]，因为谐波模型并不能真实反映电网信号的实际情况，尤其是冲击性负载等非线性负载产生的非平稳电压、电流信号根本无法用谐波信号的数学模型来描述[13]。

本文在研究了畸变信号条件下电网信号的特性和泛函级数理论的基础上[14]，应用Wiener泛函级数建立了电网信号通用的数学模型，该模型解决了畸变信号条件下电网信号统一描述的问题，为基于功率潮流分析的电能计量新方法研究奠定了基础。在此基础上，利用小波分解重构算法对单个及复合非线性负载功率潮流进行分析，依据各功率潮流的物理意义及潮流方向，提出畸变信号条件下电能计量新方法。仿真结果表明采用基于功率潮流分析的电能计量新方法在理论上能够解决单个及复合非线性负载电能的合理计量问题，为研制畸变信号条件下电能计量仪表提供了理论依据。

1畸变信号条件下电网简化模型及功率的数学描述

本节在电网简化模型中对畸变信号条件下电压与电流分量进行定义，在此基础上对负载消耗的功率分量进行了定义。

1.1畸变信号条件下电网简化模型

畸变信号条件下电网的简化模型如图1所示，电网电源电压u(t)为正弦电压源，i(t)为电网电流，Zl为线路阻抗，Z为非线性负载阻抗，a点为负载电能计量节点。

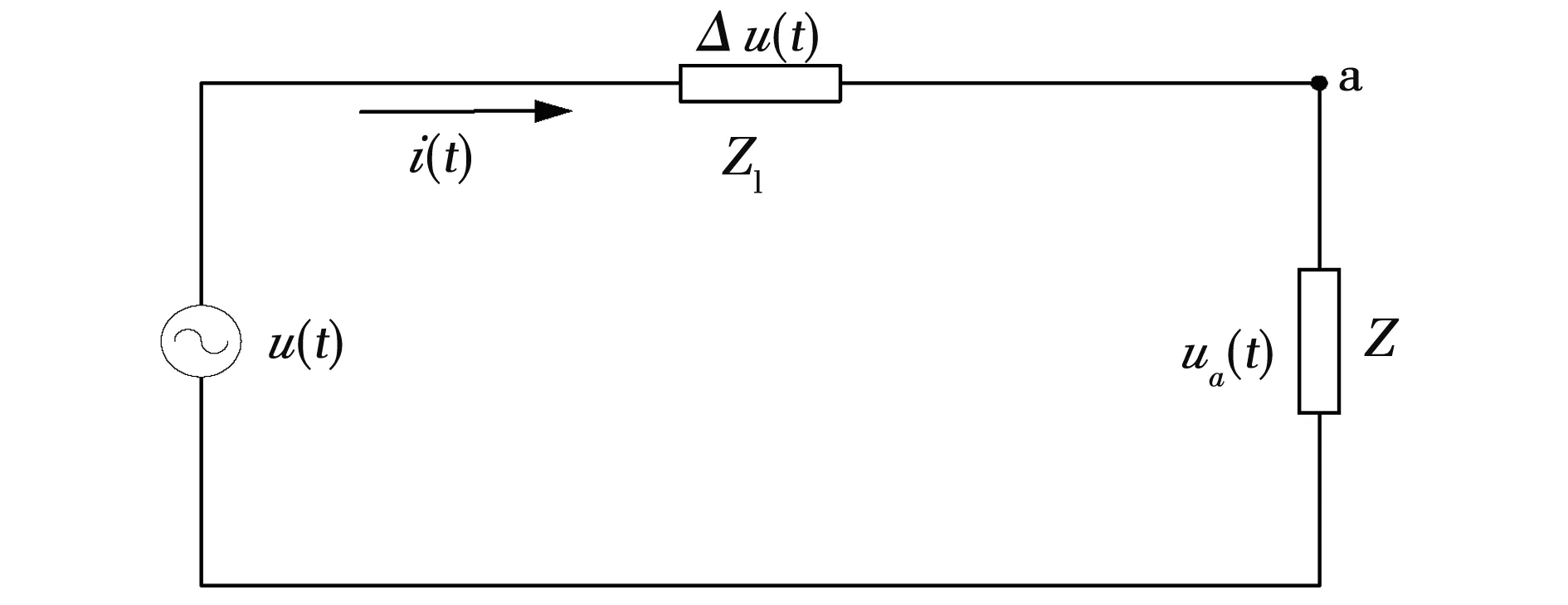
图1　电网的简化模型Fig.1　Simplified electrical network model

非线性负载电压与电流及其分解定义如下：

ua(t)=uI(t)+us(t),

(1)

i(t)=iI(t)+is(t)。

(2)

其中：uI(t)与iI(t)为基波分量；us(t)与is(t)为畸变分量。

线路阻抗压降可表示为

Δu(t)=ΔuI(t)+Δus(t)。

上式中，△uI(t)与△us(t)分别为线路阻抗压降中的基波电压与畸变电压。

在畸变信号条件下电网简化模型中，us(t)、is(t)与△us(t)均为随机畸变信号，它们不仅包括谐波分量，还包括直流、间谐波等其他形式的畸变分量。

1.2畸变信号条件下功率的数学描述

由功率理论可得a点的瞬时功率为

pa(t)=ua(t)i(t)。

(3)

将式(1)、式(2)代入式(3)得

pa(t)=[uI(t)+us(t)][iI(t)+is(t)]=

uI(t)iI(t)+uI(t)is(t)+us(t)iI(t)+

us(t)is(t)=

pI(t)+pIs(t)+psI(t)+ps(t)。

a点的平均功率为

PI+PIs+PsI+Ps。

式中：PI、PIs、PsI与Ps分别为非线性负载吸收的基波功率、基波电压与畸变电流产生的功率、畸变电压与基波电流产生的功率及畸变电压与畸变电流产生的功率。在此，称Ps为畸变功率。

2畸变信号条件下电网信号建模及小波分解算法

为了统一分析不同类型的单个及复合非线性负载的功率潮流及计量它们消耗的电能，需要建立满足电网实际情况的更具普遍性的非线性负载电流与电压模型。

由于Wiener泛函级数适合描述非线性系统，Wiener核的获取也相对较容易，所以首先求得非线性负载的Wiener核。但根据Wiener核展开的Wiener泛函级数是输入为高斯白噪声条件下的输出展开，而电网中负载的激励输入为正弦信号，所以依据Volterra泛函级数可以表示任何输入形式下输出的性质，将Wiener核转换为Volterra核，把正弦输入信号条件下的输出用Volterra泛函级数展开，得到正弦激励条件下负载输出电流与电压的数学模型。然后应用小波分解与重构算法分解出输出电流与电压的基波分量与畸变分量，为功率潮流分析打下基础。

2.1负载Wiener核的求取

由Wiener泛函级数性质可知负载Wiener核可以由下式表示

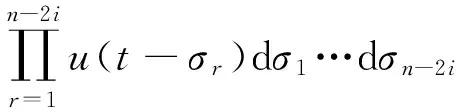
由上述理论可求得非线性负载的Wiener核[14]。

2.2Wiener核与Volterra核的转换

设一非线性系统由下述Wiener正交级数和Volterra泛函级数描述

y(t)=Gm[km(τ1…τm);x(t)]。

且E[Gn[kn;x(t+τ)]Gm[km;x(t)]]=0 ，对所有τ和m≠n。

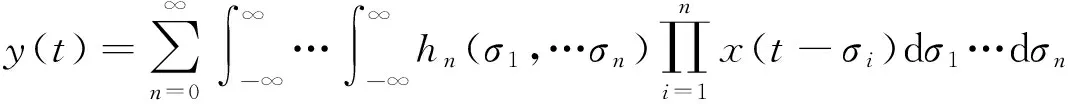
则可将N阶对称Volterra核具体表示为

通过上述转换关系可求得非线性负载的Volterra核[13]。

2.3基于Volterra泛函级数的负载输出电流模型

若已知非线性负载的Volterra核，则可求得任何输入信号下的输出。

负载输出电流信号Volterra泛函级数可以表示为：

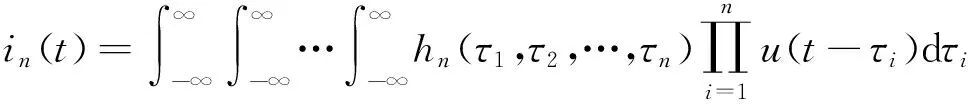
i(t)为系统输出；in(t)为系统的n阶输出；hn(τ1,τ2,…τn)为系统的n阶Volterra核；u(t-τi)为系统输入。

由图1，负载电压ua(t)由电流i(t)求得，即

ua(t)=u(t)-Rli(t)。

其中：u(t)为电压源；Rl为线路阻抗。

2.4小波分解算法

在负载输出电流与电压信号泛函级数模型的基础上，应用小波分解与重构算法可以求得功率潮流分析所需电流与电压的基波分量与畸变分量。

由多分辨率分析理论可知，u(t)、i(t)可分解成不同频率的成分，分别表示为：

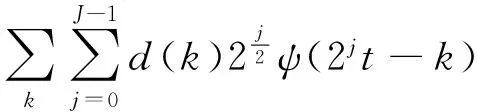
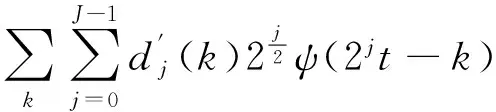
由双尺度方程可知：

其中h(k)、g(k)分别称为低通滤波器系数和高通滤波器系数，且满足

g(k)=(-1)kh(1-k)。

电压、电流的各频率成分的小波系数，可以表示成矩阵的形式：

同理，基波信号uI(t)、iI(t)的小波系数矩阵Cbasis、C′basic可分别表示如下：

因此，畸变信号us(t)、is(t)的小波系数矩阵Crand、C′rand可以分别表示为：

根据电网信号的具体情况，把不需要的小波系数置成零(比如噪声的小波系数等)，于是，得到重构畸变信号的小波系数矩阵

将上式带入重构方程得到畸变电压、电流

同样方法可重构出基波电压与电流分量。

3负载功率潮流仿真及误差分析

本节对电网中两种典型的非线性负载及它们组成的复合非线性负载进行功率潮流仿真分析与误差分析。

3.1半导体整流器功率潮流分析

半导体整流器的理论模型采用SIMULINK建模，仿真模型采用泛函级数建模。取采样频率fs=3 200 Hz，采样点数为n=256，采用Db40小波对输出电流i与电压u进行4层分解得到电流与电压的小波系数，根据低频的小波系数重构0-100 Hz的基波iI、uI分量；同理重构畸变分量is、us。

畸变电压与电流的小波分解如图2所示；仿真结果如表1所示。

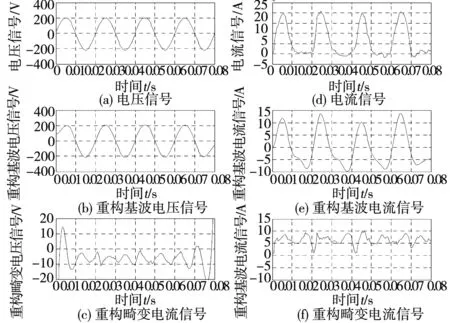
图2　半导体整流器件电流电压信号及分解Fig.2　　　　Current and voltage of Semiconductor rectifier　　　 and decomposition

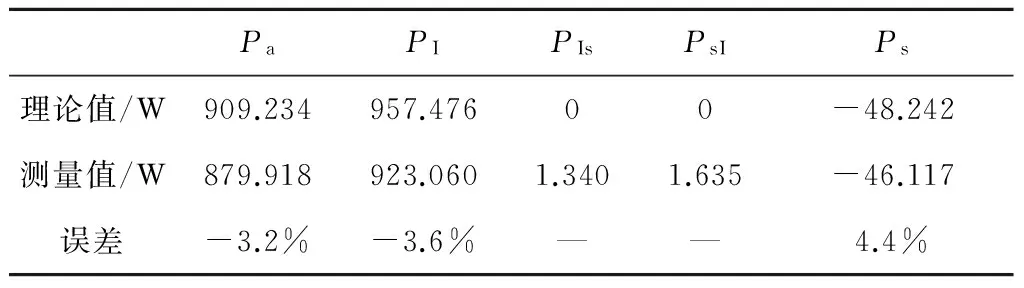
PaPIPIsPsIPs理论值/W909.234957.47600-48.242测量值/W879.918923.0601.3401.635-46.117误差-3.2%-3.6%——4.4%

由上述仿真结果可知：

1)功率测量准确度等级为10-2数量级，基波功率与畸变功率潮流方向与理论情况一致，说明所建泛函级数模型适用于半导体整流器这类谐波源功率潮流分析。

2)PIs和PsI均不为零，说明仿真模型和小波分析方法存在一定的误差，由此产生了仿真误差，但绝对误差很小，在实际应用中可以忽略。

3)在本仿真实例中，畸变功率占总功率的5.3%，但随着负载个数的增加其影响是不可忽略的。

3.2SS1型电力机车功率潮流分析

SS1型电力机车的理论模型采用SIMULINK建模[15]，仿真模型为泛函级数模型。取采样频率fs=3 200 Hz，采样点数为n=256，采用Db40小波对输出电流i与电压u进行4层分解得到电流与电压的小波系数，根据低频的小波系数重构0～100 Hz的基波iI、uI分量；同理重构畸变分量is、us。

畸变电流与电压的小波分解如图3所示；仿真结果及误差如表2。

由上述仿真结果可知：

1)功率测量准确度等级为10-2数量级，功率潮流方向仿真结果与理论情况一致，说明所建泛函级数模型适用于电力机车这类强时变的非线性负载功率潮流分析。

2)PIs和PsI均不为零，说明基波表忽略这两项既不合理也不准确。

3)在本仿真实例中，畸变功率Ps占总功率的2.8%，但随着负载个数的增加其影响也是不可忽略的。

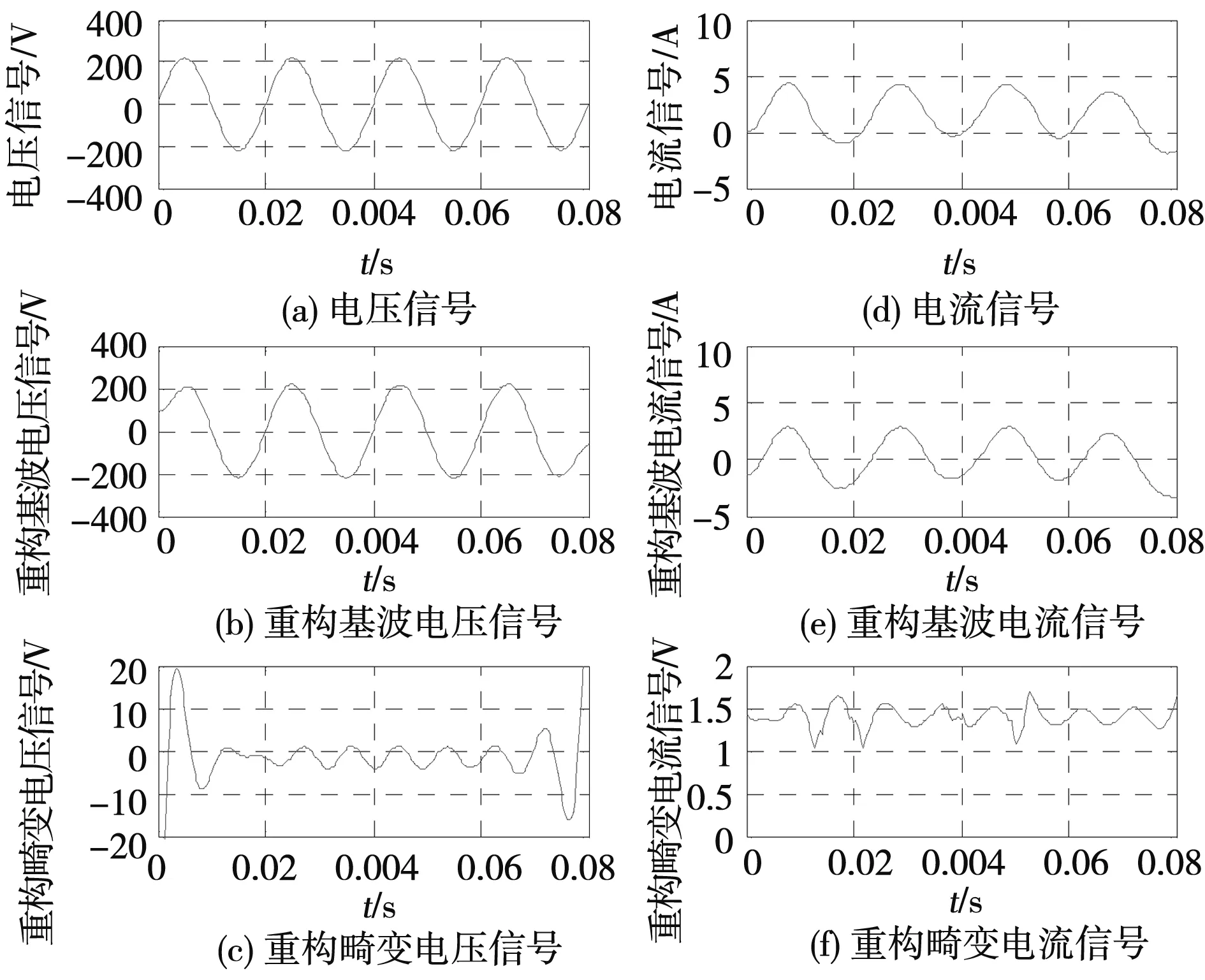
图3　SS1型电力机车负载电流电压及分解Fig.3　　　　Current and voltage of SS1 electric locomotive　　　and decomposition

PaPIPIsPsIPs理论值/W135.660139.1760.701-0.300-3.743测量值/W134.921138.0380.757-0.324-3.550误差/%-0.54-0.828.0-8.05.2

3.3复合系统功率潮流分析

复合系统理论模型由导通角α为π/4的半导体整流器件与SS1型电力机车负载按500∶1组成，仿真模型为泛函级数模型。取采样频率fs=3 200 Hz，采样点数为n=256，采用Db40小波对输出电流i与电压u进行4层分解得到电流与电压的小波系数，根据低频的小波系数重构0～100 Hz的基波iI、uI分量；同理重构畸变分量is、us。

畸变电压与电流的小波分解如图4所示；仿真结果与误差如表3所示。

由上述仿真结果可知：

1)复合系统测量准确度等级为10-2数量级，功率潮流方向仿真结果与理论情况一致，说明所建泛函级数模型适合于复合非线性负载功率潮流分析。

2)本仿真实例中，PIs和PsI均不为零，畸变功率占总功率的6.6%，说明随着负载个数增加，畸变总功率相应增加。

3)复合系统仿真误差与单个系统仿真误差为同一数量级，说明对复合系统统一进行功率潮流分析的可行性。

图4　复合型负载电压电流及其分解Fig.4　　　　Current and voltage of Composite Load　　　and decomposition

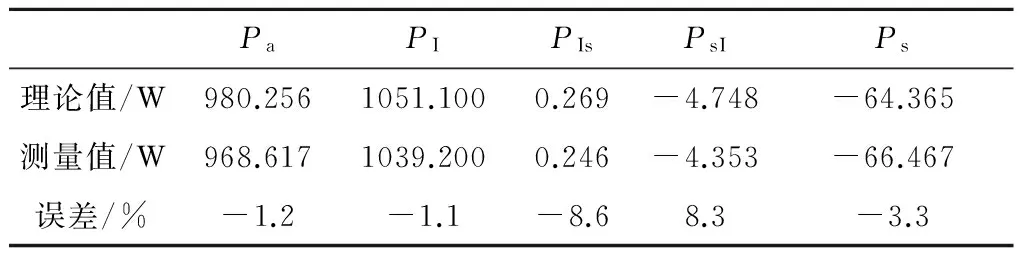
PaPIPIsPsIPs理论值/W980.2561051.1000.269-4.748-64.365测量值/W968.6171039.2000.246-4.353-66.467误差/%-1.2-1.1-8.68.3-3.3

3.4仿真误差分析

由以上仿真结果可见，单个及复合非线性负载各功率分量仿真值与理论值之间存在误差，经分析误差的主要原因有：

1)Wiener核的求取受计算机存储容量与计算速度、非理想的高斯白噪声与非最优的输入功率等级等因素影响，导致求取的Wiener核具有一定的误差。

2)由Wiener核求取Volterra核时，有限的Wiener核项数导致求得的Volterra核产生了误差。

3)由于理论模型为依据文献[14]应用SIMULINK建模，所以理论模型本身就有一定的误差，故也给仿真结果带来了误差。

4)采用Db40小波对电流与电压进行分解与重构的小波算法也存在误差，但由于小波算法准确度远远高于泛函模型的准确度，因此这项误差可以忽略不计。

4电能合理计量新方法

由上述3个仿真实验结果可知：

基波电压与基波电流产生的基波功率PI>0，这表明非线性负载从电网吸收基波功率PI，故该部分电能应计入负载消耗的总电能中。

基波电压与畸变电流产生的畸变功率PIs>0，这表明非线性负载从电网吸收畸变功率PIs，故应予以计量。

畸变电压与基波电流产生的畸变功率PsI<0，这表明该部分畸变功率没有被负载消耗，而是作为畸变功率回馈给电网。由于它是以基波电流的形式回馈给电网，不会给电网带来污染，所以应予以计量。

畸变电压与畸变电流产生的畸变功率Ps<0，这表明该畸变功率没有被负载所消耗，而是作为畸变功率回馈给电网，因为是以畸变电流的形式进行的，对电网造成污染，因此不予计量。

综上所述，基于功率潮流分析结果，所提出对非线性负载普遍适用的畸变信号条件下电能计量新方法：

P=PI+PIs+PsI，

P=Pa-PS。

其中：Pa为计量节点a处的实测功率，Ps为Pa中的畸变功率。

当us(t)、is(t)为高次谐波时，上式就变为

P=PI+PIs+PsI=PI。

按上式制造的电能表就退化为基波电能表，所以它也适用于谐波用户。

5结论

本文以非线性负载泛函级数模型为基础，对非线性负载进行功率潮流分析，依据功率潮流分析的结果，提出了畸变信号条件下电能计量新方法，并得到如下结论：

1)半导体整流器和电力机车以及它们组成的复合系统各功率分量仿真值与理论值存在误差，误差大小为10-2数量级。产生仿真误差的主要原因是应用泛函级数理论进行功率潮流分析的方法受计算机速度与存储空间的限制，一方面只能采用较少的采样数据进行计算，另一方面只能截取有限项来逼近实际系统。

2)半导体整流器和电力机车以及它们组成的复合负载各功率潮流方向(正负)仿真结果与理论结果一致，并且与文献[16]中针对特定非线性负载进行的功率潮流理论分析结果一致，说明由泛函级数理论统一分析负载功率潮流的方法是可行的，也说明基于功率潮流分析的电能计量新方法的正确性。

3)本文在泛函级数模型的基础上进行功率潮流分析，验证畸变信号条件下电能计量新方法的正确性，为解决电气参数及结构等未知的单个或复合非线性负载功率潮流分析及电能计量问题开辟了新的思路。

4)为了进一步验证电能计量新方法的普遍适用性，本文作者将研制畸变信号条件下电能计量实验仪，应用该实验仪能够对更多类型的非线性负载及其复合系统进行泛函级数建模及功率潮流实验分析，进一步验证畸变信号条件下电能计量新方法的正确性和普遍适用性。

参 考 文 献:

[1]李静，杨以涵，于文斌，等.电能计量系统发展综述[J].电力系统保护与控制，2009，37(11)：130-134.

LI Jing, YANG Yihan, YU Wenbin,et al. Review of electric energy metering system[J]. Power System Protection and Control,2009, 37(11)：130-134.

[2]邢颖，李宝树．非线性负荷对电网电压和电流的影响[J]．电气应用，2007，26(8)：25-28．

XING Ying, LI Shubao. The impact of nonlinear load on the voltage and current of the grid[J]. Electrotechnical Applycation, 2007，26(8)：25-28．

[3]刘骥，张明广，谢世强，等.混合有源电力滤波器的设计与仿真[J].哈尔滨理工大学学报，2010，15(05):22-26.

LIU Ji，ZHANG Mingguang，XIE Shiqiang,et al. Design and simulation on the hybrid active power filter[J].Journal of Harbin University of Science and Technology，2010，15(05):22-26.

[4]张晓冰，郑帅兵，车成弟，等.畸变信号条件下电能计量试验仪设计[J].哈尔滨理工大学学报，2015，20(05):74-79.

ZHANG Xiaobing，ZHENG Shuaibing，CHE Chengdi，et al. Design of electric energy measuring experimental apparatus on the condition of distorted signals[J].Journal of Harbin University of Science and Technology，2015，20(05):74-79.

[5]高笑，王步云，龙燕，等.电力谐波及其对电能计量的影响[J].后勤工程学院学报，2004(02)：53-55，73.

GAO Xiao, WANG Buyun, LONG Yan,et al. Electric harmonic and its influence on electric energy measurement[J]. Journal of Logistical Engineering University, 2004(02)：53-55，73.

[6]YUAN Haiwen，Qin Ye，Zhao Cheng，et al．Research on harmonic current distribution of Beijing’s rail traffic power supply system[C]// 9th International Conference on Electronic Measurement & Instruments．Beijing, China：The Chinese Institute of Electronics，2009：235-238．

[7]赵俊华，文福拴，杨爱民，等.电动汽车对电力系统的影响及其调度与控制问题[J].电力系统自动化，2011，35(14)：2-10,29.

ZHAO Junhua,WEN Fushuan,YANG Aimin，et al. Impacts of electric vehicles on power systems as well as the associated dispatching and control problem[J], Automation of Electric Power System, 2011, 35(14)：2-10,29.

[8]姚金雄，张涛，林榕，等.牵引供电系统负序电流和谐波电力系统的影响及其补偿措施[J].电网技术，2008：32(9)：61-64，88.

YAO Jinxiong,ZHANG Tao,LIN Rong,et al.Impacts of negative sequence current and harmonics in traction power supply system for electrified railway on power system and compensation measures[J].Power System Technology, 2008：32(9)：61-64, 88.

[9]严伟佳，蒋平，李峰．谐波对电能计量影响的研究[J]．华东电力，2006，34(2)：40-42．

YAN Weijia, JIANG Ping, LI Feng. Effects of harmonics on electric energy metering[J].East China Electric Power, 2006，34(2)：40-42．

[10]黄玉春.电力谐波对电能计量影响的分析与探讨[J].电力系统保护与控制，2009,37(10)：123-124,135.

HUANG Yuchun.Analysis and discussion of power harmonics influencing the electric energy computation[J].Power System Protection and Control, 2009,37(10)：123-124,135.

[11]金维宇，刘桂英.基于有源滤波器的基波电能表及其应用研究[J].长沙电力学院学报：自然科学版，2003，18(4)：41-44.

JIN Weiyu,LIU Guiying.Research on the fundamental electric energy meter based on active filter and its application[J]. Journal of Changsha University of Electric Power(natural science),2003，18(4)：41-44.

[12]滕召胜，罗志坤，孙传奇，等.基于小波包分解与重构算法的谐波电能计量[J].电工技术学报，2010,25(8)：200-206.

TENG Zhaosheng,LUO Zhikun, SUN Chuang qi,et al. Harmonic energy measurement based on wavelet packet decomposition and reconstruction algorithm[J].Transactions of China Electrotechnical Society,2010,25(8)：200-206.

[13]张晓冰，李云辉，房国志.非平稳畸变信号条件下电网信号建模[J].中国电机工程学报，2014，34(16)：2721-2728.

ZHANG Xiaobing, LI Yunhui,FANG Guozhi. Modeling for power grid signals under the condition of non-stationary distortion signals[J].Proceedings of the CSEE, 2014,34(16)：2721-2728.

[11]焦李成.非线性传递函数理论与应用[M].西安：西安电子科技大学出版社，1992：3-9，276-277.

[12]黄石柱，李建华，赵娟，等.基于MATLAB的电力机车数字仿真模型[J].电力系统自动化，2002，1(1)：51-55，60.

HUANG Shizhu, LI Jianhua, ZHAO Juan,et al. Matlab based digital simulation model for electrical locomotive[J]. Automation of Electric Power System, 2002，1(1)：51-55，60.

[13]张晓冰.畸变信号条件下电网功率潮流分析与电能计量新方法研究[D].哈尔滨：哈尔滨理工大学测控技术与通信工程学院，2007.15-31.

(编辑：贾志超)

XLPE电力电缆附件局部放电测量与分析赵学风1，蒲路1，琚泽立1，黄国强1，吕亮1，赵文炎2

(1.国网陕西省电力公司电力科学研究院，陕西 西安 710054；2.国网冀北唐山供电公司，河北 唐山 063000)

摘要:为研究XLPE电力电缆附件现场常见典型缺陷的放电特征，在3根电缆实体上分别设计制作了中间接头尖刺、主绝缘划伤和终端头应力锥错位3种放电模型，建立了基于PDBase的局部放电测量分析系统。对比研究了3种典型缺陷的局部放电特征，分析了放电次数相位分布谱图Hn(φ)、放电最大幅值相位分布谱图Hqmax(φ)和放电幅值分布谱图H(q)3种统计特征。试验结果表明，不同缺陷类型其放电发展过程不尽相同，呈现的PRPD谱图、单个脉冲波形、相位分布趋势及统计特征区别明显；而同一缺陷在相同条件下其放电特征呈现出相似规律且重复性好；这些特征为进一步开展电缆附件放电机理研究及放电类型的模式识别提供了有力的试验依据。

关键词:XLPE；典型缺陷；局部放电；PRPD谱图；脉冲波形；统计分析

蒲路(1976—)，男，博士，研究方向为电力电缆故障诊断及雷电监测技术；

琚泽立(1983—)，男，硕士，研究方向为配网设备带电检测技术；

黄国强(1971—)，男，硕士，研究方向为变压器故障诊断技术；

吕亮(1976—)，男，博士，研究方向为变压器故障诊断技术；

赵文炎(1985—)，男，硕士，研究方向为电力设备带电检测技术。

Measurement and analysis of partial discharge of XLPE power cable accessories

ZHAO Xue-feng1，PU Lu1,JU Ze-li1,HUANG Guo-qiang1，LÜ Liang1， ZHAO Wen-yan2

(1. State Grid Shanxi Electric Power Research Institute,Xi’an 710054,China;2. State Grid Jibei Tangshan Electric Power Supply Company,Tangshan 063000,China)

Abstract:In order to study the partial discharge (PD) characteristics of the typical defects in XLPE power cable accessories,three PD models as tip defect of middle joint,void defect in main insulation and dislocation of stress cone were designed on the cable entities,and then the PD measurement and analysis system based on the PDBase was established. The PD characteristics of three typical defects were detected and compared,and the statistical features ofHn(φ),Hqmax(φ) andH(q) were investigated. The experimental results indicate that it has the high stability and repeatability of the discharge on the identical defect model under the same condition. The discharge development process,PRPD patterns,time domain waveforms,central phase changing of PD signals and statistical features have very similar distribution characteristics and those of different defect has different ones. So it provides a test basis for the recognition of PD types and a deeper study of the PD mechanism of cable accessories.

Keywords:XLPE; typical defect; partial discharge; PRPD pattern; pulse waveform; statistical analysis

0引言

近年来，交联聚乙烯电力电缆(cross-linked polyethylene,XLPE)由于其质量轻、安装敷设容易、且具有良好的电气和耐热性能等优点被广泛应用于城市电网中[1-3]。然而，实际运行中的XLPE电力电缆由于受安装工艺、敷设环境、外力破坏、使用情况等因素影响，导致绝缘缺陷，乃至绝缘击穿事故不断发生，其中以电缆中间接头和终端头附件绝缘故障的比例为多[4-5]。

目前，国内采用预防性试验是保证电缆可靠运行的一个重要手段。然而，预防性试验存在试验周期长、停电试验结果不能准确反映运行状态下绝缘特征等缺点[6-7]。此外，电缆绝缘下降是一个逐步发展的过程，在故障发生早期，由于局部缺陷引起的放电信号非常微弱，传统的预防性试验项目很难检测到异常信号，因此，单一的传统试验方法已无法满足城市电网安全运行需求。

局部放电(partial discharge,PD)是电缆绝缘故障早期的主要表现形式，它既是引起绝缘劣化的主要原因之一，又是表征绝缘状况的主要特征量。运行经验和研究均表明：电力电缆局部放电量与绝缘状况密切相关，局部放电量的变化预示着电缆绝缘一定程度上隐患缺陷的存在，是定量分析绝缘劣化程度的有效方法之一[8-10]。因此，IEC、IEEE以及CIGRE等国际电力权威机构一致推荐PD试验作为XLPE电力电缆绝缘状况评价的最佳方法[11-13]。

本文以现场XLPE电力电缆附件中常见的典型缺陷为研究对象[14-17]，在三根YJLV22-8.7/10 kV、导体标称截面为3*95 mm2电缆实体设计制作了中间接头存在尖刺、主绝缘划伤以及终端应力锥错位三种缺陷试样；建立了基于脉冲电流法的局部放电检测系统，以及完善测量系统的抗干扰技术，对比研究了三种缺陷试样的局部放电特征，分析了局部放电次数相位分布谱图Hn(φ)、放电最大幅值相位分布谱图Hqmax(φ)和局部放电幅值分布谱图H(q)三种统计特征，为实现XLPE电力电缆有效的故障检测及分类提供了重要的试验依据。

1XLPE电力电缆附件缺陷

1.1缺陷设计

XLPE电力电缆在测试和运行期间，电缆本体、电缆中间接头、电缆终端接头的击穿概率依次递增。对于电缆本体，其中的缺陷是主绝缘内部的气隙、绝缘体和半导体存在的间隙以及半导体向绝缘中突出形成尖角等引起的缺陷；对于电缆中间接头和终端接头，其中的主要缺陷有橡胶和环氧分界面的缺陷、橡胶和XLPE分界面缺陷以及存在悬浮电极引发局部放电而造成的缺陷[12]。表1将XLPE电缆常见实际缺陷和试验放电类型进行了对应。

表1　实际缺陷和试验放电类型的对应关系

依据表1所描述的实际缺陷和试验放电类型的对应关系，选择其中三种缺陷分别在三根YJLV22-8.7/10 kV三芯实体电缆上设计加工，最终得到的缺陷试样如图1所示。

图1　缺陷试样Fig.1　Defect physical models

图1(a)为制作中间接头时未处理的尖刺缺陷。实际电缆附件安装过程中，由于安装工艺、安装人员技术水平等因素导致中间接头或终端头形成局部突起或尖端，工作电压下，突出尖端部分形成高场强区，导致局部放电的产生[13]。

图1(b)为中间接头制作过程中主绝缘划伤缺陷。当电缆中间接头或者终端制作过程中工艺不过关、制作流程不严谨等原因，常会划伤电缆主绝缘，而不被技术人员发现，最终变成气隙缺陷产生局部放电[10]。

图1(c)为电缆终端头制作过程中应力锥错位缺陷。终端制作过程中，因屏蔽层的剥除，导致屏蔽层末端电场发生畸变，为了改善电场分布情况，一般使用预制式应力锥来降低屏蔽层电场的畸变程度，使之电场分布均匀。现场安装应力锥对尺寸要求精准，对技术人员水平要求甚高。近年来，已发生多起因应力锥安装错位导致沿面放电，最终发生终端头爆炸的事故。因此，这里将应力锥错位缺陷作为现场发生的典型故障类型进行局部放电研究。

1.2PD测量系统

1)PD测量系统设计。如图2所示，为实验室内设计搭建的PD测量系统。图中U为220 V市电，T1、T2、T3分别为自耦调压器、隔离变压器、无局放高压试验变压器。T3额定电压为UN=100 kV，额定功率SN=10 kVA，100 kV以下放电量小于5 pC。水电组阻值为200 kΩ，用来限制试品击穿时流过的短路电流；耦合电容为100 pF；局放测量系统采用意大利产的TechImp PDBase系统，该系统可以记录放电PRPD谱图和单个放电脉冲波形，后处理软件具有信号特征提取、噪声干扰的剔除、专家系统识别及诊断等功能；此外，由于局放仪带宽有限，还采用一个50 Ω的宽带无感电阻作为测量阻抗，通过示波器(DPO4034，最高采样率达到2.5 GS/s，带宽为350 MHz)进行宽带局放脉冲波形的采集。为检验测量阻抗的频率响应特性，利用阶跃波信号的陡下降沿(为2 ns)作为输入信号，并与经测量阻抗后的响应输出信号进行比较，检验系统的原理图以及输出波形如图3所示。

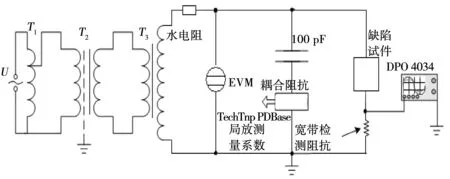
图2　测量系统图Fig.2　Measurement system

图3　测量阻抗校验Fig.3　Calibration of impedance measurements

2)测量系统的检验。为了进一步检验整个测量系统能否测量到准确的局放脉冲，实验室内利用电晕模型进行了测量，模型为标准针—半球模型，在针端施加高压，半球接地。单次脉冲测量结果及PRPD谱图如图4所示。测量结果的PRPD谱图和单个波形特征与国际上有关文献及教科书中描述的特性基本吻合[18-20]。

图4　电晕放电典型谱图及单个波形Fig.4　Typical PRPD and pulse of corona discharge

2局部放电测量及分析

2.1尖刺缺陷

1)PRPD谱图和单个放电波形。外加电压作用下，制作中间接头时残留的尖刺尖端处电场集中，形成高场强区，当电压达到尖端电晕起始电压时，尖刺开始出现电晕放电。图5、图6分别描述了随着外加电源电压的升高所测的电晕放电信号PRPD谱图变化趋势以及典型放电脉冲波形。

图5　尖刺放电PRPD谱图特征Fig.5　PRPD spectrum of tip discharge

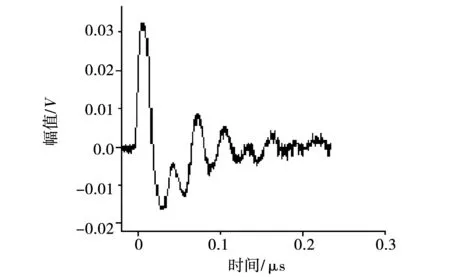
图6　单个放电脉冲Fig.6　Single discharge pulse

通过试验观察发现，尖刺电晕放电起始阶段，放电信号主要集中分布在电源相位的负半周，尤以峰值附近的放电最为强烈。根据图5不同电压作用下PRPD谱图的变化情况，金属尖刺缺陷的放电可以分为两个阶段：阶段Ⅰ为低电压下的初始放电阶段，如图5(a)所示，这时仅工频负半周出现少量放电脉冲而正半周基本没有放电。根据气体放电机理，尖刺正极性时，尖刺附近电离出的正离子质量较大，移动缓慢而电子则很快向尖刺移动，这样形成的反向电场削弱了尖刺场强，导致对应正半周不易发生放电；相反工频负半周时尖端为负极性，由于电子质量小移动速度快而迅速向地电位移动，正离子靠近尖端附近，增强了尖刺附近场强，从而容易先出现放电。此阶段放电量总体较小，谱图呈现“山丘”状；阶段Ⅱ为电压较高时放电快速发展阶段，如图5(b)所示。高电压下对应工频正半周气体电离强烈，大量正离子向板靠近等效减少了尖板间距，不断继续电离而形成电子崩进而形成流注放电，从而在正半周可能出现击穿产生幅值较大的放电脉冲。这样局部放电程度加剧，正半周也出现大量放电脉冲，而且正负半周放电脉冲均处于工频相位正、负峰值附近。

观察图6获得的单个放电波形可以看出，该波形为单峰脉冲，波头约为10 ns，脉冲持续时间200 ns左右，对应的包络线可视为单指数振荡衰减。

2)谱图统计特征。局部放电具有较强的随机性，为了进一步表征尖刺放电特点以及与其它缺陷进行对比分析，针对实验所得PRPD谱图，提取了3种表征放电统计特性的子谱图：局部放电次数相位分布Hn(φ)、放电最大幅值相位分布Hqmax(φ)和局部放电幅值分布H(q)，重点讨论负半周统计特征。

当外施电压为11 kV时，尖刺缺陷3种负半周统计特征如图7所示。由图可见，放电主要集中在工频负半周峰值相位附近，且峰值附近的放电幅值最高。图7(b)中左右孤立的柱形图为噪声点，因为这些相位窗内仅仅个别放电，且最大放电幅值和平均放电幅值无区别。对于中间接头尖刺缺陷，在整个加压过程中，放电基本以小幅值为主，如图7(c)所示，而对于放电幅值较大的部分，其放电次数很少，结合图5可知，小幅值的放电主要分布在负半周期，而大幅值的放电以正半周期分布居多。

2.2主绝缘划伤

1)PRPD谱图和单个放电波形。中间接头制作过程中主绝缘划伤造成的气隙缺陷在工频电压作用下，由于电压分布与介电常数成反比，气隙上承受的电场强度远大于XLPE绝缘介质，因此，气隙内部容易产生局部放电。图8为试验所获得气隙放电典型PRPD谱图变化。

图7　U=11 kV下尖刺放电谱图统计特征Fig.7　　　　Statistical characteristics of tip discharge　　　spectrum under U=11 kV

观察图8中不同电压下谱图变化可知，气隙试品起始放电阶段局部放电信号主要集中在工频电压过零点绝对值上升沿部分，随着电压的缓慢升高，放电幅值和放电密度增大，放电相位变宽，逐渐向峰值移动。总体来看，气隙放电的PRPD谱图在正半周期和负半周期近似呈对称现象，电压较低时，PRPD谱图呈现出“直三角”形状，随着外加电压的升高，谱图逐渐演变成“山丘”状。谱图形状以及发展变化与前述尖刺缺陷有很大区别，这有利于现场缺陷类型识别。

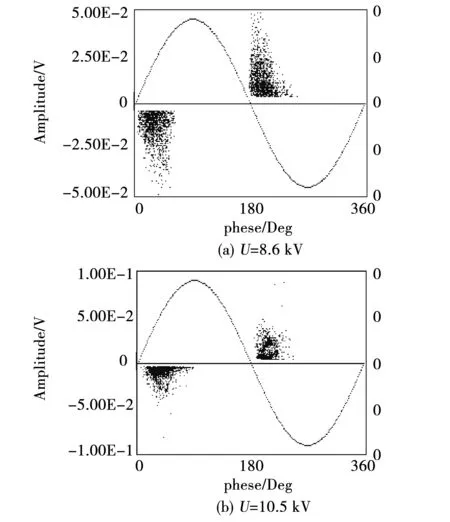
图8　气隙放电PRPD谱图特征Fig.8　PRPD spectrum of void discharge

试验捕获的气隙放电典型放电波形如图9所示。从图中可以看出，放电波形过冲幅值较大，振荡较尖刺缺陷下严重，波头时间约为几个ns，整个脉冲持续时间约为100 ns。对该放电信号进行频谱分析，得出能量主要集中在10 MHz之内。

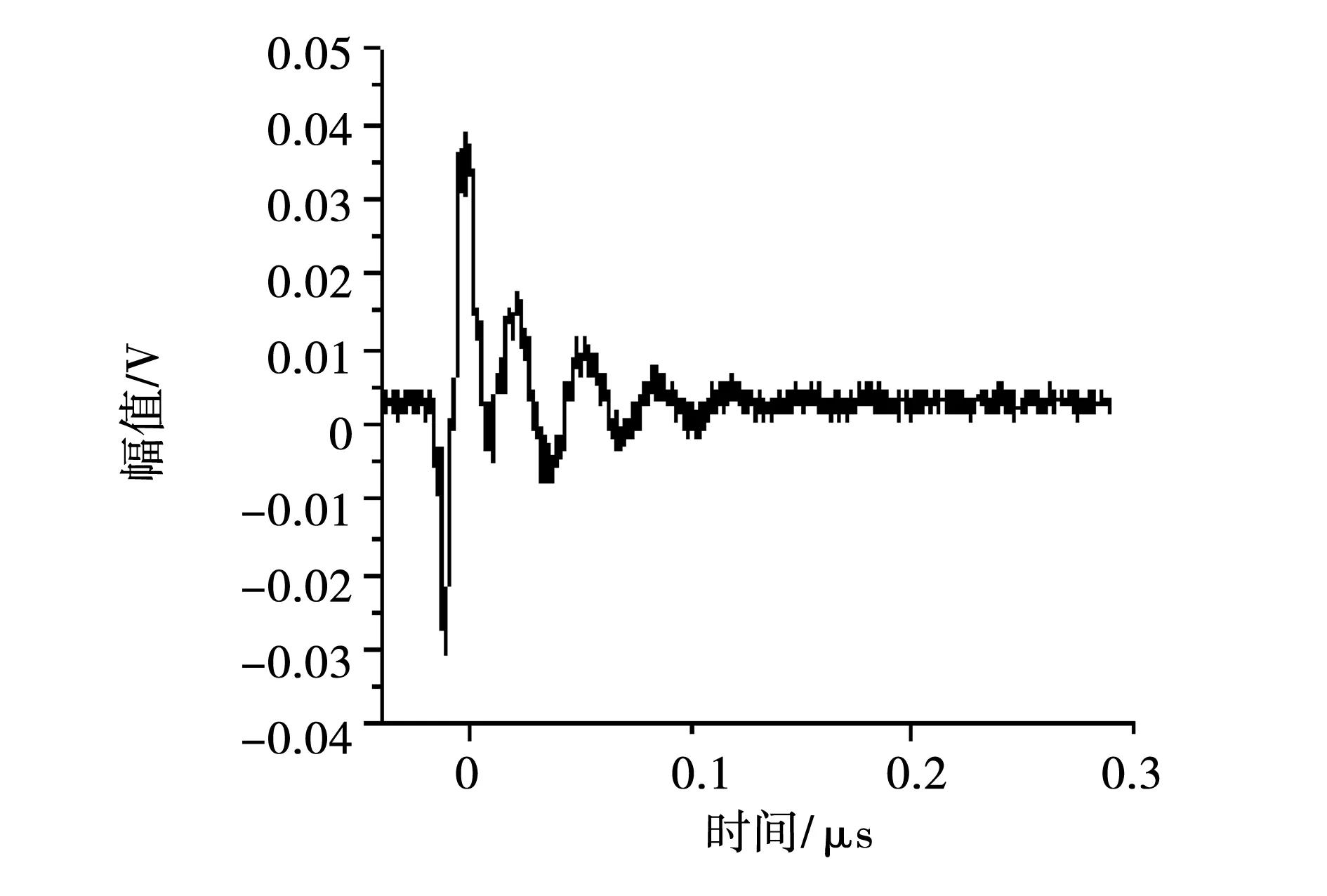
图9　单个放电脉冲Fig.9　Single discharge pulse

2)谱图统计特征。对于主绝缘划伤缺陷，外加电压达到12.1 kV时所得三种负半周统计特征如图10所示。由图可见，负半周放电集中分布在180～270°相位之间，放电次数最多的相位点为225°附近，正负半周期的放电较为对称，放电最大值也分布在225°附近；与尖刺缺陷比较可知，气隙一旦出现放电，放电幅值较大，现象更加剧烈。

图10　U=12.1 kV下气隙放电谱图统计特征Fig.10　　　　Statistical characteristics of void discharge　　　spectrum under U=12.1 kV

2.3应力锥错位

1)PRPD谱图和单个放电波形。电缆终端头应力锥安装错位导致试品不同外施电压下的局放PRPD谱图如图11所示。整个放电过程中谱图具有很明显的不对称性，即工频正半周的放电次数总是比负半周要大，且该趋势在整个实验过程保持不变。

根据PRPD谱图随电压的变化可以将局部放电的发展过程分为四个阶段：

图11　沿面放电PRPD谱图特征Fig.11　PRPD spectrum of surface discharge

①放电起始阶段。应力锥复合界面场强分布不均，当外加电压达到一定值时，复合界面产生微弱放电，谱图如图11(a)所示。初始放电发生在工频峰值处，即这个阶段是发生在外施场强最大值处，这个阶段的放电量很小，在数十到数百个PC之间。

②流注发展阶段。随着外加电压的升高，正负半周放电明显增多，正半周的放电次数远远多于负半周，且正半周的谱图形状从一个单峰的形式变化为双峰，正负半周的放电相位中心都向过零点偏移，如图11(b)所示。电压继续升高，放电进一步发展，正半周放电谱图双峰消失，转而变为“长条形”，几乎已经没有发生在外施电压峰值处的放电，负半周的放电有所增强，放电次数有所增加，如图11(c)所示。

③间歇击穿阶段。随着电压的升高，流注的发展距离越来越长，当流注达到地电极时，放电进入间歇击穿阶段，如同图11(d)所示。此时可以听到尖锐的间歇性放电声。这个阶段是临近闪络的临界阶段，流注虽然已经发展到了地电极，但没有足够高的电场驱动形成闪络。

④闪络阶段。当电场足够驱动流注到达地电极时，发生沿面闪络，实验中当电压升高到16 kV时，放电声越来越明显，也越来越密集，当继续升高电压至18.5 kV时，发生沿面闪络。发生闪络的瞬间可以听到较大的放电声。

外加电压9.5 kV下获得的沿面放电典型脉冲如图12所示。可以看出该波形对应的包络线可视为双指数振荡衰减波形，过冲幅值较之气隙放电小些，整个脉冲波形持续时间约为200 ns左右，波头时间约为十几个ns，经频谱分析，放电能量主要集中在5 MHz以下。

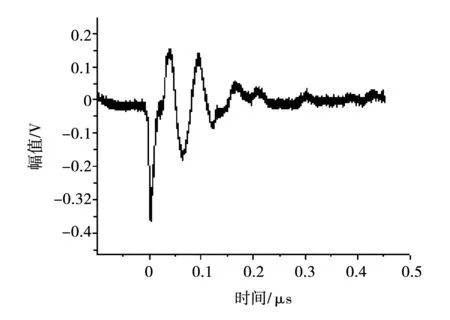
图12　单个放电脉冲Fig.12　Single discharge pulse

2)谱图统计特征。外加电压达到12.5 kV时应力锥错位缺陷所得三种负半周谱图统计特征如图13所示。由图可见，负半周放电集中分布在180～300°相位之间，放电次数及最大放电幅值在180～270°相位之间较之前两种缺陷分布比较均匀，与图11(c)所呈现的谱图形状一致；总之，与尖刺和主绝缘划伤缺陷相比，该缺陷放电起始电压最低，放电频率高，发展更容易。

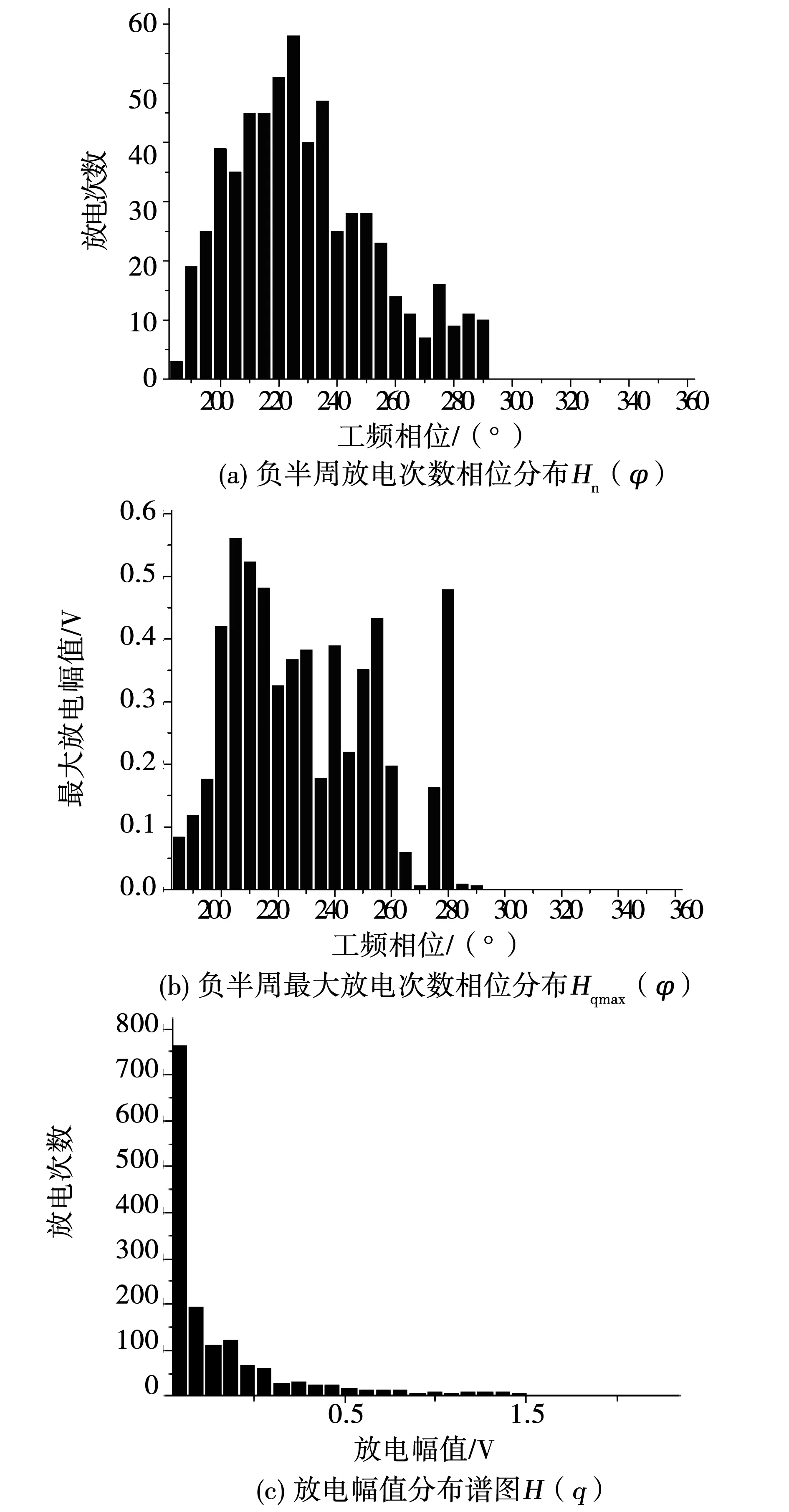
图13　U=12.5 kV下沿面放电谱图统计特征Fig.13　　　　Statistical characteristics of surface discharge　　　 spectrum under U=12.5 kV

3结论

本文针对现场XLPE电力电缆中间接头、终端头制作加工过程中常出现的故障类型(连接处尖端、主绝缘划伤、应力锥错位)，在10 kV三相XLPE电缆中间接头、终端头人工设置这些缺陷，研究了不同缺陷局部放电特征，得出结论如下：

1)中间接头尖刺缺陷随着外施电压的升高，其放电过程由低电压下的初始放电阶段和高电压下的快速发展阶段两个典型阶段组成，每个阶段正、负半周放电谱图特征、放电脉冲幅值、放电密度以及中心相位分布都存在明显区别；

2)主绝缘气隙缺陷起始放电阶段局部放电信号主要集中在工频电压过零点绝对值上升沿部分，随着电压的缓慢升高，放电幅值和放电密度增大，放电相位变宽，逐渐向峰值移动。总体来看，气隙放电的PRPD谱图在正半周期和负半周期近似呈对称现象；

3)终端应力锥错位缺陷与前两种缺陷相比，其放电起始电压最低，放电发展过程经历了典型的四个阶段：起始放电、流注发展、间隙击穿及沿面闪络阶段，每一阶段放电特征变化明显；

4)同一缺陷，其PRPD谱图、局部放电的脉冲波形及谱图统计特征随施加电压的变化呈现出相似的变化规律。此外，相同条件下，同一缺陷放电重复性好，这对于进一步开展XLPE局部放电机理研究提供了可靠的试验方法和平台；

5)不同缺陷类型其放电发展过程不尽相同，呈现的PRPD谱图、单个脉冲波形及谱图统计特征区别明显，对于现场缺陷类型及严重程度判别提供了可靠的试验依据。

[1]王伟．交联聚乙烯绝缘电力电缆技术基础[M]．西安：西北工业大学出版社，2011．

[2]王昌长，李福祺，高胜友．电力设备的在线监测与故障诊断[M]．北京：清华大学出版社，2006．

[3]杨连殿，朱俊栋. 振荡波电压在XLPE 电力电缆检测中的应用[J]. 高电压技术， 2006,3(32)： 27-30.

YANG Liandian,ZHU Jundong. Use of oscillating wave voltage in the measurements of XLPE power cable[J]. High Voltage Engineering,2006， 3(32):27-30.

[4]罗俊华. XLPE电力电缆绝缘特性试验方法的研究[D]. 西安：西安交通大学，2003.

[5]韦斌，王伟，李成榕，等．VHF钳型传感器在线检测110kV XLPE电缆局放[J]．高电压技术，2004，20(7)：37-39．

WEI Bin,WANG Wei,LI Chengrong,et al.Partial discharge on-Line detection of 110 kV XLPE cables using VHF clamp current transducer[J]. High Voltage Engineering,2004，20(7)：37-39．

[6]BOGGS S,DENSLEY J. Fundaments of partial discharge in the context of field cable testing [J]. IEEE Electrical Insulation Magazine,2000,16 (25): 13-18.[7]邱昌容，王乃庆．电工设备局部放电及其测试技术[M]．北京：机械工业出版社，1994．

[8]CAVALLINI A,MONTANARI G. C. A new methodology for the identification of PD in electrical apparatus: properties and applications [J]．IEEE Transactions on Dielectrics and Electrical Insulation，2005，12(2)：203-213．

[9]谢安生,郑晓泉等. XLPE 电缆绝缘中的电树枝结构及其生长特性 [J]. 高电压技术.2007,6(33):168-173.

XIE Ansheng,ZHENG Xiaoquan. Structures and propagation characteristics of electrical trees in XLPE cable insulation [J]. High Voltage Engineering,2007,6(33):168-173.

[10]MEIJER S,R A,JONGEN E,et al.VHF partial discharge detection during after -laying testing of power cables [C]//2007 International Conference on Solid Dielectrics,Winchester,U K,July 8-13,2007: 544-547.

[11]罗俊华,冯江,袁检等.交联聚乙烯电缆局部放电高频检测技术的研究[J]. 电网技术,2001 ,6(12): 42-45.

LUO Junhua,FENG Jiang,YUAN Jian,et.al. Study on detection of partial discharge in XLPE cable at higher frequency[J].Power System Technology,2001,25(12): 42-45.

[12]VAKILIAN M,BLACKBURN T R,JAMES R E,et al. Semiconducting layer as an attractive PD detection sensor of XLPE cables [J]. IEEE Transactions on Dielectrics and Electrical Insulation,2006,13(4): 885-891.

[13]DAKKA M,ABOU A,BULINSKI S.On-site diagnostic tests on polymer insulated cables using depolarization current measurement [C]//2007 International Conference on Solid Dielectrics,Winchester ,U K,July 8-13,2007: 725-728.

[14]姜芸，闵虹，夏荣，等．高压交联电缆接头局部放电的电容耦合法检测及分析[J]．高电压技术，2010，36(8):2005-2008．

JIANG Yun,MIN Hong,XIA Rong,et al.Capacitive coupling detection and characteristic analysis of partial discharge in high-voltage XLPE power cable joints[J]. High Voltage Engineering,2010,36(8):2005-2008.

[15]TOZZI M,CAVALLINI A,MONTANARI G C,et al. PD detection in ex-truded power cables: an approximate propagation model[J]. IEEE Transaction on Dielectrics and Electrical Insulation,2008,15(3):832-840.

[16]罗俊华，邱毓昌，杨黎明．10 kV及以上电力电缆运行故障统计分析[J]．高电压技术，2003,29(6):14-16.

LUOJunhua,QIU Yuchang,YANG Liming. Operation fault analysis of XLPE power cable above 10kV[J]. High Voltage Engineering,2003,29(6):14-16.

[17]常文治，李成榕，苏錡，等．电缆接头尖刺缺陷局部放电发展过程的研究[J]．中国电机工程学报，2013,33(7):192-201.

CHANG Wenzhi,LI Chengrong,SU Qi,et al. Study on development of partial discharge at the defect caused by a needle damage to a cable joint[J]. Proceedings of the CSEE,2013,33(7):192-201.

[18]CAVALLINI A,MONTANARI G C. A fuzzy logic algorithm to detect electrical trees in polymeric insulation systems[J]. IEEE Trans on Dielectrics and Electrical Insulation,2005,12(6): 1134-1144.

[19]CAVALLINI A,MONTANARI G C. PD inference for the early detection of electrical treeing in insulation systems[J]. IEEE Trans. on Dielectrics and Electrical Insulation,2004,11(4): 724-734.

[20]唐矩，龚宁涛，李伟，等．高压交联聚乙烯电缆附件局部放电特性分析[J]．重庆大学学报，2009，32(5): 528-534．

TANGJu，GONG Ningtao，LI Wei，et al．Characteristic analysis of partial discharge in high voltage XLPE cable accessories[J]．Journal of Chongqing University，2009,32(5)：528-534．

(编辑：贾志超)

Method of active power measurement under condition of distortion signal

ZHANG Xiao-bing，LI Yun-hui，CAO Wei

(College of Measurement and Communication, Harbin University of Science and Technology,Harbin 150080, China)

Keywords:electrical energy measurement; power flow; functional series; model of power load; wavelet transform

Abstract:For the problem of electrical energy measurement under the condition of non-stationary distortion signal, the power flow of the non-linear power load was analyzed based on the functional series models and a novel method of electrical energy measurement under the condition of distortion signal was presented. The Volterra kernel was calculated with Wiener kernel of non-linear power load on the conversion theorem of Wiener kernel and Volterra kernel. Then the output signal of sine input signal was expressed with Volterra functional series. The fundamental component and distortion component of current and voltage for power flow analysis was acquired with the decomposition and reconstruction of current and voltage signal using wavelet theory.The power flow analysis of non-linear power load was completed with the examples of semiconductor rectifiers,electric locomotives and their composition, following the IEEE-Std1459-2010 standard. A new method of power measurement under the condition of distortion signals is raised according to the physical meaning and flow direction of the electrical energy flow. The simulation results show consistency with theoretical result. This proves the new method based on the power flow analysis can implement the reasonable measurement of the electrical energy under the condition of distortion signal.

收稿日期:2014-10-16 2014-09-01

基金项目：国家自然科学基金(51277043) 国家杰出青年科学基金(51125029)；国家自然科学基金创新研究群体(51221005)

作者简介：张晓冰(1962—),女,博士,教授,研究方向为电气测量技术及仪器、现代信号处理； 李云辉(1987—),男,硕士研究生,研究方向为电气测量技术及仪器、现代信号处理； 赵学风(1983—)，女，博士，研究方向为电力电缆故障诊断技术；

通讯作者:张晓冰 赵学风

DOI:10.15938/j.emc.2016.06.011 10.15938/j.emc.2016.06.012

中图分类号:TM 933.3 TM 51

文献标志码:A A

文章编号:1007-449X(2016)06-0087-07 1007-449X(2016)06-0094-08

曹伟(1963—),男，教授，研究方向为电气测量技术及仪器、工业自动化仪表。