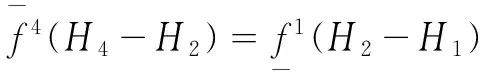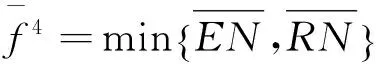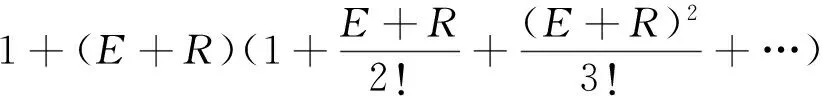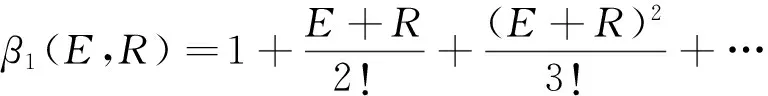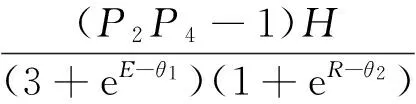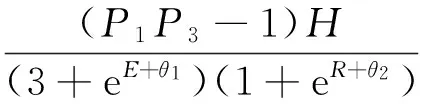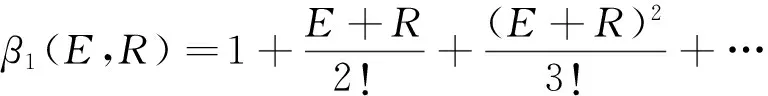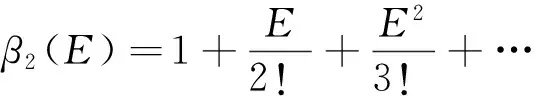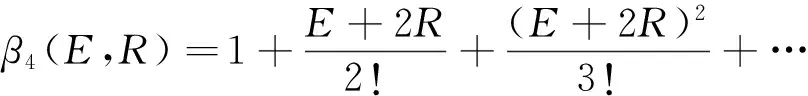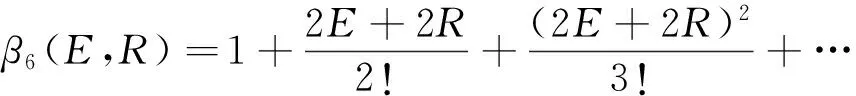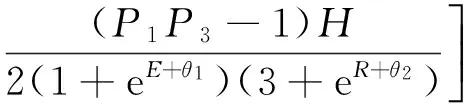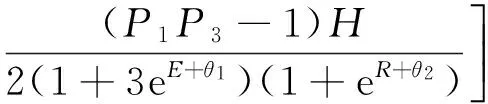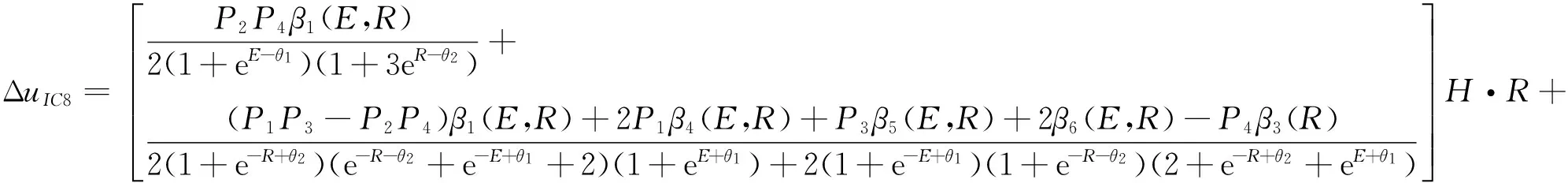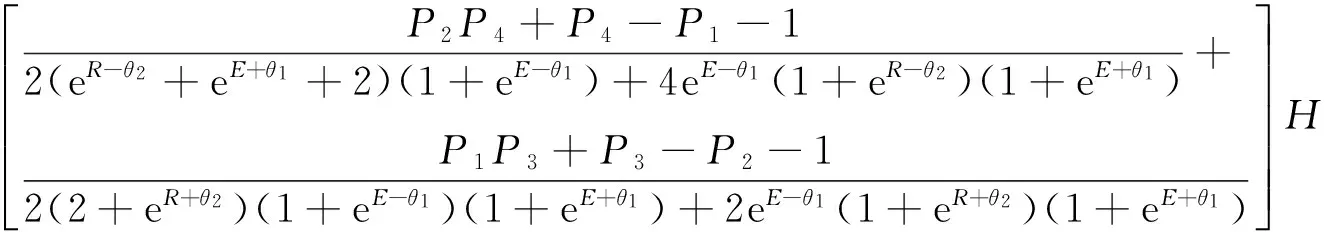区间二型模糊PI/PD控制器设计与结构分析

雷宾宾，　保宏，　许谦

(1.西安电子科技大学 电子装备结构设计教育部重点实验室，陕西 西安 710071；2.中国科学院 新疆天文台，新疆 乌鲁木齐 830011)



区间二型模糊PI/PD控制器设计与结构分析

雷宾宾1，保宏1，许谦2

(1.西安电子科技大学 电子装备结构设计教育部重点实验室，陕西 西安 710071；2.中国科学院 新疆天文台，新疆 乌鲁木齐 830011)

摘要:针对模糊控制器内部工作机理未知的问题，提出一种区间二型(IT2)模糊PI/PD控制器，并推导了该IT2模糊控制器的解析结构。该模糊控制器采用Mamdani型规则形式，为每个输入变量仅分配两个IT2模糊集合，具有规则数量少、规则不确定性影响小、控制输出平滑等优点。根据IT2模糊控制器的降型特点，将整个输入空间划分为15个分区，进而推导出在每个分区上控制输出的数学表达式，证明出该IT2模糊控制器等效为具有变增益的非线性比例积分(PI)或比例微分(PD)控制器。最后，在仿真和实验中与相对应的一型模糊控制器和传统PI控制器的控制效果进行对比，验证了该IT2模糊PI/PD控制器的有效性。

关键词:模糊控制；区间二型模糊集合；结构分析；变增益控制；非线性PID控制

0引言

在处理实际中的模糊规则不确定时，一型(T1)模糊控制器受到精确隶属度函数的限制。为克服这个局限，学者们提出了区间二型(IT2)模糊控制器。IT2模糊集合隶属度函数的“三维”特性和“宽带”效应，使得IT2模糊控制器在减少规则数量、平滑控制输出和优化控制响应性能等方面具有独特的优势[1-4]。近年来，IT2模糊控制器已经成为一个研究热点。

线性PID控制已经在工业过程中获得广泛地应用。然而由于线性PID控制在高度非线性、时变或大延时等复杂控制问题上表现的并不理想，学者们提出了非线性PID控制[5-7]。自上世纪80年代以来， T1模糊PID控制器一直受到学者们的关注并证明出是一种具有变增益的非线性PID控制[8-9]。随着IT2模糊控制的提出，考虑到它在处理系统不确定性方面的优势，文献[10]进而提出了一个IT2模糊PI/PD控制器，并通过数学推导证明该IT2模糊控制器等效为具有变增益的非线性PI/PD控制器。但是文献[10]提出的IT2模糊PI/PD控制器的上界隶属度函数(UMF)和下界隶属度函数(LMF)均为线性，这很大程度上限制了该模糊控制器在复杂控制问题上的表现。于是在文献[10]的基础上，文献[11]在设计IT2模糊PI/PD控制器时减少了对输入数量、模糊集合数量、模糊集合形状以及模糊规则后件等方面的约束条件，并证明出如果一个IT2模糊控制器的输入IT2模糊集合的UMF和LMF是分段线性或线性的，那么这个IT2模糊控制器可以等效为一个具有变增益的非线性PI/PD控制器同时附加一个随输入变化的余项。但是，之前的这些研究大都是针对具有线性或分段线性UMF和LMF的IT2模糊PI/PD控制器的设计和结构分析[10-12]，关于具有非线性UMF和LMF的IT2模糊PI/PD控制器的设计和结构分析方面的研究却很少涉及。

为此，本文提出了一个UMF和LMF均为非线性的IT2模糊PI/PD控制器。首先，该IT2模糊PI/PD控制器的设计采用Mamdani型规则形式，对称的规则后件，扎德与(AND)算子，Karnik-Mendel(KM)降型方法和重心解模糊法。其次，通过将该模糊控制器的输入空间划分为15个分区进行结构分析证明出它等效为具有变增益的非线性PI/PD控制器。最后，通过耦合水槽仿真算例[13]和工业机电整合驱动装置(IMDU)的正弦跟踪实验验证了该IT2模糊PI/PD控制器的有效性。

1IT2模糊控制器的配置

图1表示一个两输入单输出的IT2 模糊系统的结构图，图中IT2 模糊控制器的输入为

E(n)=Kee(n)=Ke(ref(n)-y(n)),

(1)

R(n)=Krr(n)=Kr(e(n)-e(n-1))。

(2)

其中：E(n)表示系统误差，简写为E；R(n)表示误差的变化速度，简写为R；y(n)是闭环系统的输出；ref(n)是参考信号；Ke和Kr是放缩参数。

IT2模糊控制器的输出信号为驱动控制信号的变化量，即

Δu(n)=f(E,R)。

(3)

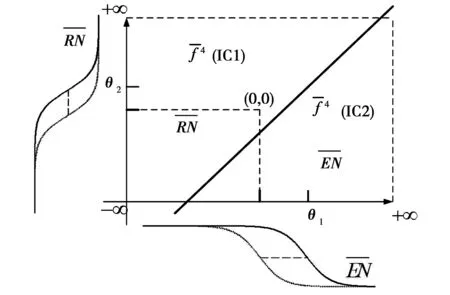
图1　IT2模糊控制系统结构图Fig.1　Structure diagram of IT2 fuzzy control system

(4)

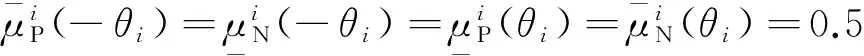
(5)

其中：x表示输入变量E或R，θi为设计参数，i=1,2。

输入变量E的UMF和LMF的表达式为

(6)

输入变量R的UMF和LMF的表达式为

(7)

其中θ1和θ2为设计参数。

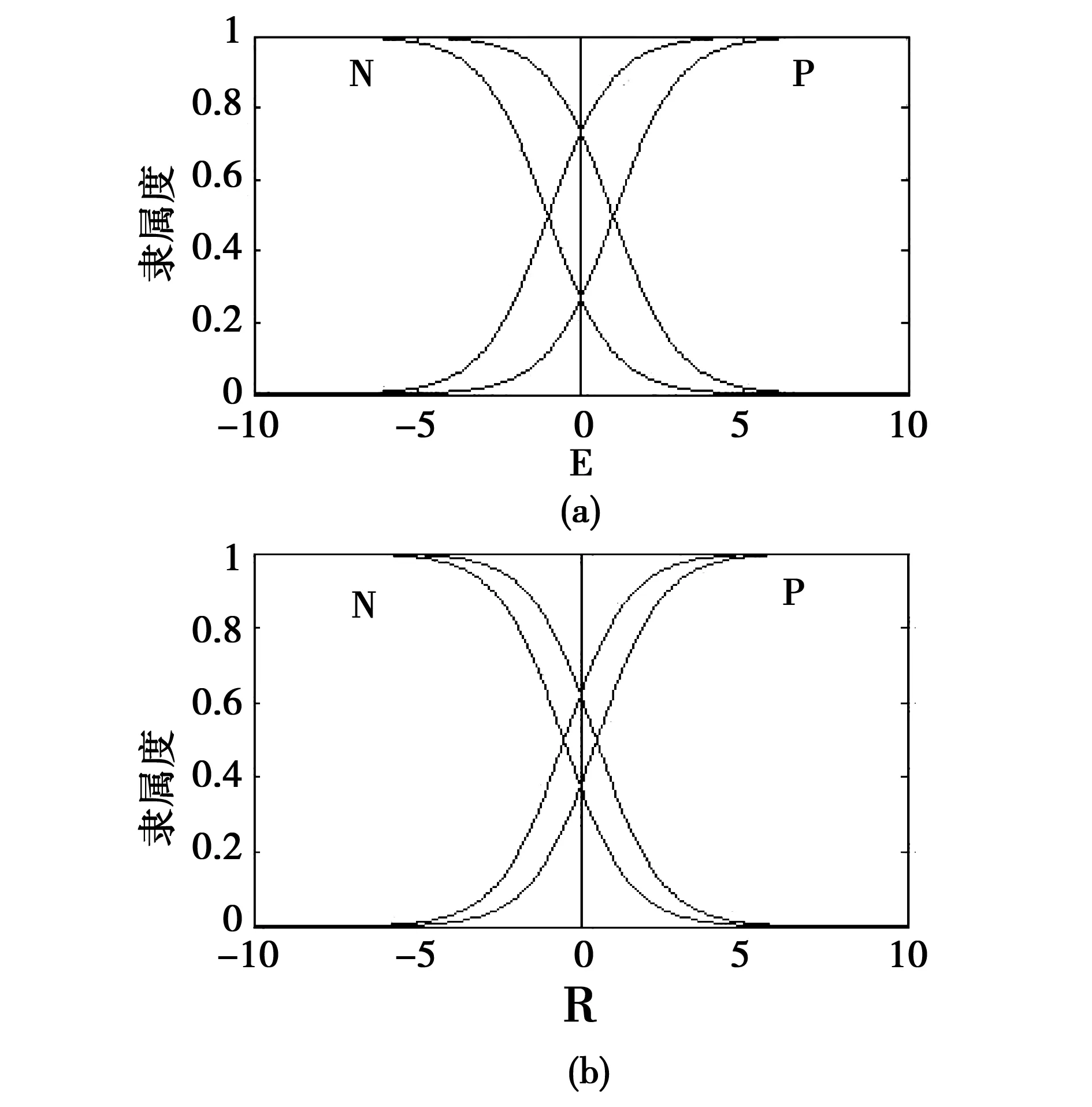
图2　输入变量E和R的模糊集合示意图Fig.2　Set diagram of fuzzy input variables

从图2中可以看出，选取的这种UMF和LMF均为非线性的IT2模糊集合的隶属度在系统误差E和系统误差的变化速度R在零点附近时表现敏感，而当E和R远离零点时IT2模糊集合的隶属度趋于饱和。这样的IT2模糊集合能够使得模糊控制器在理想位置附近的控制更加精细，有利于提高系统的控制精度。同时，UMF与LMF共同决定了IT2模糊集合的不确定迹的大小，因此，输入变量的模糊集合的不确定迹可以通过设计参数θ1和θ2来进行调节，而IT2模糊集合的不确定迹的大小，又直接影响着控制系统性能的优劣。

对于利用图2的IT2模糊集合对输入空间模糊化的模糊系统，通用的规则如下：

1)规则1：如果E(n)是正且R(n)是正，则Δu(n)为H1。

2)规则2：如果E(n)是正且R(n)是负，则Δu(n)为H2。

3)规则3：如果E(n)是负且R(n)是正，则Δu(n)为H3.

4)规则4：如果E(n)是负且R(n)是负，则Δu(n)为H4.

其中H1，H2，H3和H4是四个单点后件模糊集合。

采用扎德AND运算符，则上述每条规则的激活强度集合如下：

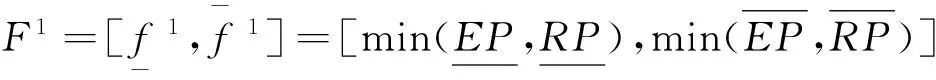
(8)

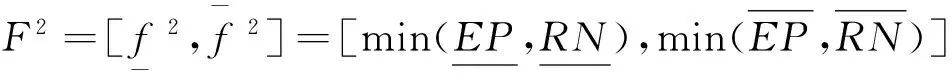
(9)

(10)

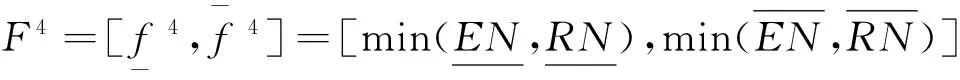
(11)

IT2模糊控制器利用KM降型方法。IT2模糊集合可以看作是许多嵌入的T1模糊集合的并集，因此IT2模糊集合的降型集合由所有嵌入的T1模糊集合的重心组成，则IT2模糊集合的降型集合就可以表示为Ycos=[yl,yr]。任一个嵌入的T1模糊集合的重心为

(12)

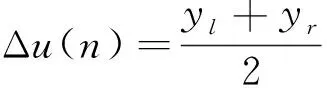
(13)

为了简化IT2模糊控制器的解析结构的推导过程，做出以下两点假设：

1)规则后件是对称的，即H2=H3；

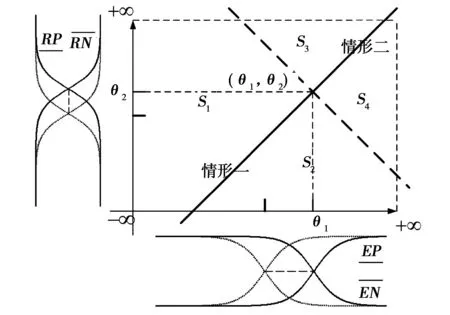
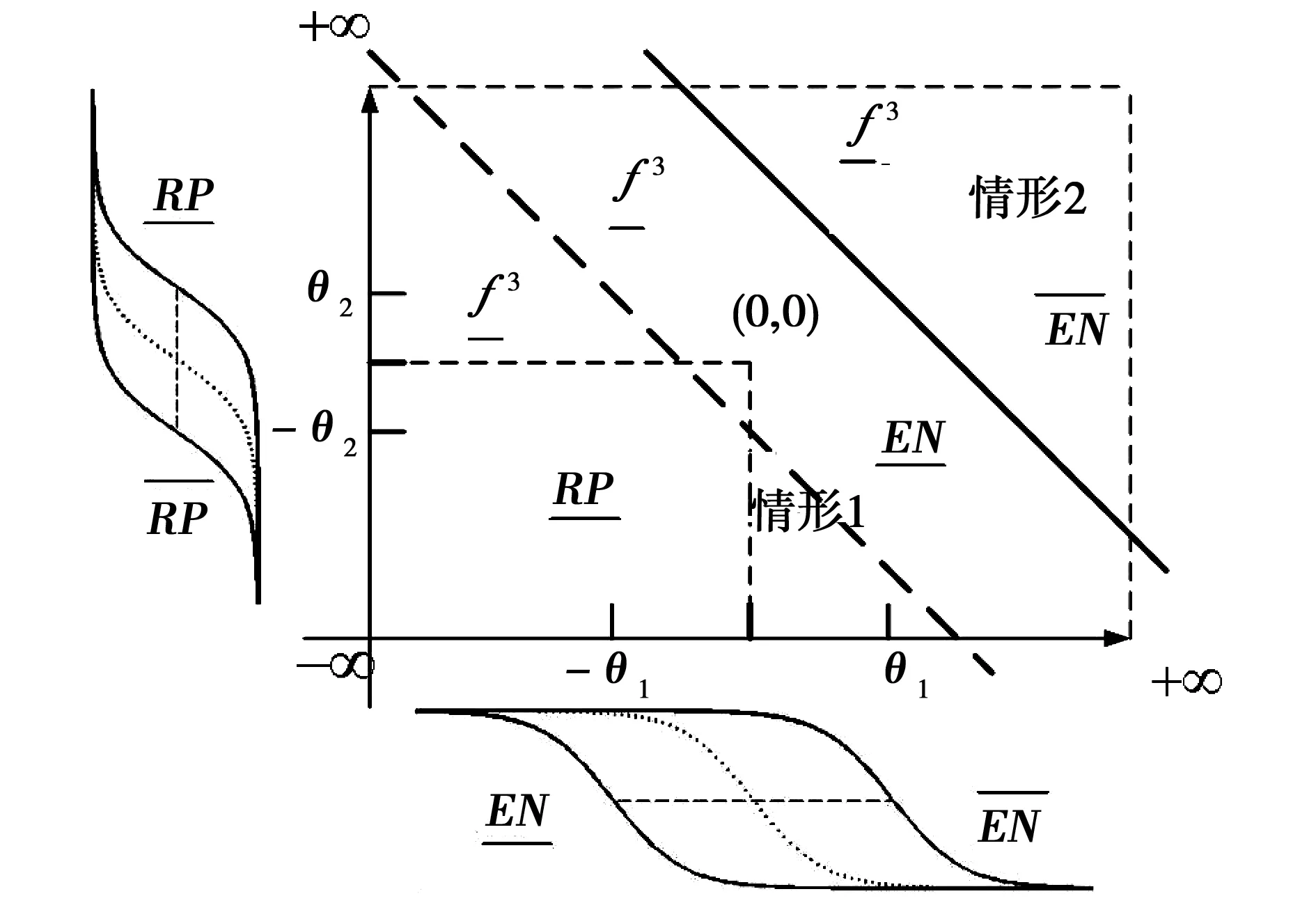
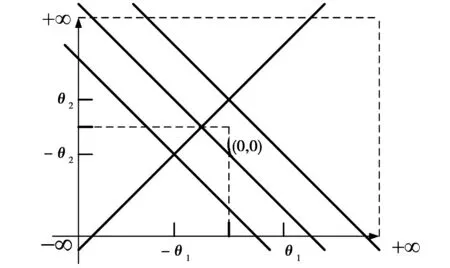
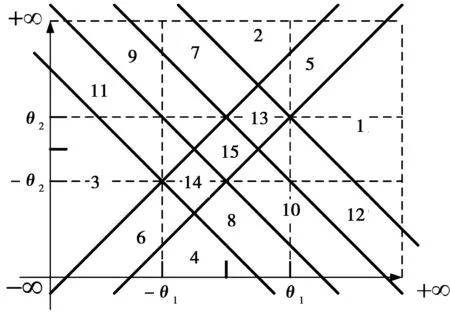
2)假定H4

2IT2模糊控制器的结构分析

2.1输入空间的分区

在上一章中假定四条规则的后件为H4

(14)

(15)

那么，用于确定转换点L和R的不等式表示：

HL≤yl

(16)

HR≤yr

(17)

由于转换点L和R必须满足上述不等式，因此L和R只能有两个可能值，即HL={H4,H3=H2}且HR={H4,H3=H2}。文中以降型集合左端点的计算为例，分为以下两种情形：

1)情形1。当H4≤yl≤H3=H2，即转换点L=4：

(18)

2)情形2。当H3=H2≤yl≤H1，即转换点L=2：

(19)

通过对比情形1和情形2中对应左端点的计算结果，可以得出如下特点：

1)规则1和规则4的规则后件对应的规则权重始终没有发生改变，即H1和H4对应的规则权重与开关点的位置无关。

2)在情形1中，H2=H3对应的规则激活强度为各自激活强度集合的下界，而在情形2中，H2=H3对应的规则激活强度为各自激活强度集合的上界，这说明了在开关点位置从H2=H3到H1的转换过程中，规则2和规则3的激活强度发生了改变，反之亦然，因此，假设有如下等式成立：

yl=yl1=yl2=H2=H3。

(20)

将式(16)及式(17)代入，可以得到：

H2=H3⟺

(21)

由于规则后件之间间隔相等，得

(22)

因此，情形1时应满足条件：

(23)

情形2时应满足条件：

(24)

下面以θ1>θ2的情况为例，通过以下步骤对输入空间分区：

图3　根据1的取值对输入空间的分区Fig.3　Partition by the value of1

图4　根据4的取值对输入空间的分区Fig.4　Partition by the value of4

图5　计算yl的情形划分示意图Fig.5　　　　Boundary (dash line) that divides the input　　　 space into two operating modes in yl

3)在不同的情形区域下，根据规则2和规则3对应激活强度的扎德AND运算结果对输入空间进行分区。

a)在情形1区域内，规则2和规则3的规则激活强度分别为各自规则激活强度集合的下界，即：

b)在情形2子区域内，规则2和规则3的规则激活强度分别为各自规则激活强度集合的上界，即：

图6　根据2和2的取值对输入空间的分区Fig.6　Partition of the input space by rule2

图7　根据3和3的取值对输入空间的分区Fig.7　Partition of the input space by rule 2

4)最后在考虑情形转换的前提下，在输入空间上叠加上述所有的分区，得到计算降型集合左端点时对输入空间的最终分区结果，如图8所示。类似地，在对yr计算表达式进行推导，采取上述相似的算法步骤，得到计算降型集合右端点时对输入空间的分区结果，如图9所示。最后叠加图8和图9，则得到IT2模糊PI控制器在输入空间上完整的分区结果，如图10所示。

图8　计算yl时对输入空间的分区Fig.8　Partition of the input space by the left endpoint yl

图9　计算yr时，对输入空间进行的分区Fig.9　　　　Partition of the input space by the right　　　endpoint yr

图10　　　　当θ1>θ2时，IT2模糊PI控制器最终　　　分区结果Fig.10　Partition of the input space

2.2每个分区上IT2模糊控制器输入输出表达式的推导

在这一节中，将式(14)和式(15)中的规则激活强度替换为各自对应的具体表达式，进而推导该IT2 模糊控制器在每个分区上的输入输出数学关系表达式。下面以IC1区为例详细介绍IT2 模糊控制器的解析结构的推导过程。

1)IC1区。将式中的规则激活强度替换为相对应的关于模糊输入变量的函数表达式，从而得到：

(25)

下面，将eE+R进行麦克劳林展开:

(26)

为便于IT2模糊PI控制器的增量输出表达式的推导，首先作如下假定：

P1=eθ1,P2=e-θ1,P3=eθ2,P4=e-θ2。

(27)

(28)

通过上述假设可以得到：

(29)

同理，对yr进行相似的推导过程，从而得到IC1子区域内降型集合右端点的表达式：

(30)

最后，IC1分区上IT2模糊PI控制器的增量输出表达式：

(31)

其他分区上IT2模糊PI控制器的增量输出表达式的推导过程与IC1区相似。为便于每个分区上IT2模糊PI控制器的增量输出的表达，首先对每个分区统一作如下假定：

P1=eθ1,P2=e-θ1,P3=eθ2,P4=e-θ2,

(32)

(33)

(34)

(35)

(36)

(37)

(38)

那么，在上述假设的基础上可以得到其余所有子区域内的IT2模糊PI控制器的增量输出表达式。

2)IC2区。

(39)

3)IC3区。

(40)

4)IC4区。

(41)

5)IC5区。

(42)

6)IC6区。

(43)

7)IC7区。

(44)

8)IC8区。

(45)

9)IC9区。

(46)

10)IC10区。

(47)

11)IC11区。

(48)

12)IC12区。

(49)

13)IC13区。

(50)

14)IC14区。

(51)

15)IC15区。

(52)

通过对比IT2 模糊控制器在每个分区上推导得到的输入输出数学关系表达式和传统PID控制器的增量表达形式，可以证明得到文中提及的IT2 模糊控制器等效为一个非线性变增益的PI控制器。同理，如果图 1的IT2 模糊控制器的输出信号直接为控制信号，则根据PID控制器的位置表达形式可以得到文中提及的IT2 模糊控制器等效为一个非线性变增益的PD控制器。因此，所提出的IT2 模糊控制器等效为一个具有变增益的非线性PI或者PD控制器。

3仿真与实验

3.1仿真

仿真对象是一个耦合水槽，如图 11所示。对耦合水槽建模[13]如下：

(53)

图11　耦合水槽模型示意Fig.11　Schematic diagram of the coupled tank model

分别利用PI控制器、IT2模糊控制器和相对应的T1 模糊控制器控制1号水槽的注水量，使得2号水槽液面达到期望高度。模型具体的参数取值如下：H1=H2=0，α1=α2=5.618 6，α3=10，Q2=0，目标液面高度取15 cm。则得到三种控制器的仿真结果如图 12和图 13，控制效果的各项指标见表格 1，表格中选取系统误差绝对值与控制时间乘积的积分(ITAE)作为性能指标用于反映整体控制效果，如式(54)。ITAE指标值越大，系统控制性能越恶劣。

(54)

其中T表示仿真截止时间。

图12　三种控制器的阶跃响应对比图及局部放大图Fig.12　Step responses of PI, T1 and IT2 controller

图13　误差和误差变化速度轨迹Fig.13　Trajectory of error and rate

系统类型上升时间/s超调量/%调节时间/sITAEPI307.50961057946.4T1304.6289936747.6IT2302.4333735927.9

通过图12和表1可以看出，与对应的T1模糊控制器和PI控制器相比较，IT2模糊控制器在保证不增加上升时间的情况下，明显地减小了超调量和调节时间。从而说明本文提出的IT2模糊PI/PD控制器能够有效地优化控制响应性能。

图13绘制了误差信号和误差变化速度分别在PI控制器、T1模糊控制器和IT2模糊控制器控制下的变化轨迹。从图中可以看到，在误差接近零时IT2模糊控制器能够使系统误差获得更快的收敛。

3.2实验

IMDU是一台工业机电整合驱动装置，如图14所示。该仪器既可以做基本的伺服系统，反向补偿，摩擦力补偿以及工业系统的高阶系统的耦合。该装置的方面上配有四个轴，其中的两个是电机驱动，而另外两个是自由旋转.所有四个轴都装有光学编码器.电机是由具有100瓦功率的线性控制放大器所驱动。

图14　IMDU实物图Fig.14　Physical map of IMDU

在系统输出添加均匀白噪声，并对IMDU的一个驱动轴在负载状态下进行角位置正弦跟踪控制实验，同时利用正弦跟踪曲线的绝对误差的积分(IAE)作为性能评判标准，对T1 模糊控制器和IT2 模糊控制器的控制性能进行比较，具体参数选取如下：Ke=200，Kr=0.5，H=25，θ1=0.25,θ2=0.4。负载状态下，T1模糊系统和IT2模糊系统正弦跟踪曲线和正弦跟踪误差曲线如图15和图15所示。

通过图15和图16可以看到，由于系统输出添加的白噪声，T1模糊系统在一个正弦周期内的跟踪曲线的IAE达到3 381.4，然而IT2模糊系统在一个正弦周期内的跟踪曲线的IAE仅为1 769.3，控制性能提高了47.7%，从而充分说明了本文提出的IT2模糊PI/PD控制器在处理系统扰动方面要胜过相应的T1模糊PI/PD控制器。

图15　T1和IT2 模糊系统的正弦跟踪曲线Fig.15　Sine tracking curve of T1 and IT2 fuzzy system

图16　T1和IT2模糊系统的正弦跟踪误差曲线Fig.16　　　　Sine tracking error curve of T1 and IT2　　　fuzzy system

4结论

本文提出的IT2模糊PI/PD控制器主要有以下几个特点：

1)该IT2模糊控制器仅产生四条模糊规则，模糊推理简单，同时避免了对隶属度函数的依赖性。

2)IT2模糊集合的“带宽”特性能够应对微分信号在实际应用中引起的内部干扰，因此该IT2 模糊PI/PD控制器在工业控制中具有广阔的应用前景。

3)通过对输入空间上15个分区的结构分析证明出该IT2模糊控制器等效于具有变增益的非线性PI/PD控制器。

参 考 文 献:

[1]DU X，YING H. Control performance comparison between a type-2 fuzzy controller and a comparable conventional Mamdani fuzzy controller[C]//NAFIPS 2007-2007 Annual Meeting of the North American Fuzzy Information Processing Society, San Diego, CA, 2007:100-105.

[2]HAGRAS H. Type-2 FLCs: A new generation of fuzzy controllers[J].IEEE Computational Intelligence Magazine, 2007, 2(1): 30-43.

[3]MENDEL J M. Type-2 fuzzy sets and systems: an overview[J].IEEE Computational Intelligence Magazine, 2007, 2(1): 20-29.

[4]潘永平, 黄道平, 孙宗海. II型模糊控制综述[J]. 控制理论与应用, 2011, 28(1):13-23.

PAN Yongping, HUANG Daoping,SUN Zonghai. Overview of type-2 fuzzy logic control[J], Control Theory and Applications, 2011, 28(1):13-23.

[5]HUANG H, HAN J Q. Nonlinear PID controller and its applications in power plants[C]//IEEE International Conference on Power System Technology, 2002, 3:1513-1517.

[6]JIANG F, GAO Z. An application of nonlinear PID control to a class of truck ABS problems[C]//IEEE Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, 2001, 1:516-521.

[7]谢先平, 王旭东,吴晓刚,等. 自动离合器位置跟踪神经元自适应PID控制[J]. 电机与控制学报, 2008, 12(5):555-560.

XIE Xianping, WANG Xudong, WU Xiaogang, et al. Neuron adaptive PID control for position tracking control of automatic cluth[J]. Electric Machines and Control, 2008, 12(5): 555-560.

[8]YING H, Siler W, Buckley J J. Fuzzy control theory: A nonlinear case[J], Automatica, 1990, 26: 513-520.

[9]李庆春, 沈德耀. 一种PID模糊控制器(fuzzy PI + fuzzy PD型)[J]. 控制与决策, 2009, 24(7):1037-1042.

LI Qingchun, SHEN Deyao. Brand-new PID fuzzy controller (fuzzy PI + fuzzy PD)[J]. Control and Decision, 2009, 24(7):1037-1042.

[10]DU X, YING H. Derivation and analysis of the analytical structures of the interval Type-2 fuzzy PI and PD controllers[J], IEEE Transactions on Fuzzy Systems,2010, 18: 802-814.

[11]ZHOU H B, YING H. A method for deriving the analytical structure of a broad class of thpical interval type-2 mamdani fuzzy controllers[J], IEEE Transactions on Fuzzy Systems,2014, 21(3): 447-458.

[12]NIE M W, TAN W W. Analytical Structure and Characteristics of Symmetric Karnik-Mendel Type-Reduced Interval Type-2 Fuzzy PI and PD Controllers[J].IEEE Transactions on Fuzzy Systems,2012, 20(3): 416-430.

[13]WU D, TAN W W. A simplified type-2 fuzzy controller for real-time control[J], ISA Trans., 2007, 45(4):503-516.

[14]Amin H A,YING H. Strucural analysis of fuzzy controllers with nonlinear input fuzzy sets in relation to nonlinear PID control with variable gains[J]. Automatica, 2004, 40:1551-1559.

(编辑：刘素菊)

Design and structural analysis of interval Type-2 fuzzy PI/PD controller

LEI Bin-bin1,BAO Hong1,XU Qian2

(1.Key Lab. of Electronic Equipment Structure Design, Ministry of Education, Xidian University, Xi’an 710071,China;2.Xinjiang Observatory, National Astromomical Observatories, Chinese Academy of Sciences, Urumqi 830011, China)

Abstract:Aiming at the problem of unknown internal working mechanism for the fuzzy controller, a class of interval type-2 (IT2) fuzzy PI/PD controller was proposed, and the analytical structure of this IT2 fuzzy controller was derived.Mamdani rule form was used in fuzzy controller and each input variable only has two IT2 fuzzy sets. The fuzzy controller has the advantages of fewer rules, smaller uncertainty effects of fuzzy rules and smoothing control output. The proposed IT2 fuzzy controller is proved to be equivalent to a nonlinear proportional integral (PI) or proportional differential (PD) controller with variable gains by dividing the input space into 15 partitions and calculating the mathematical expression of the control signal on each partition. Finally, the effectiveness of the IT2 fuzzy controller were verified by comparing the control effects with its type-1 fuzzy controller and traditional PI controller in the simulation and experiment.

Keywords:Fuzzy control; Interval type-2 fuzzy set; structural analysis; variable gain control; nonlinear PID control

收稿日期:2015-03-28

基金项目：新疆维吾尔自治区重点实验室专项(2014KL012);973计划项目(2015CB857100);上海航天科技创新基金(SAST201413);中央高校基本业务费(SPSY021401);国家自然科学基金(51490660；51305321)

作者简介：雷宾宾(1992—)，男，博士研究生，研究方向为模糊控制、半实物仿真；

通讯作者:保宏

DOI:10.15938/j.emc.2016.06.007

中图分类号:TP 273

文献标志码:A

文章编号:1007-449X(2016)06-0050-13

保宏(1971—)，男，博士，教授，博士生导师，研究方向为结构协同设计、精密控制等；

许谦(1981—)，男，高级工程师，研究方向为大口径天线及系统。