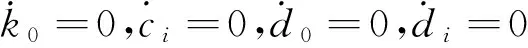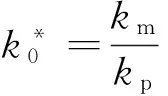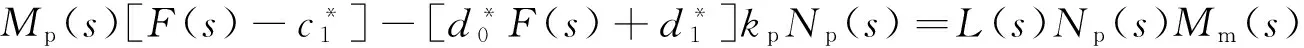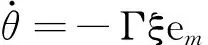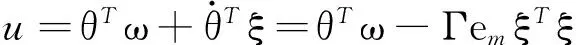平面开关磁阻电机模型参考自适应位置控制

曹广忠，　黄苏丹，　汪济欢，　段吉安，　钱清泉

(1.深圳大学 深圳电磁控制重点实验室，广东 深圳 518060;2.西南交通大学 电气工程学院，四川 成都 610031;3.中南大学 高性能复杂制造国家重点实验室，湖南 长沙 410083 )



平面开关磁阻电机模型参考自适应位置控制

曹广忠1，黄苏丹2，汪济欢1，段吉安3，钱清泉2

(1.深圳大学 深圳电磁控制重点实验室，广东 深圳 518060;2.西南交通大学 电气工程学院，四川 成都 610031;3.中南大学 高性能复杂制造国家重点实验室，湖南 长沙 410083 )

摘要:为了提高平面开关磁阻电机的位置精确度，研究一种基于模型参考自适应控制理论的平面开关磁阻电机控制方法。采用最小二乘法辨识了平面开关磁阻电机的线性化模型参数，根据李亚普若夫稳定性理论，以力指令为控制量并采用输入输出变量设计了平面开关磁阻电机模型参考自适应位置控制器，基于dSPACE半实物实时仿真系统，构建了实时在线控制实验平台，进行了平面开关磁阻电机的模型参考自适应位置控制实验。研究表明：基于模型参考自适应控制的平面开关磁阻电机系统能平稳、准确地跟随给定位置，提高了电机位置精确度，验证了提出的平面开关磁阻电机模型参考自适应控制方法的可行性和有效性。

关键词:平面开关磁阻电机；定位精确度；模型参考自适应控制；李亚普若夫稳定性理论；位置控制

0引言

现代精密、超精密加工装备对高精确度的平面驱动有着迫切的需求[1-4]，如光刻机是集成电路等微电子产业中最重要、最复杂的设备，其执行机构主要由超精密平面驱动装置实现[1,5]。传统平面驱动装置由两套旋转电机配合齿轮、丝杆等中间机械转换机构相互垂直组合而成。由于齿轮、丝杆等直线运动转换装置存在侧隙、变形等一系列问题，从而导致传统平面驱动装置的精确度较低，难以满足高精确度应用需求[6]。直驱式平面开关磁阻电机摒弃了齿轮、丝杆等机械传动部件，直接利用电能产生平面运动，消除传动过程的位置误差，具有结构简单、安装方便、精确度高、成本低、可靠性高及可在恶劣环境下运行等优点，在机械加工、电子产品生产、半导体IC制造、制造自动化仪表设备等精密加工领域展现出极大的应用前景[7-9]。但平面开关磁阻电机的非线性磁路、力脉动以及无缓冲机械转换装置，使平面开关磁阻电机的高精确度位置控制成为难点[10]。

迄今，平面开关磁阻电机控制方法的研究已初见成效。文献[9]详细地讨论了平面开关磁阻电机的理论基础、结构优化设计、电磁特性分析及其控制系统的设计，但并没有给出电机高精确度位置控制方案；文献[11]和[12]分别将自抗扰控制器和鲁棒控制器引入平面开关磁阻电机系统，增强了系统鲁棒性，改善了电机性能，但未给出电机位置精确度；文献[13]通过采用具有遗传因子的最小二乘法实时在线辨识系统参数，利用极点配置算法调整电机的控制量，提高了平面开关磁阻电机的位置精确度，但未给出电机的位置精确度指标；文献[3]采用了内环为电流环，外环为位置环的级联双环PD控制器，并利用二维查找表的方式克服由磁路非线性引起的力-电流-位置之间的非线性关系，将电机的位置精确度提升至5 μm，但是，对于不同运行情况下的PD控制器，需要对PD参数进行相应的调整，同时产生较大的噪声[11]。因此，平面开关磁阻电机能否获得微纳级的位置精确度，为超精密加工装备提供高精确度平面驱动技术的支撑，需要探索新的控制方法。

本文提出了一种基于模型参考自适应控制理论的平面开关磁阻电机位置控制方法。该控制方法无须预先明确平面开关磁阻电机精确的数学模型，比较被控对象与参考模型的输出从而获取自适应控制误差，用以驱动自适应调节器。通过在线连续调整控制器参数，使电机位置跟随参考位置[14]。该控制方法为平面开关磁阻电机高精确度位置控制提供新思路。本文给出平面开关磁阻电机的结构与数学模型，辨识平面开关磁阻电机线性化模型参数，设计平面开关磁阻电机模型参考自适应位置控制器，搭建实验平台，进行实验验证，并给出研究结论。

1平面开关磁阻电机结构与数学模型

1.1平面开关磁阻电机结构

与旋转开关磁阻电机类似，平面开关磁阻电机遵循磁阻最小原理，即励磁磁通总是按磁阻最小的路径闭合，可以将其形象地理解成将两个旋转开关磁阻电机分别沿径向剖开，在正交的X轴和Y轴分别按圆周展开成直线，X轴和Y轴的两套励磁绕组相互垂直交替地被嵌在动子平台上。研制的改进型平面开关磁阻电机样机如图1所示[15-17]。

图1　平面开关磁阻电机样机Fig.1　Prototype of the PSRM

电机主要由定子阵列、X和Y轴动子绕组、位移传感器(光栅尺)、直线导轨等部分组成。其中定子块如图2(a)所示，4个定子块首尾拼接组成一个定子单元，如图2(b)所示。多个定子单元排列成定子阵列，如图2(c)所示，所有定子阵列固定在定子机座上，根据实际需要可以很方便地组合成任意尺寸的定子平面。动子平台由6个动子绕组组成，3个沿X轴横向摆放的绕组负责Y轴方向的运动，另外3个沿Y轴纵向摆放的绕组负责X轴方向的运动，6个绕组垂直交替排列，通过两套直线导轨支撑动子平台在X和Y轴上的运动。位移传感器用于测量电机动子平台位置。平面开关磁阻电机主要参数如表1所示。

图2　平面开关磁阻电机的定子结构Fig.2　Structure of the stator of the PSRM

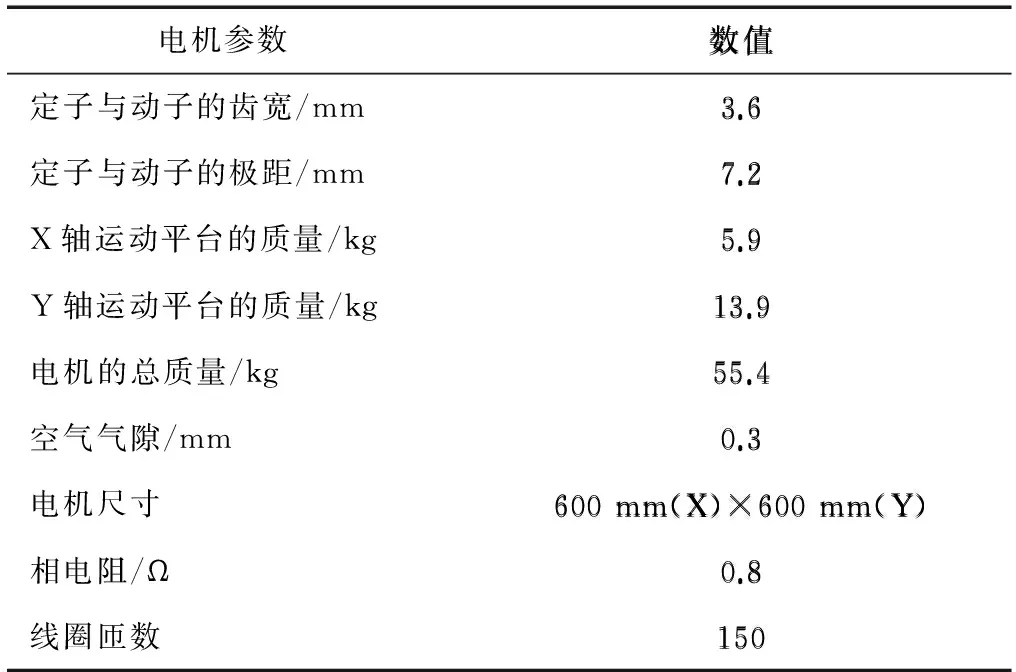
数值3.67.25.913.955.40.3600mm(X)×600mm(Y)0.8150电机参数 数值定子与动子的齿宽/mm3.6定子与动子的极距/mm7.2X轴运动平台的质量/kg5.9Y轴运动平台的质量/kg13.9电机的总质量/kg55.4空气气隙/mm0.3电机尺寸600mm(X)×600mm(Y)相电阻/Ω0.8线圈匝数150

1.2平面开关磁阻电机运动耦合分析与控制框架

当平面开关磁阻电机YA相动子绕组输入幅值为3 V频率为50 Hz的正弦电压时，其它相各动子绕组的感应电压如图3所示。由图3可知，各相动子绕组中最大感应电压为YA相动子励磁电压的0.67%，因此，动子绕组间互感效应可忽略不计，电机在X、Y轴两个方向上的运动相互解耦，可实现两个方向的解耦控制。

平面开关磁阻电机两个方向的运动解耦，可等效成两台相互垂直运行的直线电机，且每个轴的控制方式相同，故只对电机一个方向的运动进行分析。平面开关磁阻电机X轴方向的位置控制框图如图4所示。给定位置yr经过自适应控制器后输出力指令u，再通过力分配函数将力指令分配到每一相绕组中得到三相动子的力指令fxa、fxb、fxc，最后将力指令转化为对应的电流指令ixa、ixb、ixc控制电机的运行。利用力分配函数，采用两项励磁通电的方案可有效减小电机力脉动[9]。

1.3平面开关磁阻电机数学模型

产生正交推力的平面开关磁阻电机线圈绕组垂直交替排布，相间解耦，绕组间互感可忽略，电机l轴第k相励磁绕组的电压平衡方程可表示为

图3　动子绕组的感应电压Fig.3　　　　Induced voltages of the phase windings　　　 of the mover

图4　平面开关磁阻电机X轴的位置控制框图Fig.4　　　　Position control block diagram for the X-axis　　　 of the PRSM

(1)

其中，

ψlk(ilk(t),sl(t))=L(sl(t),ilk(t))ilk(t)。

(2)

不考虑电机磁路饱和，将式(2)带入式(1)，有

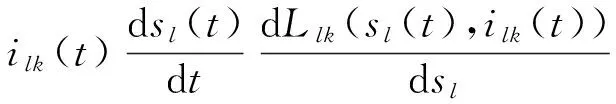
l=X,Y; k=A,B,C。

(3)

式中:Ulk，ilk，Rlk，Llk和ψlk分别为电机l轴第k相绕组的端电压、相电流、相电阻、相电感和总磁链；sl为电机l轴定子与动子的相对位置；右端第1项为单相回路的电阻压降；第2项是由电流变化引起磁链变化而感应的电动势；第3项是由动子平台位置改变引起绕组中磁链变化而感应的电动势。

电机在两个方向上的运动是解耦的，当l轴运动时，根据牛顿力学定律，运动方程可表示为

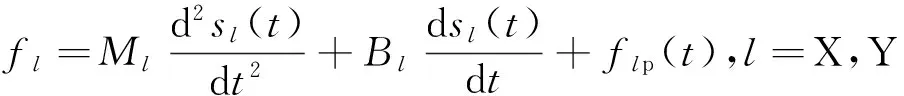
(4)

式中：Ml为电机l轴运动平台的质量，Bl为阻尼系数，fl为电机产生的电磁推力，flp为负载或外部扰动。根据式(4)，以力指令为输入、电机位置为输出的系统传递函数可近似表示为

(5)

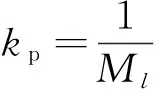
定义电机l轴第k相的磁共能为

Wlo=∫ψlkdilk=∫ilkdψlk。

(6)

假设在线性磁场下，根据磁共能推导电机l轴的推力为

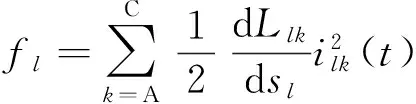
(7)

根据式(7)可以计算力电流转换函数为

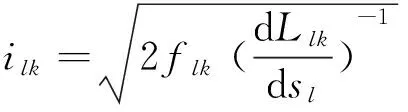
(8)

图5为实验测量的平面开关磁阻电机力-电流-位置三维特性曲线，该曲线表明力-电流-位置之间呈强非线性关系，但对电机建模时一般采用式(7)的线性磁场下的线性模型。

电机系统在运行时，存在各种环境噪声和干扰，定义u(k)为系统输入，y(k)为系统输出，ζ(k)为外部扰动，则式(4)所描述的二阶系统的离散形式可以表示为

A(z-1)y(k)=B(z-1)u(k)+ζ(k)。

(9)

式中:

(10)

2平面开关磁阻电机模型参考自适应控制

2.1平面开关磁阻电机系统参数辨识

给定模型参考自适应控制虽然能够通过自适应控制率的在线调整使系统达到稳定，但是由于系统物理的可实现性，可调参数的初值选取问题会影响系统进入稳定状态的快速性，甚至会影响系统的稳定性。为了选取合适的可调参数初值，采用最小二乘法辨识平面开关磁阻电机系统的模型参数。

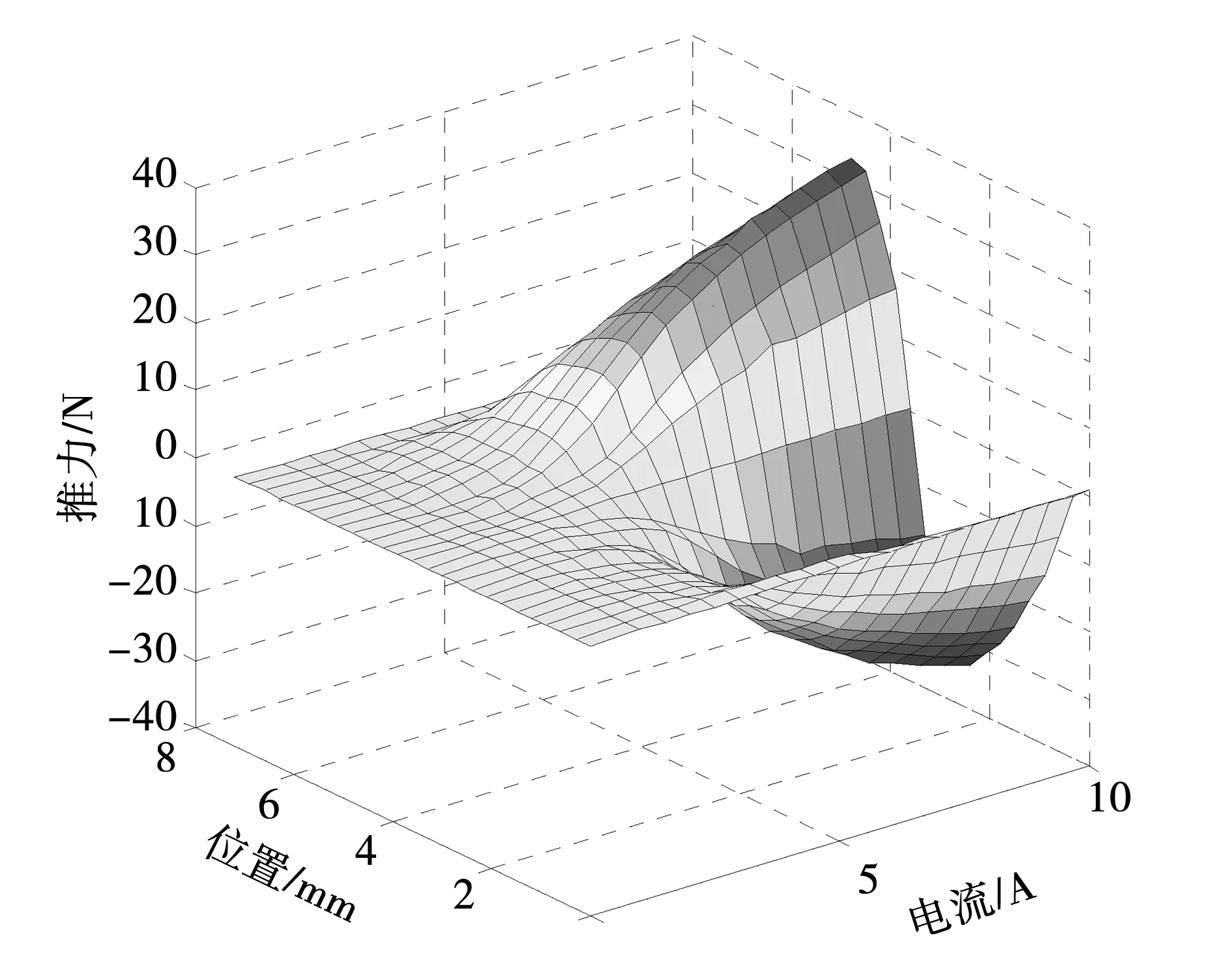
图5　平面开关磁阻电机力-电流-位置三维特性曲线Fig.5　　　　Three-dimensional curve of the current,　　　position,and force

将式(9)写成最小二乘形式为

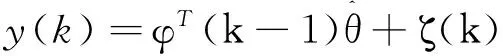
(11)

(12)

(13)

2.2平面开关磁阻电机模型参考自适应控制器设计

根据式(5)可知，平面开关磁阻电机系统是一个相对阶为2的系统，利用系统输入输出量，根据Lyapunov 稳定性理论设计出如图6所示的平面开关磁阻电机模型参考自适应控制系统。

Wp为被控对象，即平面开关磁阻电机，Wm为与被控对象数学模型结构相同的参考模型

(14)

其中：Nm(s)=1；Mm(s)为首一多项式。

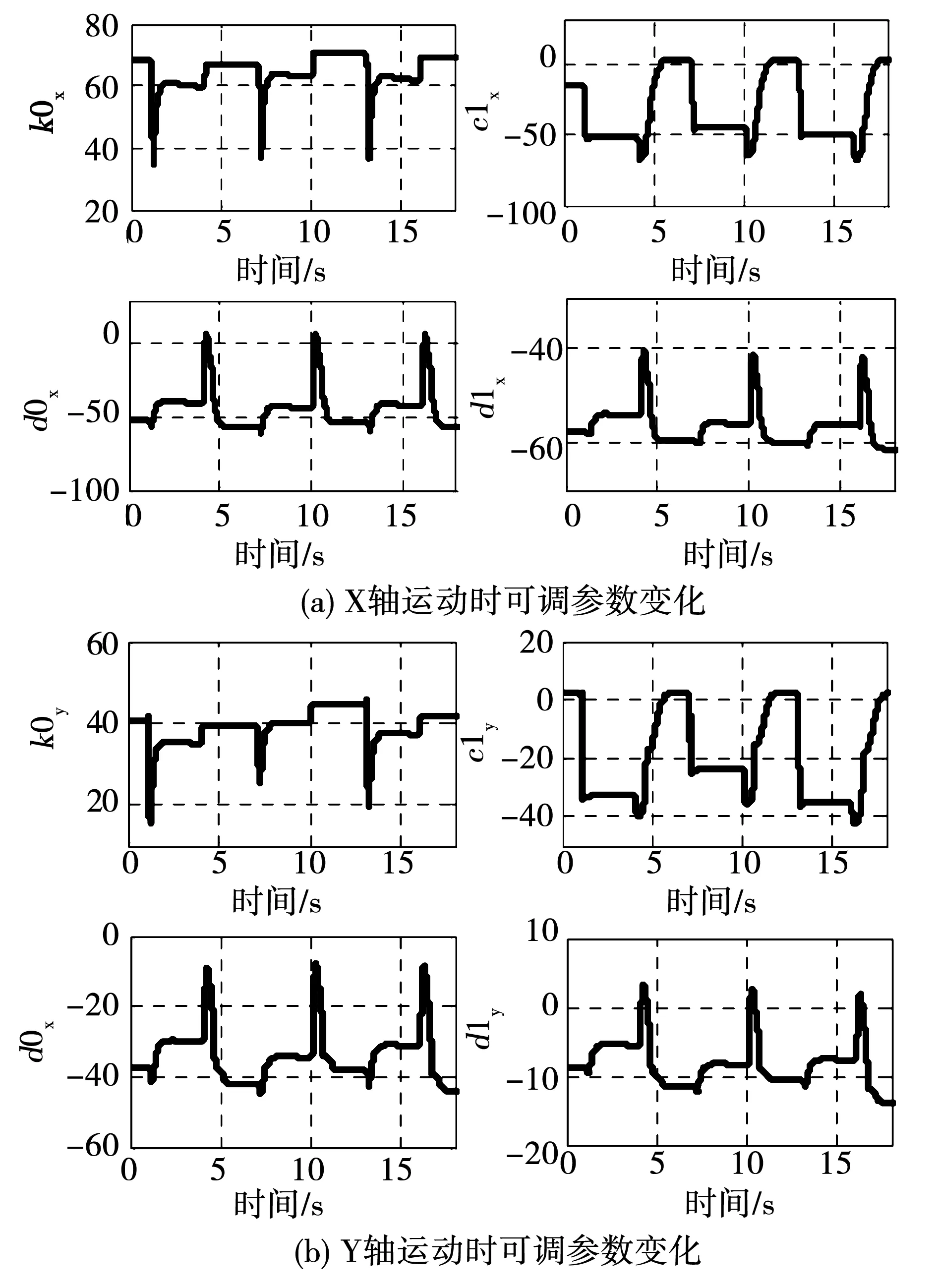
图6　平面开关磁阻电机的模型参考自适应控制系统Fig.6　　　　Model reference adaptive control system　　　 of the PSRM

由于参考模型的相对阶为2，为保证参考模型Wm严格正实，引入稳定多项式L(s)使L(s)Wm(s)严格正实，取L(s)为

L(s)=s+a, 0

(15)

式中a为常数且0

F1、F2为辅助信号发生器，其状态空间表达式和传递函数分别为：

(16)

(17)

式中：cT=[c1]、dT=[d1]和d0为可调参数向量； Λ=[-l1],l1>0；b=[1]；I为一阶单位矩阵。

根据图6所示的平面开关磁阻电机模型参考自适应控制系统可知，当可调系统传递函数与参考模型传递函数相匹配时

(18)

其中

(19)

模型匹配时

(20)

根据式(18)、式(20)可得

(21)

L-1(s)F(s)=Nm(s),

(22)

(23)

由式(22)得F(s)=Nm(s)L(s)，定义信号向量及滤波向量为：

(24)

根据Lyapunov稳定性理论，求得自适应律

(25)

其中：可调参数向量θ=[k0cTd0dT]，Γ为正定矩阵，通常为对角正定矩阵，em=yp-ym为系统实际输出与期望输出之间的误差。

可调参数向量θ可由式(26)得出

(26)

平面开关磁阻电机模型参考自适应控制系统的控制率为

(27)

3实验及结果分析

平面开关磁阻电机控制统结构框图和实验平台分别如图7和图8所示。实验平台由一台平面开关磁阻电机、六套电流驱动器、两套直线光栅尺系统、一套dSPACE标准组件系统、一台PC机和一台电源组成。其中，dSPACE标准组件系统包含具有1GHz主频的DS1005 PPC板处理器、具有24位位置计数器和5个通道的DS3001增量编码器接口板以及具有14位分辨率和32个通道的DS2103 D/A转换板。驱动器选用由美国AMC公司生产的可提供25A连续电流和50A峰值电流的50A20型直流伺服驱动器。电机位置传感器采用英国Renishaw公司Tonic系列的直线光栅尺系统，分辨率为100 nm。

图7　控制系统结构框图Fig.7　Structure diagram of the control system

图8　实验平台Fig.8　Experimental platform

通过最小二乘法分别辨识平面开关磁阻电机X轴和Y轴的力-位置模型参数，用于计算模型参考自适应控制器的可调参数初值，从而使系统快速进入稳定状态。平面开关磁阻电机X轴和Y轴运动时的系统模型参数辨识结果如图9所示。

图9　平面开关磁阻电机系统的模型参数Fig.9　Model parameters of the PSRM

基于dSPACE搭建的实验平台，分别对平面开关磁阻电机模型参考自适应位置控制系统在无负载以及在动子平台上增加2kg质量负载情况下进行了实验研究，电机X、Y轴的参考模型参数均选取am1=21，km=100，am2=100，X、Y轴两个方向的位置给定均为幅值15 mm、周期3 s的方波信号，实现平面开关磁阻电机在平面上(0，0)、(15，15)两点间进行往返的位置控制。平面开关磁阻电机X轴和Y轴的位置跟踪响应实验结果如图10所示，根据图10可知在无负载和带负载的情况下，电机的X轴和Y轴运动平台均能准确地跟踪给定位置，其中，X轴位置控制的调节时间为1.74 s， Y轴位置控制的调节时间为1.89 s；此外，位置跟踪局部放大图反映了动子平台在增加质量负载后，X、Y轴运动平台的阻尼增大，使电机跟踪出现滞后。平面开关磁阻电机X轴和Y轴位置跟踪误差如图11所示，位置跟踪误差局部放大图表明，在不增加质量负载时，X轴位置控制的稳态误差为±200 nm，Y轴位置控制的稳态误差为±500 nm；在动子平台增加质量负载后，X轴位置控制的稳态误差小于为±4.7 μm，Y轴位置控制的稳态误差为±4.3 μm。空载情况下，平面开关磁阻电机运行时的实时电流如图12所示，平面开关磁阻电机运动时X轴和Y轴模型参考自适应控制器的可调参数如图13所示，该图反映了电机在进行位置控制时控制器可调参数的动态调节过程。

图10　平面开关磁阻电机位置响应Fig.10　Position response of the PSRM

图11　平面开关磁阻电机位置误差Fig.11　Position error of the PSRM

图12　平面开关磁阻电机的实时电流波形Fig.12　Detected current of the PSRM

图13　　　　平面开关磁阻电机模型参考自适应控制器　　　的可调参数Fig.13　　　　Adjustable parameters of the model reference　　　 adaptive regulator of the PSRM

4结论

平面开关磁阻电机的6个动子绕组在动子平台上相互垂直交替排列，使其实现两轴的运动解耦。模型参考自适应控制方法在模型不确定的情况下，通过自适应律的作用，在线调整控制器参数，使电机输出稳定准确地跟随参考模型输出，从而实现平面开关磁阻电机的高精确度位置控制。研究表明：提出的平面开关磁阻电机模型参考自适应控制方法提高了电机的位置精确度，无负载时电机的稳态误差为±500 nm，增加质量负载后的电机稳态误差为±4.7μm，验证了提出的控制方法的可行性和有效性。

参 考 文 献:

[1]寇宝泉，张鲁，邢丰，等．高性能永磁同步平面电机及其关键技术发展综述[J]．中国电机工程学报，2013，33(9)：79-87.

KOU Baoquan,ZHANG Lu,XING Feng,et al.Development of the high-performance synchronous permanent magnet planar motor and its key technologies[J]. Proceedings of the CSEE,2013,33(9): 79-87.

[2]王太勇,乔志峰,韩志国,等. 高档数控装备的发展趋势[J].中国机械工程,2011,22(10) : 1247-1259.

WANG Taiyong,QIAO Zhifeng,HAN Zhiguo,et al. Development trends of high-end NC equipment[J]. China Mechanical Engineering,2011,22(10):1247-1259.

[3]PAN Jianfei,CHEUNG N C,YANG Jinming. High-precision position control of a novel planar switched reluctance motor[J]. IEEE Transactions on Industrial Electronics,2005,52(6):1644-1652.

[4]ZHANG Lu,KOU Baoquan,LI Liyi,et al. Modeling and design of an integrated winding synchronous permanent magnet planar motor[J]. IEEE Transactions on Plasma Science,2013,41(5):1214-1219.

[5]张新华,孙玉坤,项倩雯,等. 一种动圈式磁悬浮永磁平面电机实时电流分配策略[J].中国电机工程学报,2013,33(6): 144-152.

ZHANG Xinhua,SUN Yukun,XIANG Qianwen,et al. Analysis of real-time current distribution for magnetically levitated permanent-magnet planar motors with moving-coils [J]. Proceedings of the CSEE,2013,33(6): 144-152.

[6]曹家勇,朱煜,王劲松,等.平面电动机设计、控制与应用技术综述[J].电工技术学报,2005,20(4): 1-8.

CAO Jiayong,ZHU Yu,WANG Jinsong,et al. Survey of the state of the art in planar motor technology [J]. Transactions of China Electrotechnical Society,2005,20(4): 1-8.

[7]杨金明，张宙，潘剑飞，等．开关磁阻式平面电动机及其控制[J]．中国电机工程学报，2005,25(19) ：116-121.

YANG Jinming,ZHANG Zhou,PAN Jianfei. The control of the switched reluctance planar machine[J]. Proceedings of the CSEE,2005,25(19):116-121.

[8]PANJianfei,CHEUNG N C,GAN Waichuen,et al. A novel planar switched reluctance motor for industrial applications[J]. IEEE Transactions on Magnetics,2006,42 (10): 2836-2839.

[9]潘剑飞,曹广忠,张宙. 平面电机设计与控制[M].北京:科学出版社,2011.

[10]ZHAO Shiwei,CHEUNG N C,GAN Waichuen,et al. High-precision position control of a linear-switched reluctance motor using a self-tuning regulator[J]. IEEE Transactions on Power Electronics,2010,25(11): 2820-2827.

[11]PAN Jianfei,CHEUNG N C,YANG Jinming. Auto-disturbance rejection controller for novel planar switched reluctance motor[J]. IEE Proceedings-Electric Power Applications,2006,153(2): 307-316.

[12]杨金明,汪小平,赵世伟,等.开关磁阻平面电机的鲁棒控制[J].中国电机工程学报,2008,28(30): 104-108.

YANG Jinming,WANG Xiaoping,ZHAO Shiwei,et al. Robust control of planar switched reluctance motors [J]. Proceedings of the CSEE,2008,28(30): 104-108.

[13]PAN Jianfei,CHEUNG N C. An adaptive controller for the novel planar switched reluctance motor[J]. IET Electric Power Applications,2011,5(9): 677-683.

[14]曹广忠,潘剑飞,黄苏丹,等. 磁悬浮系统控制算法及实现[M].北京:清华大学出版社,2013.

[15]FANG Jilin,HUANG Sudan,CAO Guangzhong,et al. Optimization design of planar switched reluctance motors based on electromagnetic force characteristics[C]//IEEE International Power Electronics Systems and Applications Conference,Hongkong,China,2013.

[16]CAO Guangzhong,FANG Jilin,HUANG Sudan,et al. Optimization design of the planar switched reluctance motor on electromagnetic force ripple minimization[J]. IEEE Transactions on Magnetics,2014,50(11).

[17]HUANG Sudan,CAO Guangzhong,QIAN Qingquan,et al. Inverse force function for phase current estimation of the planar switched reluctance motor using sparse least squares support vector machines[C]//IEEE International Magnetics Conference,Dresden,Germany,2014.

[18]LJUNG L.System identification-theory for the user[M]. Prentice-Hall,1999.

(编辑：贾志超)

Position control of the planar switched reluctance motor based on model reference adaptive regulator

CAO Guang-zhong1,HUANG Su-dan2,WANG Ji-huan1,DUAN Ji-an3,QIAN Qing-quan2

(1. Shenzhen Key Laboratory of Electromagnetic Control,Shenzhen University,Shenzhen 518060,China;2. College of Electrical Engineering,Southwest Jiaotong University,Chengdu 610031,China;3.State Key Laboratory of High Performance Complex Manufactory,Central South University,Changsha 410083,China)

Abstract:To improve the positioning accuracy of the planar switched reluctance motor (PSRM),a position control method of the PSRM based on model reference adaptive control (MRAC) theory was proposed. The parameters of the linear model were identified for the PSRM by using the recursive least square algorithm. Taking the force command as the control quantity,the MRAC position controller was designed with the input and output on the basis of the Lyapunov stability theory. A real-time experimental platform is established based on dSPACE,and the position control of the PSRM was carried out. Experimental results demonstrate that the position control system of the PSRM with the MRAC tracks the reference position smoothly and accurately; the positioning accuracy is improved; the feasibility and effectiveness of the proposed control method is verified.

Keywords:planar switched reluctance motor; positioning accuracy; model reference adaptive control; Lyapunov stability theory; position control

收稿日期:2015-01-14

基金项目：国家自然科学基金(51275312);深圳市科技创新委员会项目(JSGG20141015153303491)

作者简介：曹广忠(1968—),男,博士,教授,研究方向为平面开关磁阻电机、先进控制理论及其应用、磁悬浮技术、电力电子技术等;

通讯作者:曹广忠

DOI:10.15938/j.emc.2016.06.001

中图分类号:TM 352

文献标志码:A

文章编号:1007-449X(2016)06-0001-08

黄苏丹(1986—),女,博士研究生,研究方向为平面开关磁阻电机、先进控制理论及其应用等;

汪济欢(1988—),男,硕士研究生,研究方向为平面开关磁阻电机控制;

段吉安(1969—),男,博士,教授长江学者,研究方向为先进制造技术与装备、机械系统动力学分析与控制等;

钱清泉(1936—),男,中国工程院院士,研究方向为铁道电气化与自动化。