任意空间位置线圈的互感计算方法

谢岳，　潘伟玲

(中国计量大学 机电工程学院，浙江 杭州 310018)



任意空间位置线圈的互感计算方法

谢岳，潘伟玲

(中国计量大学 机电工程学院，浙江 杭州 310018)

摘要:磁耦合谐振式无线电能传输技术通过空间分离线圈之间的电磁耦合实现电能的无线传递，耦合线圈尺寸的不同和相对位置的变化会引起线圈间的互感变化，继而影响无线电能传输系统的特性。以常见的矩形截面空心线圈为分析对象，对任意空间位置线圈间互感的计算方法进行研究，通过纽曼公式和细分求和法推导了互感的理论计算公式，为静态和动态无线电能传输系统的设计提供支持。在耦合线圈具有不同轴向距离、径向偏距及旋转角度等空间位置情况下，公式编程计算和实验测量结果都具有一致性，证明了计算方法的正确性。

关键词:无线电能传输；线圈互感；任意空间相对位置；矩形截面；细分求和；计算方法

0引言

磁耦合谐振式无线电能传输系统利用空间分离线圈之间的电磁耦合实现电能的传递，与传统的接触式电能传输方式相比，这种非接触方式在空间位置应用上具有更为灵活方便的特点。线圈间互感的大小和变化直接影响无线电能传输系统的传输功率及传输效率等特性[1-4]，研究任意空间位置线圈间的互感随线圈相对位置变动而变化的规律，对发射端初级线圈及接收端次级线圈的设计以及动态和静态无线电能传输有效范围的确定等具有重要的意义。线圈间的互感可以采用手册查表方式或有限元法等纯数值算法来计算，但这些方法首先需要确定模型参数，因此难以分析空间位置变化时互感的变化规律，并且会耗费大量的人力及计算机资源[5]。目前国内外关于不同条件下空心线圈间互感的解析公式主要是在磁矢势基础上推导得到或者直接利用纽曼公式进行分析，文献[6-8]分析了同轴条件下单匝圆环线圈之间、薄盘形线圈之间、薄壁螺线管之间以及这3种线圈之间互感的计算公式，文献[9-11]讨论了平行非同轴线圈之间互感的计算公式,文献[12-13]给出了轴线相交情况下单匝圆环线圈、薄盘形线圈、薄壁螺线管之间互感的计算方法，文献[14]推导了任意空间位置情况下单匝圆环线圈互感的计算公式。然而，以上这些研究对于任意空间位置具有一定截面的线圈之间的互感计算方法缺乏讨论。文献[15]给出了一种任意空间位置线圈互感的计算方法，该方法采用等效圆环回路法进行近似处理，即用两个分离的同轴圆环线圈模拟单个矩形截面线圈，但这种方法在两个任意空间位置线圈距离较近时会产生较大误差，并且当两个线圈相对位置发生变化时，互感计算所采用的坐标系需要重新确定，所以不利于编程计算，也不利于直接表达互感与空间位置的变化规律。

本文采用矩形截面圆环空心线圈为分析对象，对任意空间位置线圈互感的计算方法进行研究。通过纽曼公式可以推出任意空间位置的单匝圆环间互感的计算公式[14]，在此基础上采用细分求和法得到了任意空间位置矩形截面线圈互感的计算公式，同时搭建了基于ARM Cortex-M3内核的STM32F103主控制器及半桥逆变电路的任意空间位置线圈互感实验系统，实验和公式编程计算结果的一致性证明了计算方法的正确性。

1线圈互感空间计算模型

图1所示为矩形截面圆环空心线圈互感的空间计算模型，该模型由初级线圈和次级线圈组成。初次级线圈的线圈匝数、外径、内径和轴向厚度分别为Nx、rxo、rxi和hx，其中x=p表示初级线圈，x=s表示次级线圈。初级线圈的几何中心及中心轴分别与坐标系Oxyz的原点O及z轴重合，次级线圈的几何中心及中心轴分别与坐标系O′x′y′z′的原点O′及z′轴重合，坐标系O′x′y′z′的原点O′及z′轴的单位向量在坐标系Oxyz中分别表示为(Xs,Ys,Zs)及z′=ax+by+cz。分析矩形截面圆环空心线圈模型具有一般代表性，当rxo-rxi相对hx可忽略时，可等效为薄壁螺线管[8]；当hx相对rxo-rxi可忽略时,可等效为薄盘形线圈[7-8]；当线圈的轴向和径向尺寸相对半径都可忽略时，可等效为圆环线圈[8]。

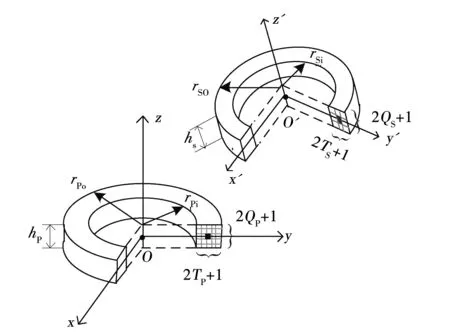
图1　矩形截面圆环空心线圈互感空间模型Fig.1　　　　Spatial mutual inductance model of rectangular　　　cross section air-core circular coils

2线圈互感计算公式

当电流通过具有一定截面的线圈时，电流是分布在整个截面上的。当电流频率较高时，会产生趋肤效应，这在很大程度上加大了互感计算的难度。因此为方便计算，有必要假定电流均匀地分布在线圈的截面上，并且采用细分求和法，即将电流细分为许多大小相等且集中流过面积可忽略的细分截面的电流元素的方法，该方法可以很好地减小或消除电流分布带来的互感计算误差影响[5]。

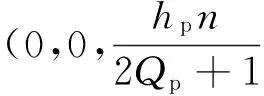
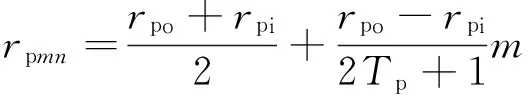
(1)

Pmn的等效线圈匝数为

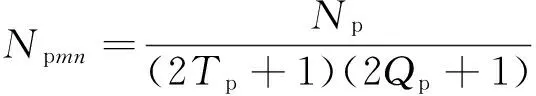
(2)

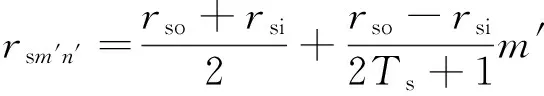
(3)

Sm′n′的等效线圈匝数为

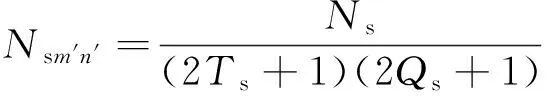
(4)

Mmnm′n′=

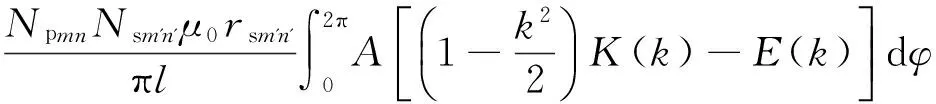
(5)

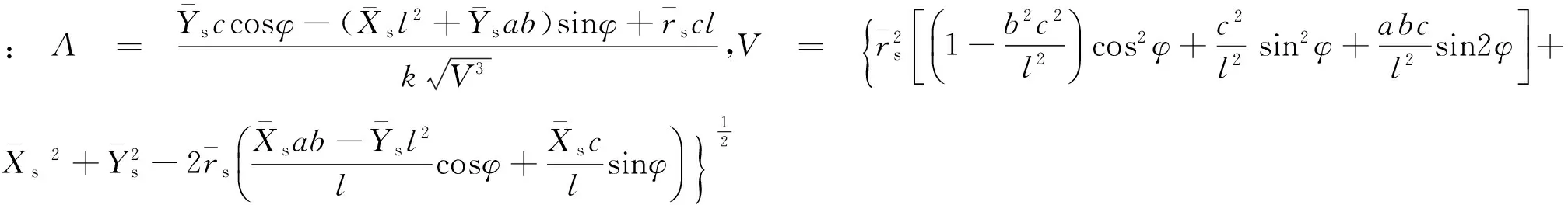
当l=0，即次级线圈中心轴单位向量z′与y轴平行时积分函数出现奇点，经处理后的互感计算公式为

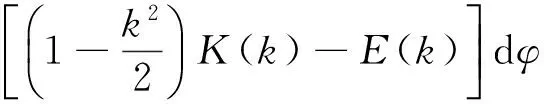
(6)

通过计算初级线圈元素与次级线圈元素间互感的总和便可求出两个线圈间的互感，即

Mps(Np,rpo,rpi,hp,Ns,rso,rsi,hs;

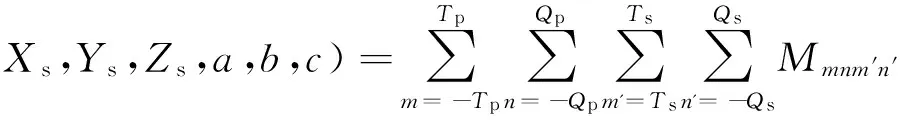
(7)

因此，线圈间的互感Mps取决于线圈的匝数和几何尺寸Np、rpo、rpi、hp、Ns、rso、rsi和hs，以及线圈间任意空间位置的6个自由度参数Xs、Ys、Zs、a、b和c。

3实验结果与分析

为了验证上述互感计算公式的正确性，搭建了如图2所示的任意空间位置线圈互感测量实验系统，该系统主要包括初级线圈Np、次级线圈Ns、基于ARM Cortex-M3内核的STM32F103主控制器、由MOSFET功率开关管IRF840(VT1和VT2)及稳压电容(C1和C2)构成的半桥逆变电路、IR2110驱动电路、谐振电容C、高精密采样电阻R0以及同步数据采集与信号处理系统组成。系统中初级线圈由半桥逆变电路供电，主控制器通过IR2110驱动电路控制半桥逆变电路输出电压方波，谐振电容与初级线圈自感L匹配，使得初级线圈电路谐振并得到正弦波电流。同步数据采集与信号处理系统通过测量初级线圈电流ip(t)和次级线圈开路电压us(t)计算线圈间的互感，此时该系统处在无线电能传输的空载状态。

搭建任意空间位置线圈互感测量实验平台如图3所示，其中初级及次级矩形截面圆环空心线圈均采用150×φ0.1利兹线绕制而成。初级及次级线圈的匝数和几何尺寸分别为Np=25匝、rpo=178 mm、rpi=159 mm、hp=10 mm、Ns=25匝、rso=141 mm、rsi=160 mm和hs=10mm。初级线圈自感L=206 μH，采样电阻R0=0.5±0.02% Ω，半桥逆变电路的输出电压频率为50kHz。实验中首先固定初级线圈，然后分别改变初级线圈与次级线圈同轴时的轴向距离Zs、Zs保持固定时改变径向偏移Xs以及Zs和Xs均固定时改变次级线圈平面相对初级线圈平面的旋转角度θ(a,b,c)，然后进行互感值的测量，同时利用Matlab软件对上述不同空间位置下的互感计算公式进行编程计算，并对实验及计算结果进行比较分析。编程计算时分别将初级和次级线圈的轴向和径向距离分为5等分。

图2　线圈互感测量实验系统原理图Fig.2　　　　Schematic diagram of coils′ mutual inductance　　　measurement experiment system

图3　任意空间位置线圈互感测量实验平台Fig.3　　　　Measurement experiment platform of mutual　　　inductance between arbitrarily positioned coils

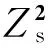
图4　线圈互感实验与计算结果图Fig.4　　　　Drawings of coils′ mutual inductance experimental　　　and calculating results

本实验中出现的误差主要包括理论计算误差和实验误差两个方面。Matlab软件采用双精确度数值计算，可减少计算过程中产生的误差；采用细分求和法时，细分份数不足将不能很好地代表电流在线圈截面上的实际分布，因此会产生理论计算误差，但是细分过度会导致计算量的增加，因此需要折衷。实验中初级线圈电流ip(t)和次级线圈开路电压us(t)的采样信号均采用屏蔽线传输，信号处理电路进行了校准。但是，线圈间任意空间位置的6个自由度参数Xs、Ys、Zs、a、b和c的实际测量误差会给公式计算带来较大的误差。考虑了这些误差因素后，从以上的实验、计算结果及误差分析来看，所给出的互感计算公式能很好地计算任意空间位置线圈的互感值。

4结论

本文首先建立了任意空间位置下矩形截面空心圆环线圈的互感计算模型，然后分别将初级和次级线圈等分为多个具有不同空间位置的线圈元素，在利用纽曼公式推导出的初次级线圈元素间互感的计算公式基础上，采用细分求和法得到具有矩形截面空心圆环线圈任意空间位置的互感计算公式，并且搭建了任意空间位置线圈互感测量实验平台，在多个不同线圈空间位置条件下对线圈互感值进行实验测量和编程计算，互感实验值和编程计算值的一致性表明了任意空间位置互感计算公式的正确性，这对于无线电能传输系统发射端初级线圈及接收端次级线圈等的设计具有重要的参考价值。

参 考 文 献:

[1]BHUYAN S,SIVANAND K,PANDA S K.Effect of design para- meters on resonant wireless energy transfer system[J]. Journal of Electromagnetic Waves and Applications,2013,27(3):288-298.

[2]翟渊,孙跃,戴欣,等. 磁共振模式无线电能传输系统建模与分析[J]. 中国电机工程学报,2012,32(12):155-160.

ZHAI Yuan,SUN Yue,DAI Xin,et al. Modeling and analysis of magnetic resonance wireless power transmission systems[J]. Proceedings of the CSEE,2012,32(12):155-160.

[3]罗斌,生茂常,吴仕闯,等. 磁谐振耦合式单中继线圈无线功率接力传输系统的建模与分析[J]. 中国电机工程学报,2013,33(21):170-177.

LUO Bin,SHENG Maotang,WU Shichuang,et al. Modeling and analysis of magnetic resonance coupling wirel ess relay power transfer system with single intermediate coil resonator[J]. Proceedings of the CSEE,2013,33(21): 170-177.

[4]JONAH O,GEORGAKOPOULOS S V.Wireless power transfer in concrete via strongly coupled magnetic resonance [J]. IEEE Transactions on Antennas and Propagation,2013,61(3):1378-1384.

[5]卡兰塔罗夫,采伊特林. 电感计算手册[M]. 北京: 机械工业出版社,1992. 294-339.

[6]BIELER T,PERROTTET M,NGUYEN V,et al. Contactless power and information transmission[J]. IEEE Transaction on Industry Applications,2002,38(5):1266-1272.

[7]BABIC S,SHEPPARD S,AKYEL C.The Mutual inductance of two thin coaxial disk coils in air[J]. IEEE Transaction on Magnetics,2004,40(2):822-825.

[8]BABIC S,AKYEL C.Improvement in calculation of the self and mutual inductance thin-wall solenoids and disk coils[J]. IEEE Transaction on Magnetics,2000,36(4):1970-1975.

[9]CONWAY J T.Inductancecalculations for noncoaxial coils using bessel functions[J]. IEEE Transaction on Magnetics,2007,43(3):1023-1034.

[10]KIM K,LEVI E,ZABAR Z.Mutual inductance of noncoaxial circular coils with constant current density[J]. IEEE Transaction on Magnetics,1997,33(5):4303-4309.

[11]CONWAY J T.Noncoaxial inductance calculations without the vector potential for axisymmetric coils and planar coils[J]. IEEE Transaction on Magnetics,2008,44(4):453-462.

[12]刘修泉,曾昭瑞,黄平. 空心线圈电感的计算与实验分析[J]. 工程设计学报. 2008,15(2):149-153.

LIU Xiuquan,ZENG Zhaorui,HUANG Ping. Numerical and experimental analysis on performances of coreless coil inductance[J]. Journal of Engineering Design. 2008,15(2):149-153.

[13]BABIC S I,AKYEL C.Calculating mutual inductance between circular coils with inclined axes in air[J]. IEEE Transaction on magnetics，2008,44(7):1743-1750.

[14]BABIC S,SIROIS F,AKYEL C,et al. Mutual inductance calculation between circular filaments arbitrarily positioned in space: alternative to Grover’s formula[J]. IEEE Transaction on Magnetics,2010,46(9):3591-3600.

[15]罗垚,陈柏超,袁佳歆,等. 倾斜轴空心矩形截面圆柱线圈互感计算[J]. 电工技术学报. 2012,27(5) : 132-136.

LUO Yao,CHENBaichao,YUAN Jiaxin,et al. Mutual inductance calculations of inclined axial air-core circular coils with rectangular cross sections. Transactions of China Electrotechnical Society. 2012,27(5):132-136.

(编辑：贾志超)

Mutual inductance calculation method of arbitrary space positioned coils

XIE Yue，PAN Wei-ling

(Department of Electrical and Mechanical Engineering,China Jiliang University,Hangzhou 310018,China)

Abstract:The magnetic coupling resonant wireless power transfer technology realizes the power transfer wirelessly by means of electromagnetic coupling between space-separated coils. The different sizes and relative position change of coupling coils may cause the mutual inductance magnitude variation,which can thereby influence the performance of wireless power transfer system. Taking the common rectangular cross section air-core coils as the analysis object,the calculation method of mutual inductance between arbitrary space positioned coils was researched and the relevant theoretical formula was derived based on Neumann equation and method of subdivision and superposition. The calculation formula can give the support to the design of both static and dynamic wireless power transfer systems. The correctness of the proposed calculation method was proved by the consistency of the experimental results and the formula programming calculation results under the condition of different space positions such as different axial distances,radial distances and rotation angles between the coupling coils.

Keywords:wireless power transfer; mutual inductance of coils; arbitrary relative space position; rectangular cross section; method of subdivision and superposition; calculation method

收稿日期:2015-03-25

基金项目：国家自然科学基金(51275499)

作者简介：谢岳(1964—)，男，博士，教授，研究方向为电力电子技术、检测技术与自动化装置; 潘伟玲(1991—)，女，硕士，研究方向为检测技术与自动化装置。

通讯作者:谢岳

DOI:10.15938/j.emc.2016.06.008

中图分类号:TM 153,TM 551

文献标志码:A

文章编号:1007-449X(2016)06-0063-05