三相APF考虑饱和限幅稳定性控制方法

张梦华,　程新功，　宗西举，　王洪杰，　王玉真

(1.济南大学 自动化与电气工程学院，山东 济南 250022；2.广州地铁设计研究院有限公司，广东 广州 300072)



三相APF考虑饱和限幅稳定性控制方法

张梦华1,程新功1，宗西举1，王洪杰2，王玉真1

(1.济南大学 自动化与电气工程学院，山东 济南 250022；2.广州地铁设计研究院有限公司，广东 广州 300072)

摘要:针对APF(active power filter)在控制中的混杂特性和饱和非线性问题，提出一种将切换算法和空间电压矢量控制算法相结合并应用于考虑饱和限幅的三相APF的控制策略。该方法首先建立三相APF的切换仿射线性系统的误差模型，根据Lyapunov相关定理及凸集理论，为考虑饱和限幅的三相APF找到了一种新的、保守型更小的切换率。然后根据三相电源电压构成的空间电压矢量图及波形图，三相电源电压被分成六个扇区，再根据凸组合稳定条件，在每个扇区内找到可以保证系统二次稳定的开关子系统的组合，在这些子系统的组合中选取使得Lyapunov函数导数最小的子系统。最后仿真分析和实验结果证明了所提出方法的可行性和正确性。

关键词:有源电力滤波器；空间电压矢量控制；李亚普诺夫函数;饱和限幅；切换仿射线性系统

0引言

近年来电力电子技术发展迅速，它给人们带来利益和方便，同时给电网带来的谐波污染问题也日益严峻[1]。有源电力滤波器能够动态的治理各次谐波，因而成为了谐波滤除的发展方向[2]。目前主要研究的是有源电力滤波器(active power filter,APF)的建模、控制方法、补偿性能、谐波抑制方法及谐波检测方法[3-6]，很少提及APF稳定性分析。

文献[7]利用Lyapunov函数分析了其所提控制算法的稳定性，并且根据闭环传递函数分析了APF部分稳定性。文献[8]提出一种同时检测负载电流和电源电压来控制APF输出电流的控制方案，所提控制方案可以使系统变稳定，并且具有理想的补偿效果。文献[9-11]将切换系统相关理论应用于三相APF控制方法的研究上，根据Lyapunov相关定理，为系统找到了能够保证其二次稳定的切换率。但是以上各个算法都没有考虑饱和非线性对系统影响。在实际工程中，各个参数都有额定值的限制，因此均会受到饱和非线性的影响。若超过系统的额定值，传统的处理方法是将设备切除或者设置设备以额定值运行。但是将设备切除成本较大，不经济。若设置设备以额定值运行可能会使原本稳定的系统变得不稳定，并且产生新的平衡点以及极限环等[12]。

基于实际工程中出现的问题，本文提出了一种新的考虑饱和限幅的三相有源电力滤波器的控制方法。根据Lyapunov相关定理、凸集理论、凸组合条件将切换控制和空间电压矢量控制方法相结合，为考虑饱和限幅的三相APF找到了一种新的、简单的稳定性判据。该算法由于合理的应用零矢量，因此明显的降低了逆变器的开关损耗。

1三相APF的切换仿射线性系统的误差模型

图1给出了三相APF的拓扑结构。图中Uk(k=a,b,c)是三相电源电压,isk是电源电流,iLk是非线性负载电流,ick是APF产生的补偿电流，UDC是APF的直流侧电压。S1～S6分别代表APF的6个IGBT。用Sk表示开关状态，取值如下：

其中三相APF一共有八种开关模态，如表1所示。

图1　三相APF的拓扑结构Fig.1　Topological structure of three phase APF

开关模态SaSbScⅠ000Ⅱ001Ⅲ010Ⅳ011Ⅴ100Ⅵ101Ⅶ110Ⅷ111

对于图1，根据基尔霍夫电压定理得

(1)

其中：uaN，ubN，ucN分别为点a,b,c与电源中性点N之间的电压降。

由于三相APF直流侧输出电压UDC的变化率远远小于APF产生的补偿电流的变化率，因此在一个采样周期中可认为UDC不变，那么系统状态方程可写为

Ax+Bi，i=1，2，…，8。

(2)

AΔx+bii=1，2，…，8。

(3)

2考虑饱和限幅的三相APF的二次稳定切换控制

连续时间状态饱和系统的一般形式为：

(4)

其中：

A=[aij]∈Rn×n

x=[x1x2… xn]T,-Imax≤xi≤Imax,

i=1,2,…,n

并且有

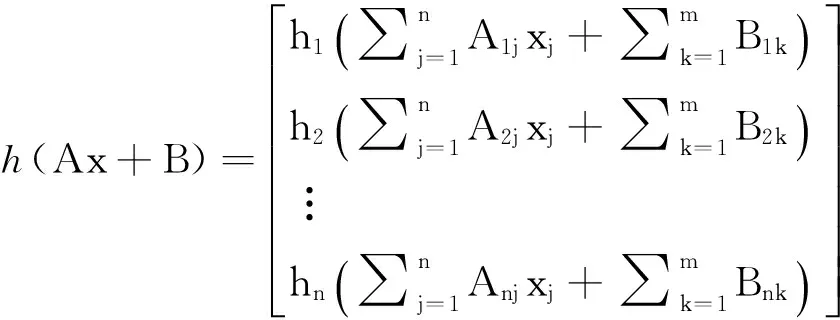
(5)

令

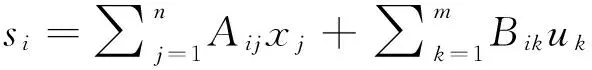
(6)

其中hi(·)定义为

(7)

式(5)和式(7)共同保证了系统所有的状态都被限制在-Imax和Imax之间。

对饱和系统有引理1成立。

引理1[12]:如果G=[gij]∈Rn×n为(行)对角占优阵，并且其对角元素均为负(即对于所有的i=1,2,…,n，都有gii<0), 那么对于任意独立于x的矩阵B=[B1B2… Bn]T∈Rn，都有

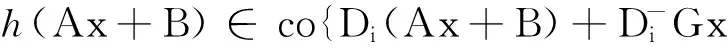
Di∈Dn,i=1,2,…,2n}。

(8)

对于考虑饱和限幅的三相APF的二次稳定性，有如下结论:

定理1：对于2≤m≤8，如果存在一个凸组合λ=[λ1… λm]T以及一个主对角元素为负的行对角占优矩阵G使得

(9)

那么在切换规则:

(10)

的作用下，Δxd=0是一个可以保证系统二次稳定的切换平衡点。

证明：选择Lyapunov函数为

由引理1得

ΔxTh(Ax+Bj)≤

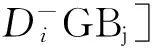
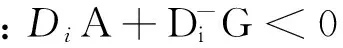
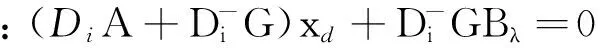
则有

由Lyapunov定理知：系统的平衡状态是渐近稳定的。

推论1：对于2≤m≤8，如果存在一个凸组合λ=[λ1… λm]T以及一个主对角元素为负的行对角占优矩阵G使得

(11)

那么在切换规则：

(12)

的作用下，Δxd=0是一个可以保证系统二次稳定的切换平衡点。

证明：定理1的切换规则为

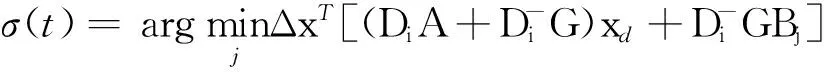
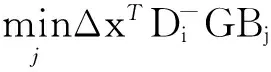
推论1和定理1是等价的，但是大大简化了算法。

3切换和空间电压矢量控制结合法

由(2)式可得

(13)

由于滤波电感L和电阻R上的电压远远小于电源相电压，可以把它忽略掉，因此有：

(14)

等式右面即为SVPWM的参考输入，因此可证明三相电源电压Ua，Ub，Uc即为SVPWM的参考输入。图2给出了系统三相电源电压波形图，按每60°为一个间隔，共将之分为6个区间。

在0～120°区间，相电压Uc最小，因此系统在此区间运行时始终有Sc=0。同理：在120°～240°区间，相电压Ua最小，因此系统在此区间运行时始终有Sa=0。在240°～360°区间，相电压Ub最小，因此系统在此区间运行时始终有Sb=0。

图2　三相正弦电压波形Fig.2　Three-phase grid voltage waveforms field

三相电源电压Ua，Ub，Uc构成的空间矢量分布图如图3所示。

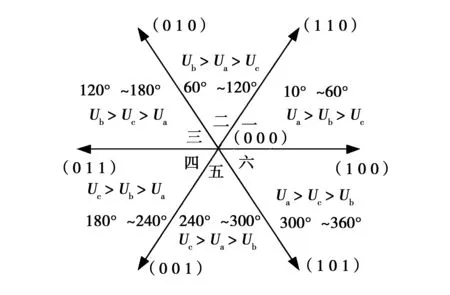
图3　空间矢量分布图Fig.3　Diagram of voltage space vectors

在0～60°区间，即扇区一，Sc=0，这样就只需另外两个桥臂的开关动作。根据Sa，Sb，Sc的变化可以把系统看成为4个线性子系统组成的线性切换系统Ⅰ、Ⅲ、Ⅴ、Ⅶ，其中各子系统的开关函数取值如表1所示。为减少开关损耗，确定2组开关序列：Ⅰ、Ⅲ、Ⅶ和Ⅰ、Ⅴ、Ⅶ。经计算开关序列Ⅰ、Ⅲ、Ⅶ不符合条件。以开关序列Ⅰ、Ⅴ、Ⅶ为例。

当Sa=0,Sb=0,Sc=0时：

当Sa=1,Sb=0,Sc=0时：

当Sa=1,Sb=1,Sc=0时：

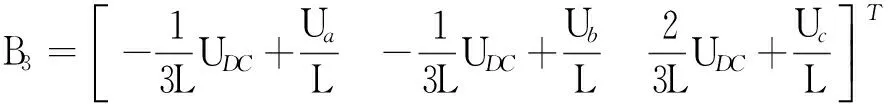
分析B1、B2、B3可知：总有λ1+λ2+λ3=1, (λi∈(0,1),i=1,2,3)，使得

即为

(15)

整理得

(16)

满足式(9)、式(11)，即满足定理1和推论1的条件。

同理对其他扇区进行分析，对于每一个扇区，都可以找到三个切换子系统满足定理1和推论1的条件。如表2所示。

表2三相APF 在各扇区开关序列及开关函数

Table 2Switching modes and switching functions of

three-phase APF in each sector

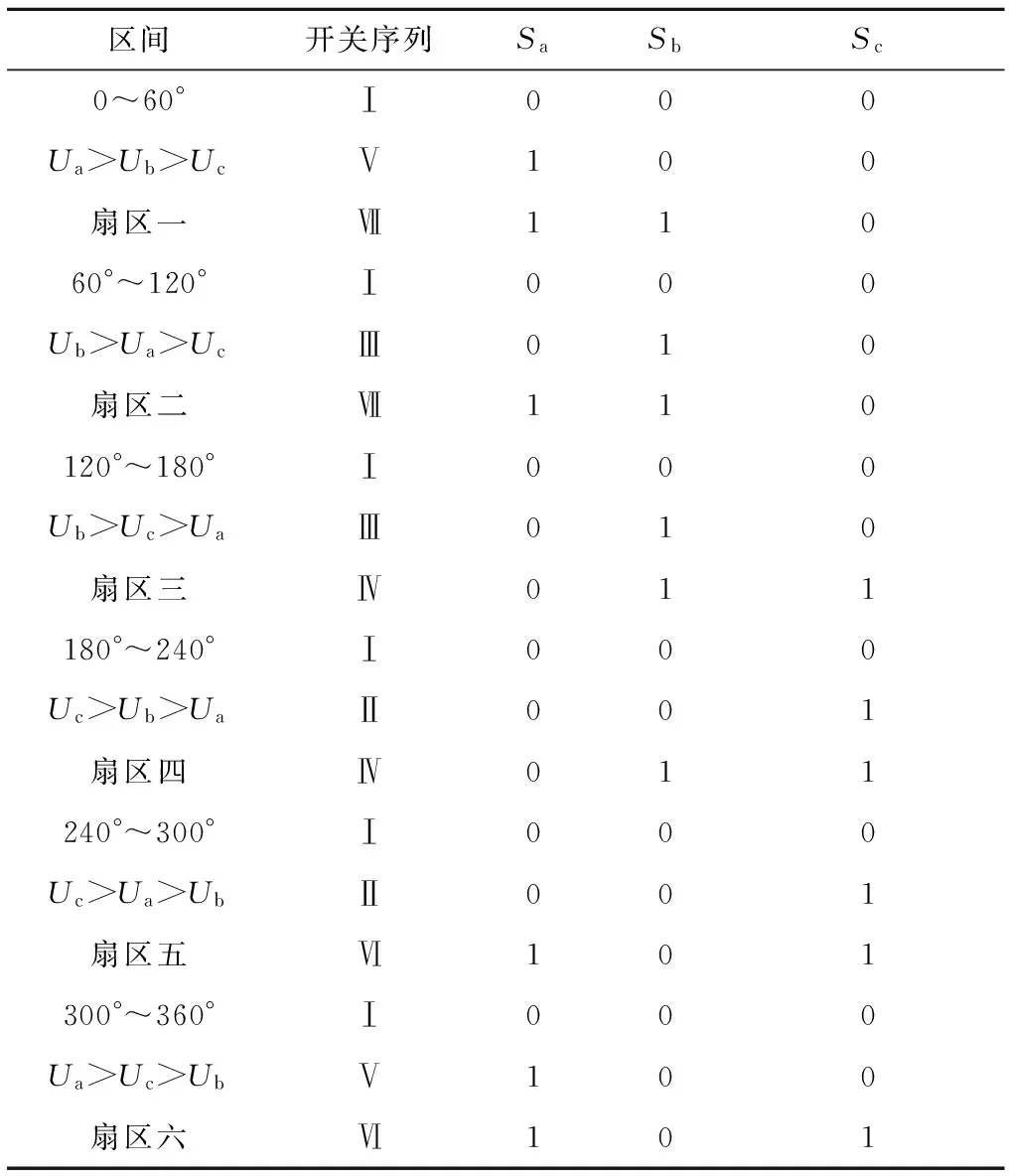
区间开关序列SaSbSc0～60°Ⅰ000Ua>Ub>UcⅤ100扇区一Ⅶ11060°～120°Ⅰ000Ub>Ua>UcⅢ010扇区二Ⅶ110120°～180°Ⅰ000Ub>Uc>UaⅢ010扇区三Ⅳ011180°～240°Ⅰ000Uc>Ub>UaⅡ001扇区四Ⅳ011240°～300°Ⅰ000Uc>Ua>UbⅡ001扇区五Ⅵ101300°～360°Ⅰ000Ua>Uc>UbⅤ100扇区六Ⅵ101

4仿真结果与分析

图4　APF控制系统框图Fig.4　Block diagram of APF control system

初始APF对整流桥进行谐波补偿，在0.5 s时负载发生突变。APF的控制策略分别采用不考虑饱和非线性[13]及考虑饱和非线性的两种切换方式。假设前者运行方式为1，后者运行方式为2。通过仿真，比较两种控制策略的补偿效果。

负载突变后电网谐波电流增大，由于APF的自身容量的限制，需要根据额定容量对参考谐波电流进行抑制。图5中iL1,iL2,iL分别为不控整流桥1、不控整流桥2、总的负载电流的波形图。

图5　iL1,iL2及iL波形Fig.5　Waveforms of iL1,iL2,and iL

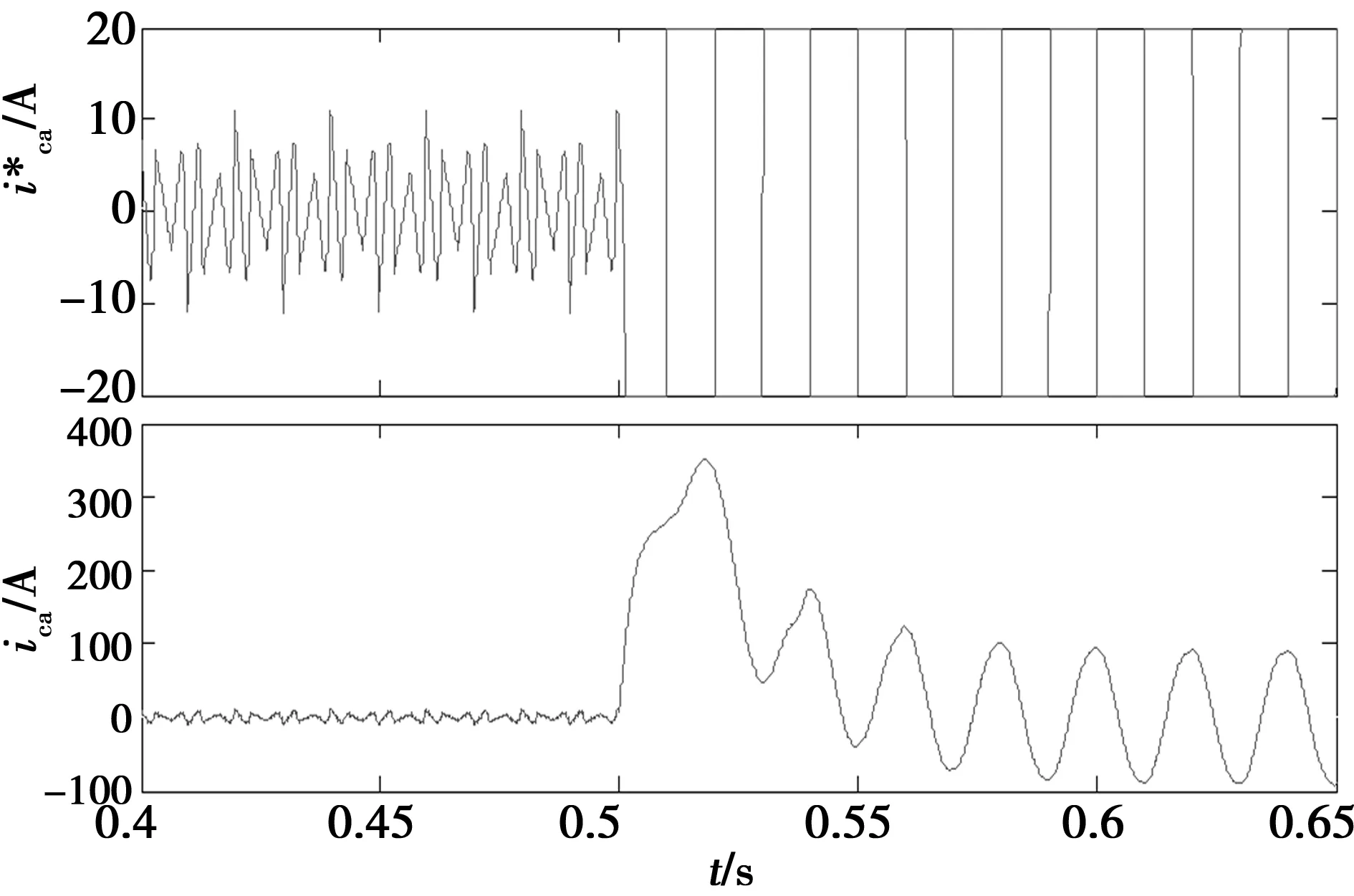
图6　　　　方式1作用下谐波参考电流　　　及APF实际输出电流icaFig.6　　　　Compensation currentand icaunder mode 1

图7　　　　方式1作用下电网电流isa，直流侧电压UDC波形Fig.7　　　　Waveform of the system current isaand　　　dc bus voltage UDCunder mode 1

图8　　　　方式2作用下电网电流isa、直流侧电压UDC的波形Fig.8　　　　Waveforms of the system current isaand　　　dc bus voltage UDCunder mode 2

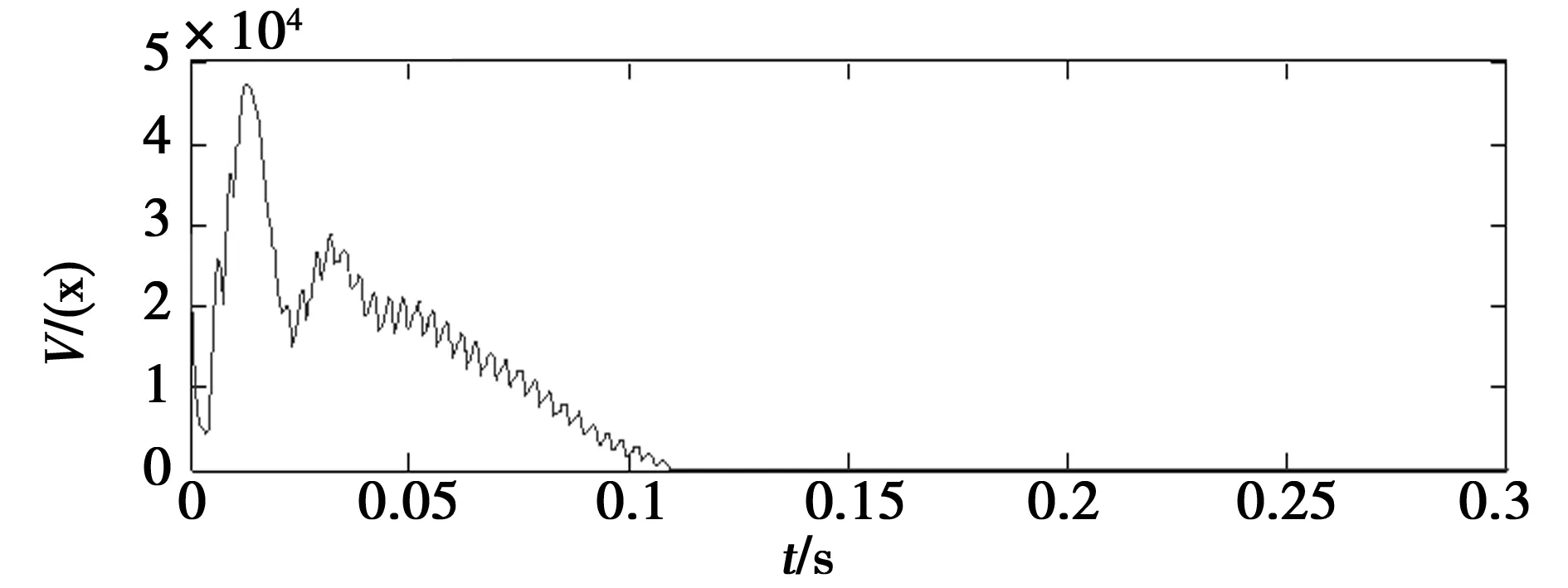
图9　李亚普诺夫函数V(x)Fig.9　Lyapunov function V(x)

图10　饱和前电源电流isa频谱图Fig.10　　　　Spectrum diagram of supply current isa　　　before saturation

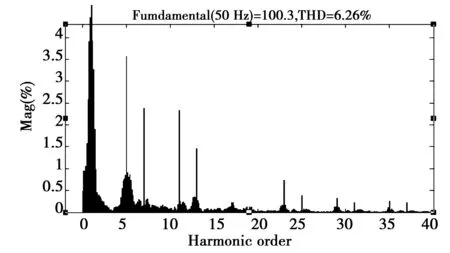
图11　饱和后电源电流isa频谱图Fig.11　　　　Spectrum diagram of supply current isa　　　after saturation

图12所示为三相开关的驱动信号，当C相电压最小时，Sc=0，即只需另外两个桥臂的开关进行切换。而未考虑饱和限幅的切换控制则需要三个桥臂的开关同时进行切换，所以在同一个控制时刻，提出的控制策略所需要切换的开关个数减少1/3，因此相对应的开关损耗相比未考虑饱和限幅的切换控制大大降低。

图12　Sa，Sb，Sc各开关驱动信号Fig.12　Driver signals for switches Sa，Sb，Sc

5实验结果

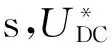
图13　APF主电路Fig.13　Main circuit of APF

图14　APF控制器Fig.14　Controller of APF

图15给出了饱和前后直流侧电压UDC、A相负载电流iLa、电源电流isa的波形图。图16给出了A相补偿电流的波形图，从图中可以看出，APF产生的补偿电流都被限制在的10 A以内。

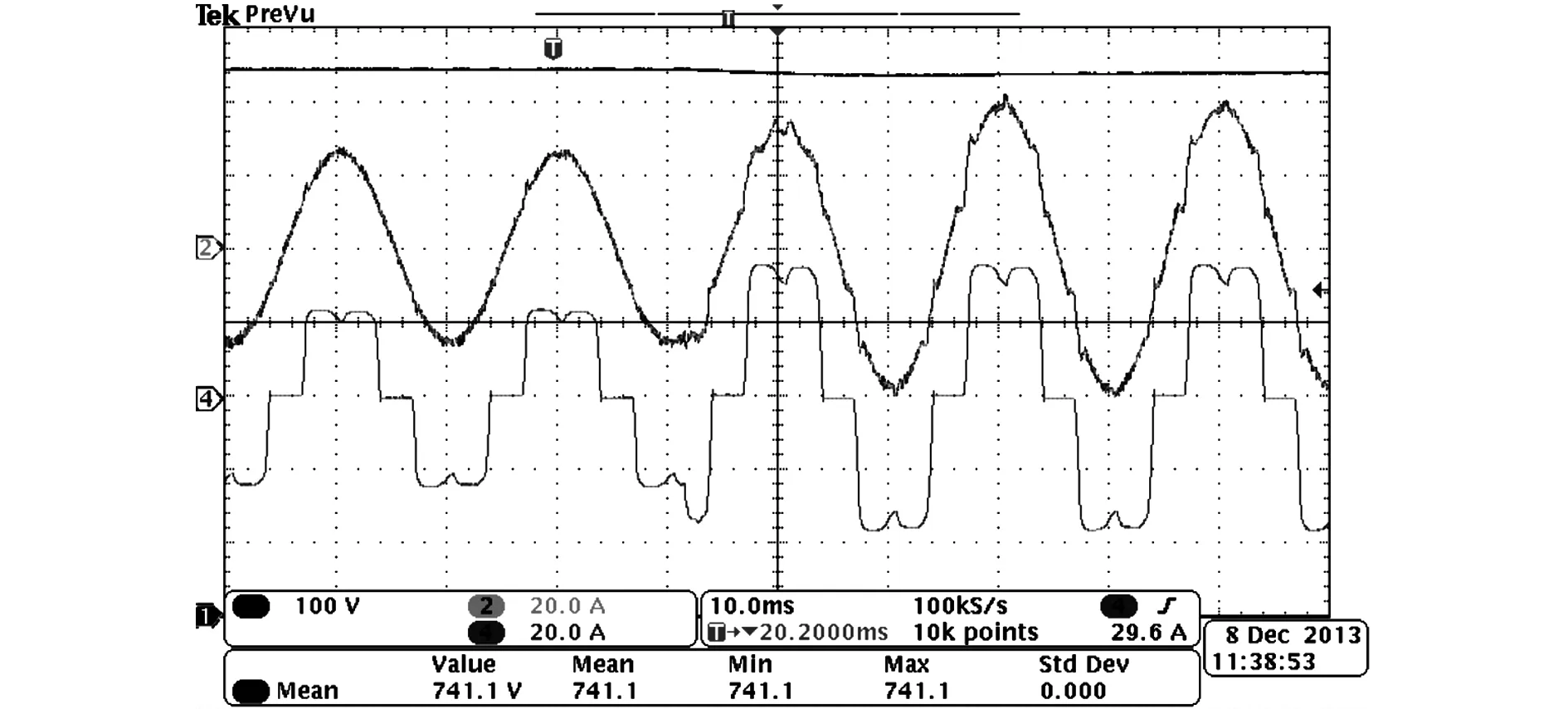
图15　　　　饱和前后直流侧电压UDC、A相负　　　载电流iLa、电源电流isa的波形图Fig.15　　　　Waveforms of UDC,iLaand isa　　　 before and after saturation

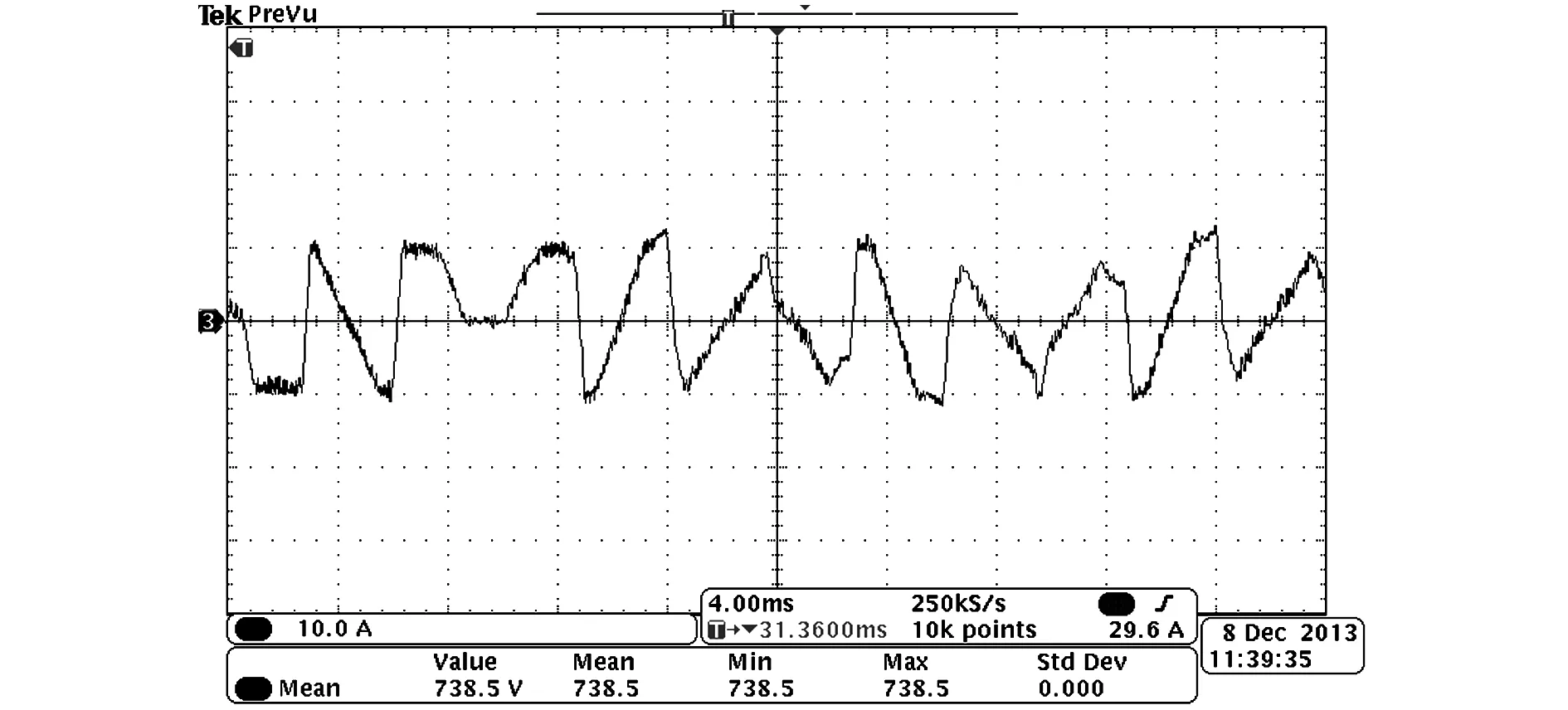
图16　考虑饱和限幅的APF产生的补偿电流Fig.16　Compensation current under constraints

图17所示为饱和前三相电源电流谐波分析图。由于受AD转换速度和DSP的处理速度的限制，实验样机中采样周期要比仿真中的采样周期大的多，因此补偿后的电源电流谐波含量并没有像仿真结果中的那样低，三相电源电流谐波畸变率为2.0%左右。图18所示为饱和后三相电源电流谐波分析图。由图可知，在发生饱和限幅时，考虑饱和限幅的切换控制算法仍有很高的跟踪精确度。

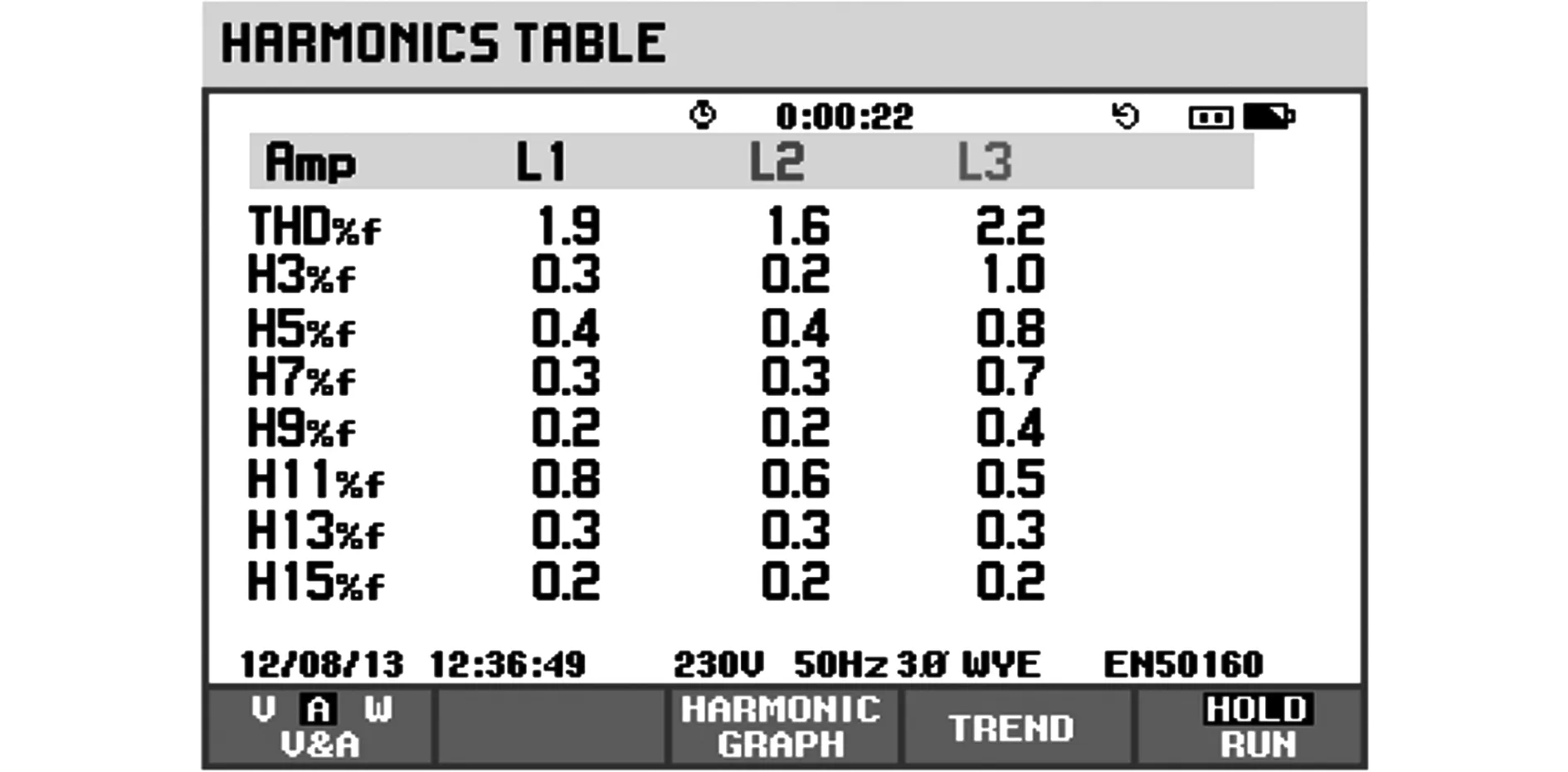
图17　饱和前A、B、C三相电源电流谐波分析Fig.17　　　　Harmonic analysis of three-phase supply　　　current before saturation

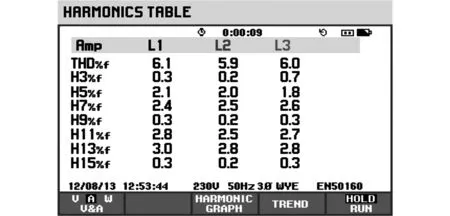
图18　饱和后A、B、C三相电源电流谐波分析Fig.18　　　　Harmonic analysis of three-phase supply　　　current after Saturation

经计算未考虑饱和限幅的切换控制作用下的开关损耗为360 W,而考虑饱和限幅的切换控制作用下的开关损耗为280W, 由此可知采用本文提出的控制算法可以大大的减小开关损耗。

6结论

本文建立了三相三线制APF的切换仿射线性系统的误差模型，基于Lyapunov稳定性定理和凸集理论，为考虑饱和限幅的三相APF找到了一种新的、保守型更小的稳定性判据。然后将得到的切换控制算法和空间电压矢量控制算法相结合，根据三相电源电压构成的空间电压矢量图及波形图，三相电源电压被分成六个扇区，再根据凸组合稳定的条件，找到了一个非常简单的切换律，大大简化了算法。该算法由于合理的运用零矢量，因此明显的降低了逆变器的开关损耗。

参 考 文 献:

[1]张晓，孔令军．三相三线制并联型有源电力滤波器的准滑模变结构控制[J]．电力系统保护与控制，2011, 39(21)：40-44．

ZHANG Xiao, KONG Linjun. The quasi-sliding mode control of the shunt active power filter in three-phase three-wire system [J]. Power System Protection and Control, 2011, 39(21): 40-44.

[2]汤赐，罗安，赵伟等．混合型并联有源电力滤波器的稳定性[J]．中国电机工程学报，2008, 28(6):43-48．

TANG Ci, LUO An, ZHAO Wei, et al. Stability of Hybrid Shunt Active Power Filter [J]. Proceeding of the CSEE, 2008, 28(6): 43-48.

[3]陈菊明，刘峰．基于无源化方法的三相四线制APF控制器策略[J]．电力系统自动化，2006, 30(8):32-36．

CHEN Juming, LIU Feng. Passivity-based controller for three phase four-wire APF[J]．Automation of Electric Power Systems, 2006, 30(8):32-36.

[4]李玉梅，马伟明．无差拍控制在串联电力有源电力滤波器中的应用[J]．电力系统自动化，2001, 25(4):28-30．

LI Yumei, MA Weiming. Application of deadbeat control in series active power filter [J]. Automation of Electric Power Systems, 2001, 25(4):28-30.

[5]楚烺，涂春鸣，罗安，等．不同类型谐波源综合补偿的串联混合型APF设计[J]．电力系统自动化，2013, 37(8):123-128．

CHU Lang, TU Chunming, LUO An, et al. A series hybrid APF design for integrated compensation of different types of harmonic sources [J]. Automation of Electric Power Systems, 2013, 37(8):123-128.

[6]王群，姚为正，刘进军，等．谐波源与有源电力滤波器的补偿特性[J]．中国电机工程学报，2001, 21(2):16-20．

WANG Qun, YAO Weizheng, LIU Jinjun, et al. Hamonic source and compensation characteristics of active power filters[J]. Proceedings of the CSEE, 2001, 21(2):16-20.

[7]于晶荣，滕召胜．有源电力滤波器预测电流控制及稳定性分析[J]．电工技术学报.2009, 24(7):164-170．

YU Jingrong, TENG Zhaosheng. Predictive current control and stability analysis of active power filter[J]. Transactions of China Electrotechnical Society, 2009, 24(7): 164-170.

[8]吴隆辉，卓放，张鹏博，等．并联混合型有源电力滤波器稳定性及控制方法[J]．中国电机工程学报，2008, 28(18): 54-60．

WU Longhui, ZHUO Fang, ZHANG Pengbo, et al. Stability analysis and controller design of hybrid parallel active power filter[J]. Proceedings of the CSEE, 2008, 28(18): 54-60.

[9]张永峰，程新功,宗西举，等．单相有源电力滤波器的非线性切换控制[J]．电力系统保护与控制，2011, 39(18):139- 144．

ZHANG Yongfeng, CHENG Xingong, ZONG Xiju, et al. Nonlinear switching control of si ngle-phase active power filter [J]. Power System Protection and Control, 2011, 39(18):139-144.

[10]李春文，汤洪海，郑雪生，等．三相APF的切换系统建模与二次最优控制[J]．中国电机工程学报，2008, 28(12): 66-72．

LI Chunwen, TANG Honghai, ZHENG Xuesheng, et al. Modeling and quadratic optimal control of three-phase APF based on switched system[J]. Proceedings of the CSEE, 2008, 28(12):66-72.

[11]郭晓云，刘会金，曹玉胜，等．基于切换仿射线性模型的三相APF电流控制方法[J]．中国电机工程学报，2011, 31(4):59-65．

GUO Xiaoyun, LIU Huijin, CAO Yusheng, et al. A novel current control method for three-phase APF based on switched affine model[J]. Proceedings of the CSEE, 2011, 31(4):59-65.

[12]刘太珲，状态饱和系统分析[D].硕士学位论文，浙江大学，控制理论与控制工程，浙江大学，2007．

[13]程新功，张梦华，宗西举，等．三相APF切换和空间电压矢量联合控制方法[J]．电机与控制学报，2014, 18(12): 57-63．

CHENG Xingong, ZHANG Menghua, ZONG Xiju, et al. Control methods of three-phase active power filter based on switch and space voltage vector[J]. Electric Machines and Control, 2014, 18(12): 57-63..

(编辑：刘素菊)

Stabilization of the three-phase active power filter under state saturation constraints

ZHANG Meng-hua1,CHENG Xin-gong1,ZONG Xi-ju1,WANG Hong-jie2,WANG Yu-zhen1

(1.School of Electrical and Engineering, University of Jinan,Jinan 250022, China;2.Guangzhou Metro Design & Research Institute Co., Ltd, Guangzhou 300072,China)

Abstract:Combining switching control with space voltage vector, a method which applies to three-phase APF considering saturation limiting was proposed. First, error model of switching system of three-phase APF was established. A novel conservative stability criterion was found for saturation limiting based on Lyapunov stability theorem and convex set theory. And then according to space vector figure and waveform, three phase supply voltage was divided into six sectors. Switch subsystem combination which meets quadratic stability requirement was chosen in each sector from convex stability requirement. The subsystem which made Lyapunov derivation the minimum was chosen in the subsystem combination which met quadratic stability requirement. Finally, the simulation analysis and experimental results proved the correctness and feasibility of the proposed method.

Keywords:active power filter; space voltage vector control; Lyapunov function; saturation constraints; switched affine linear system

收稿日期:2014-08-07

基金项目：国家自然科学基金(11201179); 山东省自主创新专项基金(2012CX30302)

作者简介：张梦华(1988—), 女，博士，研究方向为电力电子；

通讯作者:张梦华

DOI:10.15938/j.emc.2016.06.002

中图分类号:TM 85

文献标志码:A

文章编号:1007-449X(2016)06-0009-08

程新功(1973—), 男，博士，教授，研究方向为电力系统、非线性控制理论；

宗西举(1981—), 男，博士，副教授，研究方向为控制理论与工程；

王洪杰(1988—), 男，助理工程师，研究方向为城市轨道交通供电系统设计；

王玉真(1987—), 男，工程师，研究方向为电力电子。