磁极分段式高速轴向磁通永磁电机转子强度研究

佟文明，　次元平

(沈阳工业大学 国家稀土永磁电机工程技术研究中心， 辽宁 沈阳 110870)



磁极分段式高速轴向磁通永磁电机转子强度研究

佟文明，次元平

(沈阳工业大学 国家稀土永磁电机工程技术研究中心， 辽宁 沈阳 110870)

摘要:为了满足机械强度要求，高速永磁电机通常采用径向磁通结构。随着非晶合金等新型超薄软磁材料的发展，高速高频轴向磁通永磁电机逐步引起关注。为此,针对一种适合于高速运行的磁极分段式轴向磁通永磁电机转子结构进行研究。建立了该转子结构强度解析计算模型，分别利用解析法和有限元法计算了不同极弧因数、转子轮缘宽度以及转子磁极分段数对转子机械强度的影响规律。同时研究了磁极分段式结构对轴向磁通永磁电机气隙磁密、空载反电动势、齿槽转矩和转矩密度等电磁性能的影响。结果证明采用磁极分段式结构能有效提高转子强度，相关研究工作为高速轴向磁通永磁电机的设计提供参考。

关键词:轴向磁通永磁电机；高速；磁极分段；转子支架；机械强度；电磁性能

0引言

开发超高速数控机床是实现超高速加工的物质基础，而高速电主轴电机又是超高速数控机床的核心部件，它的性能直接决定了机床的加工性能。

目前已有大量文献对径向磁通结构高速永磁电机的电磁性能[1-4]、轴承系统[5-6]和转子强度[7-12]展开了卓有成效的研究工作。文献[7]推导了表贴式径向磁通高速永磁电机分块永磁体转子强度的解析表达式，采用解析算法计算碳纤维护套、永磁体的应力，并用有限元法进行了验证。文献[8]分别利用解析法和有限元法对带护套表贴式径向磁通高速永磁电机转子强度进行了计算，并给出了一台额定转速为60 000 r/min永磁电机转子强度计算结果。文献[9]推导了两层过盈配合、三层过盈配合转子应力、应变、位移的解析公式，并用有限元验证了解析计算的正确性。文献[10]针对一台100 kW，60 000 r/min的表贴式高速永磁电机设计了合金材料和碳纤维保护两种保护措施，并分别计算了在静止、冷态运行和热态运行等工况下的转子应力。文献[11]推导了高速内置式永磁电机在离心力作用下转子隔磁桥最大应力的解析计算模型，并通过有限元计算验证了解析推导的正确性，在此基础上，分析了永磁体分段对转子强度和空载漏磁因数的影响，得出将永磁体沿圆周方向进行分段可有效减小隔磁桥的最大应力。文献[12]采用等效环法对内置式永磁转子应力进行解析计算，建立了隔磁磁桥厚度与最高转速的数学关系式，并用有限元法分析了内置式转子的应力分布。对于轴向磁通高速永磁电机转子强度的研究资料相对较少。文献[13]采用有限元法计算了一台16 000 r/min轴向磁通永磁电机的转子应力分布，该电机转子采用永磁体粘接在转子盘表面的结构。文献[14]提出了一种高速轴向磁通永磁电机转子结构，该转子沿径向分层，在永磁体外围增加了一层高强度保护环，该结构相对复杂，且与常规径向磁通高速永磁电机的结构工艺和分析方法相类似。

综上所述，目前已有高速永磁电机研究成果主要针对于径向磁通结构，所采用的转子结构通常是在永磁体外部加入高强度合金或碳纤维护套。由于高速电主轴的转速可能高达25 000 r/min以上，因而频率可达几百甚至上千赫兹，普通硅钢片电机在如此高频下工作会导致电机的铁耗很大、发热严重，进而影响电机性能和加工精确度，采用新型非晶合金材料代替常规硅钢能有效降低高频电机铁耗[15-16]。由于非晶合金薄、脆、硬的特性，更适合做成具有卷绕铁心的轴向磁通结构，槽部可通过铣削或线切割加工得到，为此，需要研究结构工艺相对简单、可靠性高的高速轴向磁通永磁电机转子结构。

本文针对一种适合高速运行的磁极分段式轴向磁通永磁电机转子结构进行研究，通过将每个转子磁极沿圆周方向进行分段来改善转子强度、提高极限工作转速。建立了该结构电机转子支架受力解析计算模型，通过解析法和有限元法计算了极弧因数、轮缘宽度和辐条数对转子支架受力的影响规律。最后以一台15 kW，25 000 r/min的轴向磁通永磁电机为例，分析了磁极分段式结构对转子强度和电机电磁性能的影响规律。

1电机结构

所分析的电机模型如图1所示，为双定子单转子结构，永磁体嵌入转子支架当中。该结构转子最大受力部位出现在转子支架，可以有效保护永磁体。

图1　轴向磁通永磁电机模型Fig.1　Model of AFPMM

一个极下转子结构示意图如图2所示，其中图2(a)为永磁体不分段结构，图2(b)为永磁体沿圆周方向分两段时的结构。不分段和分两段时轴向磁通永磁电机的磁通路径剖面图如图3所示。在研究转子磁极分段对机械和电磁性能影响规律的过程中，保证每个磁极的永磁体在分段前后体积相同。

2基本假设和理论

2.1假设

电机在额定运行时，转子除受到重力作用外，还同时受到离心力、电磁力、热应力等多种外力作用。对于所研究的高速轴向磁通永磁电机，在电机高速运行时离心力是转子形变的主要因素[17]。

图2　一个极下转子磁极结构示意图Fig.2　Sketch of rotor pole structure

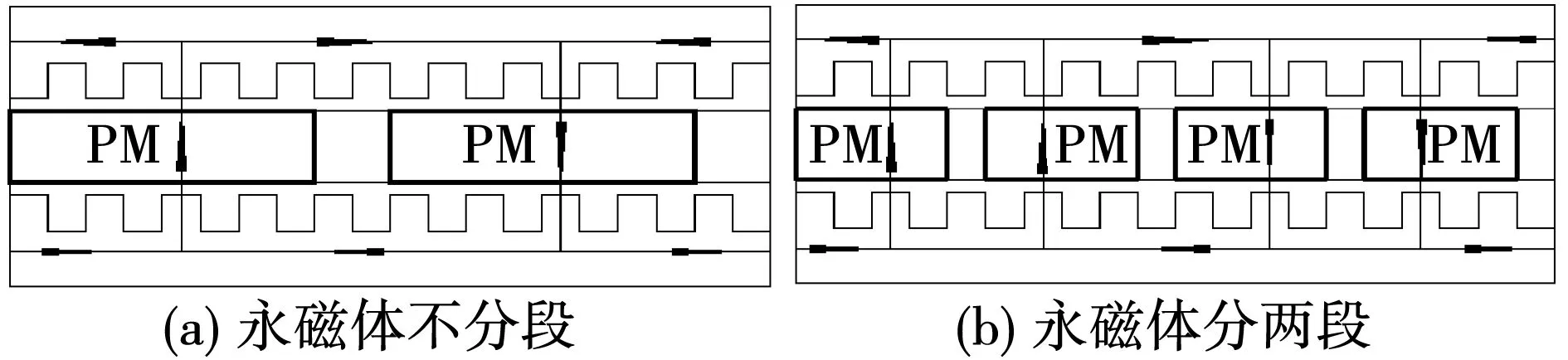
图3　一对极下磁通路径示意图Fig.3　Sketch of magnetic flux path for a pair of poles

对于电机转子机械强度的分析做以下的假设：1)电机高速旋转时的离心力作用远远大于其他因素影响，因而在分析转子强度时仅考虑离心力的作用，而忽略其他作用力；2)只考虑电机在最高转速下稳态运行时转子支架的受力情况；3)忽略温升对转子的影响；4)忽略电机振动的影响[18]。

2.2基本理论

所研究的轴向磁通永磁电机永磁体嵌入在转子支架之中，转子支架为永磁体提供支撑。在电机高速旋转时，转子支架的支撑力抵消永磁体旋转时产生的离心力。为了保证电机能够安全可靠运行，需要研究最极端情况下转子支架的受力情况。

在电机高速旋转时，最极端的情况是永磁体只与轮缘接触，而不与辐条和轮毂相接触。将永磁体和轮缘分成无数个小立方单元，考虑相同半径处小立方体受到的离心力大小相同，假设永磁体、轮缘密度均匀，则每个永磁体或轮缘单元受到的离心力大小可以表示为

dF=ρdVω2r。

(1)

式中：ρ为材料密度；dV为单元体积；ω为角速度；r为半径。

则永磁体与轮缘受到的离心力可表示为

F=∫ρβlω2r2dr

(2)

式中:β为永磁体扇形夹角；l为转子盘轴向长度。

在离心力作用下，电机转子支架不同部位受力情况如图4所示[19]。对于转子轮毂，在忽略电机自身的重量的情况下，只存在辐条对其的拉力，如图4(a)所示，拉力大小为F1。转子辐条受到轮缘和轮毂对其的拉力，分别为图4(b)中的F1和F2。轮缘受到的力如图4(c)所示。

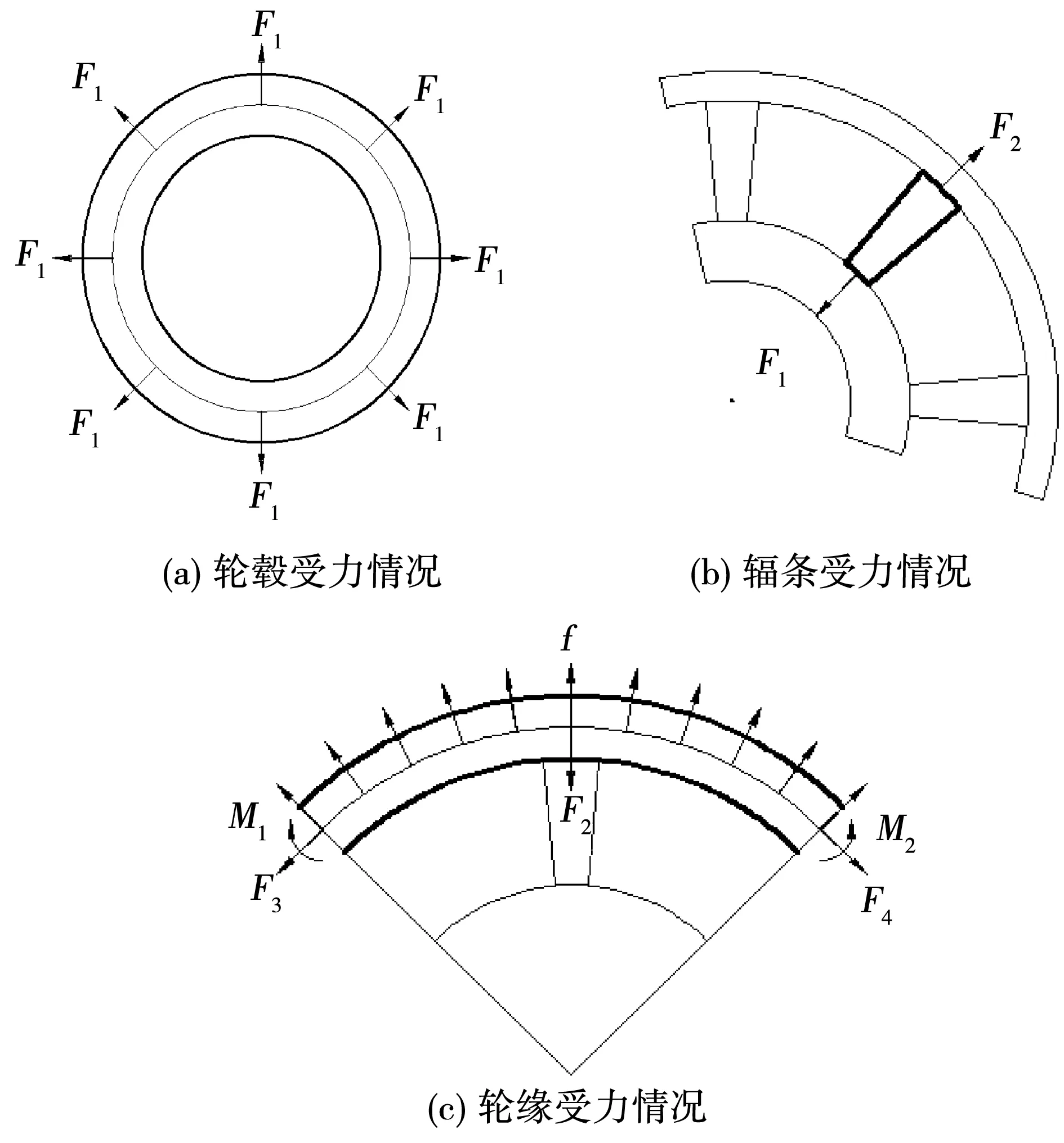
图4　转子支架不同部位受力情况Fig.4　Force analysis at different positions of rotor spider

所研究的转子模型辐条相对较少，可以按照集中应力载荷来计算。转子轮缘是一个曲杆，在电机高速旋转时，轮缘和永磁体因为旋转而受到离心力，使轮缘发生类似蔷薇形的形变[20]。此时在两辐条之间的轮缘将会受到拉力和弯矩的综合作用。同时弯矩的最大值在集中应力的着力点上。

在曲杆弯曲中，由于杆件有一定曲率，其中性线半径一般比中心线半径小。中性线的偏心距为[19]

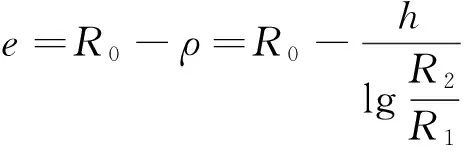
(3)

式中:R0为中性线的半径；ρ为中性线的半径；R2为轮缘的外径；R1为轮缘内径；h为轮缘宽度。

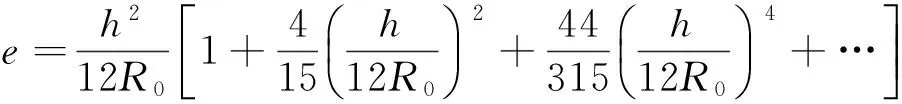
(4)

首先研究转子中只有一对辐条、且两个辐条在同一条直径上的情况。此时，辐条将永磁体分成两个等大的半圆环，每个半圆环对轮缘的压力与轮缘自身产生的离心力之和等效为集中应力，假设集中应力大小为P，则两个应力作用在同一条直径上，根据对称关系，只考虑1/4模型，如图5所示，图中集中应力对此轮缘有向上的拉力。其中mn截面中不存在剪应力，因此垂直于mn平面向下的拉力等于0.5P，同时这个截面有一个待定的弯矩M0，根据卡氏定律可以确定M0。

(5)

式中U为这部分的应变能。

图5　轴向磁通永磁电机转子轮缘受力分析Fig.5　Force analysis of AFPMM rotor flange

任意截面上的拉力Nφ、剪力Qφ和弯矩Mφ为：

(6)

应变能U可以表示为

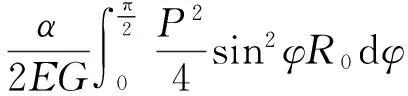
(7)

式中：EI，EF，EG分别为圆环的抗弯强度、抗拉刚度和抗剪刚度；α为材料的剪力截面系数。

经过计算得出Mφ的最终解为

(8)

因此在着力点处的弯矩M1为

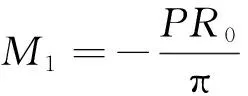
(9)

对于多对集中应力产生的弯矩和纵向拉力可以利用叠加原理进行分析。设M1，N1，M2，N2分别为集中应力着力点上和相邻两个着力点角平分线上的弯矩和拉力，经简化得出各个量的表达式为：

(10)

式中：θ=π/2x；x为辐条个数。

在两个集中应力角平分线上，轮缘内径处的受力为弯矩M2和拉力N2的共同作用产生的[21]。其中弯矩产生的应力为

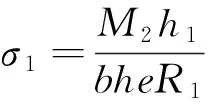
(11)

式中b为转子盘体厚度。

N2在轮缘处产生的应力为

(12)

在两个集中应力角平分线上，轮缘内径处的受力大小为

σ=σ1+σ2。

(13)

3轴向磁通永磁电机机械强度研究

3.1转子材料特性

转子支架与永磁体的物理特性如表1所示。转子支架使用高强度不导磁合金钢。

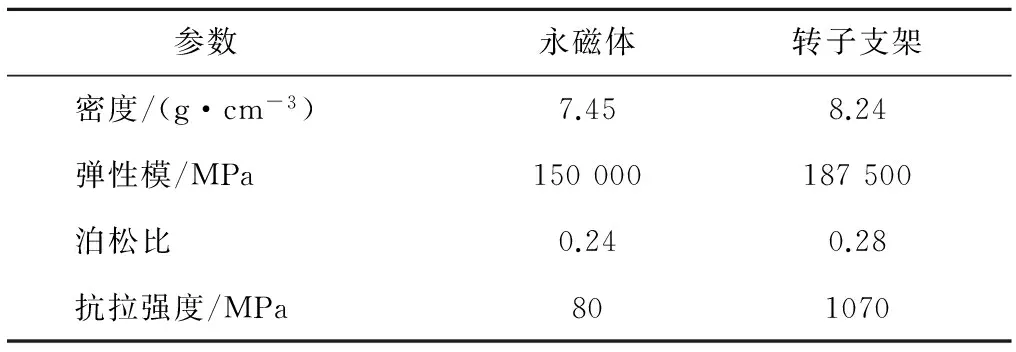
表1　转子支架材料物理特性

3.2有限元验证与规律研究

由解析推导可知，转子支架所受应力与辐条个数、极弧因数以及轮缘宽度有关。以一台15 kW、25 000 r/min的高速轴向磁通永磁电机为例，研究转子支架所受应力随上述因素的变化规律。根据标准考虑电机超速20%，按照30 000 r/min来进行分析计算。在计算过程中，保证永磁体内外径分别为70 mm和110 mm。

高速电机受其本身性能和变频器最高频率的制约，极数一般采用2极或4极。对于2极电机，当辐条数为4时，每极永磁体沿周向分2段；当辐条数为6时，每极永磁体沿周向分3段；当辐条数为8时，每极永磁体沿周向分4段。对于4极电机，当辐条数为8时，每极永磁体沿周向分2段。着重研究辐条数分别为4、6、8时转子的机械强度。

利用解析法和有限元法分别计算了不同辐条数量、极弧因数(从0.75到0.85)和轮缘宽度(从5 mm到10 mm)时转子支架受力情况，有限元计算的应力分布云图分别如图6、图7、图8所示。在分析辐条数量影响时，保持极弧因数(0.75)和轮缘宽度(5 mm)不变；在分析极弧因数影响时，保持辐条数(4)、轮缘宽度(5 mm)不变；在分析轮缘宽度影响时，保持辐条数(4)和极弧因数不变(0.75)。从有限元仿真云图可以看出，无论哪种参数组合，电机转子应力最大值均出现在电机轮缘与辐条连接部位。因此在设计转子支架时要着重分析辐条和轮缘衔接处的应力。

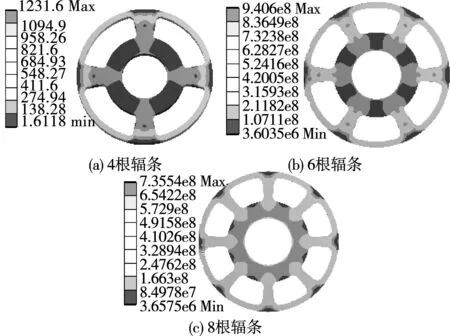
图6　不同辐条数时转子应力分布Fig.6　Rotor stress distributions under different spokes

解析法与有限元法计算结果对比如表2和表3所示。由表可知，解析计算结果的规律性与有限元计算结果相符，但由于解析法无法考虑局部倒圆角的具体结构细节，因而，两种方法计算结果存在一定的差异，但平均计算误差小于8%，解析计算结果满足工程需要。

图7　不同极弧因数时转子应力分布Fig.7　　　　Rotor stress distributions under different　　　 pole arc factors

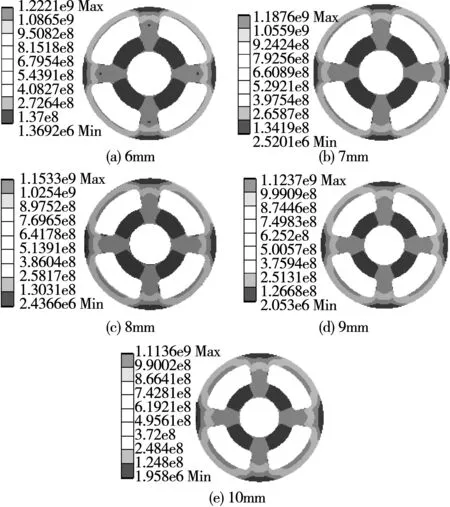
图8　不同轮缘宽度时转子应力分布Fig.8　　　　Rotor stress distributions under different　　　 width of flange

极弧因数4根辐条/MPa6根辐条/MPa8根辐条/MPa解析有限元解析有限元解析有限元0.751343.01231.61028.2940.6727.4735.50.771377.91259.91054.7944.9745.9748.80.791412.91315.01081.5979.2764.8752.80.811447.81347.21108.2983.2783.7760.10.831482.71375.01134.91012.7802.6776.20.851517.61432.71161.61056.1821.5797.6

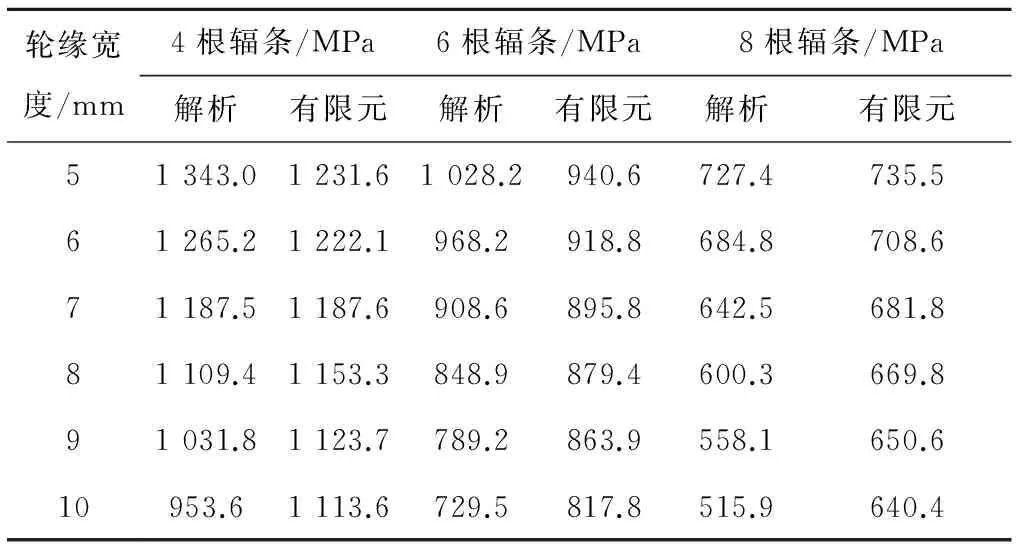
表3　极弧因数为0.75时转子受力最大值

对表2和表3中计算结果进行分析可知，随着辐条数的增加，转子所受应力大幅度减小。从有限元计算结果来看，辐条数由4增加到6，转子支架所受最大应力平均减小25.02%，当辐条数增加到8时最大应力平均减小42.21%。由此可见，采用永磁体分段来增加高速轴向磁通电机转子盘体辐条数量的方法可以显著提高电机的转子机械强度。

与增加转子辐条数相比，改变转子轮缘宽度和极弧因数对电机转子机械强度影响相对较小。从计算结果来看，当极弧因数和转子辐条数不变时，随着转子轮缘宽度的增加，电机的转子机械强度逐渐改善，转子受到的应力和轮缘宽度近似呈线性关系。当转子轮缘宽度每增加1 mm，其所受应力大约减小约2.50%；当轮缘宽度从5 mm增加到10 mm时，转子应力平均减小约11.86%。

当轮缘宽度和转子辐条数不变时，转子支架最大应力随极弧因数的增加近似线性增大。极弧因数每增加0.2，转子所受应力约增大2.36%；当极弧因数从0.75增到0.85时，转子应力增大约12.35%。

415 kW、25 000 r/min电机性能分析

4.1电机参数

对一台15 kW、25 000 r/min高速轴向磁通永磁电机进行了转子结构设计，根据前面分析，为了改善转子强度，电机的极弧因数设计为0.75，转子轮缘宽度为10 mm，该电机参数如表4所示。

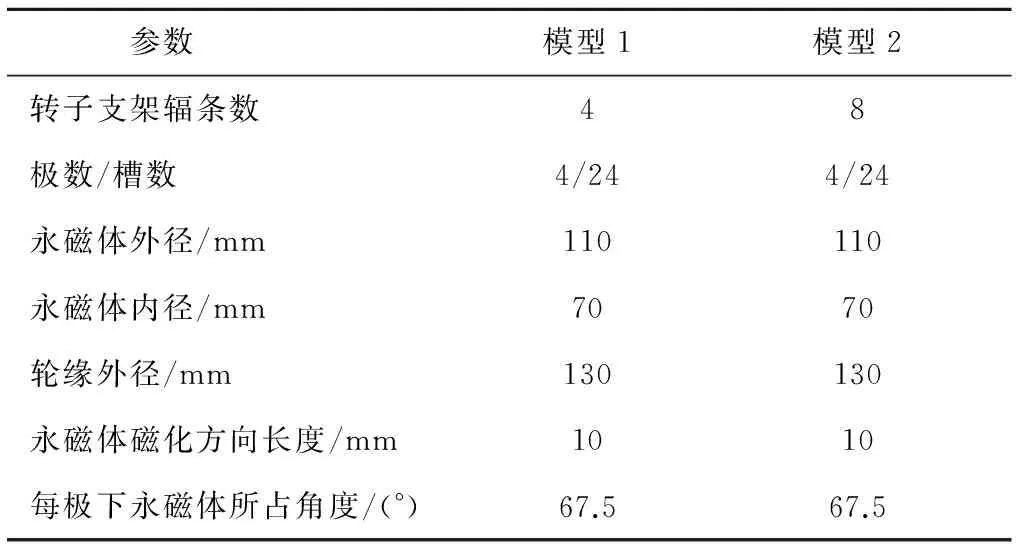
表4　轴向磁通电机模型参数

4.2强度分析

对在永磁体不分段和分两段时机械和电磁性能进行分析，转子支架受力云图如图9所示。由图中可以看到当转子支架辐条数为4时，支架受到的最大应力为1 113.6 MPa，非常接近材料的抗拉强度。而当辐条数为8时，最大应力减小到4根辐条时的58.87%，仅为655.6 MPa，此时安全系数为1.63，能够满足电机机械强度要求。

由此可见，采用磁极分段式结构、同时合理设计极弧因数和轮缘宽度，可以有效提高高速轴向磁通永磁电机的转子机械可靠性。

图9　不同辐条数量时转子应力Fig.9　Rotor stress at different spokes

4.3电磁性能分析

永磁体分段不可避免地会对电机的电磁性能产生影响。为了定量研究其影响程度，对表4中转子支架辐条数分别是4和8的两台轴向磁通永磁电机的电磁性能进行分析，主要分析永磁体分段前后电机每极气隙磁场空间分布、空载反电动势波形大小与畸变率、齿槽转矩和电机转矩密度的变化情况。表4中所列的两台电机具有相同的定子结构和尺寸参数，每极永磁体面积相同，区别仅在于转子支架辐条数分别是4和8，即一台电机永磁体不分段，而另一台电机每极永磁体分两段。

通过三维电磁场分析，计算得到一个磁极下两台电机气隙磁密三维空间分布情况，如图10所示。

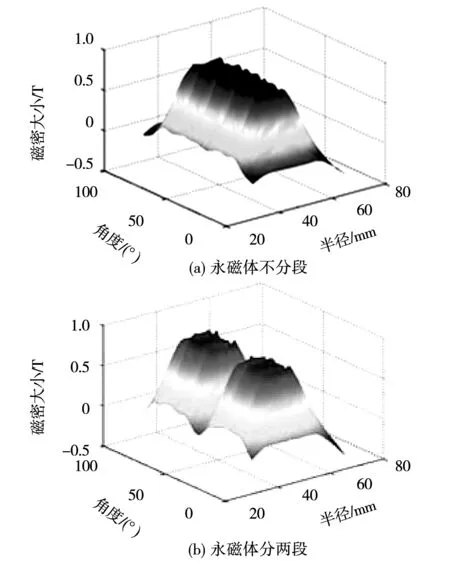
图10　一个磁极下气隙磁密分布Fig.10　Air gap flux density distribution under a pole

从图中可以看出，当永磁体不分段时，电机气隙磁密沿圆周分布近似为平顶波(忽略齿槽效应)。而当一个磁极下永磁体分两段时，电机气隙磁密沿圆周分布不均匀，在两块相同极性永磁体中间辐条对应的位置出现一个较大的下凹区域，该位置的气隙磁密接近于零。分别选取两台电机在半径45 mm处一个磁极下的气隙磁密波形进行傅里叶分析得到永磁体不分段时气隙磁密基波幅值为0.91 T，波形畸变率为24.08%；而当永磁体分两段时，气隙磁密基波幅值降为0.82 T，下降幅度为9.89%，波形畸变率达到61.34%。由此可见，永磁体分段对气隙磁密幅值和波形均产生了较大影响。通过三维瞬态电磁场仿真，得到在额定转速下电机的空载反电动势和齿槽转矩随时间变化曲线，如图11、图12所示。当永磁体不分段时，空载反电动势有效值为378.0 V，波形畸变率为11.98%，齿槽转矩为0.43 N·m；而永磁体分两段后，空载反电动势有效值变为336.6 V，波形畸变率为13.55%，齿槽转矩则变为1.39 N·m。由此可知，尽管分段前后空载反电动势的波形畸变率变化不大，但分段之后空载反电动势有效值约减小了11%，齿槽转矩则增大了2.23倍。因此，尽管分段会大大提高电机的转子机械强度，但同时导致电机的空载气隙磁密波形畸变率大幅增加、电机的空载反电动势有所下降、且齿槽转矩幅值大幅增大。电机在永磁体分段前后的性能参数汇总如表5所示。

图11　两种情况空载反电动势波形Fig.11　No-load back EMF waveforms in both cases

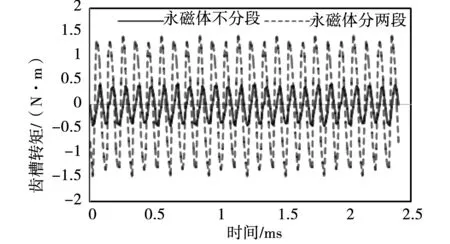
图12　两种情况齿槽转矩对比Fig.12　Comparison of cogging torque in both cases

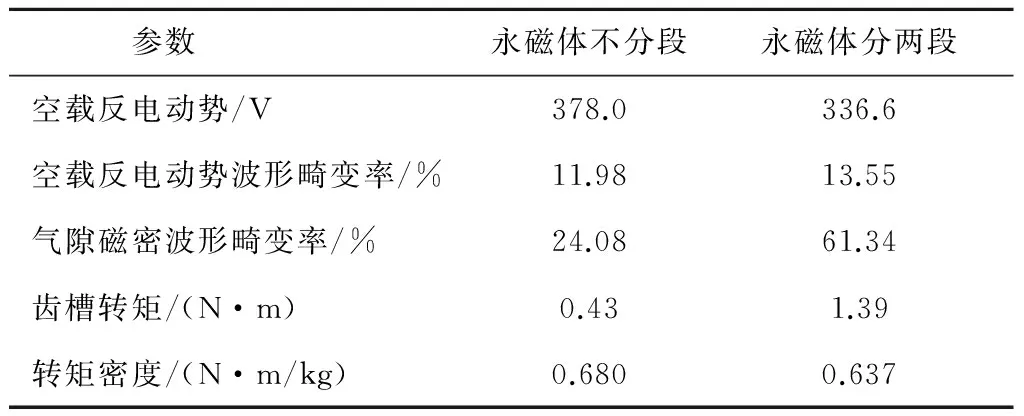
参数永磁体不分段永磁体分两段空载反电动势/V378.0336.6空载反电动势波形畸变率/%11.9813.55气隙磁密波形畸变率/%24.0861.34齿槽转矩/(N·m)0.431.39转矩密度/(N·m/kg)0.6800.637

由于分段后由永磁体产生的空载气隙磁密的谐波成分大幅增大而基波成分有所减小，进而导致空载反电动势减小、永磁材料利用率下降，这进一步引起电机转矩密度的降低。在相同的冷却条件下(保证永磁体分段前后电机具有相同的电磁负荷，各发热部位的发热量近似相等)，对比了永磁体不分段与分两段时电机的转矩密度，如表5所示，从表中可知，永磁体分段后电机的转矩密度降低了6.32%。

除此之外，永磁体分段对轴向磁通永磁电机的杂散损耗(尤其是由于永磁体谐波磁场在定子铁心中引起的损耗)会产生一定影响。对高速非晶合金永磁电机而言，由于非晶合金材料损耗很小，因而定子铁心的损耗并不显著，永磁体的谐波磁场对电机损耗的影响并不突出；同时，为了保证高速电机的转子机械强度性能，考虑到高速电机本身体积很小，因而转矩密度下降6.32%带来的影响是可接受的。但是对齿槽转矩和转矩波动要求较高的场合，在考虑对永磁体分段时要谨慎，并且需要进行必要的改进与优化。

5结论

本文针对一种适合高速运行的磁极分段式轴向磁通永磁电机的机械和电磁性能进行研究，得出以下结论：

1)对于本文所研究的高速轴向磁通永磁电机转子结构，采用磁极分段式结构可以大大减小转子支架所受的最大应力，以分两段为例，与不分段相比转子支架最大应力减小约42%。但是，磁极分段会导致气隙磁密波形变差，齿槽转矩大幅增大，转矩密度所有降低。

2)与增加转子辐条数相比，转子轮缘宽度和极弧因数对电机转子机械强度影响相对较小。转子受到的应力随轮缘宽度增大近似呈线性减小；随极弧因数的增加近似线性增大。

参 考 文 献:

[1]王继强, 王凤祥, 孔晓光.高速永磁发电机的设计与电磁性能分析[J].中国电机工程学报, 2008, 28(20): 105-110.

WANG Jiqiang,WANG Fengxiang, KONG Xiaoguang. Design and analysis of electromagnetic properties for high speed PM generator[J].Proceedings of the CSEE, 2008, 28(20): 105-110.

[2]孔晓光, 王凤翔, 徐云龙, 等.高速永磁电机铁耗分析与计算[J]. 电机与控制学报, 2010, 14(9): 26-30.

KONG Xiaoguang, WANG Fengxiang, XU Yunlong, et al.Analysis and calculation of iron losses of high-speed permanent magnet machines[J].Electric Machines and Control, 2010, 14(9): 26-30.

[3]孔晓光, 王凤祥, 邢军强. 高速永磁电机的损耗计算与温度场分析[J]. 电工技术学报, 2012, 9(27): 166-173.

KONG Xiaoguang, WANG Fengxiang, XING Junqiang. Losses Calculation and Temperature Field Analysis of High Speed Permanent Magnet Machines[J].Transactions of China Electrotechnical society, 2012, 9(27): 166-173.

[4]CHEBAK A, VIAROUGE P, CROS J. Optimal design of a high-speed slot-less permanent magnet synchronous generator with soft magnetic composite stator yoke and rectifier load[J]. Mathematics and Computers in Simulation, 2010, 81(2):239-251.

[5]田拥胜, 孙岩桦, 虞烈.高速永磁电机电磁轴承转子系统的动力学及实验研究[J].中国电机工程学报, 2012,32(9):116-123.

TIAN Yongsheng, SUN Yanhua, YU Lie. Dynamical and experimental researches of active magnetic bearing rotor systems for high-speed PM machines[J]. Proceedings of the CSEE, 2012, 32(9): 116-123.

[6]王继强, 王凤翔, 宗鸣. 高速电机磁力轴承—转子系统临界转速的计算[J].中国电机工程学报, 2007, 27(27): 94-98.

WANG Jiqiang, WANG Fengxiang, ZONG Ming. Critical speed calculation of magnetic bearing-rotor system for a high speed machine[J]. Proceedings of the CSEE, 2007, 27(27): 94-98.

[7]王保俊, 刘毕新, 段亮亮, 等. 碳纤维绑扎表贴式高速永磁电机转子强度分析[J]. 浙江大学学报, 2013, 47(12): 2101-2110.

WANG Baojun, LIU Bixin, DUAN Liangliang, et al. Strength analysis of a surface mounted high speed permanent magnetic machine rotor with carbon fiber bandage[J]. Journal of Zhejiang University, 2013, 47(12): 2101-2110.

[8]王继强, 王凤祥, 鲍文博, 等. 高速永磁电机转子设计与强度分析[J].中国电机工程学报, 2005, 25(15): 140-145.

WANG Jiqiang, WANG Fengxiang, BAO Wenbo, et al.Rotor design and strength analysis of high speed permanent magnet machine[J]. Proceedings of the CSEE, 2005, 25(15): 140-145.

[9]程文杰, 耿海鹏, 冯圣, 等. 高速永磁同步电机转子机械强度分析[J]. 中国电机工程学报, 2012, 32(27): 87-94.

CHENG Wenjie, GENG Haipeng, FENG Sheng, et al. Rotor strength analysis of high-speed permanent magnet synchronous motors[J]. Proceeding of the CSEE, 2012, 32(27): 87-94..

[10]张凤阁, 杜光辉, 王天煜.高速永磁电机转子不同保护措施的机械强度分析[J]. 中国电机工程学报, 2013, 33(zl): 195-202.

ZHANG fengge, DU Guanghui, WANG Tianyu, et al. Rotor strength analysis of high-speed permanent magnet under different protection measure[J]. Proceeding of the CSEE, 2013, 33(zl): 195-202.

[11]佟文明, 次元平. 高速内置式永磁电机转子机械强度研究[J]. 电机与控制学报, 2015, 19(11): 45-50.

TONG Wenming, CI yuanping. Study on rotor mechanical strength of a high speed interior permanent magnet motor [J]. Electric Machines and Control, 2015, 19(11): 45-50.

[12]张涛, 朱熀秋, 孙晓东，等.基于有限元法的高速永磁转子强度分析[J]. 电机与控制学报, 2012, 16(6): 63-68.

ZHANG Tao, ZHU Huangqiu, SUN Xiaodong, et al. Strength analysis on high-speed permanent magnet rotor using finite element method[J]. Electric Machines and Control, 2012, 16(6): 63-68.

[13]SAHIN F. Design and development of a high-speed axial-flux permanent magnet machine[D]. Eindhoven: Eindhoven University of Technology, 2001.

[14]FEI W,LUK P C K,ELHASAN T S.Rotor integrity design for a high-speed modular air-cored axial-flux permanent-magnet generator[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9):3848-3858.

[15]朱龙飞, 朱建国, 佟文明, 等. 非晶合金永磁同步电机空载损耗[J]. 电机与控制学报, 2015, 19(7): 21-26.

ZHU Longfei, ZHU Jianguo, TONG Wenming, et al. Study on no-load losses of permanent magnet synchronous motor with amorphous alloy stator core[J]. Electric Machines and Control, 2015, 19(7): 21-26.

[16]佟文明, 朱晓锋, 朱龙飞, 等. 不同供电方式对非晶合金永磁同步电机铁耗的影响[J]. 电工技术学报, 2015, 30(10): 115-122.

TONG Wenming, ZHU Xiaofeng, ZHU Longfei, et al. Study on the impact of different supply modes on core losses of amorphous alloy permanent magnet synchronous motor[J].Transactions of China Electrotechnical society, 2015, 30(10): 115-122.

[17]陈远扬, 韩则胤, 陈阳生.高速内嵌式永磁电动机转子机械强度分析[J].微特电机, 2012, 40(5): 5-9.

CHEN Yuanyang, HAN Zeyin, CHEN Yangsheng. Mechanical strength analysis of high speed interior permanent magnet motor[J].Small & Special Electrical Machines, 2012, 40(5): 5-9.

[18]EDWARD C L, THOMAS M J, THOMAS A K, et al. Mechanical design considerations for conventionally laminated, high-speed, interior PM synchronous machine rotors[J]. IEEE Transactions on Industry Applications, 2004, 40(3):806-812.

[19]钱伟长.电机设计强度计算的理论基础[M].合肥:安徽科学技术出版社, 1992: 41-61.

[20]卡拉索夫斯基.电机强度问题[M].关力更译. 北京: 机械工业出版社, 1959: 34-37.

[21]戴葆青, 王崇革, 付彦坤. 材料力学教程[M]. 北京: 北京航空航天大学出版社, 2004: 194-200.

(编辑：贾志超)

Rotor strength of high speed axial flux permanent magnet machine with segmented rotor pole structure

TONG Wen-ming,CI Yuan-ping

(National Engineering Research Center for Rare-earth Permanent Magnet Machines,Shenyang University of Technology, Shenyang 110870, China)

Abstract:In order to meet the requirements of mechanical strength, radial flux structure is always adopted in high-speed permanent magnet motor. With the development of ultra-thin soft magnetic materials, such as amorphous alloy, high-speed high-frequency permanent magnet motor with axial flux structure is drawing more and more concern. Therefore, a kind of axial flux permanent magnet motor (AFPMM) with segmented rotor pole structure that is suitable for high-speed operation was studied. An analytical model was built to evaluate the mechanical strength of this type of rotor. Both analytical method and finite element method were used to study the influence law of rotor strength under different pole arc factors, flange width of rotor, and number of segments of each rotor pole. Meanwhile, the influence law of segmented rotor pole structure on the electromagnetic performances of AFPMM, such as air gap flux density, no-load back EMF, cogging torque and torque density was studied. The research work provides a reference for the development of high-speed AFPMM.

Keywords:axial flux permanent magnet motor; high speed; segmented rotor pole; rotor spider; mechanical strength; electromagnetic performance

收稿日期:2015-05-14

基金项目：国家自然科学基金(51307111)；国家科技支撑计划项目(2013BAE08B00)；辽宁省教育厅科学技术研究项目(L2013049)

作者简介：佟文明(1984—)，男，博士，副教授，硕士生导师，研究方向为特种电机及其控制与电机多物理场仿真分析； 次元平(1988—)，男，硕士，研究方向为高速电机机械强度分析与电磁设计。

通讯作者:佟文明

DOI:10.15938/j.emc.2016.06.009

中图分类号:TM 315

文献标志码:A

文章编号:1007-449X(2016)06-0068-09