基于Trilinos开发的并行复杂几何Poisson方程求解器

王虹宇

(鞍山师范学院 物理科学与技术学院,辽宁 鞍山 114007)



基于Trilinos开发的并行复杂几何Poisson方程求解器

王虹宇

(鞍山师范学院 物理科学与技术学院,辽宁 鞍山 114007)

摘要基于Trilinos程序包中的AztecOO和ML package开发了并行Poisson求解器.在非均匀的结构化网格上实现了复杂金属/电介质几何体的建模.Poisson方程通过有限体积方法离散形成求解矩阵，然后利用Trilinos进行并行矩阵求解.并行测试表明，求解器的收敛表现良好，在典型情况下性能满足需求.这一求解器代码可以用于从等离子体模拟到传热过程等多种任务.

关键词Trilinos；Poisson方程；复杂几何

在许多问题中，都需要在一个带有金属电极和电介质的区域中求解静电场问题.这归结为求解下面的Poisson方程：

将这个方程通过有限元或者有限差分/有限体积方法进行离散，形成一个极度稀疏的线性方程组,然后使用数值线性代数方法进行求解[1].

尽管上述方法的理论概念是直截了当的，但实际执行中存在一系列问题.首先是在工程问题中金属电极和介质的几何外形都会很复杂，因此上述方程的离散形式可能存在一系列误差(特别对于有限差分离散的情况)，而且标准的谱方法和本征函数展开(分离变量)等方法都不适用；其次形成的线性方程组的维度是N*N的，N是离散单元的个数，对于三维问题，N很容易达到107甚至更多.这样庞大的线性方程组只能使用并行计算机求解；最后，Poisson方程本质上是高度病态的，极易出现慢收敛甚至不收敛行为.

在以前的工作中，我们发展了多个基于规则网格上的Poisson方程的等离子体Particle-In-Cell程序.其中包含一系列Poisson方程快速求解器的实现[2～5].但这些求解器普遍不考虑复杂外形的金属电极.近期，我们在卫星表面充电的仿真研究中，需要考虑包含复杂几何体(金属和/或介质)情况下的Poisson方程求解.在这种情况下，前面提到的求解器都要做较大规模的修改.考虑到工程实践的需求，我们重构了规则网格上的Poisson方程离散形式，并将矩阵求解器内核替换为sandia实验室的Trilinos库[6]，测试结果表明在大部分工程问题中这种简化的求解器是可以满足需求的.

1Poisson方程的离散

对于包含复杂几何体的情况，电磁场问题的求解可以使用两种类型的网格：结构网格或者非结构网格.有限元软件通常使用非结构网格，而FDTD或者FDM软件常常使用结构网格.目前，Particle-In-Cell代码在非结构网格上的实现仍然存在一些困难，因此我们使用结构网格，并将复杂物体的曲面边界用阶梯近似来逼近.对于静电问题，由于电势本质上是光滑的，因此阶梯近似带来的误差并不大，而一些形状特殊的细部精度问题可以使用局部的加密网格来解决.

将整个模拟空间设置为一个LX*LY*LZ的长方体，然后在3个坐标方向分别实现坐标网，然后形成三维网格：

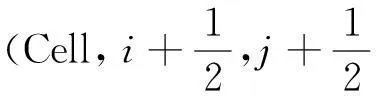
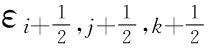
每个节点都定义一个Φi,j,k值，如果这个节点属于空间或介质，利用高斯定理写出

其中，使用到棱心电场

以及垂直棱边的单元面积

棱心的介电常数从围绕的4个体心加权平均得出

其余类推.

如果这个节点属于金属m，那么直接写出其电势方程为Φi,j,k=Vm，这样就得出一系列关于Φi,j,k的线性方程组.由于对金属和介质节点的不对称处理，这个线性方程组的矩阵不是对称的.

2Trilinos矩阵的装配

Trilinos是由sandia国家实验室开发的一个矩阵计算程序库，包含从简单的稀疏矩阵计算到特征值处理的各种数据库，其大部分接口都已经封装成C++形式，可以简单地在程序中调用.在这里需要的主要分布式向量矩阵模块Epectra，矩阵迭代器AztecOO和预条件库ML.

Epectra的主要作用是建立分布式的向量和稀疏矩阵.由于求解在分布式存储的集群上进行，待求解的Φ也必须被分布存储.将整个模拟网格进行规则分解，每个进程负责分解后的一个长方体分块.将第s进程中存储的格点标记为

于是这个进程中存储的格点总数为rankElements=LsMsNs.对每个节点定义一个全局标号Tg(i,j,k)和一个在本进程中的标号Tl，这两者是一一对应的：对于第一个进程(rank 0),Tl从0顺序排列到L0M0N0-1而Tg=Tl;对于第二个进程，Tl仍然是0到L1M1N1-1，而Tg是L0M0N0到L0M0N0+L1M1N1-1，以此类推.按照这种分割描述，建立Epectra映射:

Epetra_Map PhiA(-1,rankElements,0,Comm);

这样就建立了一个分布存储在s=0到s=Nprocs进程内的向量的框架.然后直接通过拷贝建构来产生同样结构的Φ和ρ向量：

Epetra_Vector x(PhiA);

Epetra_Vector b(PhiA);

Trilinos提供的主要功能是求解方程Ax=b.由于上面的Poisson矩阵是七点形式，所以建立一个最多7点的稀疏矩阵：

Epetra_CrsMatrix MatrixA(Copy,PhiA,7);

MatrixA初始的时候元素都是0，以后顺序添加非零元素：对每个进程，遍历本进程负责的全部局部标号Tl，设其对应的全局标号为Tg= global_row,那么可以使用下面的代码：

MatrixA.InsertGlobalValues(global_row,1,&Coefficients[0],&global_row);

global_row是矩阵A对应Tg的行号，而InsertGlobalValues将Coefficients[0]插入到这一行的相应列，现在因为第4个参数实际就是global_row，所以插入的位置就是这一行的对角元.

同理，对于其他6个非零系数，都可以进行全局插入，例如，左方(i-1方向)元素的全局编号为global_left，那么插入代码为

MatrixA.InsertGlobalValues(global_row,1,&Coefficients,&global_left);

这样，只要计算了6个非零系数的局部和全局标号，就可以正确生成矩阵的这一行.对于空间和介质网格，7个非零矩阵元素从前面公式算出然后插入，对于金属网格以及第一类边界条件，只要插入对角元素1即可.遍历所有格点就生成了矩阵A.最后用MatrixA.FillComplete()结束矩阵的装配.

方程右端项b是和待求解格点一一对应的分布式数组，按照前述公式，对于金属格点，设置对应点的b值等于电势；对于介质和空间，将b值设置为这个节点电荷密度乘以

3ML preconditioner装配和求解

由于生成的线性方程组维度太大，需要进行迭代求解，这里使用通用性较好的gmres方法.但直接用原始的gmres方法迭代求解的性能仍然不能满足要求，需要使用预条件.在Poisson-like方程的情况下，一般认为代数多重网格的效果比较好[7].Trilinos的ML程序包提供了代数多重网格预条件，测试表明，可以直接使用这个预条件并且用AztecOO中设置好的gmres方法求解相应矩阵：

void TrilinosSolver(Epetra_CrsMatrix& MatrixA,Epetra_Vector& x,Epetra_Vector& b)

{

Epetra_LinearProblem problem(&MatrixA,&x,&b);

AztecOO solver(problem);

ML_Epetra::MultiLevelPreconditioner * MLPrec = new ML_Epetra::MultiLevelPreconditioner(MatrixA,true);

solver.SetPrecOperator(MLPrec);

solver.SetAztecOption(AZ_solver,AZ_gmres_condnum);

solver.SetAztecOption(AZ_output,128);

solver.SetAztecOption(AZ_kspace,160);

int Niters = 500;

solver.Iterate(Niters,1e-8);

delete MLPrec;

}

4模型算例

使用了一个具有多个部件的物体测试我们的代码.模拟物体的形状如图1，上面3个相连的同轴圆柱体构成了金属部分，最大圆柱体半径是1 m，下方的长方体是边长2 m*2 m*0.2 m，介电常数为3的电介质实体.金属体被充电到100 V，然后整个物体被放入4 m见方的立方体空间中，计算边界为简单Dirichlet条件.

对几何建模进行网格剖分的大致效果如图2.我们使用了64*64*64和100*100*100两种网格进行验证.图3中给出了64*64*64网格剖分后求解的电场X-Z剖面等势线，金属体和介质对电场的影响可以很容易地看出.100*100*100网格的求解效果与之类似.

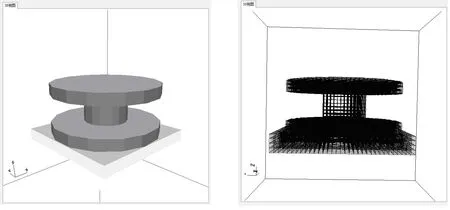
图1　金属部件模型　　　　　　　　　图2　网格剖分的样例

并行效率测试见图4，虚线和实线分别代表64*64*64和100*100*100网格的执行效能(执行时间的倒数).结果表明，由于ML preconditioner本身的特性，随着使用进程数的增加，加速比逐步下降.尽管如此，由于64*64*64和100*100*100的网格在8路并行上对应的平均求解时间只有0.11 s和0.55 s左右，对于大部分工程问题已经基本可以满足需求.对于更复杂的问题，可以通过更多(数百路)的并行给出满意的结果.

5结论

针对工程中一类典型问题的需求，我们利用Sandia的Trilinos程序包实现了包含复杂几何的金属体和电介质的静电问题的求解器子程序.近期我们将这一程序应用于卫星在电离层中充电的研究中，获得了基本满意的结果.

由于Poisson问题的求解是一大类计算物理问题(如不可压流动问题，传热问题等等)中必须的内容，而这个求解器程序构建和重构都非常简单，预期可以应用于更多领域.

目前求解器建模还只包含各向同性介电函数和规则网格阶梯近似的情况.未来我们将发展包含各向异性介电和局部共形(或者Cut-Cell)结构的求解器代码.

图3　切面上的电势分布　　　　　　　　图4　并行效率测试结果

参考文献

[1] Birdsall C K，Langdon A B.Plasma Physics via Computer Simulation[M].New York:McGraw-Hill,1985.

[2] Wang H Y,Jiang W,Wang Y N.Parallelization and optimization of electrostatic Particle-in-Cell/Monte-Carlo Coupled codes as applied to RF discharges[J].Comput Phys Commun,2009,180(8):1305-1314.

[3] Wang H Y,Jiang W,Wang Y N.Implicit and electrostatic particle-in-cell/Monte Carlo model in two-dimensional and axisymmetric geometry:I.Analysis of numerical techniques[J].Plasma Source Sci Tech,2010,19(4)：045023.

[4] Wang H Y,Jiang W,Sun P,et al.Implicit electrostatic particle in cell/Monte-Carlo simulation for the magnetized plasma:algorithms and verifying in gas inductive breakdown [J].Chin Phys B,2015,24(6):433.

[5] 王虹宇.一类用于光滑系数的轴对称静电问题的半粗化多重网格方法[J].鞍山师范学院学报,2010，12(6)：33-37.

[6] Heroux M,Bartlett R,Howle V,et al.An Overview of Trilinos[R].Tech-Report,SAND,2003-2927.

[7] Trottenberg U,Oosterlee C,Shuller A,et al.Multigrid[M].New York:Academic,2001.

(责任编辑：陈欣)

A parallel poisson solver with cmplex gometry developed with trilinos

WANG Hongyu

(School of Physical Science and Technology,Anshan Normal University,Anshan Liaoning 114007,China)

AbstractA Poisson Solver based on AztecOO and ML in Trilinos is developed.The metal and dielectric object with complex geometry is modeled in a non-uniform structure grid.Poisson equation is discretized by finite volume method to build a sparse matrix.The sparse matrix is solved paralleled with Trilinos.The benchmark show good convergence rates and satisfying performance.This solver code can be used for kinds of problem as plasma simulating and heat transfer.

Key wordsTilinos；Poisson Solver；complex geometry

收稿日期2016-03-05

作者简介王虹宇(1975-)，男，满族，辽宁沈阳人，鞍山师范学院物理科学与技术学院教授，博士.

中图分类号O441.1

文献标识码A文章篇号1008-2441(2016)02-0028-05