麦蚜种群广义系统模型的突变现象分析

韩立红，赵立纯，刘敬娜

(1.辽宁师范大学 数学学院,辽宁 大连 116029;2.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)



麦蚜种群广义系统模型的突变现象分析

韩立红1,2，赵立纯2，刘敬娜2

(1.辽宁师范大学 数学学院,辽宁 大连 116029;2.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)

摘要麦蚜种群的突变现象一直受到人们的关注,本文基于麦蚜种群广义系统模型,利用广义系统模型的障碍点分析和揭示了麦蚜种群发生突变的生态学机制.最后通过数值仿真验证了结论的正确性.

关键词麦蚜种群；突变现象；广义系统；障碍点

麦蚜种群的爆发严重影响小麦的产量,赵慧燕、吴问其、Piyaratne M.K.D.K等,先后考虑各种生物因素对麦蚜种群的影响,分别建立了尖角突变模型、折叠突变模型、燕尾突变模型、蝴蝶突变模型,来研究麦蚜种群的突变现象[1～4].上述研究皆是从微分方程角度建立相应的模型.随着经济的快速发展,人类活动对生态系统的影响愈发复杂,微分方程刻画的模型已不能满足学者们的需要,由微分方程和代数方程构成的广义系统模型得以进入生态学领域,为此本文在文献[5]所建模型的基础上,通过广义系统模型障碍点的分析,揭示麦蚜生态系统中的突变现象.

1预备知识

考虑麦蚜种群广义系统模型[5]

(1)

其中，x为作物种群的种群密度,r1为作物种群的内禀增长率,k1为作物种群环境容纳量,c为麦蚜种群捕食饱和率，y为麦蚜种群的种群密度,r为麦蚜种群的内禀增长率,d为麦蚜种群的死亡率,p为天敌种群的种群密度,a为麦蚜种群天敌捕食饱和率,b为作物种群对麦蚜种群的影响系数.

设

根据生物含义在Φ上研究模型(1)中麦蚜种群和作物种群之间的相互影响作用.

在文献[5]中已经对该模型的平衡点的稳定性进行分析,本文利用模型的障碍点来分析麦蚜生态系统中的突变现象.为此先介绍障碍点的定义.

定义1[6]若点(x0,y0)是模型(1)的后向障碍点(或向前障碍点),当且仅当(1)(x0,y0)是一个动态操作点,即g(x0,y0);(2)(y0,0)是诱导解曲线Ψ的左极限点(或右极限点).

2突变现象分析

通过下面算法可知道模型(1)是否存在障碍点：

第一步:求其奇异点,为此令

得奇异点

由上得定理1.

定理1对于模型(1),如果ap-rd>0成立，则模型在

有奇异点M0(x0,y0).

第二步:模型(1)的奇异点M0(x0,y0)是否能成为障碍点,为此令

由h(y,λ)=0, 得(y0,λ0)是其解,其中，λ0=0.

对于(y0,λ0)有,

则(y0,λ0)是h(y,λ)的奇异点.

第三步:对h(y,λ)在点(y0,λ0)处进行泰勒展示,首先分别求得

则h(y,λ)的泰勒展示为:

令

则有

对于z(z,u)的解曲线为

由解曲线可知:当u≥0时,z(z,u)存在右极限点(0,0);当u<0时,z(y,u)不存在左极限点.根据障碍点的定义知,(y0,0)是h(y,λ)的前向障碍点.

随后对本部分的相关结论进行数值仿真以验证结论的正确性.

3数值仿真

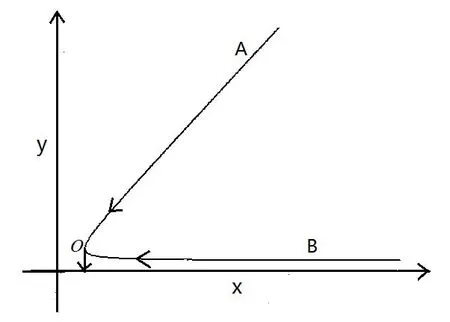
图1　障碍点相平面图

利用上述算法对模型(1)进行数值仿真.不妨取r1=8,k1=10,c=0.6,r=2,b=1,ap=2,d=0.2,得仿真图形1.

图1中折线AOB代表着麦蚜种群对作物种群影响作用,O为模型(1)的障碍点.由图1可以看出麦蚜种群数量在此点骤降为零,这意味着此骤降为有益突变,此时,不需要控制.如果相反过程出现,则为有害突变,此时需要控制消除此突变,这是我们以后要做的工作.

参考文献

[1] 赵慧燕.麦芽防治过程中的尖点突变模型突变区域及防治指标的研究初报[J].系统工程,1991,6:30-35.

[2] Piyaratne M K D K.蚜虫种群动态的燕尾突变区域、参数估计及计算机模拟软件研发与应用[D].咸阳:西北农林科技大学,2013.

[3] Piyaratne M K D K,Zhao Huiyan,Meng Qingxiang.A population dynamics model for wheat aphids based on swallowtail catastrophe theory[J].Ecological Modeling,2013(253):9-16.

[4] Wenqi Wu,M K D K piyaratne,Huiyan Zhao,et al.Butterfly catastrophe model for wheat aphid population dynamics:Construction,analysis and application[J].Ecological Model,2014,288:55-61.

[5] 赵立纯,韩立红,刘敬娜.基于突变现象的麦蚜种群广义生态模型的建立与分析[J].生物数学学报,2016,31(1):101-108.

[6] Leono O Chua.Impasse points Part 1:Numerical aspects[J].International Journal of Circuit Theory and Applications,1989,17:213-234.

(责任编辑：张冬冬)

Catastrophe analysis of singular system models with wheat aphid populations

HAN Lihong1,2,ZHAO Lichun2，LIU Jingna2

(1.College of Mathematics,Liaoning Normal University,Dalian Liaoning 116029,China;2.SchoolofChemistryandLifeScience,AnshanNormalUniversity,AnshanLiaoning114007,China)

AbstractAphid population catastrophe phenomenon has received people’s attention all the time.In the paper,on the basis of the singular system model,the ecology mechanism of breakout of the aphid population is investigated using impasse point analysis.Finally,some simulations are carried out to prove the result.

Key wordswheat aphid populations;catastrophe phenomenon;singular system;impasse point

收稿日期2016-02-20

作者简介韩立红(1989-),女，吉林榆树人，辽宁师范大学数学学院2013级硕士研究生.

中图分类号Q141

文献标识码A文章篇号1008-2441(2016)02-0016-03