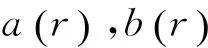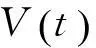具有反馈控制的Schoener模型的渐近周期解

鲁红英,李映夏

(1.东北财经大学 数学学院，辽宁 大连 116025;2.南京信息工程大学 应用气象学院,江苏 南京 210044)



具有反馈控制的Schoener模型的渐近周期解

鲁红英1,李映夏2

(1.东北财经大学 数学学院，辽宁 大连 116025;2.南京信息工程大学 应用气象学院,江苏 南京 210044)

摘要考虑了具有反馈控制的非自治Schoener竞争生态系统.通过建立相应的伴随系统和构造合适的Liapunov函数，得到了该系统唯一存在正的全局渐近稳定的渐近周期解的充分条件.

关键词Schoener模型；反馈控制；Liapunov函数；全局渐近稳定；渐近周期解

1974年，Schoener[1]提出了著名的自治两种群竞争模型：

(1)

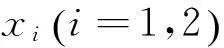
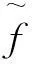
本文考虑如下非自治Schoner竞争模型：

(2)

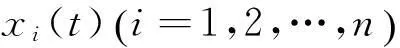
考虑到生态学意义，本文假设系统(2)满足初始条件

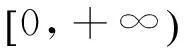
1主要结果

定义2[14]若系统(2)的某个正解

满足：

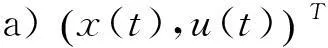
b) 对于系统(2)的任何其它正解

有

称系统(2)是全局渐近稳定的.

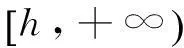
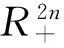
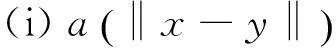
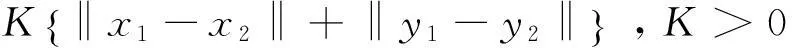
(iii) V′(t,x,y)≤-cV(t,x,y),这里 c>0是一个常数.

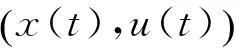
运用文献[17]的研究方法可以得到系统(2)的一致持续生存性，并且给出了系统(2)的最终有界域.

定理1若系统(2)满足

(3)

则系统(2)是一致持续生存的.即集合

是系统(2)的正向不变集和最终有界域，其中,

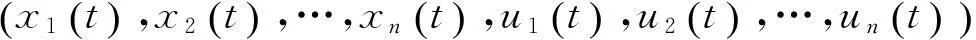
假设xi(t)>Mi，有

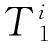
由系统(2)得

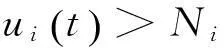
假设xi(t)

假设ui(t)

则系统(2)是一致持续生存的，即集合D是系统(2)的正向不变集且是系统(2)的解的最终有界区域，证毕.

定理2若渐近周期系统(2)满足条件(3)和

(4)

则系统(2)存在唯一正的全局渐近稳定的渐近周期解.

证明根据定理1可知，系统(2)的解是一致最终有界的，且D为一致最终有界区域.为了研究系统(2)渐近周期解的存在唯一性，建立如下伴随系统

(5)

其中，

是系统(2)在D中的任意两个正解，且满足

记

(6)

构造Liapunov函数

设

在初中生物教学中，教师要强化学生对重要概念的理解，使学生主动构建生物知识网络，有助于其生命观念的形成。如围绕光合作用这一重要概念，教师引导学生绘制相应概念图，引导学生对整体知识的理解，帮助学生树立结构和功能、物质和能量等生命观念。在概念教学中，围绕重要概念进行比较分析也是树立生命观念的重要手段，如比较光合作用和呼吸作用的过程、场所和条件既能加深学生理解，也能达到培养生命观念的目的。

又因为

(7)

其中，

由于

所以，

其中，

即

于是

(8)

所以

因而

由式(8)可知，

由引理1，有

故系统(2)是全局渐近稳定的，即系统(2)存在唯一正的全局渐近稳定的渐近周期解.定理2证毕.

2结语

本文研究了具有反馈控制的Schoener模型的动力学行为.通过运用微分比较定理，得出了该系统的一致持续生存性.通过建立相应的伴随系统和构造合适的Liapunov函数，得到了该系统唯一存在正的全局渐近稳定的渐近周期解的充分条件.本文所得的条件是依赖于反馈控制变量的.

参考文献

[1] L Chen,X Song,Z Lu.Mathematical Models and Methods in Ecology[M].Chengdu：Sichuan Science and Technology Press,2003.

[2] L P Wu,F D Chen,Z Li.Permanence and global attractivity of a discrete Schoener’s competition model with delays [J].Mathematical and Computer Modelling,2009,49(7-8):1607-1617.

[3] Q M Liu,R Xu.Periodic solutions of Schoener’s competitive model with delays[J].J Biomath,2004,19(4):385-394 (in Chinese).

[4] H Xiang,K M Yan,B Y Wang.Positive periodic solutions for discrete Schoener’s competitive model[J].J Lanzhou Univ Technol,2005,31(5):125-128.(in Chinese).

[5] W Z Gan,Z G Lin.The asymptotic periodicity in a Schoener’s competitive model[J].Applied Mathematical Modelling,2012,36(3):989-996.

[6] Q M Liu,R Xu，W G Wang.Global asymptotic stability of schoener’s competitive model with time delays[J].J Biomath，2006,21(1):147-152.

[7] T W Zhang,Y K Li,Y Ye.On the existence and stability of a unique almost periodic solution of Schoener’s competition model with pure-delays and impulsive effects[J].Commun Nonlinear Sci Numer Simulat,2012,17(3):1408-1422.

[8] 陈兰荪.数学生态学模型与研究方法[M].北京:科学出版社,1988.

[9] 陆忠华,陈兰荪.周期系数的Schoener 模型分析[J].数学物理学报,1992,12(1):105-109.

[10] 陈超,纪昆.具有连续时滞和不同扩散率的非自治Schoener 模型的概周期解[J].浙江大学学报:理学版，2006,33(5):485-495.

[11] 张利军,霍海峰，陈菊芳.具有反馈控制的Schoener模型的渐近性[J].生物数学学报,2001,16(4):405-410.

[12] 原存德,王春花.非自治具有扩散的Schoener模型的持续生存性与周期解[J].生物数学学报,1997,1(2):17-20.

[13] F Y Wei,K Wang.Global stability and asymptotically periodic solution for non-autonomous cooperation Lotka-Volterra diffusion system[J].Appl Math Comput，2006,182(1):161-65.

[14] 秦元勋,王慕秋,王联.运动稳定性理论与应用[M].北京:科学出版社,1981.

[15] Barbalat I.systems d’equations differentielle d’oscillations nonlinears[J].Rev Roumaine Math Pures Apple，1959,4(2):267-270.

[16] 何崇佑.概周期微分方程[M].北京:高等教育出版社,1992.

[17] 鲁红英.非自治竞争扩散时滞系统的持久性和全局吸引性[J].吉林师范大学学报，2008,29(2):13-15.

(责任编辑：张冬冬)

Asymptotically periodic solution of Schoener model with feedback controls

LU Hongying1,LI Yingxia2

(1.School of Mathematics,Dongbei University of Finance and Economics,Dalian Liaoning 116025,China;2.CollegeofAppliedMeteorology,NanjingUniversityofInformationScienceandTechnology,NanjingJiangsu210044,China)

AbstractA non-autonomous Schoener competition ecosystem with feedback controls is considered in this paper.By establishing a corresponding adjoint system and constructing a suitable Liapunov function,the sufficient conditions are obtained for the existence of an unique positive asymptotically periodic solution which is globally asymptotically stable.

Key wordsSchoener model；feedback control;Liapunov function；globally asymptotic stability;asymptotically periodic solution

收稿日期2016-03-02

基金项目辽宁省普通高等教育本科教学改革研究项目(UPRP20140544)；辽宁省教育厅科学技术研究项目(L2014458)；东北财经大学2015年校级科研项目(DUFE2015Y33).

作者简介鲁红英(1977-),女,辽宁阜新人，东北财经大学数学学院副教授,硕士,从事生物数学及动力系统方向研究.

中图分类号O175.1

文献标识码A文章篇号1008-2441(2016)02-0010-06