具有年龄结构的霍乱传染病模型的最优控制

甘乃峰,谷晓沛

(1.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007;2.鞍山师范学院 教育科学技术学院,辽宁 鞍山 114007)



具有年龄结构的霍乱传染病模型的最优控制

甘乃峰1,谷晓沛2

(1.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007;2.鞍山师范学院 教育科学技术学院,辽宁 鞍山 114007)

摘要建立了具有年龄结构的SIR霍乱传染病模型，基于微分方程给出基本再生数R0的计算方法，利用最优控制理论，对幼年个体施加控制，使染病者个体的数量最小化，并限制染病者和易感染者之间的转化，最后给出数值例子.

关键词年龄结构；传染病模型；最优控制

自从有人类历史记载以来，霍乱作为一种传染疾病已有上千年的历史[1]，尽管当今世界的卫生水平以及医疗水平有了极大的提高，但霍乱这种传染疾病仍然在部分人口密集且医疗水平相对落后地区时有发生，它仍然是目前以及今后一段时间内全世界所面临的一个重要挑战.

霍乱是一种细菌感染的胃肠消化道疾病，表现为腹泻、呕吐不止.人们食用含有超过一定阈值量的弧菌状霍乱病菌食物就会感染此疾病.Harris[2]指出这个阈值不是统一的，并且确定它是比较复杂的问题，但可以肯定的是它与患者年龄是正相关的.疾病形成的时间需要1～5天，一旦一个个体被感染，排泄物就会含有病菌，进一步会感染他人，尤其是那些亲密接触者.

已有学者应用传染病动力学模型对具有年龄结构的传染病进行了系统的研究，取得了一系列的成果.文[3]研究了具有年龄结构的单种群模型在成年种群间传染疾病的问题,建立了成年和幼年两个年龄结构的SI传染病模型,得到模型的唯一正平衡点局部渐近稳定的充分条件.文[4]提出了具有年龄结构的SIS型传染病的接种模型,对模型的动力学性态进行了分析,得到了地方病平衡解唯一存在的条件、平衡解稳定的条件,还研究了接种率的大小对疾病流行的影响.文[5]研究了一类具有年龄结构的SIR型传染病模型,证明了该模型当阈值R0<1时疾病消亡，当阈值R0>1时模型同时具有一致弱持续性质和强持续性质.文[6]针对不同的传染病的传播特点,建立了具有年龄和隔离措施的SEIQR模型、 具有年龄结构的手足口病模型和具有年龄结构和常数迁移率的SIR模型,使用传染病动力学中的有关方法理论对模型进行了分析,得到了模型无病平衡态和地方病平衡态的存在性和稳定性条件.

1模型的建立

图1　两个年龄独立SIR模型的关系描述

(1)

2基本再生数R0的计算

基本再生数R0，指一个病人在平均患病期内所传染的人数.R0的计算，我们采用Van den Driessche and Watmough[7]的方法.

模型(1)的右侧可表示成F-V形式，其中，

其中，F表示两类感染群体中新增加的感染者.

为了简化计算，可取β11=β12，β21=β22，αγS10S20(β11β22-β21β)=0，其中，α=f+e1+g1，γ=e2+g2,模型(1)中的再生数

文献[2]、[8～10]给出了某地区霍乱传染疾病中各参数取值，如表1.

表1　各参数及其量值

经上面的计算方法可得基本再生数R0≈1.54，因为R0>1，由此可断定该地区霍乱将会流行.下面将讨论疾病的最优控制问题.

3最优控制

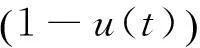
(2)

根据最优控制理论方法，首先选取目标函数为

(3)

我们的目的可以转化为:按照模型(2),在控制集U中选取控制u(t)，使J(u)最小化.下面通过系统的哈密顿函数H，可得到系统最优化和截断函数存在的必要条件.哈密顿函数构造方法如下：

设

因为系统是有界的，从文[11]可知存在最优控制，而且能够求得伴随方程和最优控制的表达式.

截断条件为

最优控制为

该定理的证明与文[12]中证明类似，此处略.

4数值模拟

为了探寻最优控制中各种权重参数的影响，A,B,C可取各种量值情况，控制变量取值范围从0.1～0.9，按照上面的方法，每次得到的控制变量的最大值的结果相似，因此不妨取A=1,B=1,C=10，其它参数值参见表1，通过最优控制方法计算可得，施加控制后，该地区每年霍乱都会爆发，但会迅速下降，感染个体的最大数量不会超过150人.

5结论

本文建立幼年个体和成年个体分别独立的SIR霍乱传染病模型，应用文[7]中的方法，给出基本再生数R0的计算，用来确定传染疾病是否能够传播.若疾病传播，则对幼年个体施加控制，建立一个控制模型.利用最优控制理论，使染病者和易感者的数量最小化，移出者的数量最大化.

参考文献

[1] Dhiman Barua,Willliam B,Greenough III.Current Topics in Infectious Disease:Cholera[M].New York:Plenum publishing Corporation,1992.

[2] Jason B Harris,Regina C LaRorocque,Fahima Chowdhury，et al.Susceptibility to Vibrio cholerae Infection in a Cohort of Household Contacts of Patients with Cholera in Bangladesh[J].Plos Neglected Tropical Diseases,2008,2(4):3-4.

[3] 张剑,张宏民.具有年龄结构的SI传染病模型的分析[J].东北农业大学学报,2010,41(8):131-134.

[4] 刘汉武，徐洁，刘启明.连续接种的具有年龄结构的SIS型传染病模型[J].工程数学学报,2002,19(4):25-29.

[5] 陈庚.一类具有年龄结构的传染病模型的持续性质[J].高校应用数学学报(A辑),2007,22(3):253-262.

[6] 苏细容.具有年龄结构的传染病模型研究[D].北京：北京林业大学,2010.

[7] P van den Driessche,James Watmough.Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J].Mathematical Biosciences,2002,180(1-2):29-48.

[8] Wolfam Alpha[EB/OL].http://www.worlframalpha.com/input/?i=bangladesh+births,2010-07-28.

[9] Eric J Nelson,Jason B Harris,J Glenn Morris Jr,et al.Cholera transmission:the host,pathogen and bacteriophage dynamic[J].Journal Reviews Microbiology,2009,7:693-702.

[10] World Health Organization[EB/OL].http://www.who.int/mediacentre/factsheets/fs107/en/index.htm, 2010-05-12.

[11] Wendell H Fleming,Raymond W Rishel.Deterministic and Stochastic Optimal Control[M].Berlin:Springer,1975.

[12] Suzanne lenhart,John T Workman.Optimal Control Applied to Biological Models[M].London:Chapman and Hall/CRC,2007.

(责任编辑：张冬冬)

Optimal control of an epidemic cholera model with age class structure

GAN Naifeng1，GU Xiaopei2

(1.School of Mathematics and Information Science,Anshan Normal University,Anshan Liaoning 114007,China;2.SchoolofEducationalScienceandTechnology,AnshanNormalUniversity,AnshanLiaoning114007,China)

AbstractIn this paper,an epidemic cholera model with age class structure is given.Using the system of ordinary differential equations,the general formula for R0is calculated.We use the optimal control strategies to minimize the susceptible and infected individuals and to maximize the number of recovered individuals,the interactions between susceptibles and infecteds are limited.Finally,the results of numerical results is given.

Key wordsage structure;epidemic model;optimal Control

收稿日期2016-02-20

作者简介甘乃峰(1974-)，男，辽宁沈阳人，鞍山师范学院数学与信息科学学院讲师，博士.研究方向：鲁棒控制、算子理论.

中图分类号O232

文献标识码A文章篇号1008-2441(2016)02-0004-06