Banach空间上和矩阵Drazin逆的两种表示

林梅羽

(莆田学院 基础教育学院，福建 莆田 351100)



Banach空间上和矩阵Drazin逆的两种表示

林梅羽

(莆田学院 基础教育学院，福建 莆田 351100)

摘要矩阵的Drazin逆在奇异微分方程、密码学、数值分析以及特征值问题中的扰动界等方面都有着重要的应用.给出在条件A3B=0,A2B+BAB=0，以及ABAB=0下和矩阵(A+B)的Drazin逆的两种对称表达形式，并通过数值例子解释了该表达形式.

关键词Banach空间；Drazin逆；和矩阵

设Cm×n是复数域上m行n列的复矩阵集.

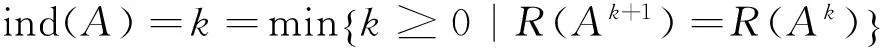
(1)Ak+1B=Ak；

(2)BAB=A；

(3)AB=BA.

则称矩阵B为A的Drazin逆，记作AD[1].

当k=0时，A的Drazin逆AD即为方阵可逆的广义逆A-1；当k=1时，A的Drazin逆AD即为矩阵A群逆A#.

为了叙述的方便，引入Aπ=I-AAD和A0=I，其中I为对应的单位矩阵.

矩阵的Drazin逆在奇异微分方程、差分方程、Markov链、迭代方法、密码学、数值分析以及结构化矩阵在相对特征值问题中的扰动界等众多问题中都有着重要的应用[1].

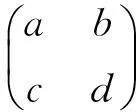
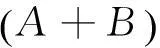
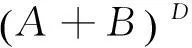
1和矩阵的Drazin逆

引理1[1]设A∈Cm×n，B∈Cm×n,则

引理2[5]设A∈Cm×n，B∈Cm×n,如果AB=0，则

其中,t=max{ind(A),ind(B)}.

引理3[8]设

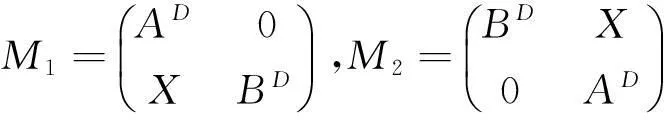
定理1设A∈Cm×n，B∈Cm×n.如果A3B=0,A2B+BAB=0,ABAB=0,则

A2BXAD+A2BDXA+AB2XAD+ABBDXA+BABXAD+BABDXA,

其中,

t=max{ind(A2),ind(B2)}.

令

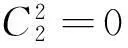
t=max{ind(A2),ind(B2)}.

则

其中，

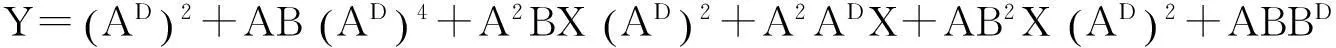
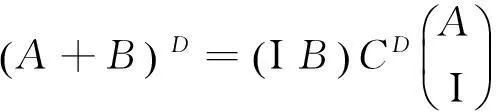
类似地，由矩阵A和B的对称性可以给出上述定理1的对称形式.

定理2设A∈Cm×n，B∈Cm×n.如果AB3=0,AB2+ABA=0,BABA=0,则

B2AXBD+B2ADXB+BA2XBD+BAADXB+ABAXBD+ABADXB，

其中，

t=max{ind(A2),ind(B2)}.

2数值例子

选取两个数值例子来验证.

设矩阵A∈C3×3，B∈C3×3，取特殊矩阵如下所示：

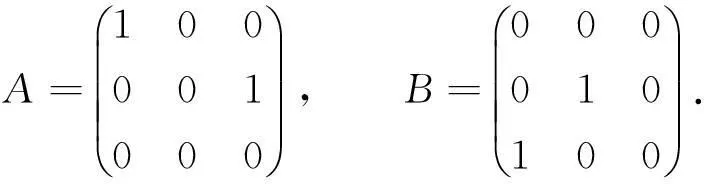
通过矩阵计算，显然易知

A3B=0,A2B+BAB=0,ABAB=0.

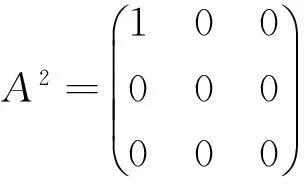
则由定理1可得

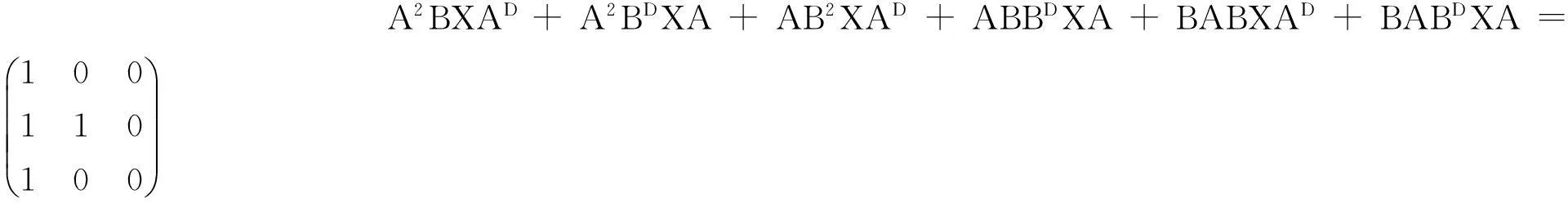
同理，类似地可以验证定理2.

参考文献

[1] A Ben-Isracel,T N E Greville.Generalized Inverses:Theory andApplications[M].New York:Springer,2003.

[2] J Miao.Results of Drazin inverse of a 2X2block matrices[J].J Shanghai Normal University,1989,18:25-31.

[3] 董鹏飞.Schur补为零的分块矩阵Drazin逆表示[D].哈尔滨：哈尔滨工程大学，2011.

[4] 郭美华,刘丁酉.分块2次幂零矩阵的广义Schur补[J].武汉大学学报，2015,31(3):633-637.

[5] R E Hartwig,G Wang,Y Wei.Some additive results on Drazin inverse[J].Linear Algebra and Its Applications,2001,322(1-3):207-217.

[6] N Castro Gonzalez.Additive perturbation results for the Drazin inverse[J].Linear Algebra and Its Applications,2005,397:279-297.

[7] H Yang,X F Liu.The Drazin inverse of the sum of twomatrices and its applications[J].Journal of Computational andApplied Mathematics,2011,235(5):1412-1417.

[8] C D Meyer Jr,N J Rose.The index and the Drazin inverse of block triangular matrices [J].SIAM Journal on AppliedMathematics,1977,33(1):1-7.

(责任编辑：张冬冬)

Some expressions of the Drazin inverse of the sum of two matrices in Banach space

LIN Meiyu

(School of Basic Education,Putian University,Putian Fujian 351100,China)

AbstractThere are important applications of the Drazin inverse in singular differential equations,cryptography,numerical analysis and perturbation bounds for the eigenvalue problems.It gives two symmetric expressions ofDunder the conditions of A3B=0,A2B+BAB=0,ABAB=0,and it gives the numerical example to illustrate the expression.

Key wordsBanach space;Drazin inverse;Sum matrices

收稿日期2016-01-12

作者简介林梅羽(1959-)，男，福建莆田人，莆田学院基础教育学院高级讲师.

中图分类号O153.3

文献标识码A文章篇号1008-2441(2016)02-0001-03