波形钢腹板箱梁的临界屈曲应力分析
2016-07-13曹雪峰
曹雪峰
(衡阳公路桥梁建设有限公司, 湖南 衡阳 421001)
波形钢腹板箱梁的临界屈曲应力分析
曹雪峰
(衡阳公路桥梁建设有限公司, 湖南 衡阳421001)
摘要:通过对波形钢腹板箱梁的临界屈曲应力进行有限元数值模拟,结合相应屈曲理论计算其临界屈曲应力,对比分析了计算得出的各种临界屈曲应力,同时将波形钢腹板的波高、直板段水平长度、水平折叠角、腹板高度与厚度的尺寸改变,分析对其箱梁临界屈曲应力特性的影响规律。分析表明: ①波形钢腹板的波高的变化基本不会对箱梁的临界屈曲应力造成影响; ②避免波形钢腹板结构的局部屈曲失稳,直板段水平长度不宜过长; ③波形钢腹板的水平折叠角的增大可有效的提高整体屈曲的稳定性; ④设置的腹板高度不宜过高,以防止整体屈曲失稳; ⑤适当增加腹板的厚度有利于结构局部屈曲稳定性提高。
关键词:波形钢腹板; 箱梁; 临界屈曲应力; 有限元分析
0引言
结构自重是影响桥梁安全性的主要原因之一。与普通混凝土腹板箱梁桥相比,波形钢腹板箱梁桥是以1 mm左右的钢板替代40~80 cm厚的混凝土腹板,相应结构自重降低,跨越能力增强,因此,波形钢腹板不仅能节约成本,而且能提高施工的效率[1]。一般箱梁桥主梁的全部剪切应力主要作用在波形钢腹板上,其各应力的大小基本相同[2]。由于波形钢腹板的抗剪强度、剪切屈曲强度是确定其结构尺寸的主要因素,其中腹板上承受的极限剪力小于使用钢材的剪切强度即满足抗剪强度的要求,而剪切屈曲强度则需钢腹板同时符合局部屈曲、合成屈曲、整体屈曲等相关条件[3-5]。
本文以一座独塔无背索波形钢腹板箱梁部分斜拉桥采用的波形钢腹板为例,对主跨部分波形钢腹板箱梁的临界屈曲应力进行有限元数值模拟,通过结合相应屈曲理论计算其临界屈曲应力,并对比分析了计算得出的各种临界屈曲应力。同时,将波形钢腹板的波高、直板段水平长度、水平折叠角、腹板高度与厚度的结构尺寸改变,分析各参数对其箱梁临界屈曲应力特性的影响规律。研究结果可为今后同类工程的设计与施工提供理论依据。
1工程概况
项目的大桥梁体全长228 m,桥宽50 m,三跨(30+70+30)m波形钢腹板箱梁桥。梁体采用波形钢腹板预应力混凝土组合箱梁结构,其中箱梁的上顶板、下底板均使用C50混凝土进行浇筑。波形钢腹板采用Q345qC型钢材,单周期内的水平长度l=1.2 m,其中两段直板a与两段斜板c的水平长度分别为0.33、0.27 m,水平折叠角β为36.5°,腹板高度H为1.5 m,波高h为0.2 m,腹板厚t为0.12 m,材料与结构尺寸参数如表1、图1所示。
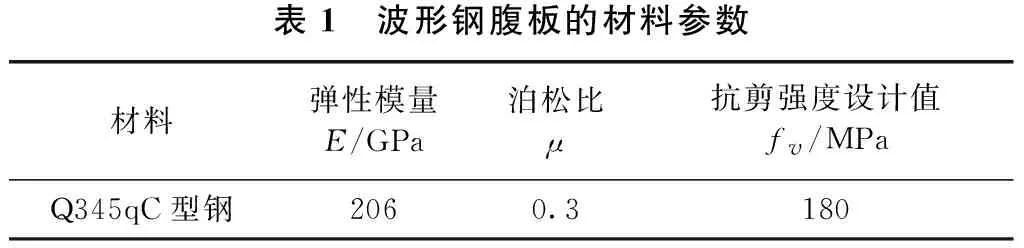
表1 波形钢腹板的材料参数材料弹性模量E/GPa泊松比μ抗剪强度设计值fv/MPaQ345qC型钢2060.3180
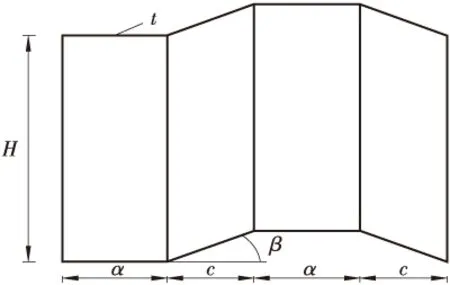
图1 波形钢腹板的结构参数几何尺寸
2相关屈曲理论
因波形钢腹板的厚度一般比较薄,在实际工程中需特别注意其屈曲应力问题。整体屈曲、合成屈曲和局部屈曲是波形钢腹板箱梁屈曲表现的3种常见形式[6]。由经典弹性理论可知,当波形钢钢腹板的水平折叠角β较小时,箱梁的临界屈曲应力表现为整体屈曲;而水平折叠角β较大时,箱梁的临界屈曲应力表现为局部屈曲[7]。
根据S.P.Timoshenko公式,钢腹板内任意直板段的两折点之间所承受的局部屈曲应力可以表示为[8]:
(1)
式中:k为局部屈曲系数,依据四边简支取值5.35;E为钢材弹性模量;μ为钢材泊松比;t为钢腹板的厚度;a为直板段水平长度。
依据伊斯利公式,波形钢腹板所承受的整体屈曲应力可以描述为[9]:
(2)
式中:k为整体屈曲系数,依据四边简支取值31.6;E为钢材弹性模量;t为钢腹板的厚度;a为直板段水平长度;β为水平折叠角;hw为腹板高度。
根据国外相关专家对波形钢腹板箱梁的局部屈曲剪切应力τcr,l、合成屈曲剪切应力τcr,i以及整体屈曲剪切应力τcr,g的实验与研究,其3种应力形式之间关系可以表达为[10]:
(3)
通过式(1)~式(3)可知:在相同材料与边界条件的情况下,波形钢腹板的直板段水平长度a与厚度t是决定其局部屈曲剪切应力τcr,l的主要因素;而整体屈曲剪切应力τcr,g在局部屈曲剪切应力τcr,l基础上还受到波形钢腹板高度hw与水平折叠角β因素的影响;其τcr,i<τcr,l<τcr,g,因此,将波形钢腹板的合成屈曲剪切应力τcr,i作为钢腹板结构设计的控制应力基本没有问题。然而,通过屈曲相关理论公式计算得出的剪切应力与实际工程钢腹板结构发生的屈曲剪切应力相比较大,同时为确保结构的正常运营,防止偶然突增荷载导致结构损坏,需将合成屈曲应力τcr,i除以一个安全因数n(n可取值为1.5)作为波形钢腹板结构的控制屈曲剪切应力τcr,则其控制屈曲应力τcr可描述为:
(4)
将该桥梁波形钢腹板采用Q345qC型钢材的弹性模量E与泊松比μ参数值分别导入式(1)、式(2),则结构的局部屈曲剪切应力计算公式可简化成式(5),整体屈曲剪切应力计算公式可简化成式(6)。
(5)
(6)
3有限元数值模拟
为研究波形钢腹板箱梁临界屈曲应力的变化规律,将该桥梁主跨部分的箱梁建成一个简化空间有限元模型进行数值模拟,其中X、Y、Z分别表示箱梁的长度(纵向)、高度(竖向)、宽度(横向),且中间不设横隔板。由于波形钢腹板箱梁上顶板与下底板的混凝土厚度不会引起其抗剪、屈曲应力发生变化,因此本次试验采用等厚度的上下板箱梁,从而减少与试验无关的数据计算,有利于有限元网格的划分。波形钢腹板与箱梁均按实际桥梁所用的规格设置有限元空间模型,采用实体单元Solid65、Solid85分别对混凝土底顶板和波形钢腹板进行模拟,整个模型共设立159 976个线性单元,节点56 370个。其有限元空间模型如图2~图4所示。

图2 波形钢腹板箱梁有限元空间模型整体

图3 波形钢腹板箱梁有限元空间模型局部

图4 波形钢腹板有限元空间模型
在实际工程中箱梁结构在正常情况下不允许发生屈服现象,因此,本次试验主要对箱梁结构的特征值屈曲变化规律(线性屈曲)进行计算分析。在屈曲的数值分析中,由于箱梁结构所承受均布线荷载的特征值等于实际临界屈曲荷载,则其承载应力的大小即可表示为箱梁结构所承受的临界屈曲应力。选取屈曲模态中第1阶段特征值作为计算结果,同时为保证计算的准确性,本次试验采用子空间迭代法进行计算[11]。在有限元空间模型中,箱梁结构的两端为简支,并对箱梁的跨中输入均布线荷载,确保整个箱梁结构中各个截面所承受的剪力相同,便于确定波形钢腹板箱梁临界屈曲应力的大小[12]。
4结果与分析
4.1标准有限元模型的临界屈曲应力
采用有限元软件对波形钢腹板箱梁结构的临界屈曲应力进行数值模拟,同时结合相关理论公式分别对箱梁结构的局部屈曲应力τcr,l、合成屈曲应力τcr,i、控制屈曲应力τcr、整体屈曲应力τcr,g进行计算。其计算结果如表2所示。

表2 临界屈曲应力理论计算结果MPa有限元值局部屈曲应力τcr,l整体屈曲应力τcr,g合成屈曲应力τcr,i控制屈曲应力τcr7201319.84067.5996.6666.7
根据表2可知:通过有限元数值模拟所得的临界屈曲应力和结合理论公式计算所得的控制屈曲应力大小即为相近,同时两者的临界屈曲应力均比钢材抗剪强度设计值fv较大,说明箱梁结构的安全性能由fv决定。在合理的承载下不会引起波形钢腹板箱梁结构发生屈曲失稳,即其结构设计合理。
4.2波高对临界屈曲应力的影响
分别以波高h=0.1、0.15、0.2、0.25、0.3 m为例,研究不同波高对波形钢腹板箱梁临界屈曲应力的影响,其中h=0.2 m为实际尺寸。由于水平折叠角β保持不变,当改变波形钢腹板波高h必然会引起斜板段水平长度c发生相应改变,而其余尺寸均按波形钢腹板实际所用的规格进行计算。计算所得结果如表3所示。
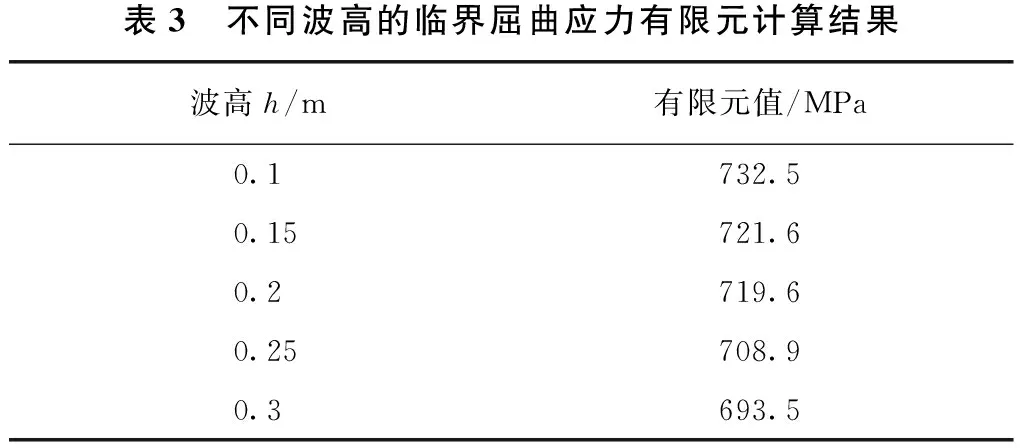
表3 不同波高的临界屈曲应力有限元计算结果波高h/m有限元值/MPa0.1732.50.15721.60.2719.60.25708.90.3693.5
根据有限元计算结果表3可知:波形钢腹板的波高h与箱梁结构所承受的临界屈曲应力呈相反变化关系,且变化的程度较小,可忽略不计;而基于上述理论公式计算得出箱梁结构的临界屈曲应力与波形钢腹板的波高h无关。由此可知,波高h的变化不会对箱梁结构造成影响。此外,由有限元计算结果可知:钢材抗剪强度设计值fv比波形钢腹板不同波高h的临界屈曲应力有限元计算值较小,因此实际上对箱梁结构作用的仍为fv。而且当增大波形钢腹板波高h必然会引起斜板段水平长度c也相应增大,造成不必要的材料浪费。
4.3直板段长度对临界屈曲应力的影响
通过以直板段水平长度a=0.33、0.39、0.45、0.51、0.57、0.63、0.69 m为例,研究不同直板段水平长度对波形钢腹板箱梁临界屈曲应力的影响,其中a=0.33 m为实际工程尺寸。其余参数均按实际尺寸,分别采用相关理论公式计算和有限元空间数值模拟得出相应波形钢腹板箱梁结构的临界屈曲应力值。其变化规律如图5所示。
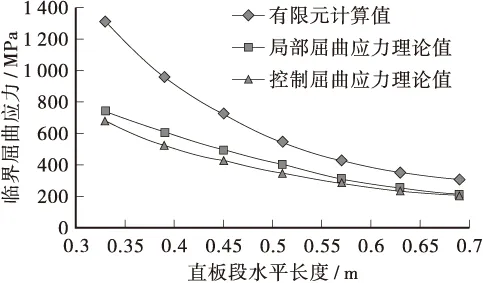
图5 不同直板段长度a的临界屈曲应力变化规律
根据图5可知:通过有限元空间数值模拟得出不同直板段水平长度a的临界屈曲应力均大于相关理论公式计算值,且均与箱梁结构所承受的临界屈曲应力呈相反变化关系。且根据公式(6)可知:当箱梁结构的整体屈曲应力理论值达到极限时,不会对其结构整体屈曲稳定性造成影响。在直板段长度a=0.69 m时,箱梁结构的控制屈曲应力理论值基本与fv相等,说明此时箱梁结构的稳定性接近极限。此外,由有限元数值模拟得出的结果与控制屈曲应力理论值相差较小,表明试验结果较为合理。综上所述,为确保实际工程中箱梁结构的安全与材料利用率,波形钢腹板的水平段长度不应大于0.7 m,其范围控制在0.3~0.55 m最佳。
4.4腹板高厚比对临界屈曲应力的影响
由经典力学理论可知:波形钢腹板的高厚比越大,相应箱梁结构的屈曲更易失稳破坏。高厚比H/t的改变方式主要为波形钢腹板厚度t的改变和高度H的改变。因此,本次试验以改变钢腹板t、H的方式,分别对不同高厚比条件下箱梁结构临界屈曲应力的变化规律进行研究,其余参数均为实际尺寸,并采用相关理论公式计算和有限元空间数值模拟得出相应波形钢腹板箱梁结构的临界屈曲应力值。其变化规律如图6、图7所示。
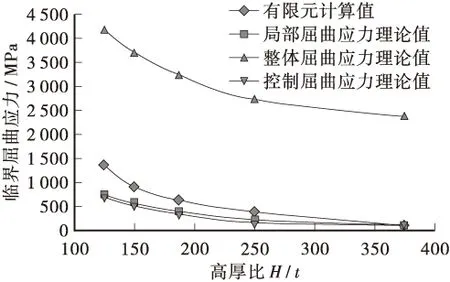
图6 H=1.5 m时临界屈曲应力H/t的变化规律
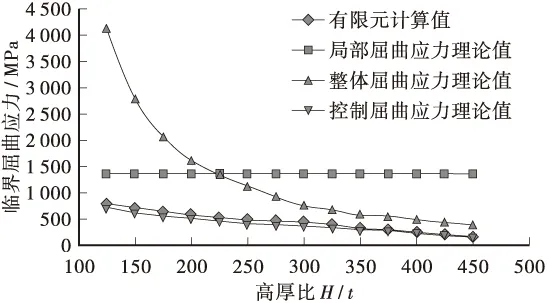
图7 t=12 mm时临界屈曲应力H/t的变化规律
根据图6可知:将波形钢腹板的高度H=1.5 m(实际尺寸)保持不变,减小t致使高厚比增大。当增大波形钢腹板的高厚比,其所受的各临界屈曲应力均逐渐减小,其中整体屈曲应力较大,不会对箱梁结构整体屈曲的稳定造成影响。在高厚比H/t=375时,箱梁结构的控制屈曲应力已经小于100 MPa,说明此时的控制屈曲应力远小于钢材抗剪设计值fv,即屈曲应力的大小决定箱梁结构的稳定与安全。此外,由有限元数值模拟得出的结果与控制屈曲应力理论值相差较小,表明试验结果较为合理。综上所述,为确保实际工程中箱梁结构的安全储备,同时避免材料的浪费,波形钢腹板的厚度不应小于6 mm,其范围控制在8~12 mm最佳。
根据图7可知:将波形钢腹板的厚度t=12 mm(实际尺寸)保持不变,增大H致使高厚比增大。当增大波形钢腹板的高厚比,其局部所受屈曲应力保持相对较大的理论值不变,说明此时箱梁结构局部稳定性较好,无局部屈曲破坏失稳的可能。整体屈曲应力降低幅度较大,从而引起钢腹板控制屈曲应力相应降低。在H/t=450时,波形钢腹板箱梁结构的控制屈曲应力已完全小于fv,说明此时屈曲应力对箱梁结构稳定起决定作用。此外,由有限元数值模拟得出的结果与控制屈曲应力理论值相差较小,表明试验结果较为合理。综上所述,为确保实际工程中箱梁结构的安全与材料利用率,钢腹板的高度不应大于5 m。
4.5水平折叠角对临界屈曲应力的影响
大量研究表明,波形钢腹板的设计高度控制在1.5~2.5 m范围内最为合理。分别以波形钢腹板高度H=1.5 m(实际尺寸)、2 m、2.5 m为例,对水平折叠角β=35°、30°、25°、20°、15°、10°、5°(实际尺寸)的箱梁结构临界屈曲应力进行数值分析。由于水平折叠角β的改变,必然会引起钢腹板的斜板段水平长度c、波高h的相应改变。其余参数均为实际尺寸。其变化规律如图8~图10所示。

图8 H=1.5 m临界屈曲应力随水平折叠角的变化规律

图9 H=2 m临界屈曲应力随水平折叠角的变化规律
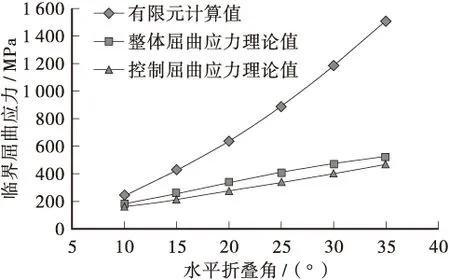
图10 H=2.5 m临界屈曲应力随水平折叠角的变化规律
根据图8可知:在波形钢腹板高度H=1.5 m时,箱梁结构的整体屈曲应力随着水平折叠角β的减小逐渐降低,同时引起结构的控制屈曲应力相应降低。且由公式(5)可知:箱梁结构的局部屈曲应力较大,同时与水平折叠角β无关,箱梁结构无局部屈曲失稳的可能。在水平折叠角β=5°时,波形钢腹板箱梁结构的控制屈曲应力已完全小于fv,说明此时屈曲应力对箱梁结构稳定起决定作用。此外,由有限元数值模拟得出的结果与控制屈曲应力理论值相差较小,表明试验结果较为合理。综上所述,为避免实际工程中发生屈曲破坏失稳,同时保证箱梁结构具备较大安全储能,其水平折叠角β不宜设计过小。
根据图9、图10可知:在波形钢腹箱梁结构发生屈曲破坏失稳时,其腹板高度H越大,相应水平折叠角β越大。因此,设计合理的波形钢腹板需对腹板高度H与水平折叠角β进行综合考虑。此外,图9与图10反映的临界屈曲应力变化规律相似图8,以下不做赘述。
5结论
1) 波形钢腹板的波高的变化基本不会对箱梁的临界屈曲应力造成影响。
2) 波形钢腹板的直板段水平长度不宜过长,以避免波形钢腹板结构的局部屈曲失稳。
3) 波形钢腹板的水平折叠角的增大可有效的提高整体屈曲的稳定性,从而有效的避免整体屈曲失稳。
4) 设置的腹板高度不宜过高,以防止整体屈曲失稳。
5) 适当增加腹板的厚度,有利于结构局部屈曲稳定性提高。
参考文献:
[1] 杨明,黄侨,马文刚,等.波纹钢腹板体外预应力箱梁混凝土块式转向装置力学性能研究[J].工程力学,2012,29(2):185-191.
[2] 马磊,周林云,万水.单箱三室波形钢腹板箱梁剪力滞效应研究[J].中外公路,2013,33(3):95-99.
[3] Jung K,Kim K,Sim C,et al.Verification of incremental launching construction safety for the ilsun bridge,the world’s longest and widest prestressed concretebox girder with corrugated steel web section[J].Journal of Bridge Enginecring,2011,16(3):453-460.
[4] Shao X,Wang H,Ghao H,et al.Experimental study on multicantilever prestressed composite beams with corrugated steel webs[J].Journal of Structural Enginccring,2010,136(9):1098-1110.
[5] 万水,李淑琴,马磊.波形钢腹板预应力混凝上组合箱梁结构在中国桥梁工程中的应用[J].建筑科学与工程学报,2009,26(2):15-20.
[6] 《中国公路学报》编辑部.中国桥梁工程学术研究综述·2014[J].中国公路学报,2014,27(5):1-96.
[7] Liu X G,Fan J S,Nie J G,et al.Behavior of composite rigid frame bridge under bi-directional seismic excitations[J].Journal of Traffic and Transportation Engineering(English Edition),2014,1(1):62-71.
[8] 徐岳,朱万勇,杨岳.波形钢腹板PC组合箱梁桥抗弯承载力计算[J].长安大学学报(自然科学版),2005,25(2):60-64.
[9] 王圣保.偏心荷载作用下波形钢腹板PC组合梁的力学特性[J].中国公路学报,2012,25(6):68-73.
[10] 李立峰,彭酮,土文.波形钢腹板组合箱梁剪力滞效应的理论与试验研究[J].公路交通科技,2009,26(4):78-83.
[11] 周茂定,刘世忠,杨子江.波形钢腹板组合箱梁剪力滞效应的比拟杆法求解[J].兰州交通大学学报,2012,31(4):41-44.
[12] 吴文清,叶见曙,万水,等.波形钢腹板混凝上组合箱梁截面变形的拟平截面假定及其应用研究[J].工程力学,2005,22(5):177-180,198.
文章编号:1008-844X(2016)02-0132-05
收稿日期:2016-04-13
作者简介:曹雪峰( 1978-) ,男,工程师,主要从事路桥建设。
中图分类号:U 448.21+3
文献标识码:A
