基于ARIMA的PPI时间序列分析

耿　强



基于ARIMA的PPI时间序列分析

耿强

摘要：ARIMA模型是一类精度较高的时间序列短期预测模型，本文借助于计量经济学软件Eviews对我国2010年5月到2012年7 月PPI时间序列数据建立了ARIMA（0，1，1）模型，并对未来我国PPI的走势进行了预测分析。

关键词：ARIMA模型；PPI；CPI；时间序列分析

一、PPI

PPI即生产者物价指数，也称作工业品出厂价格指数，是统计部门收集整理的多个物价指数中的其中一个，通常用来衡量制造商出厂价的平均变化的指数，对于市场的敏感度很高。当生产物价指数比预期数值要高时，说明会有通货膨胀的风险。当生产物价指数比预期数值低的时候，则说明有通货紧缩的风险。PPI主要目的是衡量商品在不同生产阶段价格的变化情况。通常情况下，商品的生产可以分成三个阶段：一是原始阶段：商品没有做任何的加工；二是中间阶段：商品需要作进一步的加工；三是完成阶段：商品不再有任何的加工手续。 PPI之所以重要，是因为PPI是反映某一时期生产领域的价格变动情况的重要经济指标，是衡量企业产品出厂价格变动程度和变动趋势的指数，并对制定国民经济核算和相关经济政策有重要影响。当前，我国PPI的调查产品大概有4000多种（含规格品9500多种），覆盖了39个工业行业，涉及的调查种类有186个。

PPI不仅是一个指数，还是一族指数，代表生产中三个渐进过程的每一个阶段的价格指数：原材料、中间品和产成品。对金融市场最有影响的就是产成品的PPI。它代表着这些商品被运到批发商和零售商之前的最终状态。

PPI的计算法则：计算代表规格品的价格指数采用几何平均法，计算代表产品的价格指数采用简单算术平均法，计算工业品出厂价格总指数则采用加权算术平均法。

二、CPI与PPI

CPI表示消费者物价指数，它是用来反映居民家庭购买消费商品及服务的价格水平的变动情况，通常作为衡量通货膨胀的重要指标。

根据价格传导规律，PPI对CPI也有一定的影响。CPI反映消费环节的价格水平，PPI反映生产环节的价格水平。整体价格的波动首先出现在生产领域，然后通过产业链向下游产业扩散，最后会涉及消费品。产业链可以分为下面两条：一是以工业品为原材料的生产，即原材料→生产资料→生活资料的传导；二是以农产品为原料的生产，即农业生产资料→农产品→食品的传导。

**.Correlation is significant at the 0.01 level（2-tailed）.

以上从定性的角度说明CPI与PPI的关系，为了检验以上的结论，本文从定量的角度对数据进行分析。选取2008年1月——2012年7月的CPI和PPI数据进行比对。显示CPI与PPI波动的状况一致，而且对两个独立样本做非参数与参数检验时的p值非常小，说明两种存在相关关系。相关系数也相对较大，说明PPI与CPI的相关性也很强。

PPI与CPI作为宏观经济的两个重要指标，通常可以根据两者的走势了解宏观经济状况。当CPI不断上涨，而PPI仍然处于企稳或者下跌的时候，经济就开始步入繁荣期，因为总需求不断扩张的同时，供给相对充足，此时企业利润将不断向上攀升；当CPI开始向下走，而PPI却不断向上攀升，此时，经济就开始步入衰退期，因为CPI的下降表示总需求开始收缩，而PPI的攀升则显示经济规模的扩大已经受到上游行业或者资源的约束。

三、基于PPI定性分析

2011年7月，我国的PPI同比增幅一直处于下降趋势，我们从以下两方面分析：

一是国外大宗商品价格下降；二是国内通货膨胀趋于缓和。

2010年开始，我国为了克服通胀，央行持续上调存款准备金，中国经济处于收缩状态。并且国内经济产能出现了严重过剩状况，比如钢铁行业。以前中国的重化工业既有海外外需市场的推动，又有国内固定资产投资高速增长的拉动，这样巨大的需求可以说满足了中国工业产品供应。随着金融危机和欧美主权债务危机对中国外需的压制，中国对房地产进行了宏观调控，固定资产增速大幅下滑，最终通过PPI的下降和工业增速下降体现出来了。目前来看，短时间内还很难出现改变。

四、建立ARIMA模型

1.数据选取

2010年5月开始，PPI同比增幅呈现下降趋势。由于采用同比的计算方式，可以忽视季节性的影响因素。

2.对非平稳序列进行平稳化处理

对于非平稳序列，选择差分法来对确定信息进行提取，是一种非常方便有效的方法。通常差分法的选择，有以下规律：（1）序列呈现显著的线性趋势，通常我们使用一阶差分；（2）序列呈现曲线趋势，则使用低阶（二阶、三阶）差分就能提取出曲线的趋势；（3）呈现固定周期时，进行步长为周期长度的差分运算。

观察PPI从2010年5月到2012年7月的时间序列值，可以发现呈现线性趋势。为了得到平稳的时序，我们对原数据采用一阶差分法。差分后的数据dif（x），大致围绕0.5上下波动，可以大致判断该时序趋于平稳。继而再观察dif（x）的自相关系数，自相关系数ρ快速衰减向0。由于平稳时序通常具有短期相关性，因此随着延迟期数k的增加，平稳序列自相关系数会快速衰减到0，由此可以认为一阶差分后的时序是平稳的。

3.纯随机性检验（a=0.05）

如果各序列值之间不存在任何的相关性，那就表明该序列是一个无记忆的序列，过去的行为对未来的走势没有任何影响，这种序列称为纯随机性序列。序列的纯随机性检验，我们可以采用假设检验的方法。由于序列的相关性具有偶然性，则原假设：延迟期数小于或等于m期的序列值，且相互独立，即如下表述：

（1）假设条件

H0:p1=p2=…pm=0，m≥1；

H1：至少存在某个pk≠0，m≥1，k≤m

（2）检验统计量LB

根据LB统计量，它服从自由度为m的卡方分布（m为指定延迟阶数）。

检验结果显示，在6阶延迟下LB统计量的 p值为0.0076，远小于a（a=0.05）。又因为平稳序列通常具有短期相关性，所以有很大把握拒绝原假设，此序列为非白噪声序列。

4.拟合ARIMA（p，d，q）模型

模型根据平稳时间序列的自相关阶数 p和移动平均阶数q的截尾性和拖尾性，选择适当的值来进行拟合。根据样本自相关图显示，除了延迟一阶的自相关系数在2倍的标准差范围之外，其他阶数的自相关系数都在2倍标准差之内波动，可以认为该序列自相关系数一阶截尾，可以用ARIMA（0，1，1）拟合模型。根据样本的偏自相关图显示，除了延迟一阶的偏自相关系数在2倍标准差范围之外，其他阶数的自相关系数都在2倍标准差之内波动，可以认为该序列自相关系数一阶截尾，可以用ARIMA（1，1，0）拟合模型。综合样本的自相关图与偏自相关图，也可以选择ARIMA（1，1，1）。

5.参数估计与模型检验

对拟合好的模型进行参数估计，通常有三种方法（矩估计、极大似然估计、最小二乘估计），这里采用最小二乘估计法。在ARMA（p，q）模型场合下，计算残差平方和达到最小的那组参数是模型参数估计值。再对估计的参数进行显著性检验，检验参数所对应的自变量对因变量的影响是否明显。

（1）若p=1，拟合ARIMA（1，1，0）

参数的估计值Φ1=0.74260，检验未知参数显著性的t检验统计量p 〈0.0001，说明该参数显著非零。

（2）若q=1，拟合ARIMA（0，1，1）

参数的估计值θ1=0.75855，检验未知参数显著性的t检验统计量p 〈0.0001，说明该参数显著非零。

（3）若p=1，q=1，拟合ARIMA（1，1，1）

参数的估计值Φ1=0.61954，θ1=-0.27081，θ1的检验0.3091明显大于0.05，所以参数检验不显著，模型需舍弃。

6.模型的显著性检验

如果模型拟合的残差项中不再含有任何相关信息，即残差序列为白噪声序列，这样的模型称为显著有效模型。与此同时，构建LB统计量，原假设残差序列为白噪声序列，然后对LB统计量进行白噪声检验。从检验的结果能够得到模型LB统计量的p值均明显大于0.05，所以两个模型均显著有效。

7.模型的最优选择

模型的选择是预测工作的重要环节，实证研究表明，同一个序列不仅仅只能构造一个拟合模型，那么选择哪个模型用于统计推断呢？

为了解决这个问题，需引进SBC和AIC信息准则的概念。AIC认为一个拟合模型的好坏可从以下两方面去考虑：一方面是拟合程度的似然函数值，另一方面是模型中未知参数的个数。似然函数值越大，说明拟合的效果越好；模型未知参数个数越多，说明模型中包含的自变量越多，模型拟合的准确度就越高，但单纯的以比拟合精度来衡量模型的好坏，肯定会导致未知参数越来越多，自变量以及未知参数的增多就会导致较多的未知的风险。这样一来不仅增加了工作难度，而且估计的精度也会越来越差，所以一个好的拟合模型应该是拟合精度和未知参数个数的综合最优配置。

就一个观察序列而言，序列越长，相关信息就越分散，而且有时候时间序列的相关性衰减，会导致其只适合短息预测。那么要很充分地提取其中的有用信息，通常就需要多自变量复杂模型。以下分别是AIC和SBC准则：

AIC=-2In（模型的极大似然函数值）+2（模型中的未知参数的个数）

中心化的ARMA模型的AIC函数为：

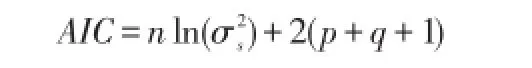
非中心化的为：

中心化的：

非中心化的：

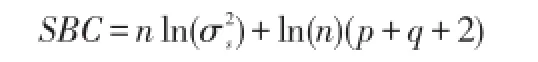
通过比较可以发现，在AIC准则中拟合误差提供的信息要受到样本容量的放大，但参数个数的惩罚因子却和样本没有关系，它的权重始终是常数2，在样本容量趋于无穷大时，它比真实模型所含的未知参数个数要多。SBC将惩罚权重改为样本容量的对数函数，理论上已经证明SBC准则是最优模型的真实阶数的相合估计。

在尽可能全面的范围里考察有限多个模型的AIC和SBC函数值，得出SBC模型是一个相对最优模型。SBC准则的提出，可以有效地弥补根据自相关图和偏自相关图定阶的主观性，在有限的阶数范围内，找到最优拟合模型。因为在自然科学内，规律确实是存在的，且关系是精确的，在相当长的时间内，这些规律关系会保持不变，但在经济领域内则完全是另一回事，经济模式或关系往往与随机噪音交织在一起，改变经济现象的可预测性的因素太多，比如，人类行为的变化无常，某种重大事件的发生等等都会对经济现象有所影响，所以在很多时候，分析数据都依靠分析人员的经验，主观因素非常大，而SBC恰好弥补了这一点，所以说对模型地优化和选择帮助非常大。

检验结果如表所示，检验表明，ARIMA（1，1，0）比ARIMA（0，1，1）相对更优。

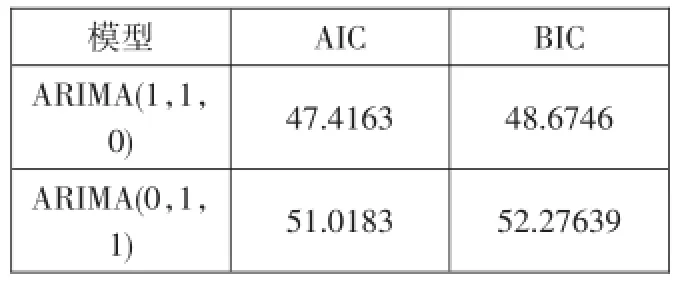
模型ARIMA（1，1，0）ARIMA（0，1，1）AIC 47.4163 BIC 48.6746 51.0183 52.27639

五、模型预测与决策

通过对模型的检验，得到最优模型方程为：1.7426Xt-1-0.7426Xt-2+e=Xt。对模型进行预测得出：最新发布的数据。对比可以得出，8月份的预测精确到了小数点后两位，这一点说明模型相对来说还是比较合适的；9、10月份的预测值则表现出了较大地不一致性，绝对误差表现的很大，但通过相对误差地比较，得出数据仍然在95%的置信区间，说明拟合还是有效的。

根据定性分析和定量分析，可以认识到PPI的下降还将持续，这意味着我国的需求萎缩的状况依然存在。因此，中国工业领域必然会经历一个去产能化的过程，也就是淘汰过剩的产能。所以当PPI下降的时候，不能过度解读为实体经济的收缩，应称之为一次中国工业领域的刮骨疗伤。当前中国工业的过剩产能需要通过低价格来进行市场压缩，否则很难通过行政手段干预。因此，需要提高对经济下行，PPI下降的承受力，从而推动对中国工业产能的控制、产业升级以及结构优化。

六、总结

1.模型的缺陷

ARIMA模型需要历史数据，一般要求不少于50个，然而实际情况是不一定能得到如此多的数据，但是预测还是呈现出越来越准确的趋势。在ARIMA模型中，序列变量的未来值被假定满足变量过去观察值和随机误差值的线性函数关系，可是现实中绝大多数的时间序列都包含非线性关系。

2.遇到的困难

经济指数很容易受各种影响，如果选取的时序样本较长，且波动比较大的时候，很难建立ARIMA模型；同比指数能消除季节性的因素，相比环比数据，建立ARIMA模型更简单；运用较长、波动大的数据时，建立ARIMA的残差序列很难实现非白噪声序列，通常是由于模型对数据信息提取不充分；价格指数不可能永远上涨，它必然是上下浮动的，所以很难进行长期预测。

参考文献

［1］薛冬梅.ARIMA模型及其在时间序列分析中的应用［J］.吉林化工学院学报，2010-6（27）.

［2］王燕.应用时间序列分析［M］.北京:中国人民大学出版社，2005:41-152.

［3］易丹辉.数据分析与Eviews应用［M］.北京:中国统计出版社，2003:106-132.

［4］刘薇.时间序列分析在吉林省GDP预测中的应用［M］.长春:东北师范大学，2008.

［5］田铮译.时间序列分析的理论与应用［M］.北京:高等教育出版社，2003:214-246.

（作者单位：上海理工大学管理学院）

DOI：10.16653/j.cnki.32-1034/f.2016.10.043