数学思想在“图形与几何”教学中的渗透

□ 江苏省常熟市新区小学 吴建英



数学思想在“图形与几何”教学中的渗透

□ 江苏省常熟市新区小学 吴建英

数学思想方法是蕴含于数学知识和内容之中，又高于具体知识和内容的一种理性知识。它是联系数学知识的纽带，也是整个数学知识系统的生命和灵魂，是数学知识赖以转化为认识世界、改造世界能量的桥梁。布鲁纳曾说，掌握基本的数学思想方法能使数学更易于理解和记忆，领会基本数学思想方法是通向迁移大道的“光明之路”。数学思想方法不但对学生学习具有普遍的指导意义，而且有利于学生形成科学的思维方式和思维习惯。

数学思想贯穿于整个小学数学教学的各个领域，在“图形与几何”领域的教学，该如何进行行之有效的渗透呢？下面笔者以“转化思想”、“分类思想”、“集合思想”、“函数思想”为例，简要谈谈自己在教学实践中的一些做法，以期与同行共同探讨。

一、渗透转化思想，培养学生解决问题的能力

转化思想，即不是直接寻找问题的答案，而是寻找一些熟悉的结果，设法将面临的问题转化为某一规范的问题，以便运用已知的理论、方法和技术使问题得到解决。在“图形与几何”领域的教学中，我们通常会把未知问题转化为已知问题，把复杂问题转化为简单问题，把曲线图形转化为直线图形。如在学生掌握长方体、正方体的体积计算公式后，出示一个不规则的铁块，让学生求出它的体积。铁块既不是长方体，又不是正方体，该怎样求它的体积呢？问题一抛出，学生纷纷没了头绪。但由于刚刚解决过教材P23第2题求土豆体积的问题，以及长方体、正方体的体积，学生很快便有了好办法，总体有这样几种：

方法（1）：可以请铁匠师傅帮个忙，让他把这个不规则的铁块熔铸成一个规则长方体后再计算。

方法（2）：把这个铁块放入一个装满水的，且有出水孔的容器，完全浸没在水中，用量杯盛好，看溢出水的体积，就是铁块的体积。

方法（3）：把这个铁块放到一个装有水的长方体的容器内，浸没在水中，量一量长方体容器的长、宽，以及看看水面上升了多少，只要求出长方体容器内上升部分水的体积就得到了铁块的体积。

方法（4）：把铁块放到一个装满水的量杯内，使之淹没，然后拿出来，看看水少了多少毫升，这个铁块的体积就是多少立方厘米。（即同教材“土豆体积”的问题）

引导学生思考：大家的方法都很棒！想想都有什么共同之处？学生的方法要么把铁块的体积转化成了长方体的体积，要么转化成了水的体积，巧妙地利用了转化思想来计算出它的体积。在转化思想的影响下，灵活地将一道生活中的数学问题地用学过的知识来顺利解决了。由此可以看出：学生一旦掌握了转化的数学思想方法，便获得了自己独立解决数学问题的能力。

二、渗透分类思想，提高学生概念建构的能力

分类思想是一种基本的数学思想方法。分类通常是指一种揭示概念外延的逻辑方法，也就是以比较为基础，按照事物间性质的异同，将相同性质的对象归入一类，不同性质的对象归入不同类别的过程，分类也称为划分。小学阶段，儿童以形象思维为主，认知水平不高，其最大的特点是思维离不开具体事物的支撑。分类必然存在分类对象，满足了学生的认知需要形象支撑的特点。在图形教学中渗透分类的数学思想，教师不能仅仅满足于让学生得到分类的结果，而应引导学生理解为什么要这样分类，交流是按怎样的标准进行分类的，讨论怎样分类较为合理。教师要引导学生对分类的结果进行解读，充分展现学生的思维过程。如在教学“认识平行”时，我设计的第一个环节是从生活情境中选取五张图片，从每张图片中抽象出两条直线：

让学生通过观察、分析、比较，把5组直线的位置关系进行分类。学生通过交流，出现以下几种分法：

A②⑤两条直线交叉了（连在一起），①③④两条直线是分开的。

B②④⑤两条直线交叉了，①③两条直线是分开的。

C②⑤两条直线交叉了，①③两条直线是分开的，④另外分一类。

为什么这样分？你是按怎样的标准来分类的？请不同分法的学生说说想法。

直线可以无线延长，我们把它延长！（课件演示延长）

问：相交吗？（再延长）问：相交吗？（再延长）问：相交吗？好，让我们闭上眼睛，想象一下，这两条直线无限延长以后，会相交吗？（课件演示延长相交）

告诉学生：像这样互相交叉（或连在一起）的两条直线，它们的位置关系，在数学上叫做“相交”。那么，像②④这样的两组直线，它们相交吗？揭示：像这样不相交的两条直线我们说“互相平行”。

类似这样的教学活动，让学生经历从分类中产生矛盾，在充分辨析中化解矛盾，“平行”的本质逐渐清晰，概念的引入趋于无痕化。

三、渗透集合思想，提升学生知识梳理的能力

集合间的包含关系在小学数学教学中的渗透主要表现在概念系统的构建之中。英国数学家维恩最早使用了可以用于表示任意的几个集合（不论它们之间的关系如何，都可以画成同一样式）的“韦恩图”，用韦恩图表示集合，有助于探索某些数学概念的本质属性。如新教材第8册，有关三角形的分类问题，除用文字说明外，还用集合形象地表示出来。我在教学“三角形的分类”一课中，安排了这样一个环节：

在认识了三角形按角分，可以分为：直角三角形、锐角三角形、钝角三角形三种三角形后，给出一个椭圆形，引导学生想：如果我们把所有的三角形看作一个整体，用一个椭圆表示（课件演示），按上述三角形的分类，你能在这个椭圆里表示出这三种三角形吗？你能在练习纸上画一画，写一写吗？让学生独立在练习纸上画一画。学生大致出现这三类结果：

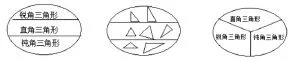
我肯定了这几个学生的方法，同时课件出示书上的韦恩图，并告诉学生：通常，为了更美观、更科学，数学上用这样的图来表示三种三角形的关系。从这个图上可以看出，这三种三角形都是这个整体的一部分。还让学生闭上眼睛，把这幅图记在脑子里，使学生看清三角形集合与锐角三角形、直角三角形和钝角三角形各集合之间是整体与部分的关系。

四、渗透函数思想，展现学生探究发现的能力

函数的思想方法就是运用运动和变化的观点、集合和对应的思想去分析问题的数量关系，通过类比、联想、转化合理地构造函数，运用函数的图象和性质，使问题获得解决。函数的思想方法是最重要、最基本的数学思想方法之一。

虽然在小学数学中没有正式引入函数概念与函数关系式，但这不等于没有函数的雏形、没有函数思想的存在。在小学阶段渗透函数思想方法，可以使学生懂得一切事物都是在不断变化、而且是相互联系与相互制约的，从而了解事物的变化趋势及其运动的规律。这对于培养学生分析和解决实际问题的能力都有极其重要的意义，而且可以为学生以后进一步学习数学奠定良好的基础。如六年级长方体和正方体单元中，有这样一道题：

丹丹用24个棱长1厘米的小正方体摆出了一个长方体。她摆成的这个长方体的长、宽、高各是多少厘米？在下表中列出各种不同的可能（表略）。

在各种不同的摆法中，表面积最小的是哪一种？

学生不难得到结果：

在解决这一类问题时，大多数学生都能准确找到答案，但也有一部分学生会有重复和遗漏。于是，我通常会引导学生这样有序地思考：当24个小正方体全部排成一层（即高是1cm）时，会有哪几种摆法？学生想摆成一层，全部排成1排（即宽是1cm）时，每排几个？摆成一层，全部排成2排（即宽是2cm）时，每排几个？摆成一层，全部排成3排（即宽是3cm）时，每排几个？当摆成2层呢，又有哪几种摆法？

在研究过程中，学生会渐渐地感悟到：要想得到最小的表面积，就要把所有能摆成的长方体逐一例举出来再比较；而要想得到不同的长方体，必须在保持体积（即小正方体的个数24个）不变的情况下改变长方体的长、宽、高。在高不变的情况下，宽逐渐变大，长就逐渐变小。同时，也在这些数据的变与不变中发现：当长、宽、高三个数据最接近时（即越接近正方体时），表面积最小。这样就把“静态”的学习变成了“动态”的研究，而这种由“静”到“动”的过程就是函数的本质，也体现了极值思想。

因此，是函数思想使学生学习的过程“动”了起来，使学生的学习“主动”起来，学生愿意去发现规律，并尝试将规律表述出来，这样也有助于培养学生自主探究的能力。