我国上市商业银行风险溢出评价与宏观审慎监管

张天顶　张宇

(武汉大学经济与管理学院，湖北武汉430072)



我国上市商业银行风险溢出评价与宏观审慎监管

张天顶张宇

(武汉大学经济与管理学院，湖北武汉430072)

摘要：随着金融自由化程度的不断提高，金融系统在分散风险和促进资金自由流动的同时也加大了风险的传染性和破坏性。文章采用我国16家上市商业银行的日度收盘价数据，结合GARCH-混合Copula-CoVaR模型对其风险溢出效应进行定量估计。与仅采用单一的Copula方法相比，混合Copula更能够捕捉到市场在不同状态下单个机构与金融系统之间的相关性。研究结果表明，在横截面维度上，“四大”国有银行在我国银行体系中处于系统重要性地位，同时股份制商业银行民生银行、中信银行和交通银行在测量结果中处于相对重要的地位，也需要引起金融监管者的高度重视；在时间维度上，到2015年，随着我国股票市场出现的剧烈震荡，银行业系统性风险呈上升趋势，对此监管者需要制定相应政策以防发生系统性风险。

关键词：风险溢出效应；系统性风险；系统重要性金融机构；GARCH-Copula-CoVaR

一、引言

2007年爆发的全球性金融危机使得金融监管者逐渐意识到在系统性风险爆发时，金融风险的传染性和溢出效应所造成的破坏力。系统性风险通常由某个诱导因素引起，继而导致不稳定性在整个金融系统内扩散，威胁到金融系统的稳定和安全，进而对实体经济造成严重的损害(卜林，2015[1])。由于风险溢出效应放大了单个金融机构或某一金融子市场对整个金融体系的冲击效应，科学测度不同金融机构的风险溢出效应就成为系统性风险研究的一个重要内容。本文将对我国上市商业银行的风险溢出效应进行度量，现有研究表明，与证券、保险和信托行业相比，我国银行业的风险溢出效应要更大(沈悦，2014[2]；徐映梅，2015[3])，因此对我国商业银行系统性风险的度量就显得更加重要。

基于公开市场交易数据度量系统性风险的方法由于其数据上的可获得性，受到越来越多研究者的青睐，其中以条件在险价值CoVaR法运用最为广泛(Adrian，2011[4]；周强等，2014[5])。目前主流的CoVaR估计方法有分位数回归法、二元GARCH拟合法以及引入Copula联结函数的方法。分位数回归的方法提出时间最早，然而它并不能完全捕捉到金融机构财务数据内在的“尖峰厚尾”特性，且无法刻画序列之间的非线性关系，本文引入混合Copula模型较好地解决了这一缺陷。国内学者也有基于Copula模型的研究，但是这些研究采用的Copula函数相对较为单一，往往只能捕捉到市场在某一种情况下的序列相关性，且该模型主要用于度量不同市场之间的风险溢出效应，用于度量银行机构风险溢出效应的研究并不多见。

二、 相关文献评述

(一) 金融机构风险溢出效应

随着金融自由化程度的不断提高，金融系统在分散风险和促进资金自由流动的同时也加大了风险的传染性和破坏性，使得现代金融危机呈现出波及面更广、危害力更强的特点。2007年爆发的全球性金融危机使得人们日益地意识到：传统地关注单个金融机构的微观审慎监管并不足以有效地防范整个金融体系的系统性风险，在金融监管过程中，我们不能“只见树木、不见森林”。金融危机爆发之时，由于单个金融机构的危机造成的风险和恐慌将在不同金融机构之间蔓延，进而对整个金融系统造成极大的威胁。随着风险传染性和溢出程度的不断加深，将极有可能触发系统性风险，导致整个金融市场的瘫痪，进而对实体经济的信贷供给产生负面影响(Adrian等，2011[4])。事实上，2007年以美国贝尔斯登两只基金破产为危机起始点，雷曼兄弟倒闭事件等相继爆发，投资银行体系受到重创；2010年由于冰岛三大国有银行宣布破产，英国、德国等欧洲银行业受到严重亏损，欧洲国家主权债券评级全面下调。可见，随着金融不断创新和自由化，金融机构的风险不仅受其自身因素的影响，还受其他金融机构风险的冲击，这种机构之间的风险波动传导机制即为风险溢出效应(李志辉等，2011[6])。

随着金融一体化程度的加深，金融机构之间的相关性越来越高，从理论上对金融机构的风险传染机制进行分析就显得尤为重要。Adrian等(2011)[4]认为，在系统性金融事件爆发时，金融机构之间的风险传染性和溢出效应既有可能是由金融机构之间存在直接的契约关系，使得彼此成为高度依赖的信贷风险交易对手而直接导致，同样也有可能由于金融机构均暴露于同样的市场风险因子当中而间接造成。具体到银行业中，在危机刚开始时，可能只是单个银行机构的经营失败，但是由于现代金融机构之间日益复杂的相关性和复杂度，一旦处于系统重要性地位的金融机构发生危机，由于其在整个市场中的重要地位，将会对市场产生负的外部性，恶化银行所处的环境。同时，由于银行具有同质性的经营行为，暴露于同样风险因子中的银行机构将同样面临较大的周转困难。一旦市场上关于银行的传闻开始蔓延，投资者对银行缺乏信心，导致流动性供给收紧。这种信息的溢出效应会加剧市场波动，导致流动性供给的进一步枯竭，从而在资本市场上间接地加大了风险造成的损失，结果是金融机构将面对市场流动性和资金流动性迅速的枯竭，以及市场上增加的波动性。在当今经济金融化的背景下，虚拟经济与实体经济相互作用，金融市场上急剧增大的波动性也会使得实体经济融资变得困难，从而造成市场环境的恶化。

(二) 风险溢出效应的度量

由于风险溢出效应放大了单个金融机构或某一金融子市场对整个金融体系的冲击效应，科学测度不同金融机构的风险溢出效应就成为系统性风险研究的一个重要内容。传统的在险价值VaR分析法简单明了，但其忽略尾部风险且不具次可加性等缺陷使其在关注市场尾部风险的系统性风险度量中存在较大缺陷，Adrian等(2011)[4]提出的CoVaR法有效地改进了这一问题。CoVaR衡量的是当一个机构处于其在险价值的条件时另一个机构的市场表现，具体来讲，将金融系统视为各金融机构的资产组合，那么单个金融机构的CoVaR等于其处于在险价值情况下的市场表现与其处于中性状态下的市场表现之差，因此可以用于衡量该机构对整个市场的风险贡献程度。

目前，CoVaR的度量方法主要有基于分位数回归的方法(Castro等，2014[7]；陈守东等，2014[8])，基于二元GARCH模型的方法(Girardi等，2013[9])，以及引进Copula联结函数的方法(Reboredo等，2015[10])。基于分位数回归的方法通过引进如市场波动率、流动性利差、消费者价格指数等宏观经济变量将宏观审慎与微观审慎结合起来，然而简单的分位数回归并不能完全捕捉到金融数据“尖峰厚尾”的特性，且无法刻画序列之间的非线性关系，采用Copula联结函数可以有效地弥补这一方面的不足。Copula函数是由Sklar(1959)[11]提出的一类将联合分布函数与各自边缘分布函数联结起来的函数，由于其刻画边缘分布的灵活性和刻画相关关系的多样性优势而在20世纪90年代以来得到迅速发展，并在风险管理、投资组合等领域有着广泛的运用(吴海龙等，2013[12])。然而目前国内研究对于Copula函数的选择较为单一，往往不足以捕捉到市场朝不同方向变化时的联结情况，且其主要运用于股票市场的风险溢出或国内金融行业之间的溢出效应上，直接运用于我国上市银行系统重要性的度量较少。本文引入混合Copula函数有效地捕捉到市场在利好和利空等不同情况下金融时间序列之间的相关关系，并引入期望最大化EM算法对其参数进行估计，从而与传统仅基于极大似然法的参数估计相比更具稳健性。从结果来看，本文采用的GARCH-Copula-CoVaR模型的度量方法对我国上市银行的系统重要性分析是一项有益的补充。

三、 研究方法

(一)CoVaR方法介绍

单个金融机构的CoVaR是指当该机构发生危机时整个金融系统此时的在险价值。假设Xi为该机构的收益率，Xj为金融系统的收益率，则该机构的VaR和CoVaR可分别用式(1)和式(2)表示

(1)

(2)

其中，α和β为置信度。可以看出式(2)是一个条件概率公式，采用贝叶斯公式可将其变换为式(3)所示

(3)

注意到式(3)中分母即为在险价值的置信度，因此可将其变换为式(4)

(4)

以上是一个联合概率密度函数形式，根据Sklar定理[11]，引入Copula函数可将联合概率密度函数转换为边缘概率密度函数的联结函数形式，表达为式(5)

(5)

由此可见，CoVaR的求解可采用如下的两步估计法。

第一步，对序列的边缘分布进行拟合，得到其概率分布后，选取适当的Copula函数并对其参数进行估计，根据Copula函数的形式求出u值；

第二步，根据Xj的边缘分布的反函数，得到CoVaR=F-1(u)。

为更准确地衡量单个金融机构对系统的风险贡献程度大小，需要对进行去量纲处理，因此引入新指标pCoVaR，其定义如式(6)所示

(6)

本文采用GARCH(1,1)-偏t模型对收益率序列的边缘分布进行拟合，采用混合Copula函数刻画金融机构与金融系统收益率之间的相关关系。

(二) 边缘分布的拟合

金融时间序列呈现出的波动率聚集的特性要求对其边缘分布的拟合需要有效地刻画出其条件异方差性，而同时其呈现出来的“尖峰厚尾”的特性说明传统基于正态分布的假设往往并不合理。本文采用GARCH-偏t分布，大量的实证结果表明采用GARCH(1,1)模型能够很好地刻画出金融时间序列的“尖峰厚尾”及条件异方差的特性[2-3]，而与国内其他研究常采用的GARCH-学生t分布不同，本文采用的偏t分布是在传统t分布的基础上加入一个偏度参数η，能够更加准确地描述金融资产序列的非对称性和厚尾性，与金融时间序列的有偏特性相契合。其模型如式(7)所示

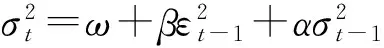
(7)

其中，rt表示收益率序列，μ为收益率均值，εt为残差，σt表示波动率，It-1为t-1时刻的信息集，残差vt服从偏-t分布，其分布函数如式(8)所示

(8)

(三) Copula函数的选择

Copula函数形式多样，最常见的两大家族包括Elliptical-Copula和Archimedean-Copula。其中Archimedean-Copula函数由于其简单易用而得到广泛应用，其函数族形式满足

C(u1，u2…up)=φ-1{φ(u1)+φ(u2)+…+φ(up)}

(9)

Archimedean-Copula函数族中又以Clayton、Frank和Gumbel三种使用最为广泛，表1介绍了这三种函数的基本形式。

注：作者根据Yan(2007)[13]整理所得。

Clayton-Copula函数分布呈下尾高上尾低的L型，即说明分布的下尾有很强的相关性，能够较好地刻画出市场利空时候的相关性；Gumbel-Copula密度分布呈上尾高下尾低的丁字型，说明该分布的上尾部具有很强的相关性，而下尾部是渐进独立的，能较好刻画市场利好时候的时序相关性；Frank-Copula具有对称性，无法捕捉到随机变量之间非对称的相关关系。由于我国股票市场在近年来都出现了较大的波动，采用单个Copula函数将无法很好地捕捉到市场朝不同方向震荡时的相关关系，因此本文采用混合Copula，用三种Copula函数的线性组合来刻画单个机构与金融系统之间的相关性，其函数形式如式(10)所示

Mixcopula=w1·Clayton+w2·Frank+w3·Gumbel

(10)

其中w1、w2和w3分别为各自Copula的权重。

在确定Copula函数的形式之后，就需要对其中的参数进行估计。然而由于参数较多，直接采用极大似然估计法比较困难且结果不具稳健性，因此本文引入期望最大化EM算法对参数进行估计。EM算法是由Dempster于1977年提出的一种参数极大似然估计方法，它本质上是一种迭代算法。通过引入一个隐含变量，将不完整数据的似然函数最大化问题转换为完整数据的似然函数最大化问题求解，通过不断迭代找到局部最优解。具体来讲，当我们不知道样本属于哪一个Copula的时候，引入隐含变量zk，当其属于第k个Copula时，zk=1，否则，zk=0。此时完整数据的对数似然函数可以表示为式(11)

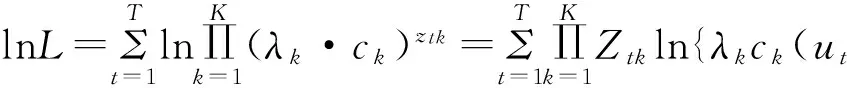
(11)

其中ck为第k个Copula的概率密度函数，λk为其权重，ztk为第t个样本在第k个Copula函数的隐含值，ut为样本累计分布函数，θck为第k个Copula的参数。

EM算法主要分为以下两步

E(Expectation)步骤：求期望，即计算隐含变量的取值；

M(Maximization)步骤：最大化似然函数并对参数进行更新。

在估计出相应参数之后，混合Copula的函数形式如下式所示

(12)

在上式中，w1、w2、w3分别代表Clayton、Frank和Gumbel函数的权重，α1、α2、α3分别为各自Copula函数的参数，均为已知，因此上式只有一个自变量。直接对该方程求解析解较为困难，考虑到Copula函数本身是随自变量单调递增且u服从[0,1]上的均匀分布，根据这一特性将会很容易地求出u的数值解。将求解出来的u代入边缘分布的反函数中将能很快得到其CoVaR值。

四、 实证结果及分析

(一) 数据描述

本文采用2010年9月2日至2015年7月31日，我国16家上市商业银行的每日前复权收盘价，共1 191个数据观测值进行分析，数据来源Wind数据库。

假设R和Rsys分别代表单个银行和整个上市商业银行系统的日度收益率，则有

(13)

(14)

表2是对16家上市银行和银行系统的收益率进行的描述性统计。

从表2可以看出，所有时间序列的偏度均不为0，且其峰度较大，这符合金融时间序列“尖峰厚尾”的特性。为检验其是否存在条件异方差性，接下来对各时间序列进行正态性检验、平稳性检验和ARCH效应的检验，检验结果如表3所示。本文采用JB检验值检验收益率序列的正态性，由表3可知，所有的收益率序列的正态性检验p值都小于0.05，因此有理由认为所有的收益率序列均不服从正态分布(用Shapiro-Wilk检验结果相同)。

采用单位根ADF检验来检验序列平稳性，可以看出，所有的ADF-p值均小于0.05，即拒绝接受收益率序列自回归中存在单位根的假设，因此可以认为收益率序列平稳。

最后，由于要对收益率序列进行GARCH拟合，因此要进行ARCH效应的检验。采用拉格朗日极大似然LM检验，可以看出所有的序列都具有强烈的ARCH效应，因此采用GARCH模型对序列的边缘分布进行拟合显得合理。

(二) 实证结果分析

如前文所述，GARCH(1,1)-偏t分布能较好对收益率序列进行拟合，结果如表4所示。

由GARCH模型的设定可知，如果模型的拟合是充分的，则其得到的标准化残差将服从独立同分布。本文通过对模型的标准化残差及其平方项绘制ACF和PACF图，对GARCH模型的拟合进行充分性检验。如果模型的拟合是充分的，则残差项不会出现自相关及异方差效应。以工商银行为例，其标准化残差及平方项的ACF和PACF图如图1所示，可以看出，本文采用的GARCH(1,1)-偏t分布对收益率序列的边缘分布拟合效果良好。

由于Copula函数的特点，采用收益率序列和采用残差序列对Copula参数的拟合结果是一致的，因此可根据上述边缘分布的拟合残差对选定联结函数进行参数拟合。本文采用混合Copula函数来描述序列之间的相关关系，但在此之前，首先采用单个Copula对单个银行与银行系统之间的相关关系进行描述，以便进行稳健性比较。根据极大似然法对参数进行估计，并用AIC准则对不同模型反映的信息程度进行比较，结果如表5所示。

注：作者整理所得，此处仅以工商银行为例。若需要更多收益率序列的ACF及PACF图可与作者联系。

根据AIC信息准则，可以看出与另外两种函数相比，Gumbel-Copula对序列相关性的拟合效果更优(其AIC值更小)。正如前文所述，Gumbel-Copula能够较好地捕捉到市场利好状况下金融序列之间的相关性。在本文样本研究期间，我国上证综指指数虽有短期震荡，但总体而言呈现出震荡上升的趋势，因此Gumbel-Copula函数能够较好地捕捉到这一特性。

在估计出Copula参数之后，通过计算式(5)中的u值并将其代入边缘分布的反函数，可直接得到单个银行的CoVaR及pCoVaR，如表6所示。

注：d-copula表示该copula函数对应的CoVaR值，p-copula表示其对应的pCoVaR值，用百分数表示。

由表6可以看出，用单个Copula度量出来的结果均显示，工商银行、中国银行、农业银行和建设银行四大国有银行的pCoVaR值较大，因而在我国上市银行系统中处于系统重要地位。此外，我们可以观察到，这三种方法度量出的系统重要性排序几乎完全一致，因而结果具有较好的稳健性。

由于单个Copula只能捕捉序列处于单个方向变动时的相关性，而无法对市场多种变化时收益率序列的相关性进行充分刻画。因此接下来我们采用混合Copula对银行个体及系统之间的序列相关进行拟合。如前文所述，本文采用期望最大化EM算法对混合Copula进行稳健的参数估计，其结果如表7所示。通过将表7中混合Copula与表5中单个Copula的AIC准则对比可以看出，采用混合Copula的AIC值更小，从这一角度来看其拟合效果更佳。

在得到混合Copula的各参数估计值之后，根据式(12)可以求解出u值，再将其代入到边缘分布的反函数中，即可得到CoVaR及pCoVaR值，结果如表8所示。至此，可以根据单个Copula拟合及采用混合Copula对我国商业银行的系统重要性进行排序，其结果对比如表9所示。

由表9可以看出，采用不同Copula函数的系统重要性排序之间的稳健性较好。总体上来看，大型国有银行如工商银行、中国银行、建设银行和农业银行在我国均处于系统重要性地位，它们的活动将会对我国银行系统产生重要的影响，因此在监管过程中需要对这些银行进行密切关注并要求更多的信息披露。此外，由于目前尚无统一标准来确定系统重要与非系统重要之间的明确界限，根据周小川[7]提出的要关注的D-SIFI系数的思想，除“四大”国有银行外，还需关注与交通银行系统重要性指标接近的银行。经过分析可以看出，在交通银行之上还有股份制银行如民生银行、中信银行等也同样可认为处于系统重要地位，因而在监管政策的制定过程中也应该给予密切关注。

(三)系统性风险的动态变化及其对宏观监管的启示

在宏观审慎政策制定过程中，监管者不仅要在横截面维度上关注某一时刻的不同银行的系统性风险相对大小，同样还需在时间维度上关注其随时间的变化趋势，即强调系统性风险的动态性。根据本文采用的GARCH-Copula-CoVaR模型，可以得到各商业银行pCoVaR值的时变特征，图2为对我国普遍被认为是系统重要的“四大”国有银行的pCoVaR值绘制的时序图。

注：dMixCoVaR和dMixCoVaR50%分别表示在银行处于VaR5%状态和正常状态下系统的CoVaR值. pMixCoVaR是对应的pCoVaR值。

由图2可知，截止到2015年，“四大”国有银行的条件在险价值普遍上升，说明整个银行业的系统性风险处于逐步上升态势，监管当局要予以特别关注。同时，本文实证结果表明，民生银行、交通银行及中信银行在我国商业银行系统中处于相对重要地位，同样需要引起监管者的密切关注。为描述这三家银行对我国商业银行体系的系统性风险贡献程度的变化特征，可将这三家银行与工商银行的pCoVaR值对比作时序图，如图3所示。

对比图2和图3发现，“四大”国有银行的pCoVaR的时变特征十分相似，且各自之间的相关性非常大，而被本文认为处于系统相对重要地位的民生银行、交通银行和中信银行的pCoVaR值变化相关度虽不如“四大”国有银行之间那么高，但其整体变化趋势与“四大”国有银行的变化趋势是高度吻合的。因此，在监管过程中加强这三家银行的关注显得很有必要且极具现实意义。事实上，面对当前银行系统较高的系统性风险，我国监管当局也在不断丰富宏观审慎管理工具，积极面对和防范系统性风险。2014年5月，由中国人民银行牵头出台的《关于规范金融机构同业业务的通知》，切实有效地采取措施规范同业业务发展，增强了我国金融系统稳健性；银监会近两年相继通过了《商业银行全球系统重要性评估指标定义说明》、《商业银行流动性风险管理办法(试行)》，旨在对我国系统重要性机构进行有效监管，增强银行体系应对风险的能力。

五、主要结论与启示

本文研究结果表明：(1)采用混合Copula模型的AIC信息准则比采用单个Copula模型得到的AIC准则要小，说明本研究在方法上是对传统方法的有效改进，混合Copula能够更为有效地度量市场朝不同方向变化时单个金融机构与整个金融市场之间的相关关系；(2)横截面维度上，“四大”国有银行在我国银行系统中处于系统重要地位，但同时民生银行、中信银行和交通银行处于相对系统重要地位，也需要得到监管者的高度重视；(3)时间维度上，CoVaR的动态变化表明，进入到2015年，面对我国股市的剧烈震荡，我国银行业系统性风险不断上升，政策制定者在金融监管的过程中要特别注意系统重要性银行的活动，以防发生系统性风险。

根据宏观审慎的政策框架，本研究认为监管者需要在现阶段有意识对系统重要银行的规模、关联度、复杂性及跨地区活跃度进行限制，并时刻注意这些银行是否存在道德风险。同时也要密切关注系统重要银行的流动性覆盖率和流动性比率，判断其是否有足够的能力吸收可能性损失，同时进一步推进系统重要银行风险管理小组的成立，并对其运转状况做更多披露。分别在事前、事中、事后等不同层次采取相应措施，防范系统性风险的发生。

参考文献

[1]卜林, 李政. 我国上市金融机构系统性风险溢出研究——基于CoVaR和MES的比较分析[J]. 当代财经, 2015(6):55-65.

[2]沈悦, 戴世伟, 罗希. 中国金融业系统性风险溢出效应测度——基于GARCH-Copula-CoVaR模型的研究[J]. 当代经济科学, 2014, 36(6):30-38.

[3]徐映梅, 徐璐. 中国金融业跨市场风险测度与分析——基于GARCH-Copula-CoVaR模型[J]. 统计与信息论坛, 2015,30(4):28-32.

[4]Adrian T, Brunnermeier M K. CoVaR [R]. New York: NBER Working Paper, 2011.

[5]周强,杨柳勇. 论中国系统重要性银行识别——市场模型法还是指标法[J]. 国际金融研究, 2014 (9): 70-79.

[6]李志辉, 樊莉. 中国商业银行系统性风险溢价实证研究[J]. 当代经济科学, 2011, 33(6):12-20.

[7]Castro C, Ferrari S. Measuring and Testing for the Systemically Important Financial Institutions[J]. Journal of Empirical Finance, 2014,25(3):1-14.

[8]陈守东, 王妍. 我国金融机构的系统性金融风险评估——基于极端分位数回归技术的风险度量[J].中国管理科学, 2014, 22(7): 10-17.

[9]Girardi G, Ergun T. Systemic Risk Measurement: Multivariate GARCH Estimation of CoVaR[J]. Journal of Banking and Finance, 2013,37(8): 3 169-3 180.

[10]Reboredo J C, Ugolini A. Systemic Risk in European Sovereign Debt Markets: A CoVaR-Copula Approach[J]. Journal of International Money and Finance, 2015,51(12):214-244.

[11]Sklar A. Functions de Repartition and Dimensions et Lears Marges[J]. Publications de I’Institut Statistique de I’Universite’de Paris. 1959,32(1): 229-231.

[12]吴海龙, 方兆本,朱俊鹏. 基于R-Vine Copula方法的投资组合风险分析[J]. 投资研究, 2013, 32(10): 98-107.

[13]Yan J. Enjoy the Joy of Copulas: With a Package Copula [J]. Journal of Statistical Software, 2007, 21(4): 1-21.

责任编辑王丽英

Risk Spillover of China’s Listed Commercial Banks and Macroprudential Implications

ZHANG Tian-ding, ZHANG Yu

(Economics and Management School, Wuhan University, Wuhan 430072, China)

Key words：risk spillover; systemic risk; Systemic Important Financial Institutions (SIFI); GARCH- Copula-CoVaR

Abstract：With the development of financial liberalization, financial system plays an important role in risk diversification and funding liquidity, while at the same time accelerates risk contagion and spillover. This paper makes use of the daily close price of the 16 listed commercial banks to estimate their risk spillover based on GARCH-Copula-CoVaR model. Compared to using single Copula, Mixed Copula have advantages in capturing the correlation between individual financial institution and the financial system under different circumstances. The results show that in the cross sectional analysis, the big four state-owned banks are systemic important in China’s banking system, meanwhile some joint-stock commercial banks such as China Minsheng Bank, China CITIC bank and the Bank of Communications are relatively systemic important, and thus the regulators’ high attention should be paid to these facts. In a time series view, the systemic risk of banking sector arises with the volatility of China’s stock market when entering 2015, which calls for regulators proposing corresponding policies to mitigate systemic risk. All these conclusions provide empirical support for China Banking Regulatory Commission to make macroprudential policies.

收稿日期：2016-03-27

基金项目：国家自然科学基金项目(71203168)；国家社科基金重大项目(15ZDC020)。

作者简介：张天顶，男，武汉大学经济与管理学院副教授，主要从事国际宏观经济与金融研究；张宇，男，武汉大学经济与管理学院硕士生，主要从事金融市场系统性风险研究。

中图分类号：F832.33

文献标识码：A

文章编号：1005-1007-(2016)07-0080-12