网络结构、危机传染与系统性风险
2015-05-04石大龙白雪梅
石大龙 白雪梅


摘 要:异质的金融网络结构中,危机传染效应所引起的系统性风险不同。本文基于复杂网络理论,研究随机网络、小世界网络和无标度网络这三种金融网络中危机传染对系统性风险的影响。首先构建有向加权的银行间随机网络、小世界网络和无标度网络,并根据网络结构确定网络中每个银行的资产负债表。其次模拟分析两类随机冲击和两类目标冲击下,不同网络结构中风险传染所引起的系统性风险状况。结果显示:无标度网络面对冲击时的稳定性更高,但当连接最多的银行遭受冲击时,这种网络结构极端脆弱;随机网络面对目标冲击具有最高的稳定性,但面对随机冲击则更加不稳定;金融网络呈现出“稳健而脆弱”的特性。
关键词:网络结构;危机传染;系统性风险;复杂网络理论
中图分类号:F8309 文献标识码:A
文章编号:1000176X(2015)04003109
一、引 言
近年来,国际上金融机构失败所引起的系统性危机揭示了系统性风险的重要性。系统性风险是影响整个金融系统稳定的宏观层面的风险,而不是系统中某个个体的风险。一般来说,系统性风险源于三种负面冲击的影响:一是宏观经济层面负面冲击,例如,经济增长、失业、通货膨胀等的冲击;二是利率、汇率的大幅波动以及资本市场价格下降等负面冲击的影响;三是金融系统内的危机传染。危机传染是系统性风险积累和爆发过程中十分核心的一个环节[1-2]。某一金融机构的失败会通过传染影响整个金融系统的稳定。金融危机期间,一个银行可能无法按时足额支付所有的债务,这会给债权人造成一定的损失。如果这个损失的金额超过了债权人的资本,那么将导致债权人的一些短期债务出现违约。进而又导致债权人遭受资产损失,并导致一系列的债务违约。这种连锁反应可能最终导致整个金融系统的崩塌,而金融危机的溢出效应又会引致严重的经济危机。随着经济金融全球化的进一步发展以及金融自由化进程的加快,金融系统内各类金融机构间通过互相持有资产负债、持有同类资产等形式形成各种金融网络。近年来,金融网络中的危机传染与系统性风险以及金融稳定的关系已成为金融理论研究和应用研究的热点话题之一[3-4]。许多学者逐渐使用网络科学理论来解释金融网络中的危机传染机制,并探讨何种金融网络结构更容易促使金融稳定。其中最主要的一个共识是:银行等金融机构间相互联系形成的金融网络能够传导和放大任一机构所遭受的冲击。换言之,危机传染的广度和深度与银行和金融机构间相互联系的网络拓扑结构密切相关。
Allen 和Gale[5]通过拓展Diamond和Dybvig的银行挤兑模型(bank-run model),开创性地研究了网络结构如何通过传染来影响系统性风险或金融稳定,他们发现,银行系统内更高的连接度更不容易导致银行挤兑。此后,众多学者从不同的角度拓展了Allen 和Gale的模型,这些模型均认为网络的不完备性会增加系统性风险,而且不完备的网络是事后次优的,不过,金融网络的完备性只是金融系统稳定的充分条件[6]。而事实上大部分金融网络都是不完备的,但其传染的概率却可能很低。早期的此类模型多是基于简单的网络模型,分析金融网络中的风险传染问题,一般将此类模型称之为程式化模型。近期基于复杂网络理论的金融网络模型则以更精确的方法论证了网络连接性如何影响系统性风险以及金融稳定性,均发现金融系统呈现出“稳健但脆弱”的特性:在正常时期,银行间的联系可以加强流动性配置,提高金融机构间的风险分担;而危机期间,通过在系统中的传染,相同的连接程度会放大风险。特别是连接性与负面冲击的规模相互作用会导致金融系统从稳定状态突变为不稳定状态[7-8],而且,当金融网络中同业资产和负债的规模非常大时,完备的金融网络甚至可能会损害系统稳定性[9]。此类运用复杂网络理论的模型假定较为严格,其不合理之处主要体现在:一是没有考虑金融机构不同维度上的异质性对风险传染和系统性风险的作用;二是没有考虑金融市场中的信息不完全对传染和金融系统稳定的影响;三是没有考虑金融机构的不正当行为对传染和系统性风险的影响。
我国学者也对金融网络中的传染效应问题展开研究。马君潞等[10]采用银行资产负债数据估算我国各银行间的双边风险敞口头寸,分别考察单个银行破产与多个银行同时破产所造成的传染效应。范小云等[11]通过构建网络模型考察银行间的关联性对系统性风险的影响。他们发现,相比银行规模,银行间的关联程度,尤其是负债关联性较高的银行更容易诱发系统性危机,而且其破产造成的损失也更大。高国华和潘英丽[12]分别估算了流动性风险和信用违约两种情况下传染所造成的资本损失,并考察了不同的银行间网络结构对传染效应的影响,发现分散型市场中的传染风险比相对集中型市场中的传染风险要小。此外,他们研究了影响银行系统重要性和易受传染性的影响因素,发现银行类型、资产规模、风险头寸是影响银行系统重要性的因素,而银行类型、风险暴露程度和资本充足状况则是影响银行易受传染性的因素。刘冲和盘宇章[13]指出,银行间同业拆借网络存在两种相反的效应:一是为传染提供了渠道;二是通过风险分担推动了金融稳定。他们通过理论模型证明,在异质性流动冲击下,同业拆借网络的风险分担效应占据主导地位,它能够保证银行免受清算长期资产的损失,因而能够有效降低传染的概率,有助于维护金融稳定。并以1935年“白银风潮”作为异质性流动冲击,采用此期间上海银行间的同业拆借数据验证了有效的银行间拆借网络能够维护金融系统稳定。
现有文献着重探讨个体失败为什么会导致系统性风险,主要结论是:在一定的假设条件下,个体失败会通过金融网络的传染效应影响整个金融系统的稳定性。而且,这种影响几乎都是非线性的,这意味着必须十分小心地实施减小系统性风险强度和范围的政策,特别是当今金融全球化高速发展成为普遍的潮流,全球经济体已形成一个相互依赖的网络。那么,在这种日益复杂的金融网络中,传染究竟通过何种途径、以何种形式影响整个金融系统的稳定性,这种影响的程度又有多大?这些正是本文需要解决的问题,也是本文的价值所在。
二、金融网络中的传染与系统性风险:理论模型
系统性风险有广义和狭义之分,通过银行间市场的传染效应所引起的系统性风险即是狭义的系统性风险。而现代金融体系中,大量的金融中介通过相互借贷、持有共同资产等方式相互联系,形成一个复杂的网络结构。信用违约掉期(CDS)和债务抵押证券(CDO)等复杂的金融衍生品则进一步加剧了这种联系的复杂程度。金融机构间的这种相互依存关系会导致一个很小的负面冲击得以在复杂的金融体系中传播并放大,并最终危害整个金融体系甚至宏观经济运行的稳定。雷曼兄弟公司破产和美国国际集团(AIG)困境就是对此最真实的诠释。金融机构间的这种复杂的联系也导致难以评估困境下金融机构行为或直接违约所引起的潜在传染效应。
近年来,大量研究关注金融体系中的负面冲击所引起的传染对系统性风险的影响。本文从理论层面探讨不同的网络结构中,负面冲击是如何通过传染影响系统性风险和金融系统稳定。由于不同的网络结构中金融机构间的连接对危机的传染作用存在较大争论,本文通过分析随机网络、小世界网络和无标度网络等三种网络结构中的危机传染效应则有助于厘清这一争论。
(一)模型设定
本文首先构建一个一般的网络分析模型,然后对模型参数化,并进行数值模拟。理论模型主要基于Gai和 Kapadia模型[7](简称GK2010模型)的基本框架,并根据Battiston等[14]和Nier等[15]的研究进行扩展。由于哪一家银行第一个遭受冲击对于传染的进一步传播有着至关重要的作用,因而本文采用随机冲击和目标冲击两种冲击方式,即随机确定或有目的地选择连接最高的金融机构作为第一个遭受负面冲击的节点。
一旦银行的资本下降为0,该银行即破产,并被迫出售其资产。银行的债权人为平等对待债权人,即普通债权平等受偿,银行i违约后,每一个债权人j都能收回其对i的一部分债权,这一回收率记为ρ,由资产清算内生决定。但债权往往很难在短期内回收。因此,与Gai和Kapadia[7]一致,本文假定回收率ρ=0。为保证网络结构不存在内生演化,并保持不变,假定不对遗留在违约银行投资组合中的同业资产采取任何行动。
违约过程如下:在遭受初始冲击后,某一银行破产,并导致其债权人的资产(或资本)出现损失。如果扣除损失后,债权银行的资本不满足偿付条件,则该银行受初始破产银行的传染而破产。初始破产银行的债权银行破产又将导致其债权人资产损失,并会引起某些债权人破产。这个过程一直持续到不再出现新的破产银行为止。
(三)资本动态
银行资本(净资产)的动态决定银行是否失败,下面考察银行的资本动态。
如果没有明确说明,下文中的小写符号均表示对应的大写变量与资产价值之比。为避免出现过多的符号,以下分析将省略一些不必要的指标i和时间变量t。
三、模拟设定与结果
本文模拟随机网络、小世界网络和无标度网络三种网络拓扑结构中,原始违约通过传染引起系统性风险的结果。
(一)模拟设定
模拟不同的平均度下,初始违约通过传染所引起的破产银行数量。平均度代表了银行拥有的平均交易对手数量,它可以通过经验研究计算得到,也可以计算理论研究中节点度分布的期望值而获得。实际上,平均度等同于网络的连接度,反映了金融系统中风险分散程度,它是传染发生的主要途径。在网络不存在任何连接的极端情况下,任何机构遭受负面冲击都不会影响其他金融机构。通过改变平均度,能够得到不同连接水平下的传染频率和传染程度。传染频率(frequency of contagion)是指单一银行违约冲击引起金融系统中至少5%的金融机构失败的概率。传染程度(extent of contagion)是指传染发生(5%以上的金融机构因原始冲击而违约)的情况下,违约银行占全部银行的比率[7]。根据不同的平均度,分别重复模拟过程1 000次,计算不同平均度下的传染频率和传染程度。
模拟时,首先需要构造金融网络。假定金融网络由1 000家异质银行构成,从而生成一个由1 000个节点组成的随机网络、小世界网络(重连概率005)和无标度网络。为计算方便,假定网络中的每一条连接都是双向的,不过同一条连接不同方向的权重不同。然后,根据对数正态分布为网络中的每一条边赋权,对数正态分布的均值为152百万元,标准差为08百万元[16]。至此,银行间网络已构造完成,并确定了每个银行的同业资产和负债。其次构造每个银行的资产负债表。为确保银行总资产大于同业资产或同业负债,假定银行的总资产为maxAi(0),Li(0)=025·Ai(0),这就得到每个银行的总资产。定义资本比率为总资产的一个固定值ci(0)=c。与巴塞尔协议II对银行资本充足率的要求一致,假定c=004。资产负债表中,资产的其他部分为外部资产,负债的其他部分为存款。至此,银行的资产负债表已经构造完成。
在模拟中,假定时间离散。在0时刻,负面冲击导致一个银行出现违约,并导致其外部资产损失1/2。该银行违约将通过金融网络传染至其他银行,一旦其他银行的资本受其影响小于0,则这些银行也会出现违约。违约过程将一直持续到不会出现新一轮银行违约,即χ(t+1)=χ(t),此时,传染达到稳定状态。当违约级联终止时,计算传染程度和传染频率。最后,假定资产回收率ρ=0。
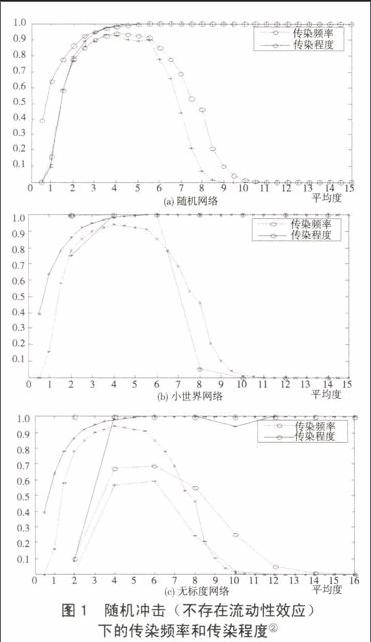
(二)基准情形:不存在流动性效应的随机冲击
模拟时首先考虑基准情形:在全部银行中以相等概率随机选择初始违约银行,并且网络中不存在流动性效应,即α=0。图1报告了基准情形的模拟结果。
图1(a)揭示随机网络中,风险分散程度对金融稳定的影响是非单调的。具体来说,当平均度较低时,传染频率和传染程度都是随着平均度的增加而增加的;而当平均度足够大时,金融网络的风险分散作用将占据上风,由此导致传染频率逐渐下降至0。因此,金融网络中的传染存在两次相变,并形成一个传染窗口:第一次相变(底部相变)发生在节点度小于1时,第二次相变(上部相变)发生在节点度为85左右,
