高频股指期现货市场多尺度波动溢出效应分析——基于集合经验模式分解和CCF检验

朱莉

(新疆财经大学金融学院，新疆乌鲁木齐830012)



高频股指期现货市场多尺度波动溢出效应分析
——基于集合经验模式分解和CCF检验

朱莉

(新疆财经大学金融学院，新疆乌鲁木齐830012)

摘要：为了防范股票市场与股指期货市场间的风险联动，两市场间波动溢出效应的研究受到了广泛关注。文章以沪深300股指期现货市场2014年10月17日—2015年1月9日内的1分钟高频数据为研究样本，选用EEMD对数据进行分解、重构，并结合CCF因果检验从三个不同的频域研究了股指期现货市场波动溢出效应。研究发现，在任何频域下股指期现货市场间的瞬时波动溢出效应显著，不同的频域不同的持续期波动溢出效应有差异，有时有双向溢出，有时只有现货对期指的单向溢出，现货市场领先时的波动率溢出更强烈，因为现货市场价格的变化领先于期货市场，所以现阶段两市场间风险联动的防范应该更多地关注股票现货市场。

关键词：高频；经验模式分解；CCF检验；波动溢出效应

一、引言

从2014年7月开始到2015年的1月，A股市场出现一轮快速的上升行情，特别是在2014年的11月股票市场突破了自2011年以来的阶段性高点，达到2600点，随后在11月21日到12月9日12个交易日涨幅达到了23%，股票市场风险陡然增加。2010年4月我国第一份股指期货合约上市，截止到2015年4月累计成交金额574.65万亿元，仅2014年总成交金额就达163.14万亿元，在全球股指期货成交额中排名第二，开户数总计23.3万户，国内期货总开户中的30%都是期指，它已经成为我国期货市场最活跃的金融工具之一。因为沪深300股指是沪深300股指期货合约的标的资产，所以为了防范股票市场与股指期货市场间的风险联动，股指期货与现货指数的波动特征及波动传递机制的研究备受学界和各类市场参与者关注。通过对两市场间波动关系的研究不仅可以深入细致地分析期指的运行效率，确定期指价格发现功能发挥的程度，以及对我国获得股票现货市场定价权起到多大作用，而且对两市场间波动关系的把握，可以帮助投资人掌握两市场间价差的变化规律，并以此为根据选定合适的投资策略获得更好的收益或者规避风险。

二、文献综述

国外学者对股指期现货市场波动溢出进行了大量研究。Chan[1]以SP500指数期现货为研究对象，选用多元GARCH模型分析了两市场间的波动传递效应，找到了证据证明波动率具有双向显著溢出效应。Antoniou和Holmes[2]以FTSE 100指数期现货为研究对象，运用GARCH族模型研究了期指推出对标的现货市场的影响，证实期指价格的变动可以较好地反应标的现货市场的信息，期指的推出增加了标的股票市场价格的波动，但是总体来看有利于市场价格的稳定。Tse[3]以DJIA期现货为研究对象，选用双变量EGARCH模型研究波动率溢出效应，研究证实信息溢出在两个市场间同时存在，期指价格变动对现货的影响要大于现货价格变动对期指的影响。Zhong等[4]以墨西哥股指期现货为研究对象，选用添加了误差修正项的VECM-EGARCH模型研究两市场间价格变动的相互关系，发现由于期指产品的推出，标的现货市场价格变动更剧烈了，但是期指可以较好地预测标的现货市场的价格。Kavussanos等[5]以希腊股票指数期现货为研究对象，利用VECM-GARCH-X模型估计了市场间的价格变动关系，发现期货市场价格的变动会影响现货市场价格的变动，但是反向的价格变动影响关系不存在。

近年来国内学者也对我国股指期现货市场进行了研究，严敏等[6]以沪深300期指仿真交易数据为研究对象，选用添加误差修正项的GARCH族模型和公共因子模型研究发现，当在一个较短的时间时，有互相的非对称波动溢出，但是在一个较长的时间时，没有互相的非对称波动溢出，在两市场价格的变化过程中，期指没有起到引领的作用。刘庆富等[7]以沪深300股指期现货为研究对象，分别从日内和隔夜信息的角度研究波动的相互影响，发现两市场间有双向的风险传递，收益具有正向杠杆效应，风险具有反向杠杆效应，一个市场前一天的信息可以对另一个市场第二天的交易价格变动产生显著的影响，而且股票市场的风险溢出大于股指期货的风险溢出，期指市场前一天的信息影响其后一天价格的变化。曹海军等[8]选用多元GARCH模型，分析不同资本净流入背景下我国股指期现货市场的风险传递及其相互影响，结果显示，价格的波动在期指市场需要更长的时间来消化，期指对现货市场的溢出效应更大一些，但是只有股票现货市场具有杠杆效应。陈创练等[9]以中国、美国、日本及香港股指期现货为研究对象，分析市场间的信息溢出效应及相关性的时变特征，研究发现：四个国家(地区)两市场间均存在双向均值、波动率溢出效应，新兴经济体两市场动态相关系数较小，而发达国家两市场动态相关系数较大。蔡庆丰等[10]构建了VECM-UJR-DCC-MUARCH-t模型，并实证分析沪深300期现货市场的动态波动关系。结果表明：沪深300期现货市场波动之间整体有较高关联性，但相关程度变化不定，在行情上涨时期两者关系大幅减弱；同时，现货市场波动对不利冲击的反应更敏感；现货市场过去意外冲击和过去波动都会抑制期货市场波动，而期货市场过去意外冲击和过去波动则会加剧现货市场波动。

综合上述，目前文献多从时域角度来研究股指期现货间的波动特征及其溢出关系，而忽视了从频域维度上来研究波动率时变特征，而且在进行溢出因果关系检验时通常都采用Granger因果检验，该方法可以较好地检验线性的影响，但是非线性是时间序列数据中常见的问题，所以一般的线性VAR模型不能够准确地、充分地描述实践中复杂数据的Granger因果检验。因此文章在以下三个方面做了一些探索：一是把EEMD引入金融高频数据的处理中。金融高频数据是非线性非稳定的数据序列，EEMD是一种适合于非线性非稳定数据处理的方法，而且分解的基函数来自于数据本身，分解后的各个分量可以更好地反应数据特性。二是从频域的角度研究股指期现货市场的波动溢出。EEMD及其重构把数据分解成短周期、中周期和趋势项，并且都各自有自己的含义。三是采用CCF波动溢出检验，该方法可以提高传统Granger因果检验的检验效率，而且可以使得波动溢出关系的检验延伸到所有滞后阶数下，反应了所有滞后阶数下波动溢出效应的总和。

所以本文运用国际上前沿的时频分析方法将沪深股指分解为高频分量、低频分量和趋势项三个部分，对其进行结构分析与比较，并采用CCF波动溢出检验研究股指期现货市场间重构分量之间的溢出关系。

三、计量方法

(一)集合经验模式分解

EMD是由Huang[11]等提出，已被广泛地用于从非线性和非平稳数据过程中提取数据信号。它认为由于数据的复杂性，可能在同一时刻共存多种不同的振动模式，EMD可以基于数据本身的特征从原始时间序列中提取本质模式，然后利用每一个本质模式作为一个本质模式函数(IMF)，该函数满足两个条件：一是该函数极值的数量和过0点的数量同样多或者最多相差一个；二是该函数是对称的，对称轴为时间轴，并且从局部来看，极值的均值为零。这两个条件保证IMF是一个近似的周期函数，平均值被设置为零。IMF是一个谐波函数，在不同的时间变量振幅和频率不同，在实践中，IMF通过一个“筛过程”提取。因为EMD进行滤波时的基函数是根据信号固有的特点来确定的，筛过程的参数都是自设定的，人的主观判断对滤波的影响降低，所以这种自适应滤波方式使得非线性和非平稳的信号在滤波后有用信号得到最大限度的保留。相对于传统的基于傅里叶分解的频谱分析，EMD的优势可简要概括如下：首先，它可以减化数据，从非平稳和非线性过程转化为简单的独立的固有模态函数。第二，EMD的分解过程是在极值用“筛”，“筛”的确定来自于数据自身的时间特征，它是局部的、自适应的、具体蕴涵和高度高效，这个特性使得EMD不同于小波分析。第三，IMF分量有一个明确的瞬时频率作为相位函数的导数，所以Hilbert变换可以被应用到IMF，允许我们能够在时间—频率—能量空间分析数据。

早期采用的EMD出现信号分量与IMF分量分类交叉的情况比较多(模式混叠)，即差异非常大的多个信号分量同时出现在一个IMF分量中，或者不同的多个IMF 分量同时包含了同一个信号分量。为了克服这个问题，Wu和Huang[12]提出了EEMD。EEMD认为每一个观察到的数据是真实的时间序列和噪声的合并，每个独立观测收集的数据都具有不同的噪声水平，高斯白噪音的一个典型特性就是频率分布均匀，当把高斯白噪音添加到含噪信号中时，含噪信号就可以转换为不同尺度上的连续信号，这一转换使得原始信号极值点的特性改变，抗混分解能力提高，很大程度上解决了模态混叠的问题。加入白噪声后的序列在一个IMF中为可比尺度的信号提出了一个在时间—频率和时间—尺度空间的统一参考框架，然后通过统计平均自行消除。它显著地降低了模式混叠的几率，并显著改善了原有的EMD。从本质上来说，EEMD就是在经验模式分解的过程中添加白噪音，基于对白噪音特性考虑，通过集合平均的方式提取数据中的真实信号，集合平均是接近真实的时间序列。

EEMD的过程如下

(1)在目标数据中添加白噪声序列。

(2)确定时间系列X′(t)中所有极值。

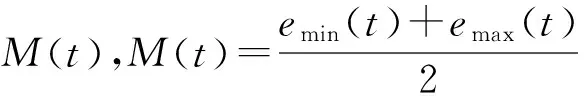
(4)从时间序列中提取出均值，分别定义X′(t)，m(t)，h(t)，h(t)=X′(t)-m(t)。

(5)检验的h(t)属性。假如它是一个IMF，记是第i个IMF，更换X′(t)的残差r(t)=X′(t)-m(t)。第i个IMF通常被记为c1(t)，假如它不是一个IMF，更换X′(t)为h(t)；重复1—5步，直到残差满足停止标准。

本文借鉴Zhang[13]提出的Fine-to-coarse重构算法的思路，首先分别计算各本征模态函数的平均值，然后用t-test依次识别各IMF均值偏离0的显著性水平，当第一个显著不等于0的分量均值出现时，那么该分量即为分界点，该分量之前的所有分量可以重构为一个高频分量，该分量表示较短时间的变化，从该分量开始直到残差分量之前的所有分量可以重构为一个低频分量，该分量表示较长时间的变化，残差项表示长期的变化，这一长期的变化即为趋势。

(二)CCF(Corss-Correlation-Function)检验

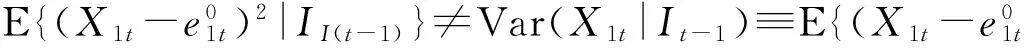
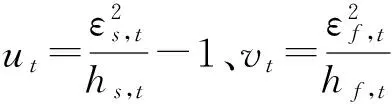
(5)

cutut(0)、cvtvt(0)分别为变量ut，vt的样本方差

cutvt(j)为ut，vt交叉协方差函数

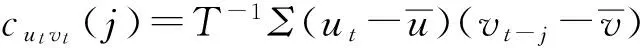
j=0，±1，±2……

(6)

四、EEMD分解-重构后不同频域的特征分析

文章选用2014年10月17日—2015年1月9日内的1分钟高频交易数据，为了构造连续数据，股指期货合约以当月主力合约为研究对象。剔除不匹配数据，每天有241对有效观测值，整个样本期59天，共有14 219对有效观测数据。

Wu和Huang[12]认为，在实际运用EEMD时，添加的白噪音的振幅可以确定为原信号标准差的倍数，集合的次数可以依据惯例设定，本文设定白噪声序列的标准偏差为0.2，集合次数为100次，IMF分量的数量为logN，N是数据序列的长度(Zhang[11])。经EEMD分解得到12个IMF分量和1个残差，接着对每个分量的均值进行t检验，检验结果显示，期指的1-9的分量不接受显著异于0的假设，从第10个分量开始，接受显著异于0的假设，即第10个分量为分界分量，则依据之前的约定，可以把1-9的9个IMF分量重构为高频分量，即短周期分量，把10-12的分量重构为低频分量，即中周期分量。标的现货的信号分解-重构的过程与期指相似，也是以第10个分量为分界点。股指期现货价格重构后的三个周期(短周期、中周期、长期)的统计特征如表1所示。从表1可以看出，收益率均值除现货高频项和期货中周期项外其余均为正值，在高频带上沪深300指数期现货尖峰后尾现象较明显，但是在低频带和趋势项上尖峰厚尾特征现象明显改善。由JB统计检验知所有周期收益率不服从正态分布的假设。从图1中也可以看出，图1a 是IMF1-IMF9重构后的高频分量，它代表了价格在较短时间的变动情况，可以看出当时间较短时价格变动较频繁且振幅较小。图1b为IMF10-IMF12重构低频部分，低频数据上每一个向上或者向下的运动是重大事件的反应，代表了重大事件的影响。图1c是残差项，表示变量变化过程的长期趋势。观察可以发现图1c中期现货的趋势项有两个交点，因为纵轴表示收益率的大小，所以交叉点前后只表示收益率的相对大小，即在第一个交叉点之前说明现货的趋势项收益率大于期货趋势项收益率，第一个交叉点到第二个交叉点之间说明现货的趋势项收益率小于期货趋势项收益率，第二个交叉点之后说明现货的趋势项收益率大于期货趋势项收益率，这说明现货对期货的影响程度较小，因为在绝大部分时间里，当现货价格上升时期货的上升幅度小于现货，当现货价格下跌时期货开始时下跌幅度小于现货，只是在后期很短的一段时间内出现期货下降幅度大于现货。进一步通过对最高点到达的先后顺序的比较可以看出，现货先到达最高点然后期货才到达，随后现货开始下降，期货在到达最高点后也开始下降，从长期来看现货价格的变化领先期货价格的变化。图1d是中周期变化与长周期变化之间的关系，可以看出，从中周期来看，价格具有明显的波动，但是从长周期来看，不论中周期的价格怎样波动，它始终围绕长周期的价格在波动，也就是说趋势项代表了未来价格的变化，长期价格由残差项的趋势来反映。

注：F-股指期货原始数据；FH-期指重构后的高频分量；FL-期指重构后的低频分量；FR-股指期货残差部分；S-股票指数原始数据；SH-股票指数高频部分；SL-股票指数低频部分；SR-股票指数残差部分

五、重构分量的波动溢出检验

利用CCF波动溢出检验，要先构建GARCH波动率模型，在构建GARCH模型前首先要进行数据的平稳性检验，所以文章对EEMD分解-重构后的三个分量分别进行了单位根检验，结果如表2所示。

根据表2可以看出，股指期现货的短周期分量与中周期分量在三种情况下的ADF检验值都显著拒绝存在单位根的假设，因此序列平稳，可以直接构建ARCH(1,1)均值模型计算标准化波动率。但是长周期分量在任何一种情况下进行ADF检验均无法拒绝存在单位根的假设，因此序列不平稳，所以进一步对两个长期分量进行协整检验，检验结果如表3所示，一阶差分存在协整关系，因此构建Vecm-bekk-garch模型来计算标准化波动率。

注：ADF检验类型(c,t,d)，其中c表示常数项，t表示线性趋势项，d表示变量差分阶数。滞后阶数根据SIC值最小化选取。

分别对股指期现货相应短周期、中周期波动分量与长期趋势分量构建CCF模型进行波动溢出的因果检验，计算样本期内均值方程20阶领先-滞后的交叉相关系数CCF，结果如表4、5、6所示。就短周期波动分量波动溢出检验而言，如表4所示，期现货市场间的瞬时相关性CCF(0)为0.627 5，即存在显著的瞬时方差因果关系，即显著的瞬时风险溢出。当现货领先期货1期时，有显著的现货到期货的波动溢出，但是期货到现货无显著溢出，而且随着领先-滞后阶数的增加期现货之间无波动溢出。这可能是因为，根据EEMD降噪的原理，数据被EEMD分解为多个IMF分量，这些IMF分量依据频率从高到低顺序排列，噪音通常较多的分布在频率较高的分量中，也就说分量中噪音的含量与分量的频率成正向关系，分量频率越高则噪音含量越多，所以对于各分量来说，由于交易成本、交易时间差异等微观市场结构误差的影响，重构后的高频分量主要反映的是噪音的波动，期现货市场噪音波动溢出效应较弱。

注：*表示0.05%的显著水平

注：**表示0.01%的置信说平下的双尾检验显著。

注：**表示0.01%的显著水平下的双尾检验显著。

就中周期分量的波动溢出检验结果来看，如表5所示，期现货市场间的瞬时相关性CCF(0)为0.174 8且显著，存在显著的瞬时收益率的波动溢出，这说明信息在期现货市场间的传递速度较快。在20阶的领先滞后检验过程中可以看出，两市场间存在显著的双向波动溢出，而且在较长的时间里均有波动溢出，随着领先滞后阶数的增加，波动溢出效应逐渐减弱。期货市场领先时的CCF值大于现货市场领先时的CCF值，说明期货市场领先时对现货市场的影响更大，检验结果也说明CCF检验对波动溢出很敏感。显著的双向波动溢出说明两市场间中期存在较为紧密的互动关系，但是相比较而言期指市场占主导地位。

就长期分量的波动溢出检验结果来看，如表6所示，期现货市场间的瞬时相关性CCF(0)为0.053 1且显著，即存在显著的瞬时收益率的波动溢出，这说明信息在期现货市场间的传递速度较快。在20阶的领先-滞后检验过程中，第5、10、11、12、16阶无显著的期货向现货的波动溢出，在第15、17阶无显著的现货向期货的波动溢出，在第14阶无任何波动溢出，其他阶数都有显著的期货向现货或者现货向期货的波动溢出，即双向波动溢出，而且波动率双向溢出效应不连续，波动率的交叉相关性随领先-滞后阶数的增加无规律变化。在前13阶和18、20阶时，现货市场领先时的CCF值大于期货市场领先时的CCF值，说明此时现货对期货的波动溢出更大，但是在14、15、16、17、19阶时期货市场领先时的CCF值大于现货市场领先时的CCF值，说明此时期货对现货的波动溢出更强烈。所以从总体上来看，现货对期货的波动率溢出效应更强烈，这些结论也反映了CCF具有较强的检验效果。

注：**表示0.01%的置信说平下的双尾检验显著。

六、结论

综合上述可以看出，股指期现货市场间的波动溢出关系不是单一的，而是随着价格内在波动周期的不同而呈现出不同的变化特征。

(1)各频域分量的瞬时相关系数分别为0.627 5、0.174 8、0.053 1，经检验波动溢出效应很显著，即表明波动率溢出现象会在两个市场间快速发生，一个市场受到信息冲击发生价格变化的同时另一个市场会立刻受到影响。

(2)在发生完瞬时波动率溢出后，短周期分量几乎再无波动溢出效应，也就是说因为微观结构噪音导致的波动溢出很快就被市场消化，不会产生持续的影响。

(3)中周期分量的波动溢出规律与短周期分量完全不同，两分量间波动互动关系强烈，且两个分量间有持续较长时间的波动溢出，这说明期现货市场间波动率溢出的影响要持续较长时间。

(4)对于趋势分量来说，不同的滞后阶数下存在不同的方差的因果关系，波动率在前4分钟有显著的双向溢出，即不论是期货领先还是现货领先，前4分钟都有波动率的溢出效应发生，但是在4分钟之后双向溢出效应不连续，期货领先时有的阶数没有显著溢出。通过比较交叉相关系数可以看出有时现货对期货的波动溢出更强烈，有时期货对现货的波动溢出更强烈，但是总体上来看，现货对期货的波动率溢出效应更强烈，这些结论也反映了CCF具有较强的检验效果。

综合上述，股指期现货市场间的瞬时波动溢出效应显著，不同的频域波动溢出效应有差异，但是总体上来看，随着领先滞后时间的延长，波动率的溢出有时有双向溢出，有时只有现货对期指的单向溢出，现货市场领先时的波动率溢出更强烈，因为从趋势项的分析知道现货市场价格的变化领先于期货市场，所以现阶段两市场间风险联动的防范应该更多地关注股票现货市场。

从理论上来看，把EEMD应用于高频金融数据的分解，并从三个频域对股指期现货市场波动溢出效应进行比较研究，是对高频波动溢出效应研究视角拓展的有益探索，而且CCF检验的引入提高了波动率溢出效应检验的敏感性，使得波动率溢出效应的分析具有更好的说服力。从实践的角度来看，投资人可以从频域的角度更好地了解在不同周期下两市场间价格的动态波动溢出关系，并据此来调整自身投资策略，进行套期保值、套利和投机。管理者则可以利用价格在不同周期下的波动溢出关系对我国股指期现货市场设计市场规则、交易机制、监管方法等市场风险管理政策方面提出相应的对策和建议，从而促使金融衍生品市场健康发展，对我国宏观经济的运行提供预警，为政府有关部门提供决策支持，防范市场间的风险联动。

参考文献

[1]Chan K, Chan K C, Karolyi A G. Intraday Volatility in the Stock Index and Stock Index Future Markets[J]. Review of Financial Studies,1991,4(4):657-684.

[2]Antonios A, Phil H. Futures Trading, Information and Spot Price Volatility: Evidence for the FTSE-100 Stock Index Futures Contract Using GARCH[J]. Journal of Banking and Finance, 1995, 19(1): 117-129.

[3]Tse Y. Price Discovery and Volatility Spillovers in the DJIA Index and the Futures Market [J]. Journal of Futures Markets, 1999, 19(8):911-930.

[4]Zhong M, Darrat A F, Otero R. Price Discovery and Volatility Spillovers in Index Future Market: Some Evidence from Mexico[J].Journal of Banking and Finance, 2004, 28(12): 3037-3054.

[5]Kavussanos M G, Visvikis I D, and Alexakis P D. The Lead-Lag Relationship Between Cash and Stock Index Futures in a New Market[J]. European Financial Management, 2008, 14(5):1007-1025.

[6]严敏,巴曙松,吴博.我国股指期货市场的价格发现与波动溢出效应[J].系统工程,2009,27(10)：32-38.

[7]刘庆富，华仁海.中国股指期货与股票现货市场之间的风险传递效应研究[J].统计研究，2011,28 (11):84-90.

[8]曹海军,朱永行.中国股指期货与股票现货市场的风险溢出和联动效应：资本流动三阶段背景的研究[J].南开经济,2012(2):67-84.

[9]陈创练，黄跃. 股指期货与现货市场溢出效应及动态关系研究——基于中、美、日、香港等市场的实证分析[J]. 宏观经济研究，2014(6):113-123.

[10]蔡庆丰，郭俊峰，陈耀辉. 沪深300期现货市场动态波动关系研究:基于VECM-GJR-DCC MGARCH-t模型的视角[J]. 管理系统学报，2015(3):209-214.

[11]Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J]. Proceedings of the Royal Society A. Mathematical. Physical and Engineering Sciences, 1998, 454(1971): 903-995.

[12]Wu Z H, Huang N E. A Study of Characteristics of White Noise Using the Empirical Model Decomposition Method[J].Proceedings of the Royal Society of London, 2004, 460(2046): 1597-1611.

[13]Zhang X, Lai K K, Wang S Y. A New Approach for Crude Oil Price Analysis Based on Empirical Mode Decomposition[J].Energy Economics, 2008, 30(3):905-918.

[14]Cheung Y, Ng W LK. A Causality-Invariance Test and Its Application to Financial Market Prices [J].Journal of Econometrics, 1996, 72(1):33-48.

[15]李红权,洪永淼,汪寿阳.我国A股市场与美股、港股的互动关系研究:基于信息溢出视角[J].经济研究.2011,(8):15-25.

责任编辑廖筠

An Analysis of Spillover Effect of the High-Frequency Stock Index Future-Spot Market’s Multi-Scale Volatility——Based on the EEMD and CCF Test

ZHU LI

(School of Finance, Xinjiang University of Finance and Economics, Urumqi 830012, China)

Key words：high frequency; empirical mode decomposition; CCF test; volatility spillover effects

Abstract：In order to prevent the risk of linkage between the stock market and stock index futures market, volatility spillover effect between the two market are concerned. Based on the 1 minute high frequency data from CSI 300 stock index future-spot market from October 17, 2014 to January 9, 2015, this paper chooses EEMD to decompose and reconstruct the data, and combining the CCF causality test, studies the future-spot market volatility spillovers from three different frequency domains. The study found that, at any frequency domain there is significantly instantaneous stock volatility spillover between the future-spot markets; as the extension of lead-lag time, there are differences volatility spillover effects in different frequency domains. Sometimes there is bidirectional volatility spillover, and sometimes there is only one-way overflow from spot to futures. The spot market volatility spillover is more intense when it leads, because the spot market price changes ahead of the futures market, so at the present stage, we should pay more attention to the stock spot market when we are trying to prevent the risk linkage between the two markets

收稿日期：2016-04-03

基金项目：国家自然科学基金项目(71261024)；新疆自治区普通高校人文社科重点研究基地社会经济统计研究中心招标课题(050315C05)；新疆财经大学校级课题(2015XYB018)。

作者简介：朱莉，女，新疆财经大学金融学院讲师，中央财经大学金融学院博士生，主要从事风险管理和信息溢出研究。

中图分类号：F830

文献标识码：A

文章编号：1005-1007(2017)07-0104-10