关于《建筑边坡工程技术规范》的讨论——圆弧滑动破坏的土质边坡锚杆加固技术力学分析

吉学亮

(贵州省毕节市七星关区国土资源局，贵州 毕节 551700)



关于《建筑边坡工程技术规范》的讨论
——圆弧滑动破坏的土质边坡锚杆加固技术力学分析

吉学亮

(贵州省毕节市七星关区国土资源局，贵州 毕节 551700)

摘要：从Bishop法的基本理论及假设出发，推导边坡规范附录A.0.1圆弧滑动破坏边坡稳定性计算公式，并进一步对圆弧滑动破坏土质边坡安全系数的概念进行延伸，提出了边坡广义安全系数为总抗滑力与总下滑力之比，在边坡支护工程设计时，提出了支护工程抗力的求解方法，通过工程实例计算出边坡支护工程抗力，最后按照规范要求进行锚杆设计计算。

关键词：Bishop法；土质边坡；圆弧滑动；安全系数；锚杆

锚杆自20世纪初问世以来其以结构简单、施工方便、成本低廉和工程适应性强等特点在土木工程中得到广泛应用，在边坡支护工程中的应用更是广泛。一般情况下，对于发生平面滑动破坏的边坡，只要知道支护工程须提供的抗力，如剩余下滑力、岩土体侧向压力等就可以适宜性的采用锚杆对边坡进行支护[1-2]。易于发生圆弧滑动破坏的土质边坡，在确定了土体内部最不利圆弧形滑面后，按照《建筑边坡工程技术规范(以下简称规范)》(GB50330-3013)附录A.0.1对边坡稳定性计算，即便确定了边坡工程安全系数，也不能直接求出边坡支护工程须提供的抗力，采用锚杆对边坡进行加固时就不能确定锚杆轴向拉力等关键性设计技术参数。

关于边坡的研究，赵尚毅等用有限元强度折减法求边坡稳定安全系数，得出此方法求得的边坡稳定安全系数与传统方法的计算结果十分接近的结论[3]；雷远见利用离散元的强度折减法分析岩质边坡稳定性，验证了此种方法的可靠、有效性[4]。蒋勇军从地形地貌、岩土体性质、人类工程活动等方面探讨了重庆市地质灾害的形成机理，并从工程措施和非工程措施两方面提出了防灾、减灾对策[5]。许强对现行的直立切破及其稳定性进行了分析，根据库仑土压力理论计算推力的不合理性，并提出了相应的改进办法[6]。总的来说，关于边坡稳定性及其加固的研究较少，缺乏“圆弧滑动破坏的土质边坡锚杆加固技术力学”结合《建筑边坡工程技术规范》的分析。因此，本文以简化Bishop圆弧滑动法为基本理论，在边坡稳定性计算的基础之上，探讨圆弧滑动破坏土质边坡锚杆加固的相关力学分析及锚杆设计计算问题；旨在为地质灾害防止工作提供一定的参考。

1规范计算公式的推导

(1)简化Bishop基本假设。①满足整体力矩平衡及静力平衡；②满足各条块垂直方向静力平衡，不满足各条块力矩平衡条件；③考虑条块间的作用力，但只考虑垂直于条块分界面的法向力，切向力为零；④假设各条块的安全系数与整个圆弧滑动面的安全系数相同；⑤定义安全系数的概念为圆弧滑面土体抗剪强度与实际剪应力之比。

(2)规范公式的推导[7]。如图1所示，第i块土条受到的非水平力，包括重力Gi、竖向荷载Gbi、条块底部法向力Ni、条块底部切向力Ti以及单宽水压力Ui，设该条块底部圆弧长度为li，弧线中点圆弧切线与水平方向夹角为θi，土的粘聚力为c，内摩擦角为φ，该滑块安全系数为Fs。

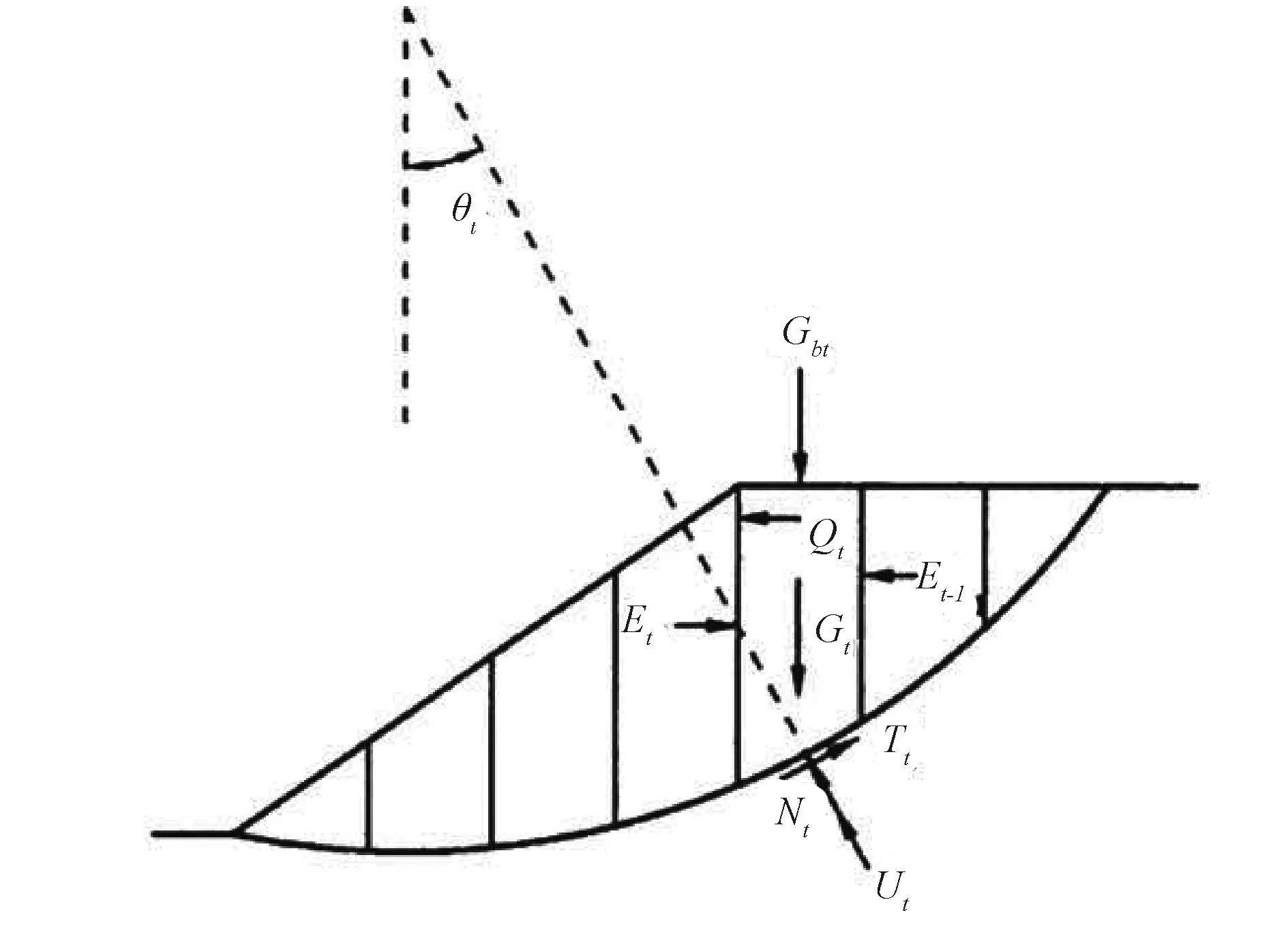
图1　圆弧滑动法边坡计算示意

根据简化Bishop安全系数的定义则有：

(1)

式中：分子分母分别为边坡土体的抗剪强度和实际剪应力，根据摩尔-库伦准则和有效应力原理，条块底部土体的抗剪强度为：

τf=c+(σi-ui)tanφ

(2)

式中：σi为最大主应力，ui为孔隙水压力，则由公式(1)～(2)可得出条块底切向力：

(3)

根据简化Bishop法基本假设，垂直方向静力平衡，对于图1中的第i块土条则有：

Nicosθi=Gi+Gbi-Tisinθi

(4)

将公式(3)代入公式(4)，则可以得出条块底部法向力为：

(5)

(6)

根据简化Bishop法基本假设，所有条块整体满足力矩平衡，由于条块间作用力Ei、Ei-1总是成对出现，大小相等，方向相反，故条块间的力以圆心取矩时相互抵消，只有Gi、Gbi及Ti对圆心取矩形成力矩平衡，即：

(7)

由公式(6)可知：

(8)

将公式(8)代入公式(5)，又可得到条块底部法向力的另一种表达方式：

将寿命因数fh=1.693、力矩载荷因数fm=1、冲击载荷因数fd=1.5、速度因数fn=1.569、温度因数fT=1代入式(6)，即得当量动载荷P=67.8 kN.

(9)

将公式(9)代入公式(3)，进行下列推导计算：

将以上推导得出的关于Ti的表达式代入公式(7)，容易得出Fs的迭代计算表达式，详见公式(10)，这就是简化Bishop法圆滑滑动土质边坡的稳定性计算公式。

(10)

公式(10)中，若每个条块的c、φ值各不相同，且考虑水平荷载，那么上式的表达形式即与规范中附录A.0.1相关公式相同。

2锚杆加固力学分析

在简化Bishop法的基本假定中，虽然定义了边坡安全系数的概念是滑面土体抗剪强度与实际剪应力之比，然而通过公式(10)我们发现，公式中的分子是圆弧滑面土体能承受的最大剪力，或称之为总抗滑力，而分母则是各条块沿圆弧下滑力之和。那么边坡稳定性系数也可广义的理解为沿圆弧滑面上的总抗滑力与总下滑力之比，即：

(11)

然而与平面滑动破坏边坡不同的是，圆弧滑动边坡的总抗滑力是在进行多次迭代计算，得出最不利圆弧滑面上边坡安全系数之后，才能确定总抗滑力，而平面滑动破坏的土质边坡，只要知道滑动面的位置及形状，就可以先计算抗滑力和下滑力，然后得出边坡的安全系数。

工程应用中，在计算土质边坡稳定性时，公式(11)基本无指导义，大多是利用计算机技术确定最不利圆弧滑面的位置迭代计算得出边坡安全系数。但是在进行边坡支护工程的设计计算时，公式(11)就成为关键性依据，假设边坡支护工程设防安全系数为Fst，边坡支护工程延米提供抗力为F，那么就有公式(12)：

F≥Fst总下滑力-抗滑力

(12)

如图2所示，高度为H的边坡坡面上共布置n列锚杆，同列第i根锚杆轴向拉力设计值为Ni，锚杆水平间距为d，锚杆轴向与破裂面法线方向夹角为αi，设公式(10)中的分子、分母分别为A、B，支护工

程延米提供抗力为F，则有：

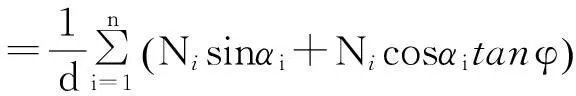
≥FstB-A

(13)

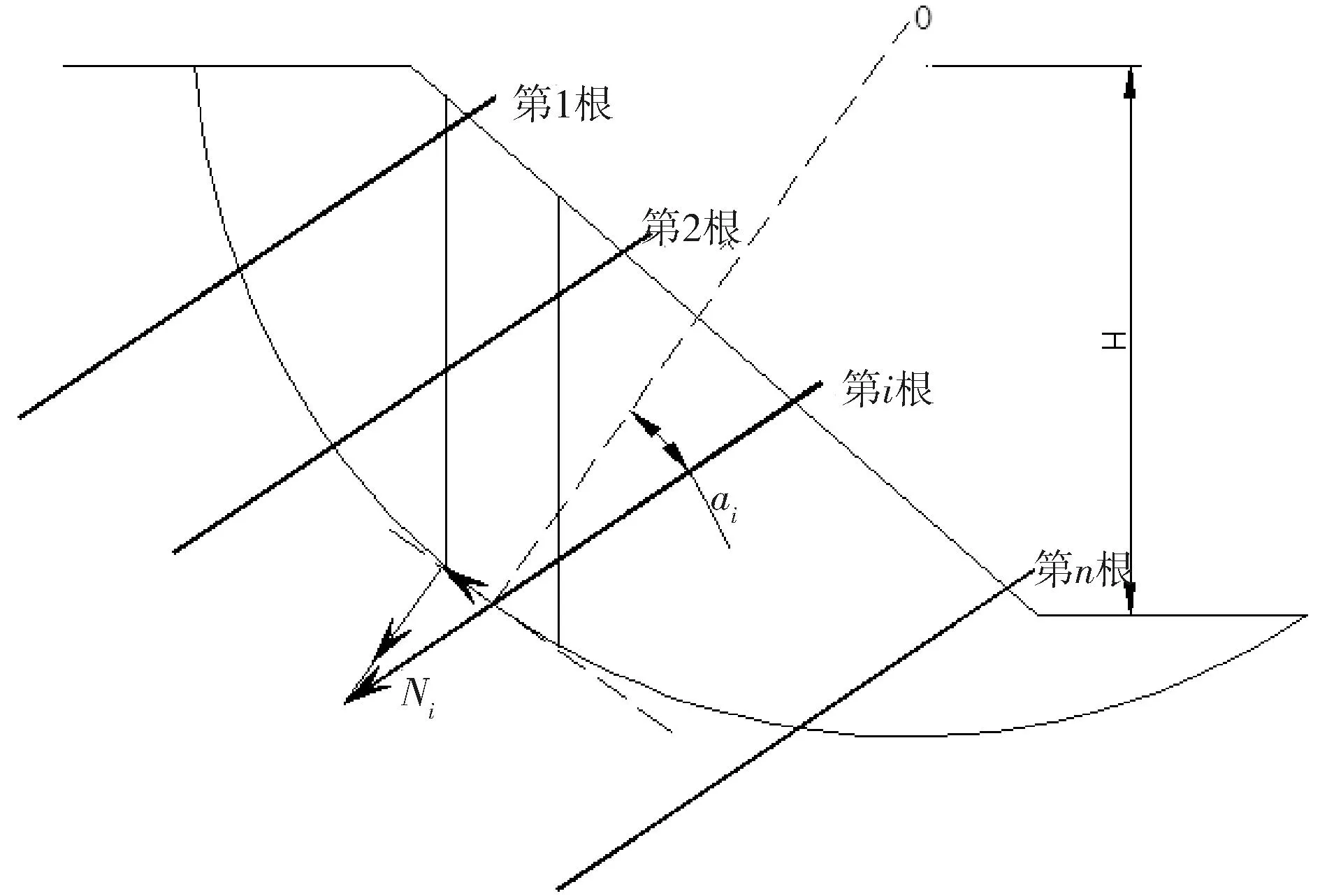
图2　边坡锚杆加固力学分析示意

3工程案例

贵州遵义某地有一高度15m的临时性土质边坡，安全等级为二级，坡顶水平且无荷载作用，坡面斜率1∶0.5，边坡土体内摩擦角15°，粘聚力35kPa，呈硬塑状，支护工程不考虑水的影响，试对该边坡采用锚杆进行支护设计。

按照简化Bishop法进行计算，采用计算机技术自动搜索出最危险滑面，采用公式(10)进行人工迭代计算(表1)

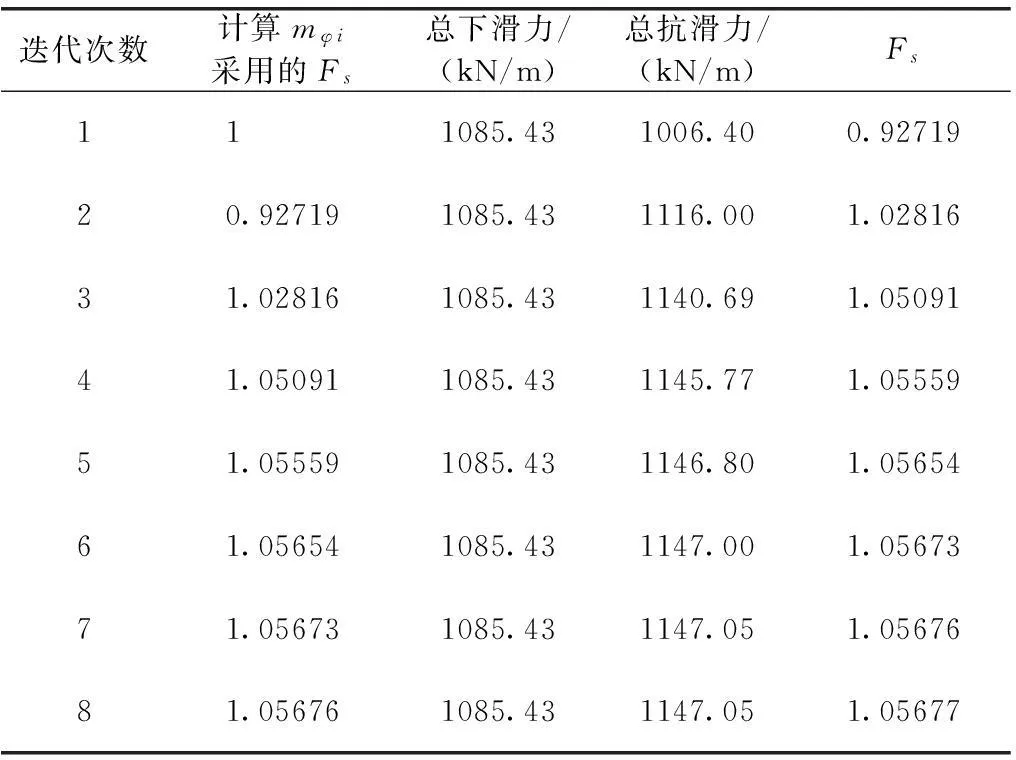
表1　边坡稳定性迭代计算

取临时性二级边坡工程安全系数1.2，根据公式(13)，边坡沿最不利圆弧滑面上的抗滑力、下滑力等数据取表1中第8次计算的数据，容易计算得知边坡支护工程抗力最小值为155.46.0kN/m。锚杆加固工程设计主要按照下列步骤进行。

(1)确定锚杆轴向拉力。假设锚杆纵横间距均为3m，则同一列锚杆可按照5根设计，入射角30°，每根锚杆轴向拉力值相同，均为Nak，根据公式(13)则有：

≥Fs tB-A=155.46kN

(14)

从高处边坡底部1.5m的位置开始布置锚杆，则各列锚杆的αi及其正、余弦值见表2。

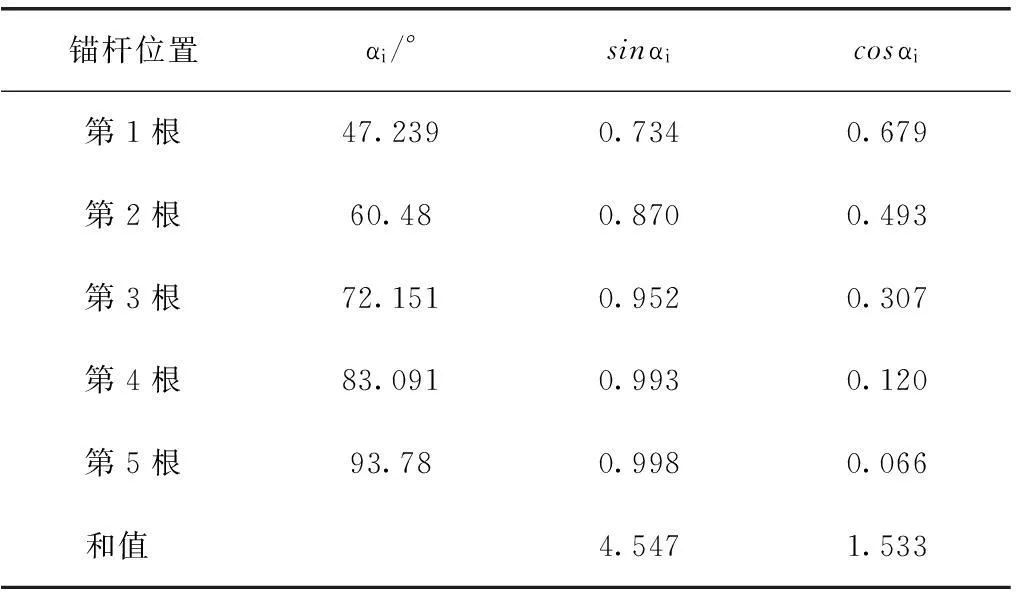
表2　边坡稳定性迭代计算

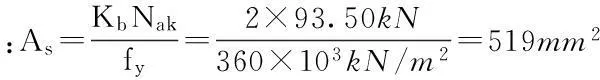
(3)确定锚固段长度规范中锚固段长度的计算公式有8.2.3和8.2.4两个，但实际土层锚杆锚固段长度均系由规范公式8.2.3确定，取锚固体抗拔安全系数1.8，锚孔直径0.2m，土与锚固体极限粘结强度标准值取100kPa，则锚固段长度计算如下：

实际设计锚固段长度3.0m，那么锚杆抗拔能力主要由锚固段长度确定，根据设计锚固段长度计算锚杆抗拔力为：

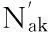
将上式计算值代入公式(14)中进行验算：

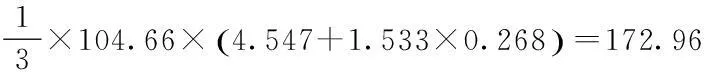
4存在的问题及思考

在用锚杆对土质边坡进行加固时，锚杆的轴向力最终分界为沿最不利圆弧的抗滑力，或者说锚杆轴向拉力增加了最不利圆弧能承受的最大剪力。由公式(13)及公式(14)可知，Naksinαi是直接增加滑面抗滑力，Nakcosαitanφ是通过法向力来增加滑面抗滑力，由于土的变形多属于塑性变形，故实际上通过法向力来增加滑面抗滑力的效果是非常有限的。在有些工程资料或软件中，有人引入了法向力发挥系数的概念，一般该系数范围值是0～1，笔者建议若滑动面以上岩土体变形以弹性变形为主，那么法向力发挥系数可取1，如果滑动面以上岩土体变形以塑性变形为主，则可不考虑法向力造成的滑面抗滑力的增加，对于一般土质边坡建议取该系数的值在0.5以内。

参考文献：

[1]中华人民共和国住房和城乡建设部.建筑边坡工程技术规范(GB 50330-2013)[S].北京：中国建筑工业出版社，2013.

[2]中华人民共和国住房和城乡建设部.混凝土结构设计规范(GB 50010-2010)[S].北京：中国建筑工业出版社，2010.

[3]赵尚毅，郑颖人，时卫民，等.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报，2002，24(3)：343-346.

[4]雷远见，王水林.基于离散元的强度折减法分析岩质边坡稳定性[J].岩土力学，2006，27(10)：1694-1698.

[5]郭映忠.重庆地质灾害研究与防治[J].中国地质灾害与防治学报，1995，6(3)：1-8.

[6]许强，黄润秋.重庆市建筑开挖边坡稳定性评价及支护措施探讨[J].成都理工学院学报，1996，23(1)：32-38.

[7]高大钊，袁聚云.土质学与土力学[M].北京：人民交通出版社，2001.

Discussion on the Code for Building Slope Engineering Technology： Analysis of Soil Slope Anchor Reinforcement Technology Mechanics of Circular Arc Sliding Failure

JI Xue-liang

(Qixingguan land and resources in Bijie City of Guizhou Province ,Bijie 551700，China)

Abstract:Starting from the basic theory and the assumption of Bishop Method in this paper,calculation formula of slope was derived in specification appendix a.0.1 circular sliding slope stability.Further,the soil slope security coefficient was extended on damage to circular sliding.And the genera slope safety factor for the decline in total anti-sliding force and total force was put forward.The solution to supporting engineering resistance was put forward for the design of the slope support engineering.The slope support engineering resistance was calculated by engineering examples,and finally,it was implemented in accordance with the specification requirements anchor design and calculation.

Key words:Bishop Method;soil slopes;circular sliding;security coefficient;rock bolt

doi:10.3969/j.issn.1009-4210.2016.03.016

收稿日期：2015-03-17

作者简介：吉学亮(1982—)，助理工程师，从事地质灾害防治工作。E-mail：114608501@qq.com

中图分类号：TU457

文献标志码：A

文章编号：1009-4210-(2016)03-114-05