数学解题的认识与实践(中)
2016-07-07罗增儒
罗增儒
数学解题的认识与实践(中)
罗增儒

2.数学解题过程的操作
什么是解题过程?解题过程不仅包括书写表达,还包括从拿到题目到完全解出的所有环节或每一个步骤。通过回顾自己的实际操作(看题、想题、答题、回题)可以看到,解题通常有四个基本的阶段:理解题意、思路探求、书写表达、回顾反思。我们对这个看题、想题、答题、回题的感性过程并不陌生,问题在于能不能上升到理性的高度。比如:
我们都知道解题的首要前提是审题,但审题“审什么、怎么审”,能够说清楚、讲明白、做到位吗?
我们都知道解题的思维核心是思路探求,但思路探求“探什么、怎么探”,能够说清楚、讲明白、做到位吗?
我们都知道解题的最终呈现是书写,但书写“写什么、怎么写”,能够说清楚、讲明白、做到位吗?
我们都知道学会解题的好途径是反思,但反思“思什么、怎么思”,能够说清楚、讲明白、做到位吗?
2-1理解题意
(1)理解题意的基本含义
理解题意也叫做审题,主要是弄清题目已经告诉了你什么,又需要你去做什么,从题目本身获取怎样解这道题的逻辑起点、推理目标以及沟通起点与目标之间联系的更多信息。
题目本身是解决这道题的钥匙。只不过其中的积极提示往往是通过语言文字、公式符号以及它们之间的联系间接地告诉我们。所以,审题一定要逐字逐句看清楚,力求从语法结构、逻辑关系、数学含义、答题形式、数据要求等方面真正看懂题意。
成在审题,败在审题。弄清题意等于解决了问题的一半。解题中出现的会而不对、对而不全的情况,究其原因,多在于未审清或审不清题意。审题要抓好“审什么”的三个要点和“怎么审”的四个步骤。
(2)审题审什么。
抓好审题“审什么”的三个要点。
①弄清题目的条件是什么,一共有几个,其数学含义如何。
条件包括明显写出的和隐蔽地给予的,弄清条件就是要把它们都尽量找出来;更重要的是弄清条件的数学含义,即看清楚条件所表达的到底是哪些数学概念、哪些数学关系。有时,还要排除无关信息与干扰信息。
题目的条件告诉我们从何处下手、预示“可知”并启发解题手段,弄清了条件就等于弄清了行动的起点,也准备好了行进中的加油站。
②弄清题目的结论是什么,一共有几个,其数学含义如何。
题目的结论有的是明显给出的,如求证题,关键是要弄清结论到底与哪些数学关系、哪些数学概念有关;有的是要我们去寻找的,如求解题、探索题等。这时的弄清结论,就是要弄清求解的探索性质或探索范围,它们与哪些数学关系、哪些数学概念有关,以明确推理或演算的方向。
题目的结论告诉我们向何方前进、预告“需知”并引导解题方向。弄清了结论就等于弄清了行动的目标,也随身带上了纠正偏差的“指南针”。
③弄清题目的条件和结论有哪些数学联系,是一种什么样的结构。
在弄清条件的数学含义、结论的数学含义的基础上,继续弄清条件知识与结论知识之间存在哪些初步的数学联系,这些初步联系就表现为题目的结构(题型)。
为了更接近问题的深层结构,审题不仅开始于解题工作的第一步,还贯穿于探求的过程与结果的反思,应该是一个循环往复、不断深化的过程。
题目的条件和结论是怎样解这道题的两个信息源,审题的实质是从题目本身去获取从何处下手、向何方前进的信息与启示。
(3)审题怎么审。
抓好审题“怎么审”的四个步骤。
①读题——弄清字面含义。
首先要逐字逐句逐段地读懂题目说了什么,按每分钟阅读300~400个印刷符号的速度计算,通常读完一道题用不了1分钟,但未必读懂了。因而,还应该从语法结构、逻辑关系上作出分析,真正弄清哪些是条件,哪些是结论,各有几个,这是读题最实质性的工作。
其次要从题型特点、答题形式、数据要求上明确题目的技术性细节。比如在考试中,有的题目要求保留几位小数等。如果不按这些要求来,解答就会被认为不完整(存在扣分的危险),即使有的同学并非不会做。
②理解——弄清数学含义。
看懂题目的字面含义还不能算真正审清题意,它只是为实质性的数学理解扫清了语言障碍,关键是要能进行文字语言、符号语言、形象语言、表格语言之间的转化,从题目的叙述中获取数学符号信息,从题目的图形中获取数学形象信息,弄清题目的数学含义。这当中,我们常常要回到定义,激活相关的数学知识,还要辅以图形或记号,使条件和结论都数学化,并被我们所理解。比如:
题目的条件(或结论)说了抛物线,抛物线能加吗?能减吗?能乘吗?能除吗?能运算吗?能推理吗?有困难!所以,立即想抛物线的定义,想抛物线的表达式(符号语言)和图像(形象语言),初中的表达式是y=ax2+bx+c(a≠0),图像是一条类似抛体运动路径的曲线。一旦写出抛物线的表达式y=ax2+bx+c(a≠0)就等于设出了5个字母和它们之间的等量关系,有助于运算或推理的展开。
题目出现了正方形ABCD,但正方形能加吗?能减吗?好运算、易推理吗?应该把正方形的定义和相关性质都写出来。如∠ABC=∠BCD=∠CDA=∠DAC= 90°,AB=BC=CD=DA等,这有助于运算或推理的展开。
题目的条件(或结论)说了“二次方程有实根”,它的数学含义是什么?可以是等式,存在x0使ax02+bx0+c=0,也可以是不等式b2-4ac≥0,还可以从知识链上展开:
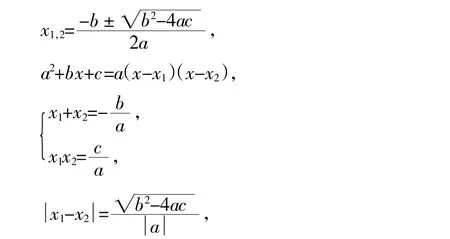
……
③表征——识别题目类型。
信息在大脑的呈现叫做表征。弄清条件、弄清结论的同时,条件与结论之间的关系会在头脑中呈现,这种呈现不仅会激活相关的数学知识,也会调动相应的解题经验。对于大量的常规题来说,条件与结论之间的关系结构是记忆储存中现成的——每人的头脑里都或多或少、或优或劣地储存有基本模式与经典题型。题意弄清楚了,题型就得以识别,提取该题型的相应方法即可解决(叫做模式识别)。即使是新的陌生情景,我们也有了解决它的逻辑起点与推理目标,继而可以用差异分析、以退求进、区分情况、层次解决、正难则反、数形结合等措施进入下一阶段——思路探求。
④深化——接近深层结构。
简单题一旦弄清了题意,题型就得以识别,思路随之打通,但有时认识是浅层的。对于变通过的、形似而质异的或综合性较强的题目,则还要不停顿地弄清问题。因而,弄清题意的工作在识别题目类型之后还结束不了,主要表现在两个方面:其一是在思路探求中,还有一个继续弄清题意的过程,否则会使思路受阻、思维走偏;其二是在思路已打通、解法初步得出时,仍有一个回顾反思、再认识的过程,即更本质地弄清问题,努力接近问题的深层结构。
经验表明,凡是题目未明显写出的,一定是隐蔽地给予的。只有细致地审题,才能从题目本身获得尽可能多的信息,这一步不要怕慢。注意:这些要点,叙述时是分解动作,真正解题时是连续进行、一气呵成的。请思考下面题目中条件是什么,结论是什么。
例1已知mn≠0,n2+4m>0,又a≠b且

试求过点A(a,a2),B(b,b2)的一次函数解析式(用含m,n的式子表示)。
讲解:条件是什么?结论是什么?
理解1:给出关于四个字母m,n,a,b的五个条件(三个不等关系、两个同形等式),mn≠0,n2+4m>0,a≠b,ma2+na-1=0,mb2+nb-1=0。
结论是求过两点A(a,a2),B(b,b2)的一次函数解析式(用含m,n的式子表示),或者说是求y=kx+h中的两个字母k,h。
理解2:关于四个字母m,n,a,b的三个条件:
条件1:给出四个字母m,n,a,b。
条件2:字母m,n满足两个关系mn≠0,n2+4m>0。
条件3:字母a,b满足三个关系:a≠b,a,b是二次方程mx2+nx-1=0的两个实根,组成两个点A(a,a2),B(b,b2)。
结论是求过两点A(a,a2),B(b,b2)的一次函数解析式(用含m,n的式子表示),或者说是求y=kx+h中的两个字母k,h。
对于题目的多个条件,先用哪个后用哪个,哪个条件与哪个条件相配合等需作通盘考虑。一个比较麻烦的想法是从已知两等式中解出a,b,再由A,B的坐标求一次函数解析式y=kx+h。另一种较为自然的解法是用待定系数法求k,h。
解法1:由①、②可解得
由于a≠b,所以A,B的坐标恰好为一个取正(负)号、另一个取负(正)号:

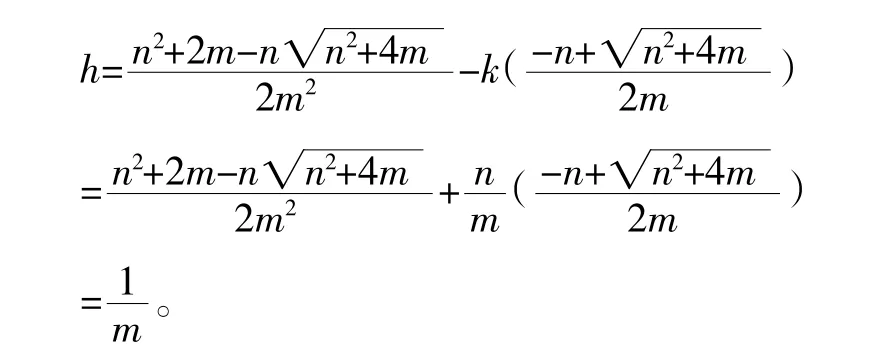
反思1:这个解法的运算能力值得敬佩,但十分麻烦,需要简化。首先,分别求出A,B的坐标a1,2,b1,2又讨论合并,有思维回路;其次,求出A,B的坐标又在解方程中消去也是一个思维回路,应该考虑这些回路是必要的还是多余的;再次,理解求k,h的方程,其实是,由相减,可得,从而h=a2-ka=a2-(a+b)a=-ab。
抓住这个实质步骤,立即可以将k,h表示为a,b之和、之积,然后将a,b之和、之积用含有m,n的代数式表示。由两数之和与两数之积很容易想到韦达定理。
解法2:设过A,B的一次函数解析式为y=kx+h,由于A,B在抛物线y=x2上,消去y,得a,b是二次方程

的两个实根,由根与系数的关系,有

但由已知两等式知,a,b是二次方程

的两个实根,又有

反思2:在解法2中,③式与⑤式都是以a,b为根的一元二次方程,④式与⑥式都有两根之和、两根之积(a+b,ab),我们有理由怀疑这里面有重复。重新理解条件与结论,a,b是二次方程③x2-kx-h=0的根表明

作为目标,需要确定k,h。而条件有①、②式成立,将其与⑦、⑧式比较,从中可以看到,二次项的系数不相同,消除差异,有0,(a≠b)。
解法3:由①,②有
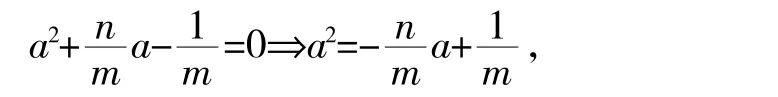

由a≠b表明,两点A(a,a2),B(b,b2)均在直线上,由两点确定一条直线知,这就是过点A,B的一次函数解析式。
评析:这个解法变解法1的运算为推理,把k,h作为整体而同时确定,把解法2中③式与⑤式的重复、④式与⑥式的重复都消除了。关键在于,运用函数与方程的思想揭示了题目的本质:已知A,B两点均在直线my+nx-1=0(mn≠0)上,变形,这就是过A,B两点的一次函数解析式。这样一来,题目几乎不用做就有答案(只要明白一次函数的图像是直线)。这就是对题意的更接近深层结构的理解:
理解3:两个字母a,b满足两个条件:
条件1:字母a,b(a≠b)组成两个点A(a,a2),B(b,b2)。
条件2:这两个点A(a,a2),B(b,b2)在直线my+ nx-1=0上(满足两个同形等式ma2+na-1=0,mb2+ nb-1=0),其中mn≠0(有了a≠b,n2+4m>0成为多余的)。
结论是求过两点A(a,a2),B(b,b2)的一次函数解析式(用含m,n的式子表示)。
(待续)
